钢衬钢筋混凝土管道开裂机理及模拟技术研究

马 铢，伍鹤皋，石长征

钢衬钢筋混凝土管道开裂机理及模拟技术研究

马 铢，伍鹤皋，石长征

(武汉大学水资源与水电工程科学国家重点实验室，武汉 430072)

钢衬钢筋混凝土管道在设计上允许外包混凝土开裂，确定其裂缝发展规律和结构的承载特性是评估管道能否长期安全稳定运行的前提，但现有的解析公式多是半理论半经验公式，不同的公式计算结果误差较大，有限元法成为了主要的分析方法．以往的有限元模型多基于损伤或者断裂理论，较少考虑二者的耦合作用，本文结合三峡水电站大比尺试验模型，建立了基于黏聚裂缝模型的有限元模型，在管道混凝土中插入内聚单元综合模拟了混凝土开裂过程中的损伤和断裂特性，得到了管道结构开裂前后的钢材应力变化规律、裂缝扩展形态以及裂缝宽度，进一步系统地讨论了内聚参数和网格尺寸的影响．有限元模拟裂缝扩展形态与模型试验时裂缝宽度中间宽、两侧较小的结论一致．管腰和管顶典型部位的裂缝宽度值与模型试验误差在10%以内，且钢材应力起伏与裂缝位置相呼应．更改内聚参数和网格尺寸发现，在合理的取值范围内，混凝土裂缝扩展、钢材承载规律与试验结果基本一致，但内聚刚度取值过小会导致混凝土开裂提前，黏结系数取值过大或者单元尺寸过大会使计算结果的精度降低．因此在采用黏聚裂缝模型模拟管道混凝土开裂时，应在保证计算收敛的前提下，尽可能取较小的黏结系数和足够大的内聚刚度，以提高计算结果的精度．

钢衬钢筋混凝土管道；数值模拟；黏聚裂缝模型；裂缝扩展；裂缝宽度；承载特性

钢衬钢筋混凝土管道是钢衬与外包钢筋混凝土联合承载的组合结构[1]，其广泛应用于大HD值(水头与直径的乘积)水电站压力管道中，在设计荷载下允许外包混凝土开裂，但裂缝宽度过大会造成钢筋锈蚀，缩短管道的使用寿命，并且开裂后应力重分布会影响管道结构的承载力，因此确定管道裂缝宽度和承载特性是评估其安全性及耐久性的重要前提．

多年来，不少学者对管道开裂前后的钢材应力分布、裂缝扩展规律及裂缝宽度计算进行了一系列的研究，主要有解析法、模型试验和数值分析法．20世纪90年代国内许多科研部门和高校进行了多个结构模型试验[2-4]，在结构承载特性、开裂特征方面获得了大量研究成果，也为管道的材料非线性数值模拟提供了丰富的验证资料，但是模型试验成本高，影响因素多，试验周期长，且模型比尺的选择对试验结果的影响很大，因此应用越来越少．蒋锁红[5]根据“单轴对称”原理，将管道结构计算模型简化为变截面固端超静定拱的杆系结构，用结构力学弹性中心法求解管道开裂前后的应力，但是管道属于厚壁结构，将管道简化为杆系结构计算结果时，在塑性阶段与原型观测结果误差较大．董哲仁等[6-7]采用正交各向异性多层环法，根据管道的环向变形，扣除混凝土极限变形，推导出管道的裂缝宽度数学模型；王康平等[8-9]根据钢筋沿弧长的应力分布提出了管道裂缝宽度计算的公式．但上述研究推导的公式都是半解析半经验的，在影响裂缝宽度的主要因素及这些因素对裂缝宽度的影响程度上均未达成一致，代入相同计算条件后得到的计算结果相差较大．

由于采用模型试验和解析法对管道开裂特征研究具有一定的困难性，随着计算机技术的迅速发展，数值分析方法逐渐成为主要的结构分析手段．伍鹤皋等[10]利用ANSYS有限元软件对三峡大比尺试验模型进行了有限元分析，得到了管道开裂前后的应力、初裂荷载以及裂缝宽度值，有限元结果与模型试验结果接近，但是在分析过程中裂缝采用分离裂缝模型，需要不断地修改网格，计算效率低．石长征等[11]、苏凯等[12]采用ABAQUS有限元软件对管道进行了平面非线性有限元计算，表明有限元结果可以很好地反映管道结构裂缝开展、钢衬和钢筋应力分布规律．裂缝采用弥散裂缝模型，虽然通过管道损伤带可以模拟混凝土随机开裂部位，但是无法获得裂缝的形态和宽度，且上述研究多是基于损伤理论或者断裂理论[13]，而考虑二者耦合作用的研究较少．管道混凝土在开裂过程中裂纹端部虽然没有塑性区，但是有较大的微裂纹区，同时存在着损伤(分布缺陷)和裂纹(奇异缺陷)[14]，因此同时考虑混凝土的损伤和断裂更符合实际开裂情况．基于内聚理论的黏聚裂缝模型(简称CCM)综合考虑了准脆性材料的损伤和断裂特性，已在复合材料的分层失效中得到广泛应用[15-16]．该模型避免了传统有限元模拟时的网格重剖难题，可以模拟混凝土结构的随机开裂过程．

本文基于三峡水电站斜直段管道结构模型试验，建立了相关有限元模型，并引入黏聚裂缝模型，在管道混凝土中插入内聚单元模拟混凝土的损伤和断裂特性，分析得到了管道开裂前后的应力分布规律、裂缝扩展形态和裂缝宽度的大小，并将数值计算结果与模型试验进行对比分析，同时进一步探究了内聚参数取值和网格尺寸对管道结构开裂的影响．

1 黏聚裂缝模型

1.1 理论模型

Dugdale[17]和Barenblatt等[18]在研究塑性和脆性材料的断裂时，发现裂纹尖端变形区为一扁平带状的内聚区域，如图1所示，由此提出了基于弹塑性断裂力学的内聚理论，该理论介于损伤力学和断裂力学之间，用于描述材料界面分离时的不连续断裂过程．黏聚裂缝模型(CCM)基于内聚理论，将裂纹分为两部分[19]：裂纹表面不受应力作用的断裂区和裂纹表面作用有应力的内聚区域，如图2所示．前者是真实的物理裂缝，表征宏观裂缝，裂缝面上不传递任何应力；而后者将带状微裂区简化为一条分离裂缝，即虚拟裂纹，虚拟裂纹面上可以传递应力，其上某点应力的大小与该点微裂面的张开位移之间存在着某种关系，称为牵引分离定律[20]，其表达式为

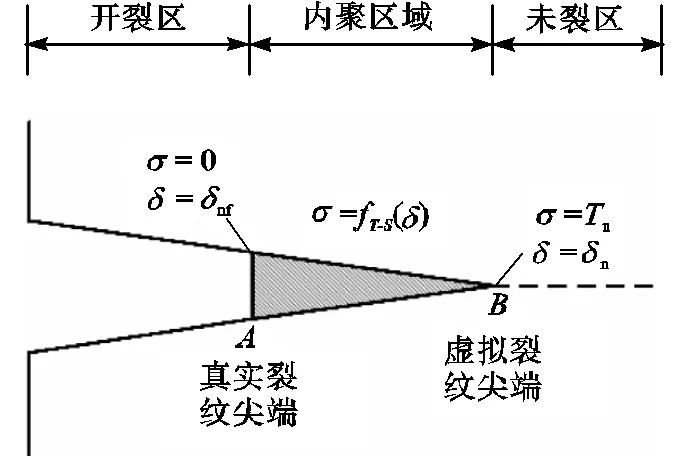
图2 黏聚裂缝模型示意

内聚区域的力学属性表现如下：在荷载作用下将首先经历线弹性阶段，当单元的受力满足起裂准则后，单元将由线弹性阶段过渡至损伤演化阶段，直至单元完全断裂失效，进而将连续介质过渡为非连续介质，由此模拟材料开裂所导致的位移非连续特征[21]．

上述过程由牵引-分离定律来描述，根据材料的不同，常用的牵引-分离曲线有双线性、梯形、多项式以及指数型[22]．混凝土常见的开裂模式主要有张开型、滑移型和撕裂型[23]，而管道在内水压力等荷载作用下主要发生由拉伸造成的张开断裂，因此本文仅考虑单元法向上的拉伸断裂．

大量试验研究[24]表明，采用双线型模型计算效率高，且适用于描述混凝土这种准脆性材料的开裂，因此本文选用双线型模型来模拟混凝土界面的开裂行为，如图3所示，其内聚本构的控制方程为

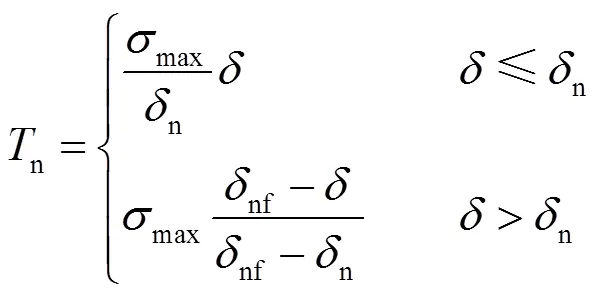
(3)

1.2 有限元模型

CCM应用于有限元计算时主要有两种实现形式：一种是在常规的接触中加入内聚接触属性，另一种是嵌入内聚单元．研究表明[25]，内嵌零厚度的内聚单元模拟混凝土等准脆性材料开裂的效果最好，因此本文采用内嵌零厚度的内聚单元模拟管道的开裂过程，图4和图5分别为ABAQUS中常用的二维和三维内聚单元．

在外力作用下，内聚单元的上下两层节点将沿着单元厚度的方向发生相对移动，通过正应力和两个切应力反映断裂过程中的骨料咬合、摩擦以及黏结效应．内聚区域的单元数目过少时，裂纹尖端的扩展不能得到准确的模拟，因此内聚区域的单元划分要求十分精细，网格尺寸要小于内聚区域的长度．通用的求解内聚区域的长度计算式[26]为

图5 ABAQUS中三维内聚单元COH3D8P

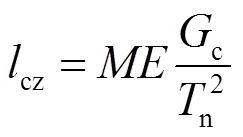
式中：为混凝土的弹性模量；c为临界断裂能；n为最大内聚力强度；为与内聚区域模型选取相关的系数，通常取为1．

内聚刚度在理论上等于混凝土的弹性模量除以内聚界面的厚度，通常情况下内聚界面都非常薄甚至为零，因此内聚刚度在理论上是无穷大的．内聚刚度反映了内聚界面的强弱，足够大的内聚刚度能够保证结构在开裂之前是一个整体，但是内聚刚度取值过大往往会使得界面发生能量的突然耗散，从而导致有限元解产生数值振荡出现收敛问题，为此ABAQUS中引入了黏结系数来调整材料的刚度矩阵，通过修改损伤因子来调整牵引分离定律的软化曲线从而克服收敛困难问题[27]．修改后的损伤因子

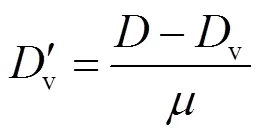
式中：为材料的损伤因子；v为黏性刚度退化变量；为黏结系数，通常取值为10-5～10-2．

2 三峡钢衬钢筋混凝土管道开裂分析

2.1 计算模型

三峡水电站压力管道内径为12.4m，最大内水压力为1.21MPa，引水钢管布置在坝下游面，采用钢衬钢筋混凝土结构形式．本文基于三峡水电站钢衬钢筋混凝土压力管道1∶2大比尺模型试验数据[3]建立三维有限元模型如图6所示，顺水流向管段长度为0.6m，钢衬厚度为16mm，材料和配筋率均与原型一致，内层布置28@200钢筋，中层布置32@200钢筋，外层布置36@200钢筋，具体材料参数见表1．钢筋采用埋入式模型，并假定钢筋与混凝土之间不发生滑移，钢衬与外包混凝土之间采用面面接触，摩擦系数取为0.5．采用共节点连接方式在管道混凝土中全局插入内聚单元进而模拟管道混凝土的随机开裂，内聚参数取值由混凝土直拉试验确定，内聚刚度根据Zou等[28]的建议取为最大内聚力的106倍，具体参数取值见表1．模型底部施加全约束，不考虑水重和结构自重的影响．

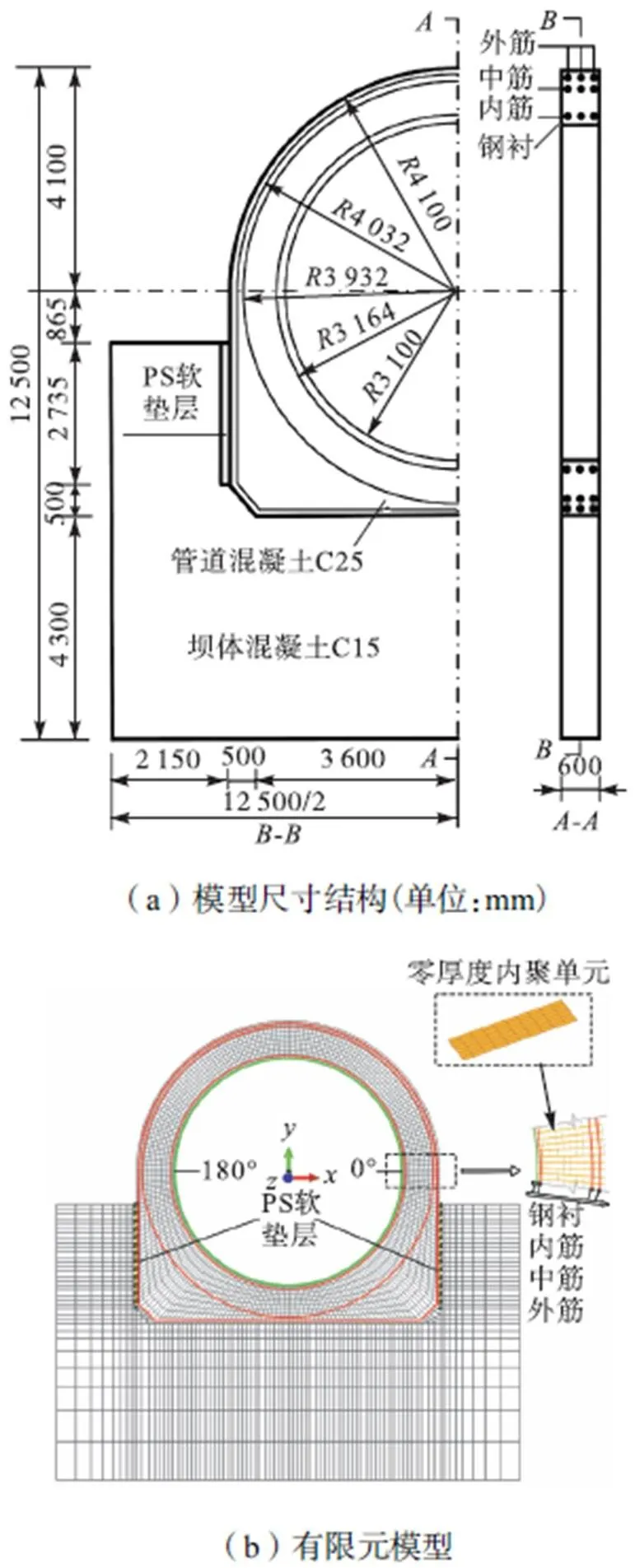
图6 三峡水电站模型试验尺寸及其有限元模型

表1 三峡水电站模型试验材料参数与内聚区域计算参数

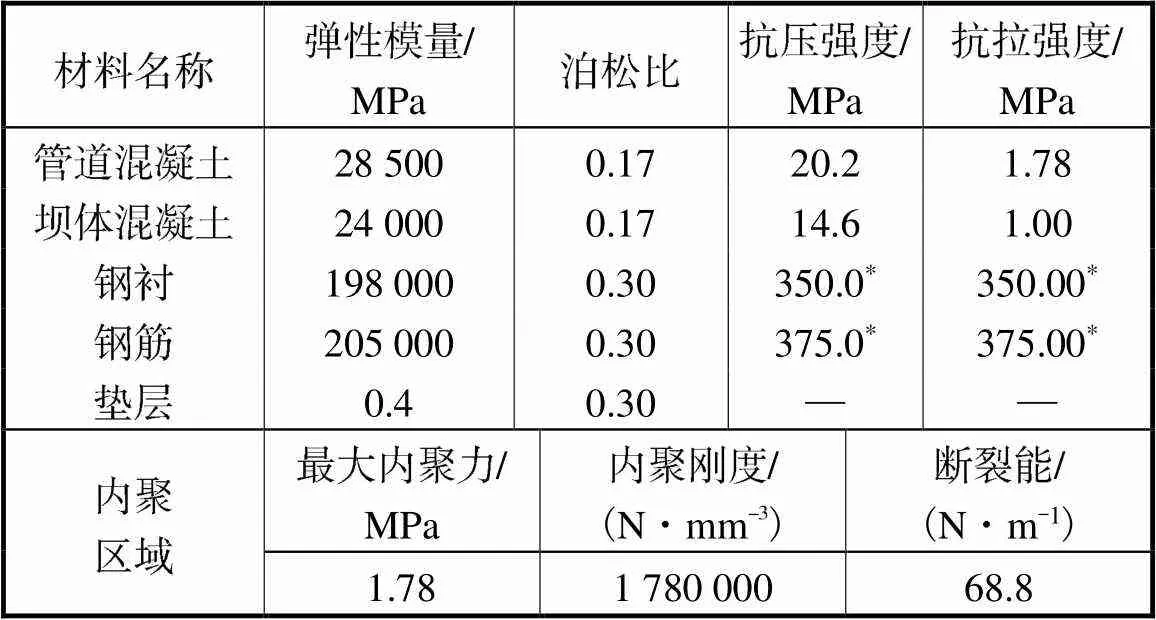
Tab.1 Model test material parameters and cohesive process zone parameters of the Three Gorges Hy-dropower Station

注：“*”代表钢材的屈服强度.

2.2 混凝土裂缝扩展规律及裂缝形态

在内水压力作用下，管道混凝土主要承受环向拉应力，产生径向裂缝，其开裂过程如图7所示，下角标为裂缝出现的顺序．

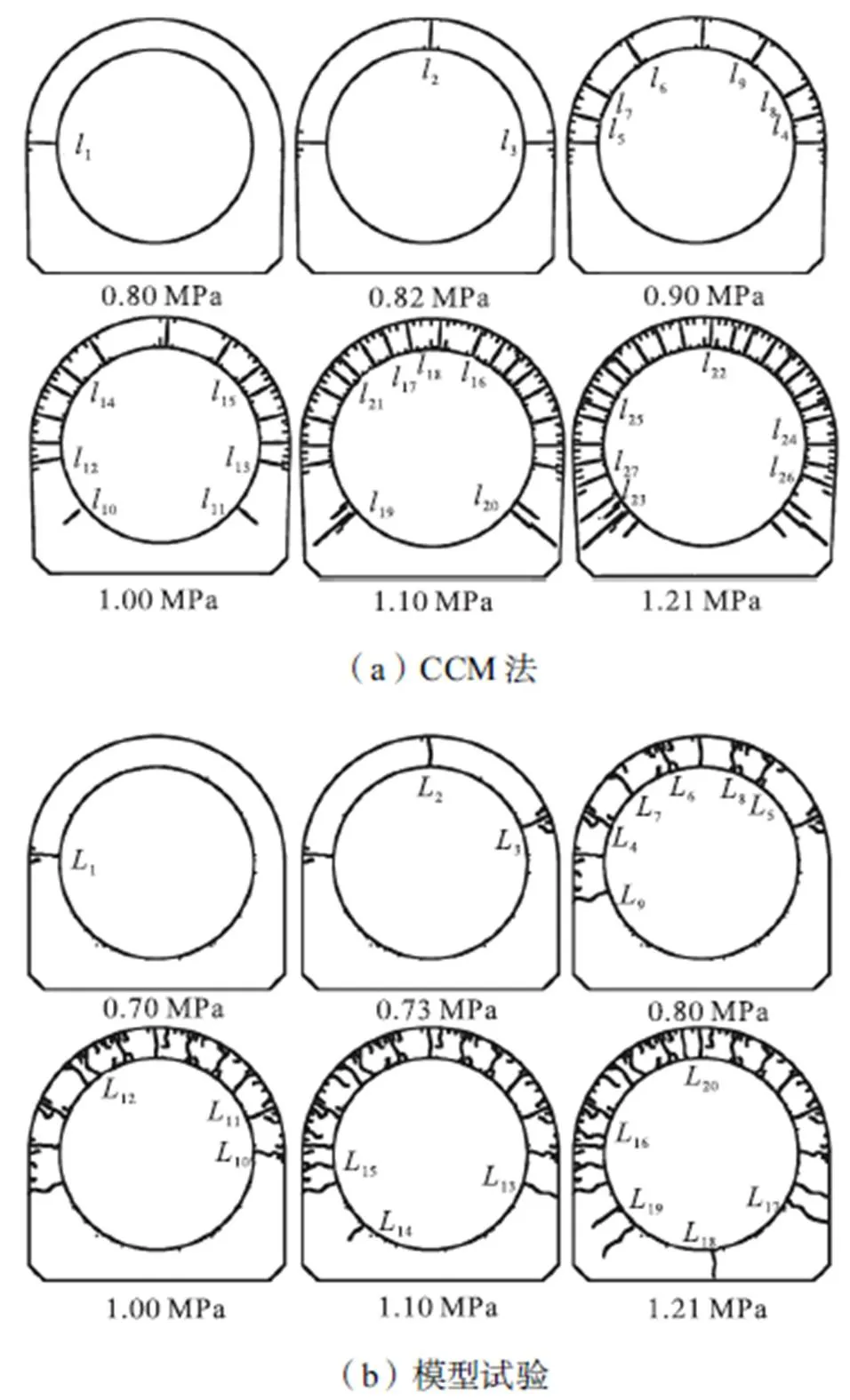
图7 管道混凝土损伤开裂过程

用CCM法模拟混凝土开裂时，在设计荷载下，管道一共出现26条贯穿性裂缝：上半部管道裂缝条数多而密，分布均匀；下半部裂缝少而稀，裂缝分布基本左右对称．第1条裂缝发生在180°断面附近，初裂荷载为0.80MPa．第2条和第3条裂缝分别发生在90°、0°断面附近．随着内压增大，管道混凝土持续损伤开裂，管道下半部也逐渐产生裂缝，最终沿管周形成径向分布的裂缝．对比模型试验管道混凝土开裂过程图发现，在设计荷载下模型试验共出现20条径向贯穿裂缝，第1条裂缝发生在管腰截面175°位置，初裂荷载为0.70MPa，与CCM法起裂荷载和起裂位置基本一致，由此可见CCM法得到的裂缝分布情况和裂缝开展规律与模型试验吻合良好．

分析裂缝的开裂形态(如图8所示)可知，对于任意开裂截面而言，由于钢筋的作用，管壁内侧和外壁的裂缝宽度均小于中部，呈“眼睛”形状，与模型试验裂缝宽度管壁中间宽、两侧较小的结果一致．

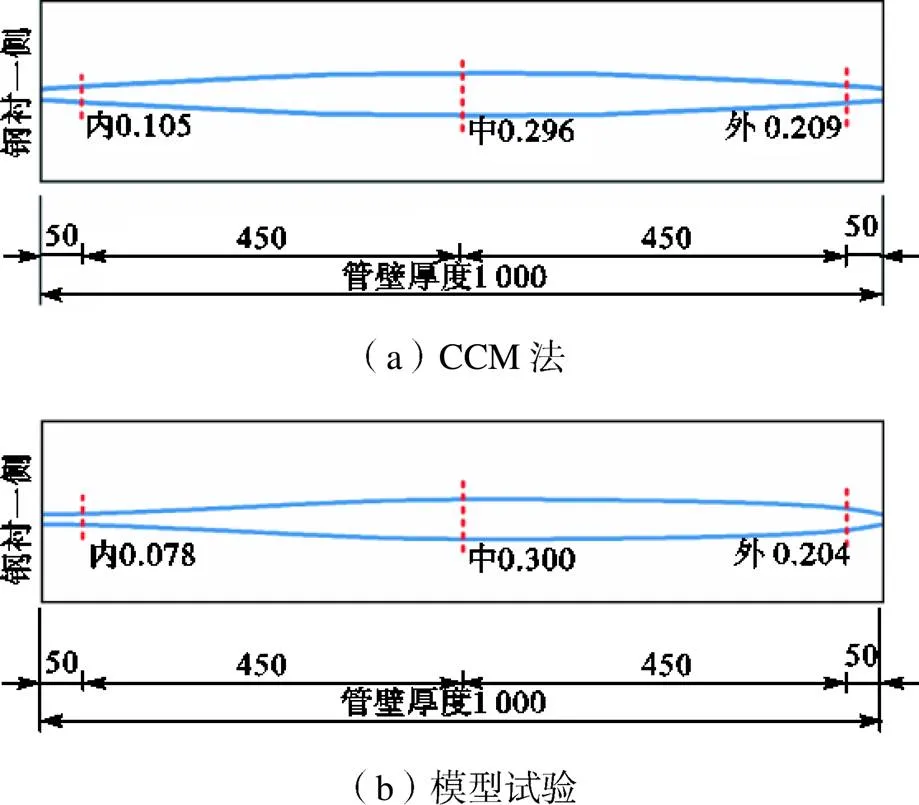
图8 管道腰部裂缝L1的形态(1.21MPa，单位：mm)

2.3 混凝土裂缝宽度分析

内聚单元无法输出裂缝宽度，可通过获得内聚单元体积的改变量除以内聚单元的面积获得模型的平均缝宽[29]．本文采用零厚度的内聚单元模拟混凝土的开裂，由于预先定义了内聚单元的开裂方向，即沿着管道的径向开裂，此时管道的开裂宽度等于内聚单元上下表面在环向上的相对位移．

提取管腰左侧(180°)裂缝1、顶部(90°)裂缝2和管腰右侧(0°)裂缝3的裂缝宽度结果如图9所示，从图中可以看出，当内水压力达到起裂荷载时，混凝土拉应力迅速减小，裂缝宽度突然增加，能量瞬间释放，形成初始裂缝．随着内水压力的持续增加，裂纹持续扩展缝宽增加，在内水压力达到1.10MPa时裂纹扩展趋于稳定，在最大内水压力作用下达到最大值．裂缝宽度中部最宽，外侧次之，内侧最小，因此中层钢筋靠外层布置可以提高外侧含筋量，从而有效减小裂缝宽度．在设计内水压力下，裂缝宽度最大值大于规范中混凝土最大裂缝宽度0.3mm的限值，因此可结合CCM法进一步讨论最大裂缝宽度的规定．

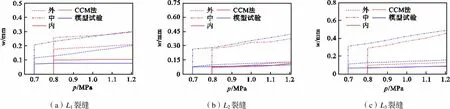
（a）L1裂缝（b）L2裂缝（c）L3裂缝

为了验证有限元解的准确性，将本文的计算结果三峡大比尺模型试验的结果进行对比，结果表明，数值法与模型试验的结果吻合良好．两种方法3条裂缝的最大误差均在混凝土起裂初期最大，这是因为有限元模拟时未考虑混凝土的初始裂缝的影响，而管道混凝土在受拉开裂前就已经存在局部微裂缝，随着混凝土损伤开裂的发展，CCM法得到的裂缝宽度越来越接近实际情况．

3 钢材应力分布规律及承载特性

在内水压力作用下，管道外包混凝土开裂产生裂缝，混凝土应力释放引起管道应力重分布，从而影响管道的联合承载特性．分析管顶、管底和左右两腰典型部位的钢材应力值(图10)可知，混凝土在开裂之前钢衬和钢筋的应力均较小，混凝土承担大部分内水压力，混凝土在达到起裂荷载以后，钢材应力迅速增大，且随内水压力增加呈线性增加．钢筋应力整体上中筋最大，外筋次之，内筋最小．钢材应力整体上在60～180MPa范围内，未达到钢材应力屈服极限. CCM法模拟时在弹性阶段与模型试验的误差大于塑性阶段，分析原因可能是管道混凝土初始微观裂缝的存在，部分混凝土应力释放由钢材承担，而有限元模拟时假定混凝土初始裂缝之前为线弹性材料，使得模型试验钢材应力值略大于CCM法．

为进一步分析混凝土开裂后钢材应力的变化和承载特性，从管底开始对钢材定义顺时针单位化的环向路径NDP(0～1表示从管底沿顺时针一圈0°～360°的值，管底为0，管顶为0.5)，钢材应力环向分布情况如图11～图14所示．分析可知，钢材应力分布不仅与结构的部位有关，同时与结构裂缝密切相关．整体上管道上半部钢材应力大于下半部，裂缝处钢筋应力较大，非裂缝处钢筋应力较小．钢衬应力在开裂前环向分布均匀，开裂使得钢衬应力不均匀性显著增加，管道底部与坝体大体积混凝土相连，损伤较小，钢衬底部应力仍较为均匀．钢筋应力起伏较大，CCM法可以很好地模拟裂缝处钢材应力突变的现象．此外钢材应力大小与钢筋位置也有关，管道上半周内筋应力较小，中筋和外筋应力较大，因此可以将内层钢筋靠外层布置以充分发挥钢衬的抗拉作用，以达到节约钢材降低工程造价的作用．

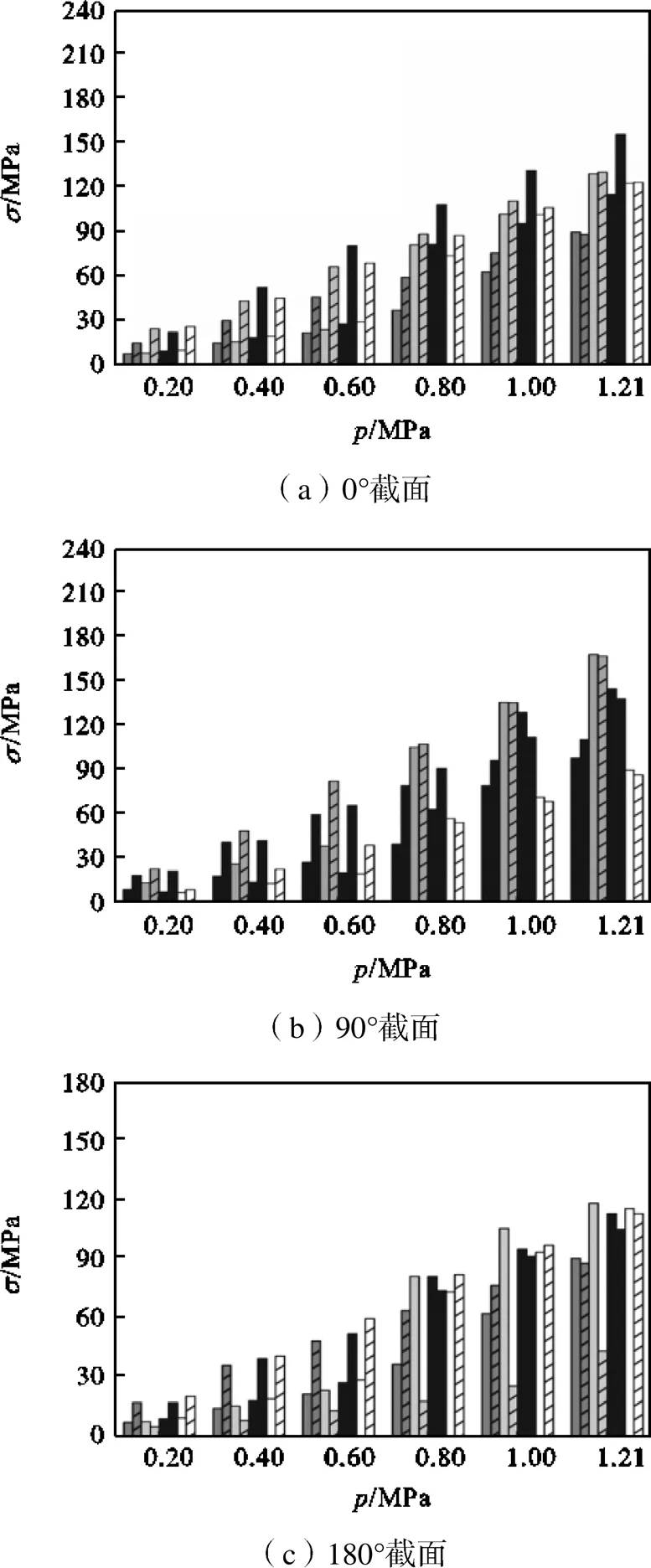
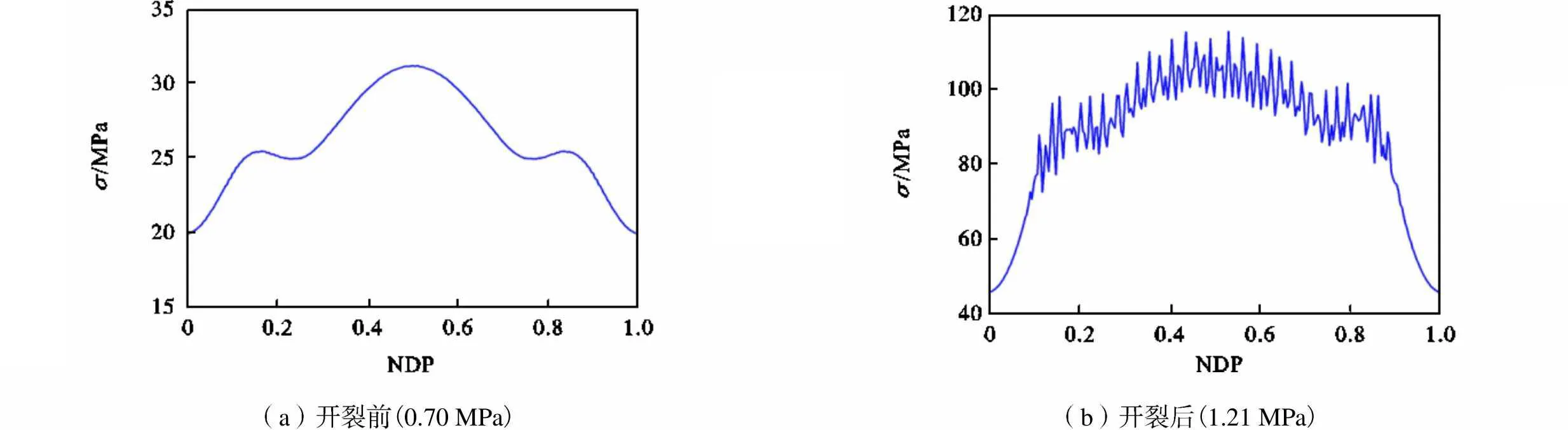
（a）开裂前(0.70MPa)（b）开裂后(1.21MPa)

（a）开裂前(0.70MPa)（b）开裂后(1.21MPa)

（a）开裂前(0.70MPa)（b）开裂后(1.21MPa)

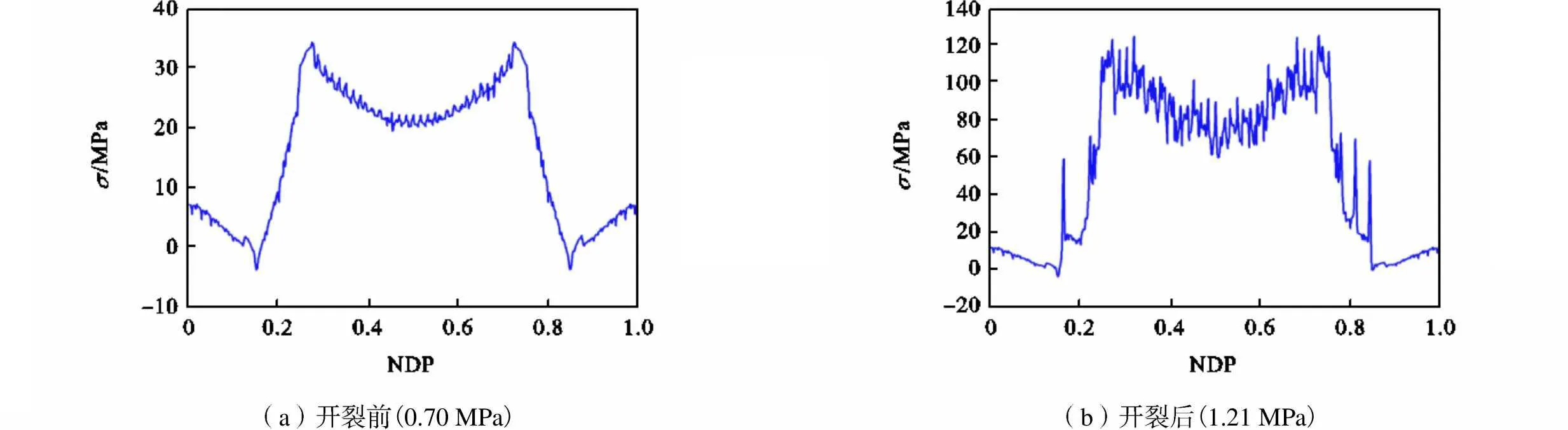
（a）开裂前(0.70MPa)（b）开裂后(1.21MPa)

4 内聚参数和网格尺寸敏感性分析

在材料中插入内聚界面，会引起整体刚度的下降，内聚刚度的取值是内聚单元能否很好地模拟混凝土开裂的关键，因此有必要探究内聚刚度的取值问题，以减弱甚至消除内聚单元的影响[30]．本文根据Zou等[28]的建议将内聚单元的刚度取值为混凝土抗拉强度105、106、107倍3种情况，其计算结果如图15所示．分析发现，内聚刚度取值越小，内聚区域在荷载作用下表现越软弱，混凝土开裂时间越早．这是由于内聚刚度控制内聚单元的弹性行为的同时也影响了内聚区域的非弹性行为，如图16所示，内聚单元的未损伤应力u等于内聚刚度与单元位移的乘积，因此内聚刚度的取值直接影响内聚表面进入非线性阶段产生裂缝的时机．同时分析裂缝宽度随内水压力变化曲线发现，随着内水压力的增加，裂缝宽度计算结果越来越接近，说明混凝土裂缝的长期发展受内聚刚度影响较小．其原因可能是裂缝宽度的长期发展主要受应力-位移曲线尾部的影响，而尾部受内聚刚度的影响可以忽略不计．钢材应力在开裂前不同刚度取值结果差异较大，开裂后随着内水压力增加结果亦越来越接近，因此内聚刚度的取值主要影响混凝土的开裂时机，对最终裂缝宽度和钢材应力的计算结果影响较小，为较为准确地模拟混凝土开裂的时机同时保证计算的收敛性和高效性，本文内聚刚度取值建议取为1780000N/mm3．

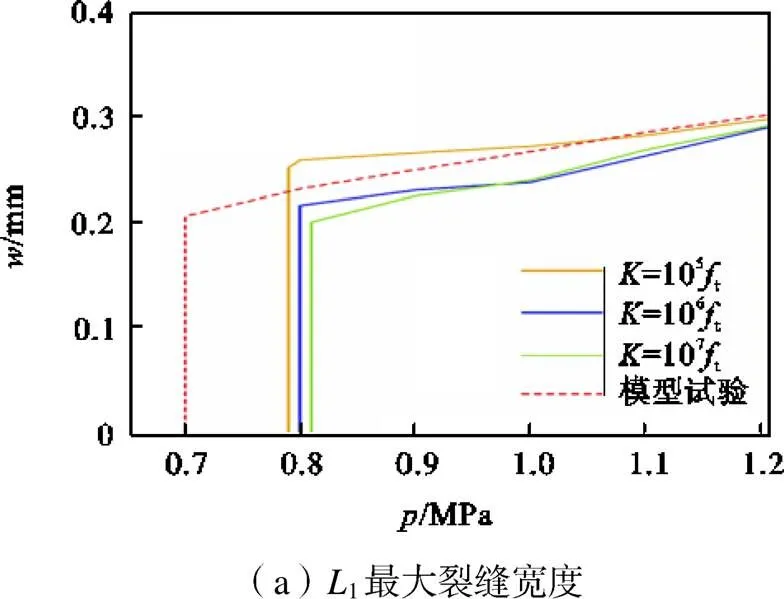
图16 由损伤参数确定残余应力

前文提到材料在软化过程中刚度下降将造成数值解的收敛性问题，引入黏结系数可以调整软化过程的损伤因子，从而促进解的收敛．本文分别取黏结系数为1×10-3、1×10-4、1×10-5和1×10-64种情况探究黏结系数取值不同对管道开裂过程中钢材应力和裂缝宽度的影响，如图17所示．分析可知，当采用1×10-6时解不能收敛，黏结系数取值为1×10-5时与模型试验结果吻合最好．黏结系数取值越大越容易收敛，计算效率越高，但是结果精确性也在下降，因此在保证收敛的情况下应尽可能取较小的黏结系数，本文中的黏结系数建议取为1×10-5．同时考虑到计算的效率，当对解的精度要求不高时，可适当提高黏结系数取值．

图17 黏结系数对管道开裂的影响

网格划分的精密性直接影响内聚单元模拟混凝土开裂的非线性过程，网格尺寸对管道混凝土开裂的影响分析如图18所示．分析可知，当网格比较稀疏的时候黏聚裂缝模型的结果与模型试验误差较大，网格越精密误差越小．综合考虑计算效率和计算精度，当单元网格尺寸取为0.032(管道内径)时已经可以很好地模拟管道混凝土的开裂过程．

图18 网格尺寸对管道开裂的影响

5 结 论

本文结合三峡水电站大比尺钢衬钢筋混凝土管道模型试验，基于断裂力学和损伤力学理论，用内聚区域的牵引分离定律来描述混凝土材料开裂的损伤和断裂特性，采用内聚裂缝的有限元模型研究了管道混凝土裂缝扩展规律、裂缝宽度、钢材应力分布规律与承载特性，并与其模型试验结果进行了对比，结论如下．

(1) CCM法模拟的裂缝发展规律、裂缝宽度结果与模型试验吻合良好，且二者的结果都超过了规范中混凝土最大裂缝宽度0.3mm的限值，因此可结合CCM法进一步探讨钢衬钢筋混凝土管道最大裂缝宽度限值的规定．

(2) CCM法模拟的裂缝形态呈“眼睛”形状，中间最宽两侧较小，钢筋应力与裂缝形态相对应也呈现同样的规律．CCM真实地模拟了混凝土受拉张开的过程，反映了裂缝处钢材应力急剧增加的过程，得到的钢材应力结果与模型试验基本一致，可为管道配筋和钢筋的布置提供参考．

(3) 更改内聚参数，即内聚刚度、黏结系数以及单元网格密度发现，在合理的取值范围内，CCM法可以很好地模拟管道的开裂非线性过程，得到的裂缝宽度和钢材应力精度较高．

因此，综合考虑混凝土断裂和损伤的黏聚裂缝模型可以避开传统有限元分析网格重剖或者无法直接计算得到裂缝宽度的难题，合理地模拟管道混凝土的开裂非线性过程，为管道的安全和耐久性评估提供依据．

［1］ 伍鹤皋，马 铢，石长征. 坝下游面钢衬钢筋混凝土管道结构研究综述[J]. 水力发电学报，2020，39(11)：1-12.

Wu Hegao，Ma Zhu，Shi Changzheng. Overview of research and engineering application of steel-lined reinforced concrete penstocks laid on downstream dam surfaces[J]. Journal of Hydroelectric Engineering，2020，39(11)：1-12(in Chinese).

［2］ 杨和风，刘 诚. 依萨河二级水电站压力管道现场水压试验[J]. 云南水力发电，1995(1)：26-30.

Yang Hefeng，Liu Cheng. On site hydraulic test of penstock of Yisa River cascade Ⅱ hydropower station[J]. Yunnan Water Power，1995(1)：26-30(in Chinese).

［3］ Wu Hegao，Gosling P D. Structural research on the penstocks for Three Gorges[J]. Hydropower & Dams，2000(1)：64-68.

［4］ 宋常春，赵贵发，张自敬，等. 东江双曲拱坝坝后式引水管道的设计与施工[J]. 水力发电，1987(11)：38-43.

Song Changchun，Zhao Guifa，Zhang Zijing，et al. Design and construction of diversion pipeline of Dong-jiang double curvature arch dam[J]. Water Power，1987(11)：38-43(in Chinese).

［5］ 蒋锁红. 坝后背管结构力学弹性中心法的应用[J]. 水力发电，2003(9)：31-34.

Jiang Suohong. Application of the elasticity center method of structure mechanics for penstock laid on the downstream face of dam[J]. Water Power，2003(9)：31-34(in Chinese).

［6］ 董哲仁，董福品，鲁一晖. 钢衬钢筋混凝土压力管道混凝土裂缝宽度数学模型[J]. 水力发电，1996(5)：39-42.

Dong Zheren，Dong Fupin，Lu Yihui. Mathematics model of concrete crack width on the steel-lined reinforcement concrete penstock[J]. Water Power，1996 (5)：39-42(in Chinese).

［7］ 董哲仁. 下游坝面压力管道混凝土正交异性状态应力计算[J]. 水利学报，1986(1)：31-37.

Dong Zheren. The stress calculation of penstocks placed on downstream dam faces and surrounded by reinforced concrete in orthotropic condition[J]. Journal of Hydraulic Engineering，1986(1)：31-37(in Chinese).

［8］ 王康平，伏义淑，邱卫民. 钢衬钢筋混凝土压力管道裂缝计算公式研究[J]. 武汉水利电力大学(宜昌)学报，2000，22(4)：278-282.

Wang Kangping，Fu Yishu，Qiu Weimin. Research on formulas for calculating crack width of penstocks with inner steel liner and outer reinforced concrete[J]. Journal of Wuhan University of Hydraulic and Electric Engineering(Yichang)，2000，22(4)：278-282(in Chinese).

［9］ 王康平，伏义淑，田 斌. 大坝背管裂缝宽度计算公式的改进[J]. 三峡大学学报(自然科学版)，2001，23(5)：396-401.

Wang Kangping，Fu Yishu，Tian Bin. Improvement in formula for calculating cracking width of back-pipeline of dam[J]. Journal of China Three Gorges University(Natural Sciences)，2001，23(5)：396-401(in Chinese).

［10］ 伍鹤皋，马善定. 三峡水电站压力管道非线性有限元分析[J]. 武汉水利电力大学学报，1994，27(6)：643-648.

Wu Hegao，Ma Shanding. Nonlinear finite element ana-lysis of penstocks of the Three Gorges Hydropower Station[J]. Journal of Wuhan University of Hydraulic and Electric Engineering，1994，27(6)：643-648(in Chinese).

［11］ 石长征，伍鹤皋，苏 凯. 有限单元法和弹性中心法在坝后背管结构设计中的应用比较[J]. 水利学报，2010，41(7)：856-861.

Shi Changzheng，Wu Hegao，Su Kai. Applications of FEM and elasticity centre method of structure mechanics in designing penstock laid on downstream surface of dam[J]. Journal of Hydraulic Engineering，2010，41(7)：856-861(in Chinese).

［12］ 苏 凯，杨子娟，伍鹤皋，等. 缝隙对钢衬钢筋混凝土管道结构承载特性的影响研究[J]. 天津大学学报(自然科学与工程技术版)，2018，51(9)：967-976.

Su Kai，Yang Zijuan，Wu Hegao，et al. Influence of gap on bearing mechanism of steel-lined reinforced concrete penstock[J]. Journal of Tianjin University(Science and Technology)，2018，51(9)：967-976(in Chinese).

［13］ 石长征，伍鹤皋. 水电站坝下游面钢衬钢筋混凝土管道损伤和承载特性[J]. 天津大学学报(自然科学与工程技术版)，2014，47(12)：1081-1087.

Shi Changzheng，Wu Hegao. Damage and bearing characteristics of steel lined reinforced concrete penstock on downstream face of dam in hydropower station[J]. Journal of Tianjin University(Science and Technol-ogy)，2014，47(12)：1081-1087(in Chinese).

［14］ Dong W，Wu Z，Zhou X，et al. FPZ evolution of mixed mode fracture in concrete：Experimental and numerical[J]. Engineering Failure Analysis，2017，75：54-70.

［15］ Chao X，Qi L，Tian W，et al. Evaluation for interfacial fracture of fiber-reinforced pyrocarbon matrix composites by using a zero-thickness cohesive approach[J]. Journal of Alloys and Compounds，2020，820：153378.

［16］ 计宏伟，陈金龙，秦玉文. 复合材料黏接界面缺陷的热象无损检测和定量评价[J]. 天津大学学报，2001，34(2)：221-224.

Ji Hongwei，Chen Jinlong，Qin Yuwen. Nondestruc-tive evaluation of quality of adhesive in terface of composite structures by using thermal imaging technique[J] Journal of Tianjin University，2001，34 (2)：221-224(in Chinese).

［17］ Dugdale D S. Yielding of steel sheets containing slits[J]. Journal of the Mechanics and Physics of Solids，1960，8(2)：100-104.

［18］ Hillerborg A，Modéer M，Petersson P-E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements[J]. Cement & Concrete Research，1976，6(6)：773-781.

［19］ 薛 亮，孙千伟，任晓丹. 基于内聚单元模型的装配式剪力墙数值模拟研究[J]. 地震工程与工程振动，2020，40(4)：174-182.

Xue Liang，Sun Qianwei，Ren Xiaodan. Numerical investigation of hysterical behaviors of assembled shear wall based on cohesive element model[J]. Earthquake Engineering and Engineering Vibration，2020，40(4)：174-182(in Chinese).

［20］ Alfano G. On the influence of the shape of the interface law on the application of cohesive-zone models[J]. Composites Science and Technology，2006，66(6)：723-730.

［21］ 蔡改贫，宣律伟，张雪涛，等. 多尺度内聚颗粒模型破碎过程研究[J]. 岩土力学，2020，41(6)：1809-1817.

Cai Gaipin，Xuan Lüwei，Zhang Xuetao，et al. Investigation into the crushing process in multi-scale cohesive particle model[J]. Rock and Soil Mechanics，2020，41(6)：1809-1817(in Chinese).

［22］ Yang Q，Cox B. Cohesive models for damage evolution in laminated composites[J]. International Journal of Fracture，2005，133(2)：107-137.

［23］ 曹祖同，陈云霞，秦怀泉. 断裂力学方法分析钢筋混凝土的抗裂度[J]. 天津大学学报，1992，25(4)：91-99.

Cao Zutong，Chen Yunxia，Qin Huaiquan. Analysis of cracking resistance strength of reinforced concrete by fracture mechanics[J]. Journal of Tianjin University，1992，25(4)：91-99(in Chinese).

［24］ Su R K L，Chen H H，Fok S L，et al. Determination of the tension softening curve of nuclear graphites using the incremental displacement collocation method[J]. Carbon，2013，57：65-78.

［25］ Yang S T，Li K F，Li C Q. Numerical determination of concrete crack width for corrosion-affected concrete structures[J]. Computers & Structures，2018，207：75-82.

［26］ Turon A，Dávila C G，Camanho P P，et al. An engineering solution for mesh size effects in the simulation of delamination using cohesive zone models[J]. Engineering Fracture Mechanics，2007，74(10)：1665-1682.

［27］ Yang S，Li C. Numerical prediction for corrosion-induced concrete crack width[J]. Proceedings of the Institution of Civil Engineers Construction Materials，2011，164(6)：293-303.

［28］ Zou Z，Reid S R，Li S，et al. Modelling interlaminar and intralaminar damage in filament-wound pipes under quasi-static indentation[J]. Journal of Composite Materials，2002，36(4)：477-499.

［29］ 沈子豪. 开裂混凝土细观模拟及力学性能研究[D]. 武汉：湖北工业大学，2020.

Shen Zihao. Mesoscopic Simulation and Mechanical Properties of Cracked Concrete[D]. Wuhan：Hubei University of Technology，2020(in Chinese).

［30］ Sedlacek F，Kalina T，Raz K. Determination of interlaminar fracture toughness of CFRP composite in mode I using numerical simulation with cohesive elements[J]. Key Engineering Materials，2020，847：15-21.

Research on the Cracking Mechanism and Simulation Technology of Steel-Lined Reinforced Concrete Penstock

Ma Zhu，Wu Hegao，Shi Changzheng

(State Key Laboratory of Water Resources and Hydropower Engineering Science，Wuhan University，Wuhan 430072，China)

Steel-lined reinforced concrete penstock is designed to allow concrete cracks. The crack propagation and bearing characteristics of the penstock after having cracks is a prerequisite for assessing whether the pipe can operate safely and stably for a long time. However，the existing formulas of steel stress and crack width are mostly semi-empirical that do not agree with each other. As a result，the finite element model gradually became the most popular analysis method instead of an analytical approach. Existing finite element methods are primarily based on damage or fracture theory and are rarely considered to have a coupling effect. In this study，a finite element model based on a cohesive crack model is developed using a large-scale test model of the Three Gorges Hydropower Station. Cohesive elements are inserted into the concrete pipe to simulate damage and fracture characteristics in concrete cracking and obtain the structure bearing characteristics，crack propagation，and crack width. Furthermore，cohesive parameters and element size are discussed systematically and show that the finite element simulation and model test are in good agreement. The cracks are in the shape of‘eyes’，consistent with the width of the model test that is wide in the middle and small on both sides. The results show that the error of the crack width between the cohesive crack model and model test is less than 10%，and the stress fluctuation of steel corresponds to the crack. Finite element simulation can get accurate results within a reasonable range by changing the cohesive parameters and element size. However，too small penalty stiffness will lead to the early cracking of concrete，and too large viscous regularization or element size will reduce the accuracy of calculation results. Hence，a smaller viscous regularization coefficient and a larger penalty stiffness are necessary as much as possible on the premise of ensuring the convergence of calculation when the cohesive model is used to simulate the cracking of concrete.

steel-lined reinforced concrete penstock；numerical simulation；cohesive crack model；crack propagation；crack width；bearing characteristics

TV732.4

A

0493-2137(2022)01-0046-11

10.11784/tdxbz202102023

2021-02-20；

2021-03-15.

马 铢（1996—  ），女，博士研究生，mazhu0518@whu.edu.cn．

伍鹤皋，wbf1988@vip.sina.com.

国家重点研发计划资助项目(2016YFC0401803).

Supported by the National Key Research and Development Program of China (No. 2016YFC0401803).

(责任编辑：金顺爱)