勇闯中考的“三数”关

文／胡焕过

数据的集中趋势和离散程度是中考数学考查的热点内容。随着考查的不断深入，此类问题的创新性、综合性也更强，出现了一批背景丰富、考点全面、题型新颖、贴近生活的题型。下面，我们就一起走入2022年中考现场。

“三数”，即平均数、中位数、众数，从不同的角度给我们提供了一组数据的面貌特征。正因为如此，我们把这三个数作为一组数据集中趋势的代表。

考点1 平均数的应用

例1（2022·浙江杭州）某校学生会要在甲、乙两位候选人中选择一人担任文艺部干事，对他们进行了文化水平、艺术水平、组织能力的测试，根据综合成绩择优录取。他们的各项成绩（单项满分100分）如表所示：

候选人甲 乙文化水平80分80分艺术水平87分96分组织能力82分76分

（1）如果把各项成绩的平均数作为综合成绩，应该录取谁？

（2）如果想录取一名组织能力较强的候选人，把文化水平、艺术水平、组织能力三项成绩分别按照20%、20%、60%的比例计入综合成绩，应该录取谁？

【分析】（1）根据题意，求这组数据的算术平均数，再通过比较大小作出决策；（2）与（1）有区别，文化水平、艺术水平、组织能力三项成绩的重要程度不相同，分别占20%、20%、60%。我们把衡量各个数据“重要程度”的数值称为“权”。根据题意，这一问求的是这组数据的加权平均数，再通过比较大小作出决策。

解：（1）甲的综合成绩为=83（分），乙的综合成绩为84（分）。因为乙的综合成绩比甲的高，所以应该录取乙。

（2）甲 的 综 合 成 绩 为80×20%+87×20%+82×60%=82.6（分），乙的综合成绩为80×20%+96×20%+76×60%=80.8（分）。因为甲的综合成绩比乙的高，所以应该录取甲。

【点评】本题主要考查平均数的运用，解题的关键是区分算术平均数与加权平均数的概念和熟练掌握两者的计算公式。

考点2 中位数和众数的应用

例2（2022·河北）五名同学捐款数分别是5，3，6，5，10（单位：元），捐10元的同学后来又追加了10元。追加后的5个数据与之前的5个数据相比，集中趋势相同的是（ ）。

A.只有平均数

B.只有中位数

C.只有众数

D.中位数和众数

【分析】分别计算前后数据的平均数、中位数、众数，比较即可得出答案。

解：追加前，平均数为

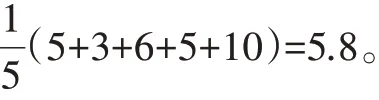
从小到大排列为3，5，5，6，10，则中位数为5。5出现次数最多，众数为5。

追加后，平均数为

从小到大排列为3，5，5，6，20，则中位数为5。5出现次数最多，众数为5。

综上，中位数和众数都没有改变。

故选D。

【点评】本题综合考查了平均数、中位数与众数的运用。我们要注意以下几点：（1）求平均数需要全组所有数据，其中任何数据的变动都会引起平均数变动。平均数反映了一组数据的总体水平，易受极端值的影响。（2）求中位数需要把数据先按大小顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数；如果数据的个数是偶数，则处于中间位置的两个数的平均数就是这组数据的中位数。某些数据的变动对中位数没有影响，中位数反映了一组数据的中等水平，不易受极端值的影响。（3）众数与数据出现的次数有关，结果可以不唯一。众数反映了一组数据的多数水平，不易受极端值的影响。