增减统计信息 提升分析能力

文／蒋志恒

同学们，我们正快速行进于信息时代，面对一些具体问题，从数据中获取信息、通过信息的分析进行判断和决策是我们必备的能力之一。本篇我们尝试对一些统计问题进行变化——在问题中增加或减少信息，以培养同学们相应的变式能力。

一、增加信息量，提升整体感知的能力

例1下图是某市连续5天的气温情况。

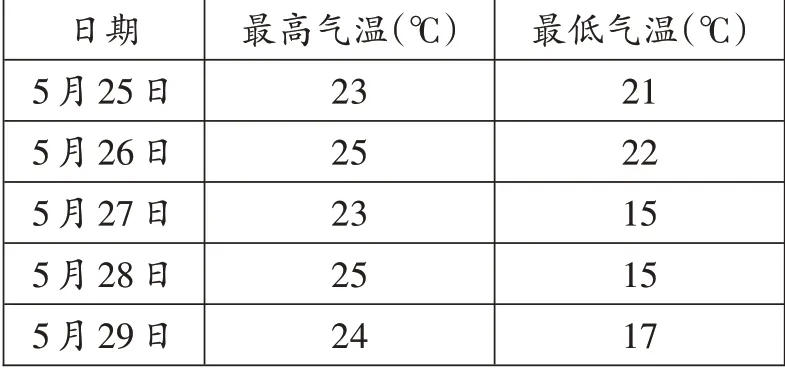
日期5月25日5月26日5月27日5月28日5月29日最高气温（℃）23 25 23 25 24最低气温（℃）21 22 15 15 17

利用方差判断该市这5天的日最高气温波动大还是日最低气温波动大。

【解析】此题考查平均数、方差的计算，还需要理解方差是判断数据波动程度最常用的统计量之一。这5天的日最高气温和日最低气温的平均数分别是

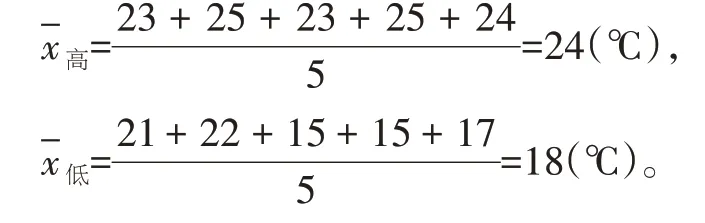
由s高2＜s低2可知，这5天的日最低气温的波动较大。

【变式】下图是某市连续5天的天气情况。

（1）利用方差判断该市这5天的日最高气温波动大还是日最低气温波动大；

（2）根据上图提供的信息，请再写出两个不同类型的结论。

【解析】第（1）问与原题一样，对于变式题的第（2）问，很多同学会就单一的方面写出结论。例如：5月26日的最低气温比5月27日的最低气温高，5月26日和5月28日的最高气温一样等。这样的结论当然没错，但缺乏对天气情况的整体认识。仔细观察该天气情况中的信息，共有“天气现象”“最高气温”“最低气温”“空气质量”这4个方面的数据和情况，要想整体认识，就要联系其中至少两个方面得出结论。25日、26日、27日、28日、29日的天气现象依次是大雨、中雨、晴、晴、多云，日温差依次是2℃、3℃、8℃、10℃、7℃，可以看出雨天的日温差较小；25日、26日、27日的天气现象依次是大雨、中雨、晴，空气质量依次是良、优、优，说明下雨后空气质量改善了；等等。

二、减少信息量，提升深入挖掘的能力

例2图1为某班35名学生投篮成绩的条形图，则此班学生投篮成绩的中位数是___。

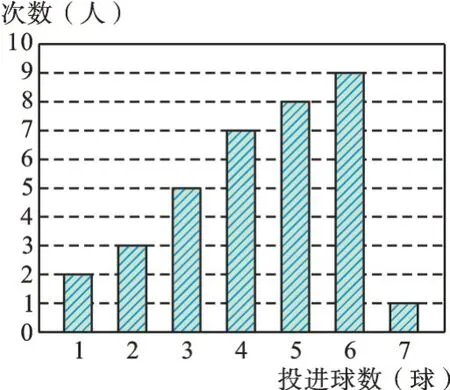
图1

【解析】此题考查对条形统计图的理解和中位数的计算。将35人投篮成绩按大小顺序排列后，应取第18个人的成绩作为此班学生投篮成绩的中位数。故填5球。

【变式】图2为某班35名学生投篮成绩的条形图，但部分数据破损导致数据不完全。已知此班学生投篮成绩的中位数是5球，则根据图2，下列数值无法确定的是（ ）。

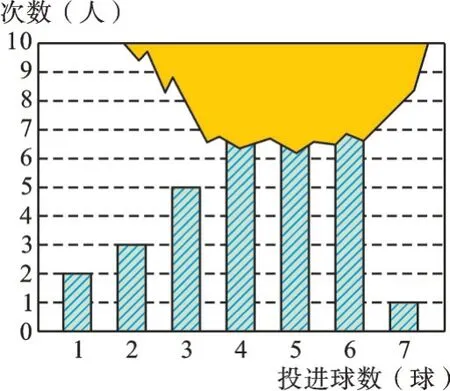
图2

A.3球以下（含3球）的人数

B.4球以下（含4球）的人数

C.5球以下（含5球）的人数

D.6球以下（含6球）的人数

【解析】本题与例2不同的是，已经知道该班学生投篮成绩的中位数是5球，但不知道投进4球、5球和6球的学生人数。我们利用总人数可知，第18个人的成绩是5球。根据条形统计图可知，3球以下（含3球）的人数是10人；4球的人数超过6人，即至少为7人，所以4球以下（含4球）的人数至少为17人，再根据第18个人的成绩是5球可知，4球以下（含4球）的人数至多为17人，所以4球以下（含4球）的人数就是17人；5球以下（含5球）的人数无法确定；6球以下（含6球）的人数是35-1=34（人）。故选C。同学们发现了吗，解决本题的关键是需要知道投进4球、5球和6球的学生人数都大于6人，这需要仔细观察这张残缺的统计图才行，它是我们深入挖掘信息的基础。