关注数据分布，把握统计量本质

文／曹 阳

大数据时代，数据无处不在，无处不用。我们要通过数据认识世界，感受统计知识在实际问题中的应用。但有时，我们并不需要精确的个体数据和统计量的值，只要关注数据的分布情况就能解决问题。这就更需要我们把握统计量的本质，提升解决统计问题的能力。

一、通过数据分布获得中位数与众数

例1某校根据九年级学生期末考试成绩在年级中的位次，从高到低把学生成绩评定为5个等第：A+、A、B、C、D，各等第人数分布的扇形统计图如下。

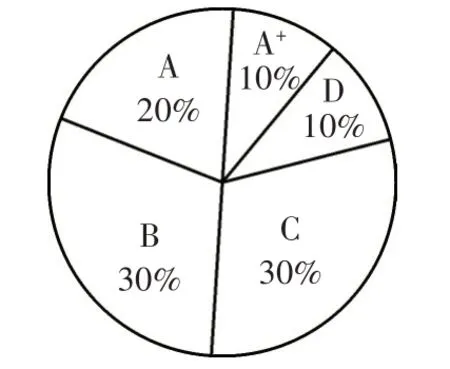
某校九年级期末考试各等第人数分布扇形统计图

（1）由图可知，这次考试成绩的中位数应被评定为______等第；

（2）这次考试成绩的众数一定被评定为B或C等第吗？说明理由。

【分析】本题结合扇形统计图考查中位数和众数的概念。从本题的扇形统计图中，我们不能获取每个学生的等第这个精确数据，只能获取不同等第人数占总人数的百分比。由图可知，两个较高的等第A+和A的百分比之和为30%，两个较低的等第C和D的百分比之和为40%，比前者多了10%，而等第B的百分比是30%，故可以确定排在50%左右的成绩应为B等第。又因为不知道每个具体成绩出现的次数，所以不能确定这次考试成绩的众数。

解：（1）B。

（2）不一定。理由是：如果A+、A或D等第中某个分数出现次数最多，那么成绩的众数也可能被评定为A+、A或D等第。

【点评】寻找中位数的关键就在于找到“一半”位置的数据，寻找众数的关键在于知道出现次数最多的数据。有时即使没有精确的个体数据，也可以根据数据分布的情况获得答案。

二、通过数据分布感知方差的大小

例2甲、乙两人在相同的情况下各打靶10次，打靶的成绩如下图，这两人10次打靶平均命中环数都为7环，则______。（填“＞”“＜”或“=”）

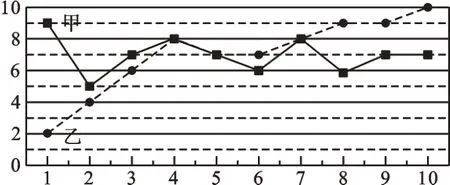
【分析】本题结合折线统计图考查方差的意义。折线统计图中的数据具体、精确，我们可以先计算出甲、乙两人打靶成绩的方差，再比较它们的大小。我们也可以由图中数据的分布情况，直观感受数据的波动程度，从而更加快捷地判断两人打靶成绩方差的大小。

解法1：根据方差公式计算，s甲2=1.2环2，s乙2=5.4环2，故填“＜”。

解法2：结合图形可以看出数据的分布情况，甲的10次成绩中有4次是平均数7环，而且其他数据也离7环不远，不难看出甲打靶的成绩数据比较稳定，波动较小，故填“＜”。

【点评】比较两种解法：解法1准确但计算量略大，解法2更便捷。结合折线统计图，有时我们可以很容易地看出两组数据波动的情况，凭直观就可以判断出两组数据的方差大小。当然，在有些问题中，由于几组数据的分布不易看出差异，那就只有具体计算出方差后，才能对各组数据波动的大小做出正确的判断。

一般地，我们利用平均数、中位数、众数来刻画数据分布的集中趋势，利用方差来刻画数据分布的离散程度。在学习这些知识的时候，我们不能仅局限于掌握统计量的简单计算，还要关注数据分布，把握统计量的本质，这样才有助于挖掘题中蕴含的隐形信息，快速解决问题。