基于相对业绩和惩罚机制的最优资产配置

殷子涵，董迎辉，王 磊

（苏州科技大学 数学科学学院，江苏 苏州 215009）

投资组合选择是金融的核心问题之一。投资组合理论主要研究投资者基于期望效用最大化原则的最优投资决策问题[1-4]。随着金融市场的发展，金融产品日益丰富，特别是基金产品发展迅猛，基金经理人的管理费机制也引起了学术界和业界的广泛关注，管理费机制对基金经理人的风险承担以及最优投资决策起着重要的影响。为了激励基金经理人，投资者通常会根据经理人的业绩支付一定的绩效费。激励机制会导致基金经理人为追求绩效费而采用过于冒险的策略从而伤害投资人的利益[5]，这是一个饱受争议的话题。文献[6]研究了在欧式看涨期权型绩效费机制下的最优投资问题，文中认为当基金价值低于期权型激励合约中预定的比较基准时，基金经理会大幅增加风险承担。沃伦·巴菲特认为绩效费合约是一种不公平的合约，因为经理人只分享投资收益而无需承担投资损失。文献[1]把惩罚机制考虑到了养老金的最优投资模型中，当基金账户的终端财富低于某比较基准时，养老金计划的经理人需要向养老金计划的参与人支付比较基准与终端财富之间的差额部分。

文献[5-6]均基于绝对业绩来制定基金经理的管理费方案。目前，金融业已经大量使用相对业绩评价方法来评价基金经理人的业绩水平并设立相应的管理费方案。投资者事先设立一个投资目标，该基准依赖于投资者的偏好，不同投资者所选择的基准是不同的。例如，我国广大的投资者希望投资收益率能够超过上证综指增长率或者通货膨胀率。文献[7]选择了某个随机基准，该基准可能是大盘指数或债券指数等，投资人同时考虑最大化终端绝对财富和相对财富的期望效用为目标来选择投资组合。文献[8]假设基金经理的管理费为相对业绩的非线性函数，他们研究了共同基金的相对业绩和风险承担之间的关系。

笔者受到文献[1]和文献[8]的启发，利用相对业绩评价法来评价基金经理的业绩，并把惩罚机制引入管理费方案，假设基金经理在收取固定管理费和与相对业绩成固定比例的可变管理费之和的同时，还面临着当相对业绩低于某一比较基准时，支付与比较基准和相对业绩的差额部分成固定比例的惩罚金。利用鞅方法求出了最优终端相对业绩的解析解。数值结果表明，当管理费中含有惩罚机制时，较高的固定管理费和较高的惩罚费有助于改进基金经理人的风险管理水平。

论文余下的结构安排如下：第一节阐述了基金经理人所面临的最优投资问题；第二节利用鞅方法求得了最优终端相对业绩的解析解；第三节进行了数值分析；第四节是结语。

1 基金经理人的最优投资问题

考虑一个[0，T]有限时间内的连续时间模型，假设市场上没有交易成本或税收。给定一个完备的概率空间（Ω，F，F，P），其中F:={Ft｜0≤t≤T}是由标准布朗运动{W（t）}0≤t≤T产生的满足通常条件的域流。

假设金融市场中存在两种可交易资产：无风险资产和风险资产。无风险资产的价格过程为

其中r＞0是无风险利率。风险资产的价格过程遵循几何布朗运动

其中μ＞r是风险资产的平均收益率，σ＞0为风险资产的波动率。

设基金账户的初始价值为x0≥0。令π（t）为投资于风险资产的财富比例，则财富过程Xπ（t）满足如下的随机微分方程

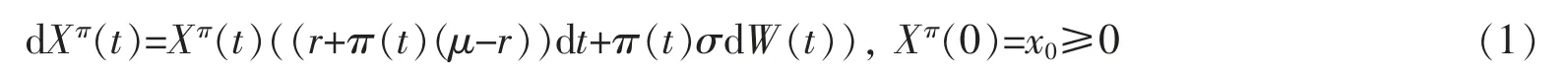
定义1如果对任意的几乎处处成立，并且式（1）存在唯一的解为

Xπ（t），那么投资组合策略π（t）称为是可允许的。记所有可允许的投资策略集为A。

假设基准资产的财富过程Y（t）满足

其中β＞0为投资于风险资产的财富比例。

令基于基准资产的相对业绩为

利用伊藤公式可以得到

其中δ（t）=π（t）-β称为跟踪误差。

假设基金经理人在T时刻收取的管理费为

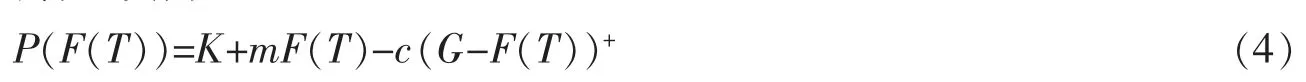
其中K，m，c≥0，且满足K-cG≥0。式（4）所给出的管理费方案意味着基金经理人在T时刻获得固定管理费K和与终端相对业绩F（T）成固定比例m的可变管理费的同时，如果终端相对业绩F（T）低于某预先给定的基准G时，还将支付金额为c（G-F（T））的罚金。基金经理人的目标是通过最大化其管理费的期望效用来寻找[0，T]内的最优投资策略。

文献[9-10]所提出的繁荣理论认为人们所做的投资决策与某个预先选择的参照点有关，当财富值高于参照点认为产生盈利，此时投资人表现为风险厌恶；当财富值低于参照点认为发生损失，此时投资人表现为损失厌恶。在数学上可以用一个S型的效用函数来刻画投资人的上述行为。类似于文献[11-12]，考虑如下的效用函数

其中0＜γ1＜1，0＜γ2＜1；B＞1衡量了基金经理人对损失的厌恶程度，θ是预先给定的基金经理人衡量其损益的参照点。

易见，当终端相对业绩F（T）不低于基准G时，基金经理人将获得不低于K+mG的管理费。惩罚机制的存在必然会促使基金经理人努力使得终端相对业绩高于基准G。所以，在文中，不妨假设θ≥K+mG，对于θ＜K+mG的情形，也可以利用文中所提出的方法类似讨论。

基金经理人的决策问题可表述为

因为市场是完备的，所以存在唯一的定价核

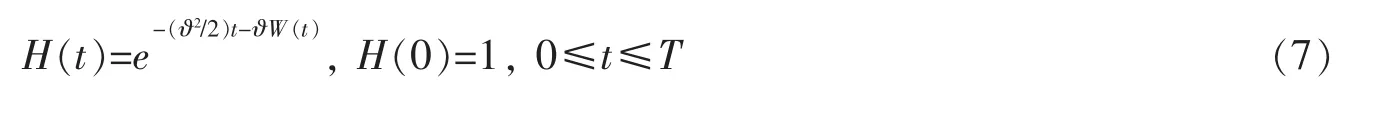
其中ϑ=（μ-r-σ2β）/σ。令

结合式（4）和式（5）可得

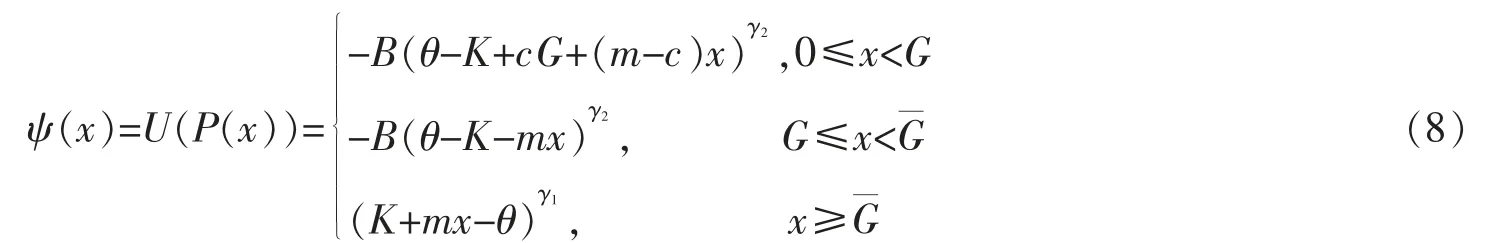
2 最优交易策略

在此节中，将求解最优化问题，并推导出基于相对业绩和惩罚机制下的最优终端相对业绩。

为了简化公式，记

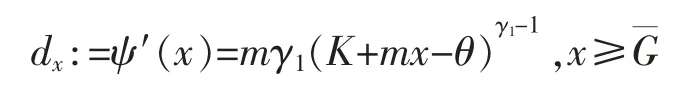
令

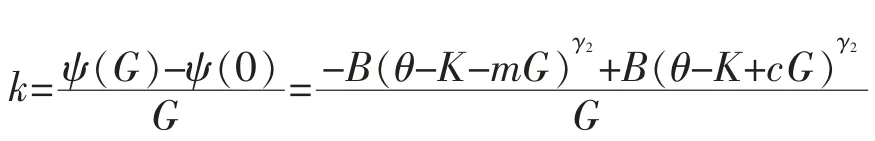
为过点（0，ψ（0））与（G，ψ（G））所作直线的斜率。

类似于文献[1]，将采用凸对偶方法来解决问题（9），首先利用凹化方法来找出

的最大值点x*（y）。

引理1方程

证明令f（x）=ψ（x）-ψ（G）-（x-G）dx。易证f（x）在（，+∞）上是单调递增的连续函数，并且因此，方程（11）存在唯一的解z1＞G¯。

命题1令ψ（x）由式（8）所定义，z1是方程（11）的唯一解，则ψ（x）的凹包络ψc（x）为：

情形一：当k＜dz1时，

其中z0是下列方程

情形二：当k≥dz1时，

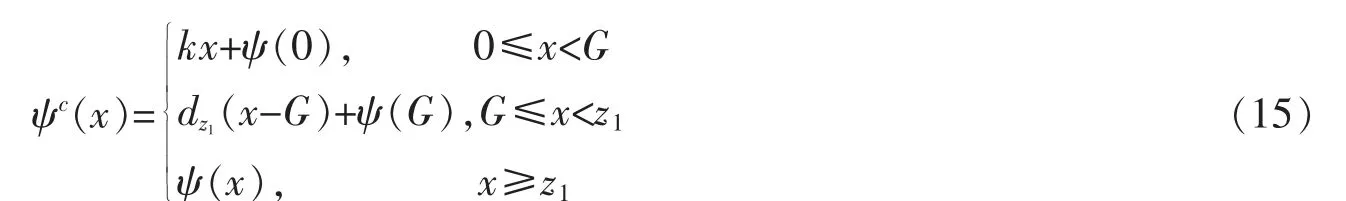
对于固定的y＞0，最大值问题（10）的最大值点为

证明比较k与dz1的大小，需分两种情形来讨论。

情形一：当k＜dz1时，过点（0，ψ（0））作曲线ψ（x）的切线，易证，存在唯一的切点，记为z0。注意到，对于所有的0≤x≤z0，都有ψ（x）≤dz0x+ψ（0）成立。由文献[13]的引理A1可知，ψ（x）的凹包络由式（12）给出（如图1所示）。 对于固定的y＞0，式（10）的最大值点

图1 当k＜dz1时，ψc（x）及ψ（x）的图像

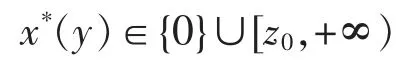
应为式（14）所给出的使得ψc（x）-xy的超微分为0的点。

情形二：当k≥dz1时，利用文献[13]中的引理A1便可得到的凹包络由式（15）给出（如图2所示）。类似于情形一中的推导不难得到，式（10）的最大值点由式（16）所给出。

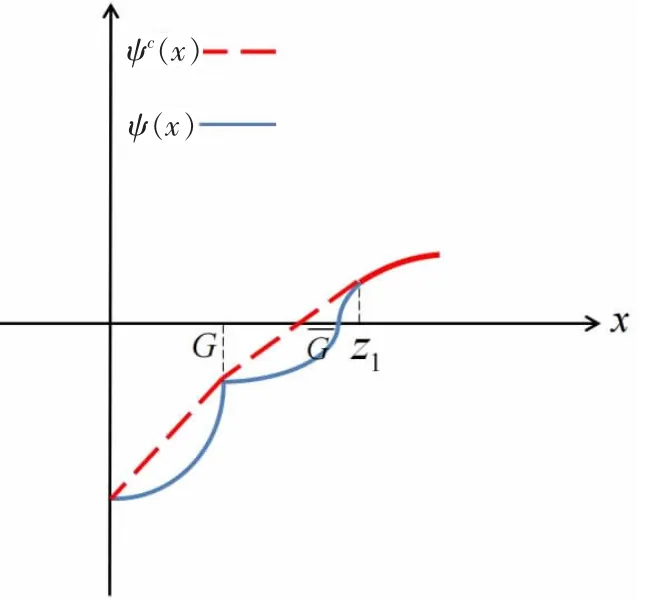
图2 当k≥dz1时，ψc（x）及ψ（x）的图像

命题2令z1是方程（11）的唯一解。则优化问题（9）的最优终端相对业绩，记为Fπ*，λ*（T），有如下的表达式，其中的拉格朗日乘子λ*＞0满足E[H（T）Fπ*，λ*（T）]=1：

情形一：当k＜dz1时

情形二：当k≥dz1时

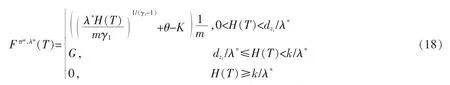
证明类似于文献[1]，运用凸对偶原理，首先对固定的拉格朗日乘子λ＞0，求解问题

对固定的λ＞0，式（19）的最优解，记为Fπ*，λ（T），可表示为

其中x*（·）由式（14）和式（16）给出。再利用互补松弛条件，通过求解预算方程

求出拉格朗日乘子λ*立得结论。

利用命题2，便可求出时刻最优相对业绩Fπ*，λ*（t）的解析解。注意到H（t）Fπ*，λ*（t）是一个鞅。 因此，

将式（17）和式（18）代入上式计算条件期望便可得到Fπ*，λ*（t）。一旦求出Fπ*，λ*（t），只需对其运用伊藤公式并与式（3）比较，就可以得到最优投资比例的解析解。在求出最优投资策略后，就可以数值分析惩罚机制对基金经理人投资决策的影响，从而为薪酬方案的设立提供一些理论依据。出于篇幅的考虑，这里没有给出t时刻最优相对业绩和最优投资比例的具体表达式。

3 数值分析

此节将给出一些数值算例来阐述管理费机制对最优终端相对财富的影响。 除非特别声明，设定参数值：r=0.03，μ=0.07，σ=0.2，x0=100，T=1，B=1.5，m=0.4，θ=2，β=0.6，γ1=γ2=0.5，G=0.8。

图3刻画了对不同的固定费用K，最优终端相对业绩Fπ*，λ*（T）与H（T）的关系。由图中可以看出，当固定管理费较高时，在经济状况较好时，最优终端相对业绩Fπ*，λ*（T）较低，但当经济萧条时，Fπ*，λ*（T）的尾部风险也较低。这是因为如果经济萧条时，基金经理人经营业绩不佳将会受到惩罚支付，所以较高的固定管理费会使得基金经理为了减少受到惩罚的可能性而降低对风险资产的投资，从而减小最优终端相对业绩Fπ*，λ*（T）的波动性。

图3 对不同的K，Fπ*，λ*（T）与H（T）的关系

图4描绘了对不同的c，最优终端相对业绩Fπ*，λ*（T）与H（T）的关系。可以看出，当c较高时，在经济状况较好时，最优终端相对业绩Fπ*，λ*（T）较低。因为较高的c意味着在经济萧条时，当基金经理人投资业绩不好时将会受到较高的惩罚，所以经理人会降低对风险资产的投资，从而导致在经济繁荣时较低的最优终端相对业绩Fπ*，λ*（T）。

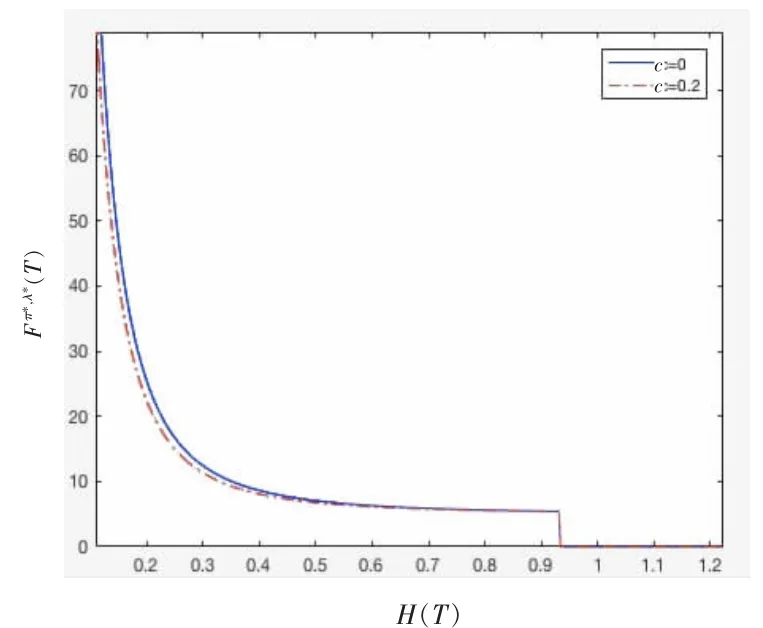
图4 对不同的c，Fπ*，λ*（T）与H（T）的关系

4 结语

基于相对业绩，在带有惩罚机制的管理费方案下研究基金经理人以最大化其管理费的期望效用为目标的最优投资组合选择问题。首先，找到了市场中唯一的定价核，从而可以把动态的优化问题转化为静态的终端最大化问题；然后，用鞅方法给出了最优终端相对业绩的解析解；最后，数值计算表明文中所考虑的基于相对业绩评价法下的带固定管理费和惩罚机制的管理费方案，能从一定程度上改进基金经理人的风险管理。