具有多领导的Cucker-Smale模型的有限时间集群运动行为
2022-11-28杨施丹尤希舟茹立宁
杨施丹,尤希舟,王 俊,茹立宁*
(1.苏州科技大学 数学科学学院,江苏 苏州 215009;2.江苏科技大学 理学院,江苏 镇江 212003)
最近20年内,自组织粒子群的集群运动行为引起各个领域专家的兴趣,尤其是生物、物理、控制以及数学等领域[1-8]。集群运动行为是指鸟群、鱼群等生物群体只使用有限的环境信息和简单的通信规则,经过一段时间运动,最后实现速度同步。在描述上述运动的模型中,文中研究由Cucker教授和Smale教授创建的模型[9-10]:每个个体通过其他个体的影响作用来调整自己的速度。在Cucker-Smale(C-S)模型中,存在一个非常重要的衰减指数β:当0≤β≤1/2时[11-12],无条件集群运动发生;而当β>1/2时[9-10],条件集群运动发生,且发生条件仅依赖于初值与模型参数。
C-S模型的新颖性与有趣性吸引了大量学者的注意力。受鸟群迁徙启发,Shen[13]把等级结构引入C-S模型,该模型所对应的Laplace矩阵是下三角矩阵。Li等人[14]利用(sp)矩阵研究了根领导下的C-S模型。Dong等人[15]进一步研究了一般有向图下的C-S模型,该模型是上述两种模型的推广。受这些模型的影响,刘友权等人[16]研究了仅有一个领导者的一维与多维C-S模型在有限时间内发生集群运动行为的问题。需要注意的是,文献[16]假设影响函数具有下界,弱化了研究问题的难度。基于此,文中研究具有多领导的多维C-S模型在有限时间内发生集群运动行为的问题。相较于仅有一个领导者的模型而言,首先,需要克服由多领导者的相互耦合所造成的研究难点,利用文献[17]的定理3.1,可以得到领导者在有限时间内发生集群运动行为,不妨设发生时刻为T1,因此在T1时刻后,领导者的速度相同;然后,把C-S模型转成一个新的误差模型,利用能量方法并构造Lyapunov函数研究该模型;最后,回归原始模型,得到系统在有限时间内发生集群运动行为。
1 预备知识
研究具有多领导的Cucker-Smale模型:考虑由N+M个个体组成的系统,其中个体N+1,N+2,…,N+M是领导者,个体1,2,…,N是跟随者。
对于M个领导者而言,满足如下模型

对于N个跟随者而言,满足如下模型

在系统(1)-(2)中,xi∈Rd,vi∈Rd分别表示个体i的位移和速度,α>0是一个正常数。影响函数ψ是非负非增函数,具体表达式为:ψ(s)=1/(1+s2)β(β≥0)。||·||是l2-范数,即对于y=(y1,y2,…,yd)T∈Rd,有函数sig(y)θ=(sgn(y1)|y1|θ,sgn(y2)|y2|θ,…,sgn(yd)|yd|θ)T,其中,sgn:R→{-1,0,1}为符号函数,常数0<θ<1。
注:一方面,文中研究的多领导-多跟随者系统来源于文献[18]的3.2节“Flocking with multiple leaders”,多领导模型的具体定义见文献[18]的定义3.4。笼统地说,领导者仅受其他领导者的影响,而跟随者受跟随者以及领导者的影响。另一方面,对于一般有向图下的C-S模型,且该有向图含有生成树而言[15],多领导-多跟随C-S模型是其特例。这是因为在系统(1)-(2)所对应的邻接图中,每个领导者都可以看成一个根,对其他领导者以及跟随者产生影响,从而该邻接图有M个生成树。综上所述,文中研究的模型是合理有效的。
C-S模型在有限时间内发生集群运动行为的定义如下:
定义1如果系统(1)和(2)满足如下两个条件,则称该系统在有限时间内发生集群运动行为:
(1)速度的波动在有限时间内等于0:对于任意t≥T0,有||vi(t)-vj(t)||=0,1≤i,j≤N,其中T0=inf{T:||vi(t)-vj(t)||=0,∀t≥T}被称为收敛时间。
下面的两个引理在定理的证明中起到非常重要的作用。
引理1[19-20]设a1,a2,…,an是非负实数,若0<r<s,则
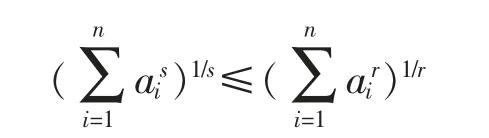
引理2[20-21]若可微函数V(t):[0,+∞)→[0,+∞)满足微分不等式

其中c>0,0<θ<1,则对于任意给定的时刻t0≥0,V(t)满足如下不等式:V(t)≤(V(t0)1-θ-c(1-θ)t)1/(1-θ),t0≤t≤t1,以及对于t≥t1,V(t)≡0,其中t1≤t0+V(t0)1-θ/c(1-θ)。
2 主要结论
为了研究系统(1)-(2)在有限时间内发生集群运动行为,首先研究领导模型(1)的集群运动行为。引入系统(1)的平均位移和平均速度(xc,vc),即显然,。根据文献[16]的定理3.1:当t≥T1时,系统(1)的M个领导者发生集群运动行为,且


当t≥T1时,考虑如下的误差系统,系统(1)可转化为

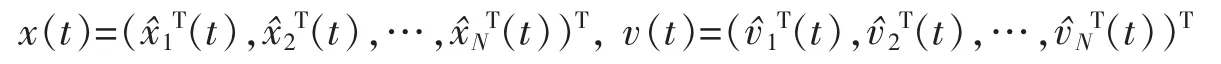

引理3设是系统(1)-(2)的解,则当t≥T1时,||x(t)||,||v(t)||满足如下不等式

证明(1)类似于文献[8],仅考虑||x(t)||≠0的情形,有
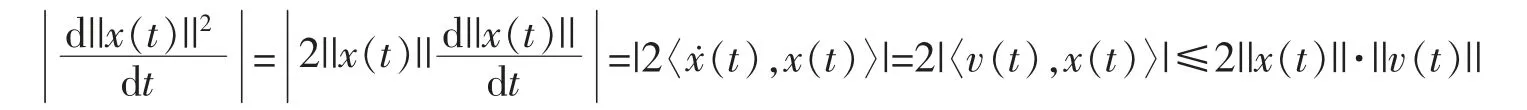
(2)考虑||v(t)||2,对其求导,得

根据ψij=ψji以及符号函数的性质,有

类似于I1的推导

由公式(6)以及ψ的非增性可知ψij≥ψ(a+||x||)。从而代入上式,有

又由于0<θ<1,即1<θ+1<2,由引理1知
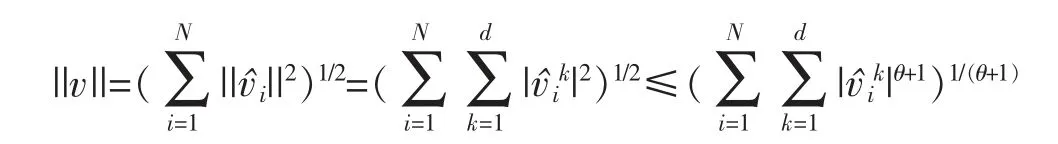
整理得
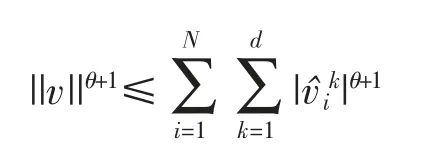
所以,代入式(9)得
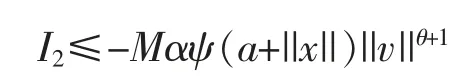
因此,


引理4若T1时刻的速度和位移满足下式

则系统(1)-(2)在有限时间内发生集群运动行为。确切地说,存在非负常数xM,当t≥T1时
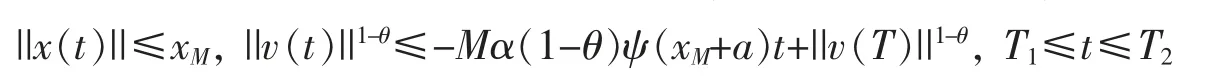
以及v(t)≡0,t≥T2,其中
证明构造Lyapunov函数

由引理3可得
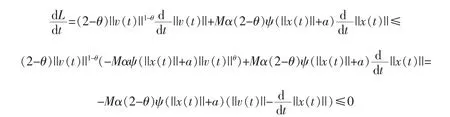
故L(t)是非增函数,从而当t≥T1时,L(t)≤L(T1),即
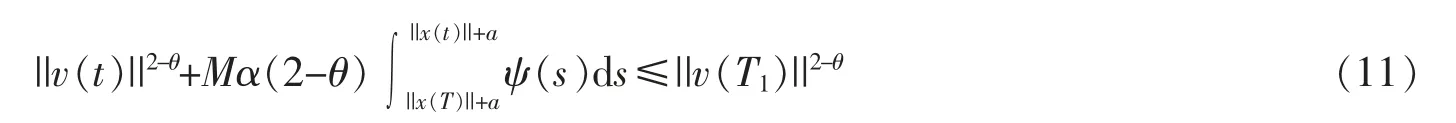
由已知条件(10)以及ψ的非增性知,存在xM≥||x(T1)||,使得
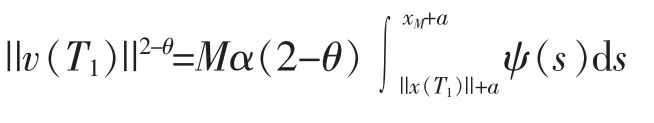
代入式(11)得
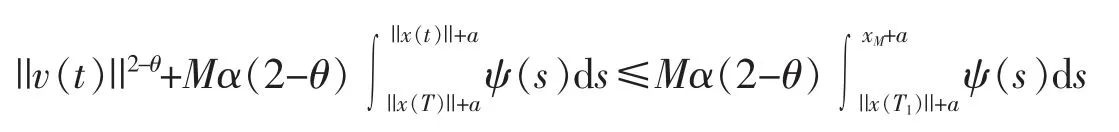
进一步,有
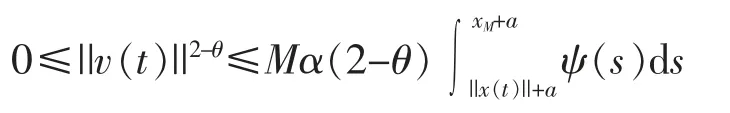
再由ψ(s)的非负性知

由ψ(s)是减函数,可得ψ(xM+a)≤ψ(||x(t)||+a)代入引理3的式(8),有

由引理2知
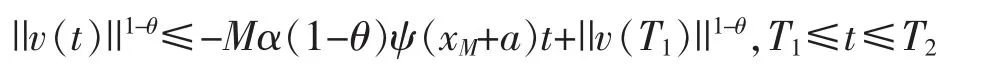
以及当t≥T2时,||v(t)||≡0,其中。由定义1知,系统(2)在有限时间内发生集群运动行为,从而系统(1)-(2)也在有限时间内发生集群运动行为。
依赖前面的引理,有如下的定理成立。
定理1对于系统(1)-(2)来说,若以下条件成立之一:(1)0≤β≤1/2;(2)β>1/2且
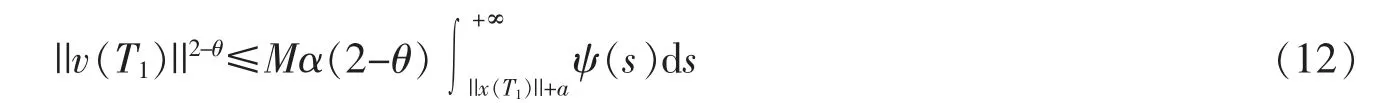
则集群运动行为在有限时间内发生。
证明一方面,若0≤β≤1/2,有,满足引理4的条件;另一方面,当β>1/2时,由条件(12)知初始位移及速度满足引理4。综上,由引理4知,系统在有限时间内发生集群运动行为。
3 结语
利用误差模型,研究了具有多领导的C-S模型的有限时间集群运动行为问题,并得到在有限时间内发生无条件集群运动行为和条件集群运动行为。对于发生集群运动行为的有限时间的上界估计是未来的研究内容。
