高应变率下含水红砂岩爆破损伤演化模型研究

柴耀光，刘连生,2，曾 鹏，刘 伟，易文华，杨 砚，钟抒亮,陶铁军,3

(1.江西理工大学资源与环境工程学院，江西 赣州 341000; 2.江西省矿业工程重点实验室，江西 赣州 341000; 3.贵州大学土木工程学院，贵阳 550000)

近年来，爆破技术因其高效性而被广泛应用于矿山开采、隧道开挖、地下工程等领域[1-2]。得益于此，地下工程及开采作业逐渐向深部进行。自然条件下，岩体大多处于含水状态[3]，岩体的力学性能受水的影响很大，含水量的微小变化可能会导致岩石强度与变形能力的显著变化。地下工程爆破开挖时，不可避免的会遇到含水岩体，轻易忽略爆破冲击对含水岩体的损伤影响，可能会引发重大安全事故。因此，为探究含水岩体在爆破冲击作用下的损伤演化规律，有必要建立相应的损伤本构方程。

国内外学者[4-9]研究发现，既使是岩性不同的岩样，其力学特性也往往随着含水率的升高而逐渐劣化：岩石颗粒与水之间的水-岩交互作用受矿物组成、粒径、孔隙体积等结构的影响较大，不同岩石类型之间差异较明显。损伤本构模型作为描述岩石破坏过程的有效工具而被众多学者[10-12]所推崇，与此同时，考虑复杂载荷或环境条件下的岩石静载损伤模型已经引起了许多研究人员[13-16]的注意，并取得了丰富的研究成果。在此基础上Li等[17]、Qiao等[18]、Dong等[19]、Suzuki等[20]对于岩石动态本构方程也进行了详细的探究，王聪聪等[21]基于断裂力学建立了含水裂纹在爆破扰动下的力学模型。然而，却很少有研究涉及含水率和应变率耦合作用下岩石的动态损伤本构方程。含水红砂岩在动载作用下其损伤可以分为两部分：一是水对岩体力学性能的劣化引起的宏观损伤；二是动荷载冲击对岩体内部裂隙等所造成的微观损伤；因此可从宏观与微观两方面探究其动载作用下所受复合损伤。针对不同含水率的红砂岩试样，岩石内部损伤随着含水率的增加而逐渐扩大，表现为岩体弹性模量、内摩擦角、粘聚力等参数的降低，其中岩体弹性模量常用来表征岩体的损伤[22-23]。因此考虑用弹性模量定义红砂岩的含水损伤；荷载作用下，岩体内部微元破坏数量与其所受荷载大小呈正相关关系，可用微元体破坏数量来定义荷载损伤。为了准确描述含水率和应变率耦合作用下岩石的本构方程，本文考虑将岩石损伤等效为两部分：不同含水率造成的宏观损伤以及不同应变率作用导致的微观损伤，进而提出一个可以综合反映含水率和应变率耦合作用下的红砂岩动态损伤本构方程。

本文通过对含水红砂岩进行动态冲击试验。基于Weibull分布与Drucker-Prager准则，推导得到红砂岩在含水率与应变率耦合作用下的复合损伤变量与动态损伤本构方程，并将本构方程推导的理论曲线与试验所得进行对比，拟合度较好。

1 试验

1.1 试样制备

试验所用红砂岩由江西赣州采集，由石英、长石、云母等矿物组成。按ISRM[24]建议，切割成直径50 mm长径比1∶1的圆柱体。通过测量试样孔隙度、质量、纵波波速等，剔除离散性较大试样。将制备好的红砂岩置于实验室通风1个月，得到完全干燥试样。部分制备好的试样如图1所示。

图1 部分试样

为得到不同含水率的试样，将加工好的试样置入盛满水的水箱中，间隔1 h取出进行称重，直到试样重量不变为止，认为此时试样已饱和。根据其重量的变化可确定试样含水率，公式如下：

(1)

式中：ω为岩石含水率;Ww为含水岩石质量;Ws为干燥岩石质量。

经试验，不同含水率的试样可通过控制浸水时间得到。本试验设计5种含水率，分别为0%、0.75%、1.5%、2.25%、3.0%。不同含水率试样制备过程如表1所示。

表1 不同含水率试样制备

1.2 仪器简介

冲击试验在霍普金森压杆[25]上进行。装置冲头与杆件由40 Cr合金钢制成，密度为7 810 kg/m3; 纵波波速为5 400 m/s；弹性极限为800 MPa；入射杆、透射杆与缓冲杆的长度分别为2.0、1.5、0.5 m。为确保所得试验数据的有效性，每次冲击后进行动态应力平衡检验(见图2)。直径50 mm的SHPB试验系统如图3所示。

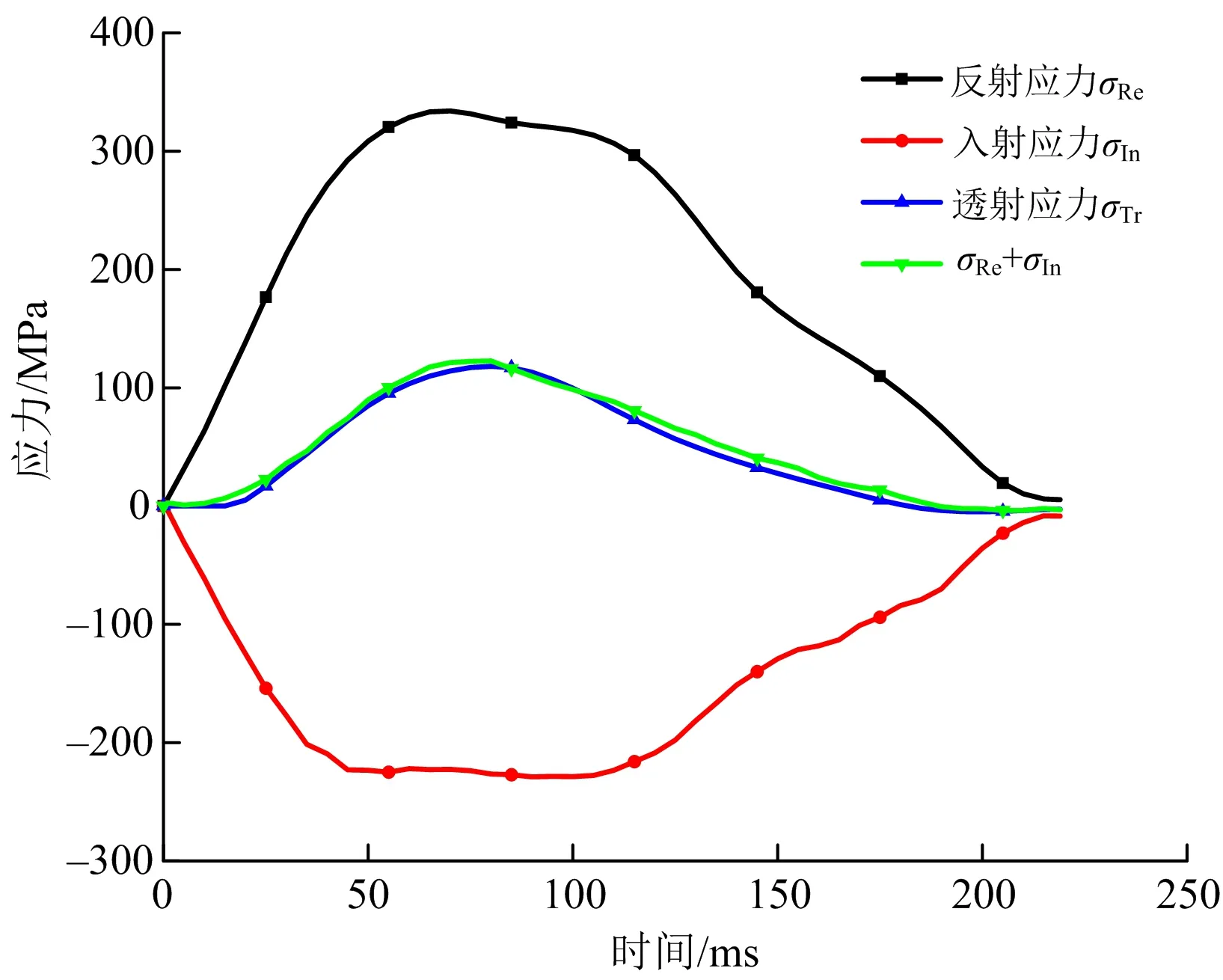
图2 试样N-5-5动态应力平衡

图3 SHPB试验系统

1.3 试验方案

为探究高应变率下含水红砂岩的复合损伤变量与动态损伤方程，试验分设5种不同的含水率与应变率，对其组合分析。试验分为5组，以N为编号，后接不同的数字组合进分组。以N-1-1为例，中间的数字范围由1～5，代表了由低到高的5种应变率。而末尾的数字同样由1～5，代表由低到高的5种含水率。每组试验重复3次，由于数据过多，每组试验仅列出1组试验结果，部分试验数据如表2所示，其变化规律如图4所示。

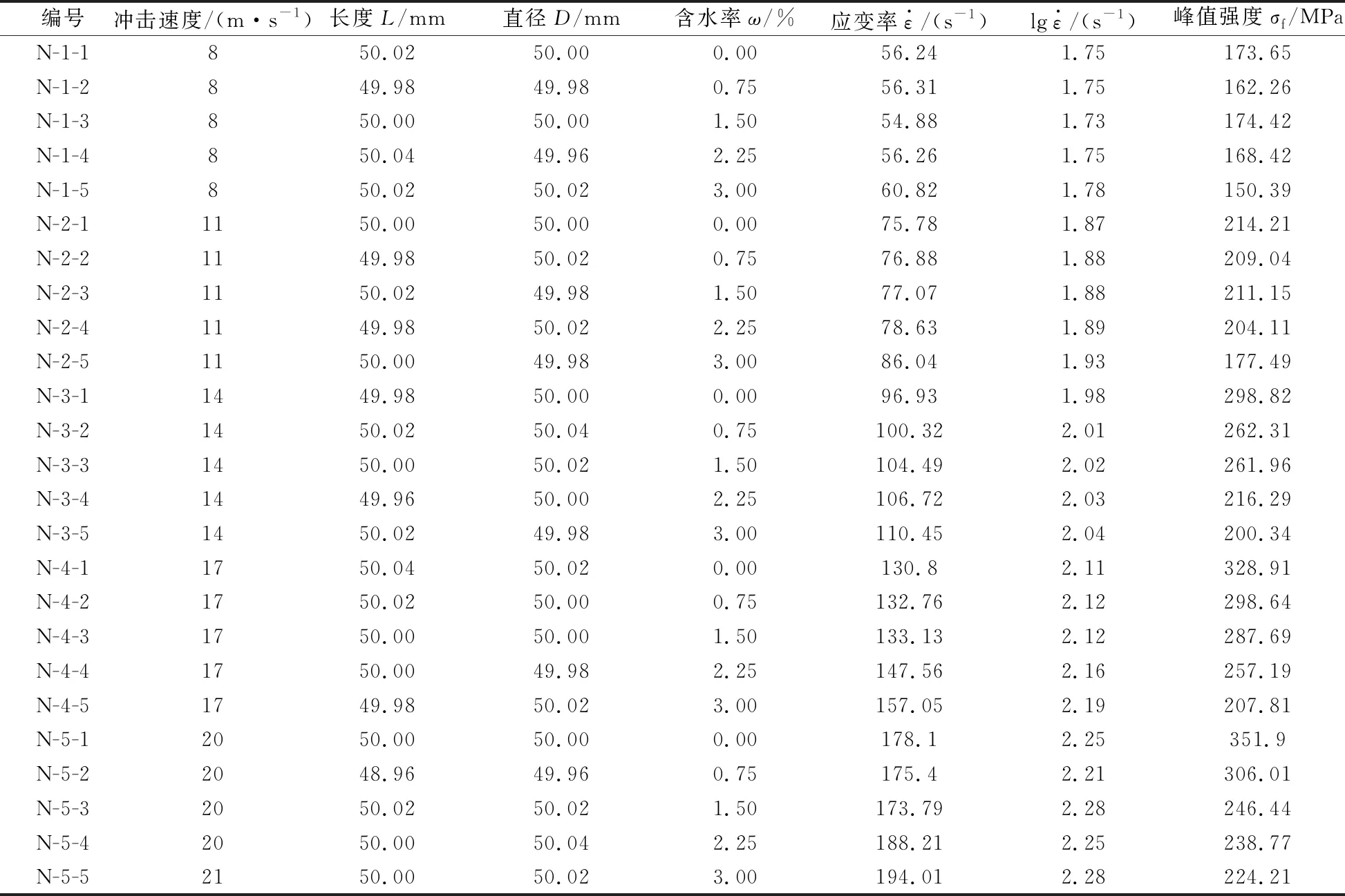
表2 红砂岩动态压缩试验结果

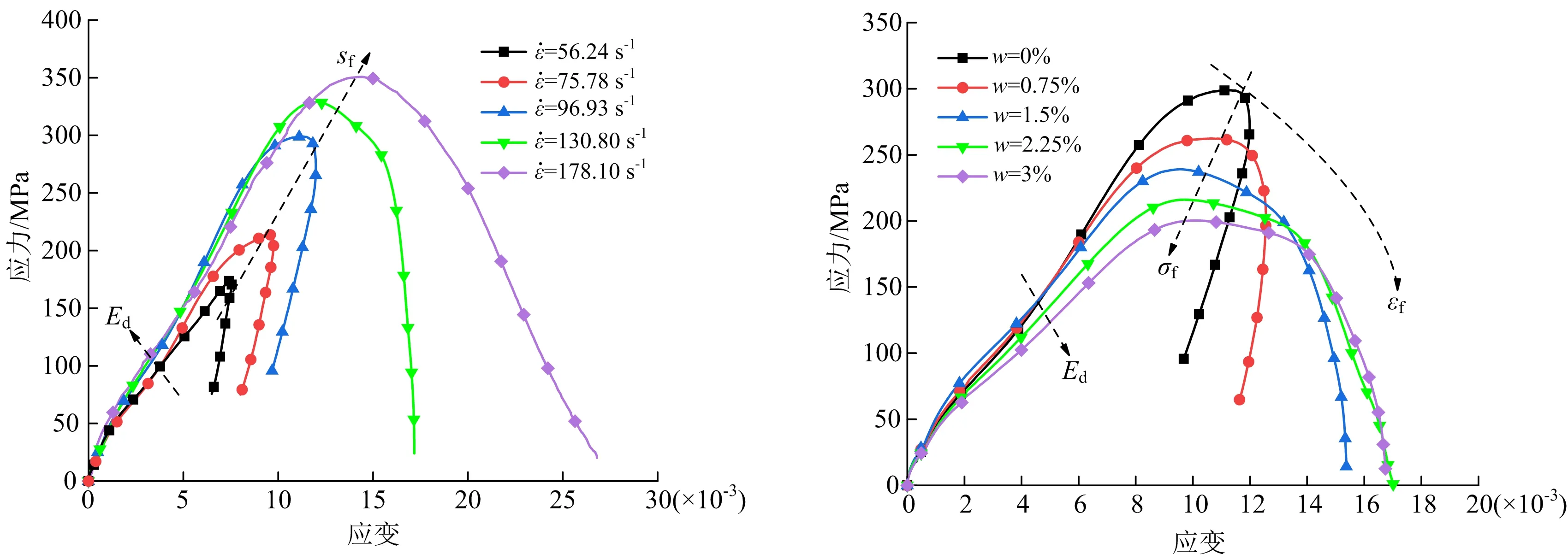
图4 红砂岩动态应力-应变

由图4可知，随着含水率的增加，试样的动态弹性模量逐渐减小，峰值应力对应的破坏应变逐渐降低，临界应变逐渐变大；试样在破坏后，应力-应变曲线并非直线下降, 而是应力缓慢下降至临界应变处后迅速破坏，即随着含水率的增加，试样逐渐由脆性向延性转化。相同应变率下，试样的峰值应力随含水率的增加而降低。

2 红砂岩损伤演化方程

2.1 含水状态下红砂岩损伤演化方程

本文所采用的损伤变量由宏观与微观两部分组成，微观损伤可由裂隙数目、缺陷体积等来定义；宏观方面可以用波速、能量、密度、波阻抗、弹性模量等来定义；在含水率和应变率的共同影响下，岩石的损伤不仅表现在微观结构上，而且在力学性能上也有不同程度的劣化。含水率越高，水对岩体所造成的宏观损伤就会越大，弹性模量下降越多。因此可用弹性模量来定义岩体含水损伤，表达式为

(2)

式中：D1为含水率损伤变量；Eω为不同含水率岩石的弹性模量；E0为干燥状态下岩石的弹性模量。

2.2 荷载作用下红砂岩损伤演化方程

目前，正态分布与Weibull分布是最常用的2种岩石微元强度分布方式。第1种分布方式可以较好的描述岩石内部损伤的演化且物理意义较为明确，但是计算过程过于复杂，实际应用较少。第2种基于Weibull理论的分布方式却具有计算量小、描述准确等优点，因此被更多的学者所采用。其表达式如下：

(3)

p(F)=0(F≤0)

(4)

式中：m、F0为Weibull分布参数。

岩体受荷时，其内部微元体破坏数量增加，当破坏数量达到极限时，会引起岩体的宏观破坏。因此，荷载损伤变量可以用微元体破坏数量来衡量，即：

(5)

式中：D2为荷载作用损伤变量；Nn为已破坏的微元体数目；N为总的微元体数目。

当岩体所受外荷载由0增长到F时，其内部微元体破坏数目可由下式进行计算：

(6)

将式(6)代入式(5)，可求得荷载损伤变量：

(7)

微元体受荷时的损伤本构方程可根据等效应变假设求得：

(8)

从式(7)可以看出，荷载损伤变量D2与微元体的强度F有关。Drucker-Prager准则(以下简称D-P准则)因比其他理论更能反映岩体的实际情况而被广泛应用。本文认为红砂岩的破坏服从D-P准则[26-27]。

(9)

式中：φ为岩石的内摩擦角;I1 ,J2为应力张量的第一不变量和应力偏量的第二不变量。

基于D-P准则，曹文贵等[28]确定了在三轴压缩条件下岩石的I1与J2的表达式：

(10)

(11)

式中：v为试样的泊松比；E为试样的初始弹性模量；ε1为试样的轴向应变。

动态单轴压缩下，试样的σ2=σ3=0，ε1=ε。式(10)、式(11)可转化为

I1=Eε

(12)

(13)

把式(12)、式(13)代入式(9)中可得：

(14)

对式(8)、式(14)求导可得：

(15)

(16)

当试样的应变达到临界应变，即ε=εf时，由函数在极值点处导数为零可得：

(17)

联立式(15)、式(16)、式(17)可得：

(18)

(19)

岩石在临界破坏即ε=εf时，σ=σf，此时把式(19)代入式(8)中可得：

(20)

把式(20)代入式(7)，可得岩石受荷载作用时的损伤变量表达式：

(21)

2.3 复合损伤变量的演化方程

含水率以及荷载作用均会对岩石试样产生不同的损伤，根据损伤力学理论，岩石的损伤变量可以用宏观物理指标如弹性模量表示。表达式如下：

(22)

式中：Dω为复合损伤变量;Eω为含水率和荷载作用下岩石弹性模量;E0为初始弹性模量。

岩石在单轴加载下的应力-应变关系可根据等效应变原理求得，如下：

(23)

式中：σ,E为未损坏材料的应力和弹性模量；σ*,E*为损坏材料的有效应力和相应的弹性模量；ε,D分别为材料的应变和损伤变量。

岩石在含水率与荷载共同作用下的本构关系如下：

σ=E0(1-Dω)ε

(24)

式(24)中Dω可表述为

Dω=D1+D2-D1D2

(25)

从式(25)可知，岩体的整体损伤变量Dω由含水损伤D1和荷载损伤D2以及它们之间的耦合相互作用组成。因此，损伤变量呈现典型的非线性特征。此外，由于耦合项整体为负，说明含水率和应变率的耦合效应实际上削弱了岩石的总体损伤。

综上，单轴压缩下含水岩体的损伤本构方程为

σ=E0[1-(D1+D2-D1D2)]ε

(26)

上述所说荷载损伤为静态荷载下岩石的损伤,对于动态压缩下，由于岩石率效应的影响，试样所受的应变率越大，其弹性模量、临界应变就会越来越大。考虑到应变率的影响，将荷载损伤变量D2看作为应变率有关量，即D2中的参数均视为应变率相关量。从式(21)可以看出，与荷载损伤变量有关的岩石宏观物理指标有峰值应力、临界应变和弹性模量，因此动态压缩下岩石荷载损伤变量D2的计算方式是以干燥红砂岩试样的动态压缩试验为基础，根据试验所得的不同应变率下的峰值应力、临界应变、弹性模量等参数，绘制出相应的散点图并进行拟合，进而得到岩石宏观物理参数的率效应模型，并将其与含水损伤变量共同代入式(25)可得到含水率和应变率共同作用下的复合损伤变量。

3 损伤变量的确定

3.1 含水损伤变量

D1可由含水红砂岩的静态弹性模量代入式(2)求得，计算结果如表3所示，变化规律如图5所示。

表3 D1随含水率的变化规律

图5 D1随含水率变化

D1整体的变化近似呈指数函数增长。方程如下：

D1=-0.709e(-ω/3.113)+0.706 (R2=0.99)

(27)

由图5可知，D1随含水率的增加而逐渐增大。这是因为随着岩体内部水分增加，更多的岩体开始遭受水岩作用，造成的损伤逐渐变大。由曲线斜率可知，D1增长的趋势逐渐减小，这是由于随着水分不断进入试样内部，试样逐渐饱和，水-岩耦合作用逐渐达到平衡，损伤的增加也在逐渐减小。

3.2 荷载损伤变量

根据式(20)，在含水率为0的情况下，选取不同应变率下的损伤变量来计算所需的弹性模量、峰值应力等参数,用于计算荷载损伤的m值。得应变率作用下m的变化曲线(见图6)。由图6可以看出，m与应变率两者之间近似呈线性关系，m随着应变率的增加而逐渐增大，表达式如下：

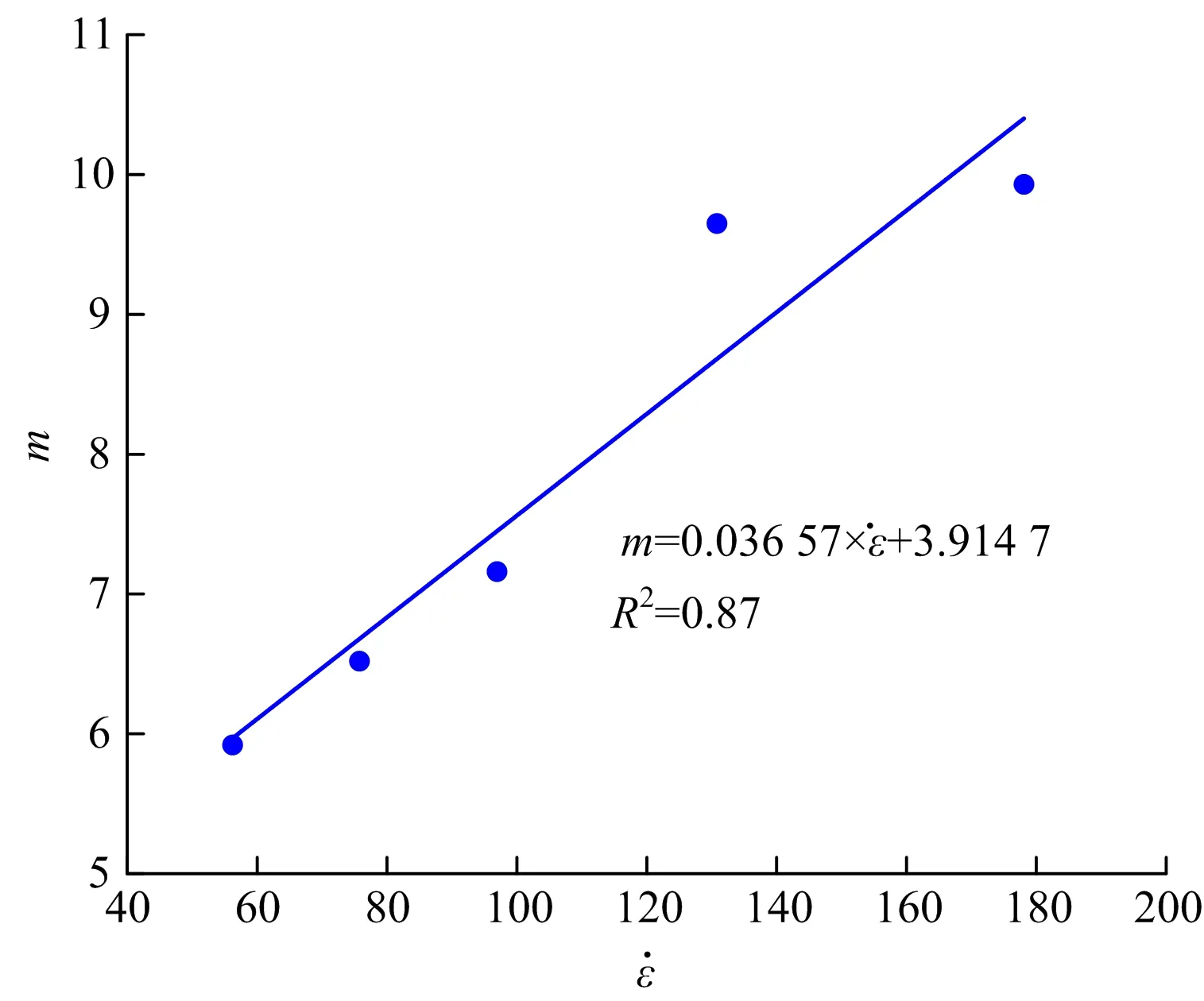
图6 m值随应变率变化

(28)

把计算好的m值代入到式(21)中可得荷载损伤D2随应变的变化曲线(见图7)。

图7 D2随应变变化

由图7可知，冲击作用下，荷载损伤D2的增长过程可分为3部分，即初始阶段、低速发展阶段和快速发展阶段。初始阶段，岩体瞬间遭受动荷载作用，内部孔隙、裂纹等闭合，荷载损伤量迅速增加，并随着应变率的增加而扩大。但此阶段作用于岩体上的应变率，并不足以使岩体内部产生新的裂纹，所以其荷载损伤量趋于稳定。对应于岩石动态压缩过程中的压密阶段；低速发展阶段，荷载损伤增长几乎为0，对应于岩石压缩过程中的弹性阶段与微裂纹稳定扩展阶段，此阶段裂纹增加缓慢，损伤变量变化较小；快速发展阶段，损伤快速增长，对应于岩石裂纹快速扩展与破坏阶段，岩石内部产生大量裂隙，并迅速贯通，损伤快速增加，直至岩石完全破坏。

3.3 复合损伤变量

根据得到的含水损伤变量D1和荷载损伤变量D2的变化规律，计算D1、D2的值并代入式(25)中，可以得到含水率和应变率共同影响下的复合损伤变量Dω的变化趋势。应变率为96.93 s-1时，不同含水率下复合损伤Dω的变化如图8所示。

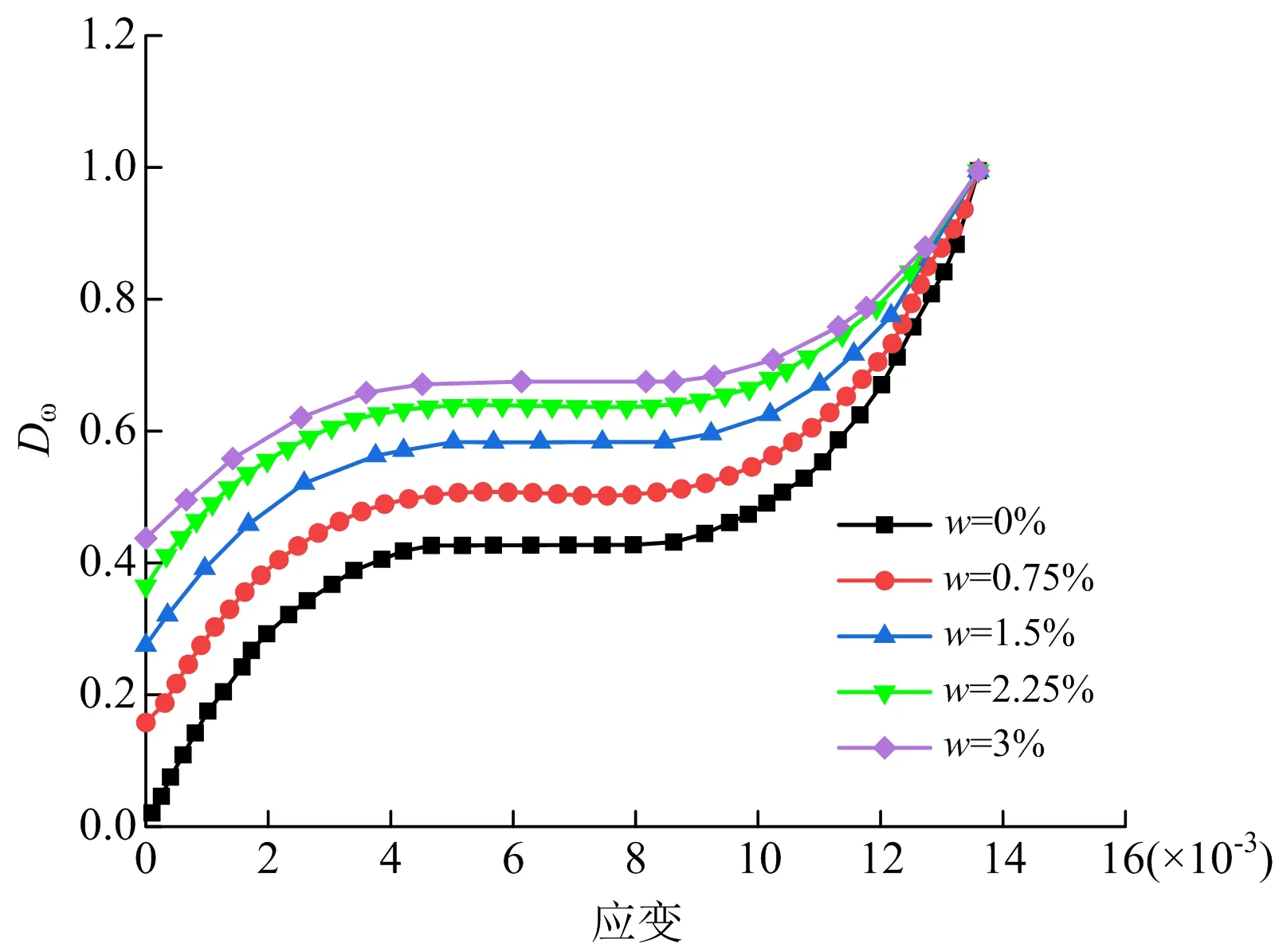
图8 Dω随应变变化

由图8可知，复合损伤变量Dω与荷载损伤D2的变化趋势近似，不同的是在中期复合损伤变量Dω的变化相较于荷载损伤D2较为缓和。这是由于在裂纹加速扩展阶段，由于水Stefan效应[29]的影响，会阻止裂纹的快速扩展，进而导致复合损伤Dω在加速阶段的变化较为缓和。

由图8可知，当应变为0时，此时的复合损伤变量Dω仅代表含水损伤。且含水率越大时，Dω的初值越大，岩石的初始含水损伤越严重。

4 红砂岩动态损伤本构模型验证

为验证理论推导所得红砂岩动态损伤本构模型的准确性，将计算好的复合损伤变量代入式(26)中，可得到红砂岩理论应力-应变曲线。通过对比实测曲线可对本构模型的准确性进行验证(见图9)。

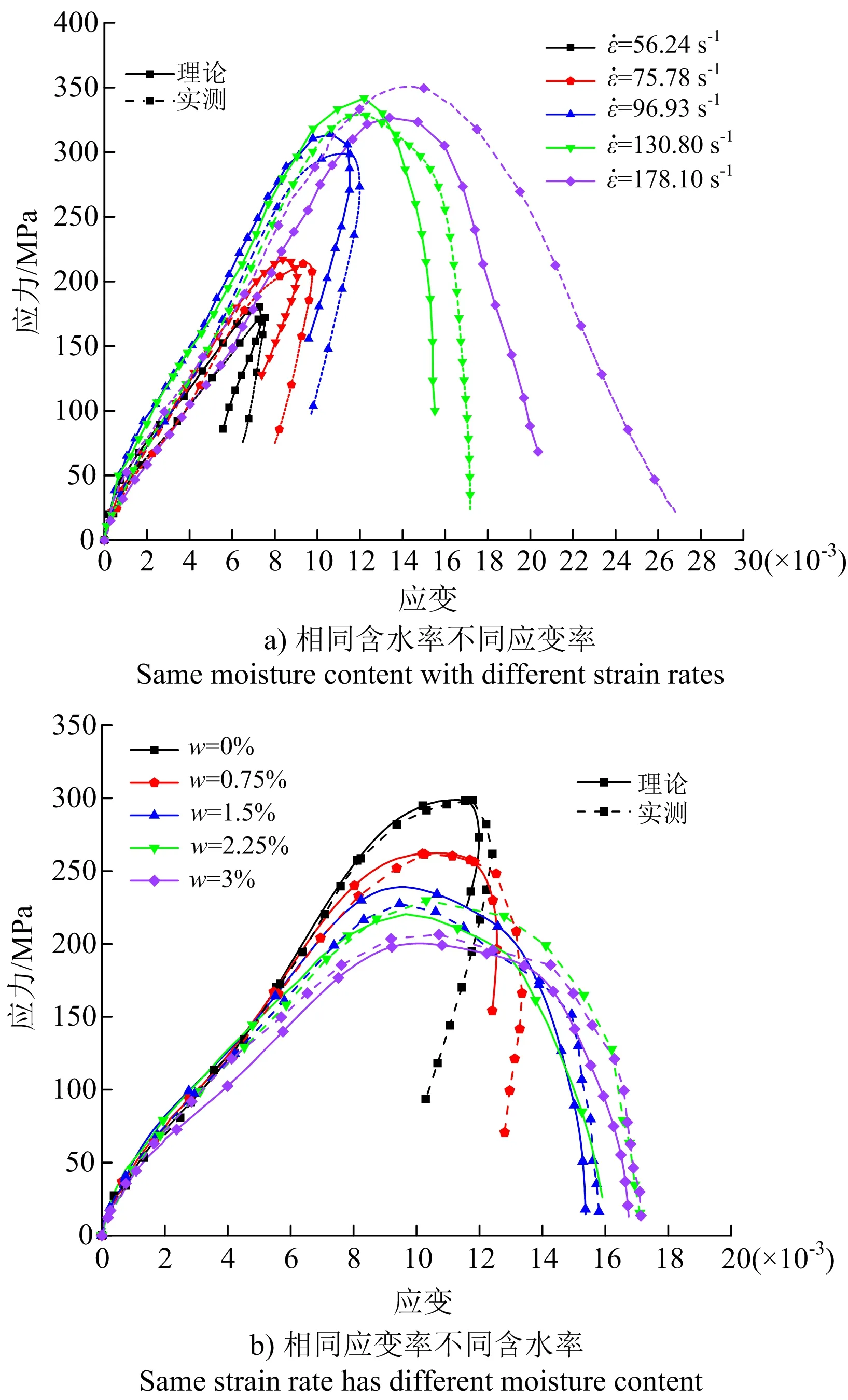
图9 含水红砂岩动态本构模型检验

从图9可看出，利用本构模型所推导出的理论应力-应变曲线与实测应力应变曲线在试样临界破坏前，即峰前阶段拟合度较高；试样破坏后，理论与实验的结果差异较大。这是由于复合损伤变量未达到1，即红砂岩未达到临界破坏时，红砂岩的强度主要由外部荷载对岩石施加的力使得红砂岩产生轴向应变导致；在试样破坏后的阶段，红砂岩的残余应力主要是由破碎的岩块提供，由于岩石破坏的不均匀与不确定性，导致峰后阶段应力下降时理论与实测曲线拟合度一般。从上图可知，该本构模型并不能与含水红砂岩在动态压缩下应力-应变曲线的各个阶段完全对应，还需要进一步的改善。

5 结论

1)推导得到了红砂岩在含水率与应变率耦合作用下的复合损伤变量与动态损伤本构方程。

2)含水损伤D1在一定范围内随含水率的增加而逐渐扩大，随着试样逐渐饱和，含水损伤趋于稳定。复合损伤Dω与荷载损伤D2在应变率的作用下变化趋势近似，分为3个阶段，即初始阶段、低速发展阶段与快速发展阶段。3个阶段代表了岩石受动荷载作用时的破坏过程，可与含水红砂岩动态压缩破坏过程应力-应变曲线的各个阶段相对应。

3)推导建立的含水红砂岩动态损伤本构模型，可以较好地描述含水红砂岩动态压缩应力-应变曲线的各个阶段，验证了该模型的准确性与合理性。