基于高斯混合模型的发动机稳态数据特征值提取方法

2022-11-28朱赤洲

航空发动机 2022年5期

哈圣，徐昊，唐震，朱赤洲

（中国航发沈阳发动机研究所，沈阳 110015）

0 引言

航空发动机稳态性能参数是表征发动机技术状态的重要参量，对这些参数的准确测量是发动机研制和使用过程都必须关注的重要问题之一。数据测量不可避免地受到环境因素和测试系统本身的影响，测得的数据中会存在噪声[1-2]。随着测量设备采样率的提升，稳态数据样本点数量往往数以千计。有时试验需要的稳态采样时间较长，其样本数量成倍增加，噪声数据的样本点数量也随之增加。数据的充分利用与数据量增加带来筛选难度增大的矛盾问题较为尖锐。由数据噪声引入的异常值无论其数据显著性强弱与否，在大量数据的累积效应下将会影响性能评估结果的准确性。因此，数据中的噪声直接影响发动机稳态性能的考核结果，不利于发动机研制，并且如何合理利用发动机稳态数据进行融合以反映发动机实际稳态工作特性成为难点。

针对数据噪声的剔除与融合方法在数据处理领域开展了大量应用性研究，如模糊指数滑动平均滤波法对数据进行滤波[3]以及基于模糊一致性矩阵的多源多模型加权决策融合诊断方法[4]。叶川等[1]对工程中常用的莱茵达准则、狄克逊准则等异常值剔除方法进行较为详细介绍，表明其评判标准在于置信区间的选择；陈震宇等[5]基于分布图法对航空发动机稳态数据异常值进行剔除，并采用分批估计方法进行数据融合，提升了稳态数据计算结果的可靠性。由于此类方法大多建立在数据源为单一正态分布特性基础上，其理论依据主要是试验参数采用等精度传感器测量，且测量形式符合中心极限定理使用情况[6-7]，通过对置信区间的选定来剔除异常值，适用于小样本空间，若置信区间划分不当容易删除有用的原始数据，从而影响数据信息整合。随着机器学习的兴起，许多专家与学者采用智能分类算法进行异常值剔除，常见的有K-means聚类算法[8-10]、LOF离异值检测算法等[11]。章永来等[12]介绍了关于K-means算法自20世纪60年代以来经Bradley与Berkhin等在原算法的基础上不断改进与优化后，提升算法本身收敛速度并扩展到了分布式聚类领域，使其成为应用较广、较为高效的聚类方法，广泛应用于对数据异常值的剔除。虽然该聚类方法属于无监督学习方法，但划分方式大多依靠闵可夫斯基距离，且属于硬聚类，发动机稳态试验数据测量值的正态性无法很好地以概率方式表征，使得该方法对发动机稳态数据异常值剔除的适用性不强。

大数据技术在航空发动机研发领域也愈发体现其价值性[13]。为此，本文采用期望极大（Exceptation Maximization algorithm，EM）算法[14-15]来求解高斯混合模型（Gaussian mivtnre model,GMM）。利用混合模型自身良好的回归特性表征数据结构，通过EM算法在逐步迭代过程中能够近似实现对观测数据的极大似然估计特性[16-17]，提出了发动机稳态试验数据特征值的提取方法。

1 高斯混合模型及模型求解方法

1.1 模型介绍

高斯混合模型是指模型本身概率分布由多个高斯分布概率密度函数叠加而成的一种混合模型，其概率分布形式为

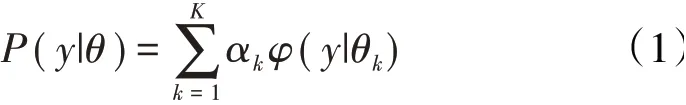
式中：K为分模型总数；y为样本点；αk为第k个分模型系数为高斯分布密度函数，为均值为方差参数，φ(y|θk)=称为第k个分模型。

1.2 高斯混合模型参数估计的EM算法

EM算法是一种迭代算法，常用于含有隐参数变量的概率模型极大似然估计，或极大后验概率估计。EM算法在每次迭代过程中包含：E步，求解模型期望值；M步，求解模型极大似然估计值[16]。EM算法在工程上是一种求解高斯混合模型的有效方法。具体求解过程如下：

（1）选取模型参数的初始值进行迭代；

（2）E步：依据当前模型参数，计算分模型k对观测数据yj的响应度

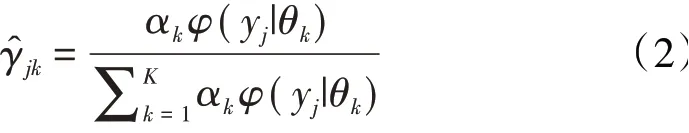
（3）M步：计算新一轮迭代的模型参数

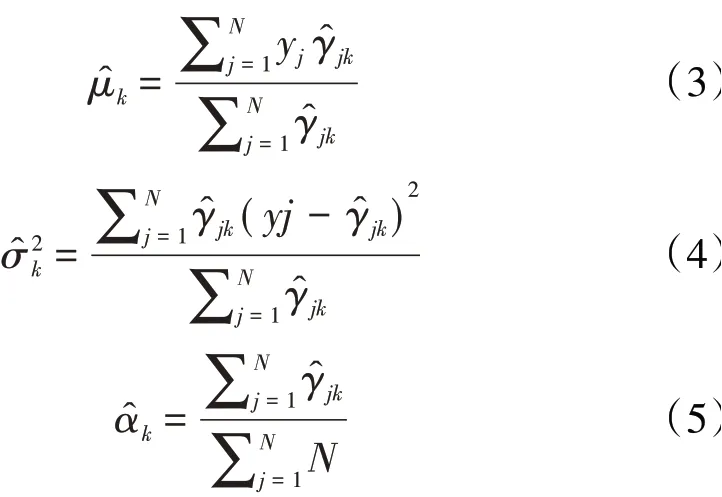
（4）重复（2）、（3）直到收敛，收敛后可认为M步最终计算各分模型参数以及近似于实际分模型参数与αk。

2 聚类数的确定方法

由第1章可知，为了充分利用混合模型良好的回归特性，需要确定高斯混合模型分模型数目，即确定数据聚类数。

本文采用赤池信息准则（Akaike Information Criterion，AIC）准则与贝叶斯信息准则（Bayesian Information Criterion,）准则的评估准则来确定数据样本的聚类数。用于评估真实模型与估计模型之间的K-L散度（Kullback-Leibler Divergence，KLD）中无偏估计项与GMM中参数数量渐近相等[18]，由此可分别利用AIC准则在小样本与BIC准则在大样本空间的模型定阶优势作为GMM聚类数的确定方法。

2.1 赤池信息准则（AIC）

AIC信息准则[19-20]又称赤池信息准则，是日本统计学家赤池弘次（H.Akaike）在解决时间序列模型定阶问题时，从随机建模观点出发针对信息论的研究提出来的基本信息量定阶准则。AIC准则在统计分析特别是在统计模型中应用广泛，其计算结果越小，说明模型接近程度越高

式中：K为模型参数数量；L为模型极大似然函数值。

2.2 贝叶斯信息准则（BIC）

与AIC准则相同，BIC准则在模型复杂性与模型对数据集的描述能力二者之间寻求最佳平衡。当数据的样本空间较大时，AIC准则由于似然函数值过大，会削弱模型参数的影响；为解决大样本空间下AIC准则的不足问题，Schwarz[21]基于贝叶斯理论提出了BIC准则，定义为

式中：N为样本数据数。

与AIC信息准则相比，BIC信息准则左边第1项用KlnN代替了2K，在大样本空间中lnN远大于2，因此在大样本数据中使用极小化BIC定出的模型阶数估计值要比AIC的低，弥补了AIC准则在大样本空间的不足，效果也更明显。

3 稳态数据正态性检验

3.1 数据正态性检验方法

航空发动机稳态数据分布特性受测量方法以及测量形式影响，数据分布特性往往服从正态分布特性。为了检验数据是否符合正态分布特性，本文稳态数据的正态性检验将分别采用主观判断法、卡方拟合优度检验（Chi-Square Goodness-of-Fit Test）和（Jarque-Bera，J-B）检验[22]相结合的方法。其中，主观判断法采用数据频数直方图以及Q-Q图（Quantile-Quantile chart）正态性检验法。Q-Q图正态性检验法是将样本得分位数与按照正态分布计算得到的分位数作为坐标轴，如果样本服从正态分布，则样本应呈1条围绕第一象限对角线的直线型散点。考虑到稳态数据的分布特性整体与局部差异性，需要对稳态数据整体性验证后再进行局部数据检验。由于Jarque-Bera检验基于偏度和峰度进行正态性检验，检验结果受异常值影响过大，因此对于局部数据正态性检验仅采用卡方拟合优度检验法。

3.2 正态性检验示例

为了充分体现数据采集系统不同来源数据特性，分别对电压信号输出的单精度压力传感器、数字量数据输出设备温度采集模块DTS3250和压力采集模块DSA3217以及频率量输出信号的采集数据进行数据特性检验，选择稳态数据参数Pjl3、T6、Ps16，Wf作为此次检验参数，其中，Pjl3为某加力区供油压力、T6为低压涡轮后温度、Ps16为外涵出口静压、Wf为频率输出的流量计测得流经发动机燃油流量，为直接测量参数。为了缩小数量相对关系以及消除量纲的影响[23]，对稳态数据进行标准分数归一化方法（z-score normalization，ZSN），转化函数为

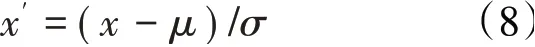
式中：x'为转换后数据；x、μ、σ分别为转换前原始数据、样本均值、标准差。

卡方拟合优度检验以及J-B检验均在5%显著水平下进行正态性检验，检验结果为0表示数据符合正态分布特性，检验结果为1表示数据不符合正态分布特性。Pjl3、T6、Ps16、Wf的稳态数据整体结果见表1，各参数的频数直方图、Q-Q图以及局部数据每组卡方拟合优度检验结果分别如图1～4所示。

从表1和图1～4中可见，发动机稳态数据大体符合正态分布特性，虽然局部检验结果存在不符合情况，但所占比例较小，其检验结果受划分数量影响，因此可认为发动机稳态数据分布特性符合正态分布。

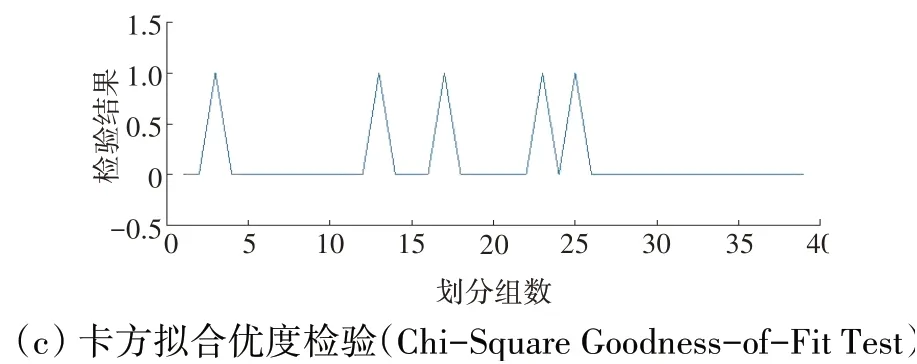
图1 Pjl3检验结果

表1 稳态数据整体性正态检验结果

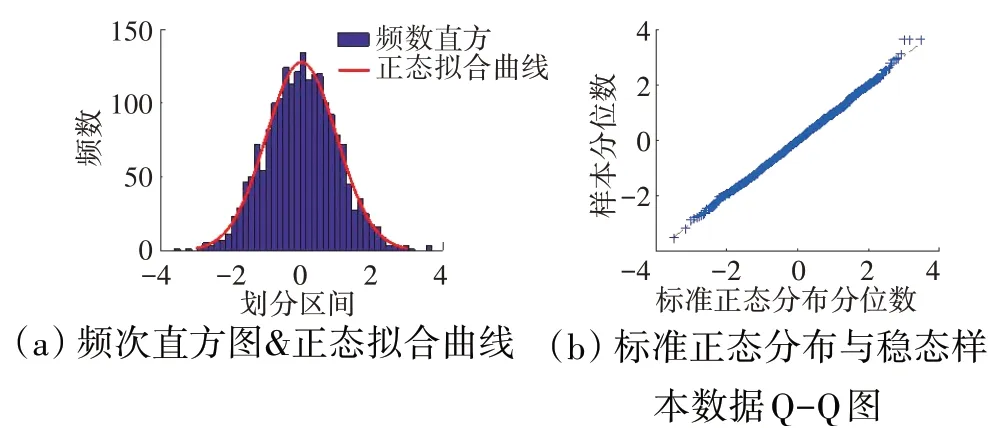
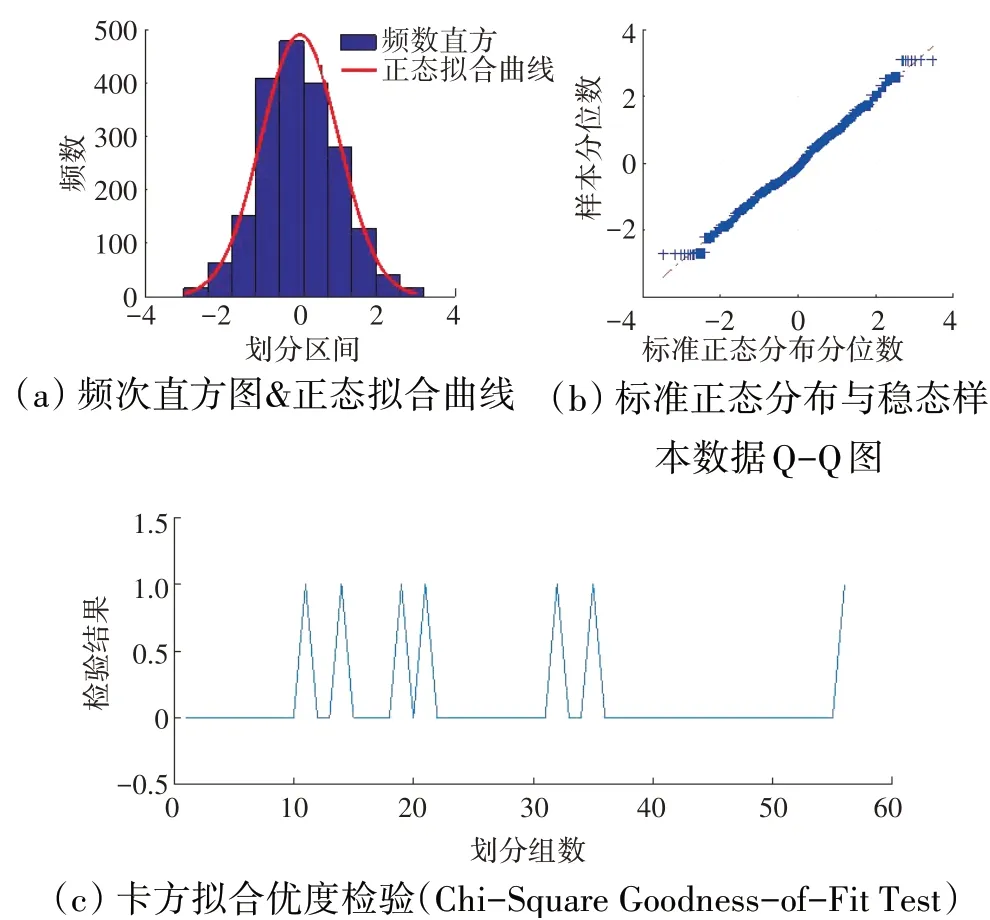
图2 T6检验结果

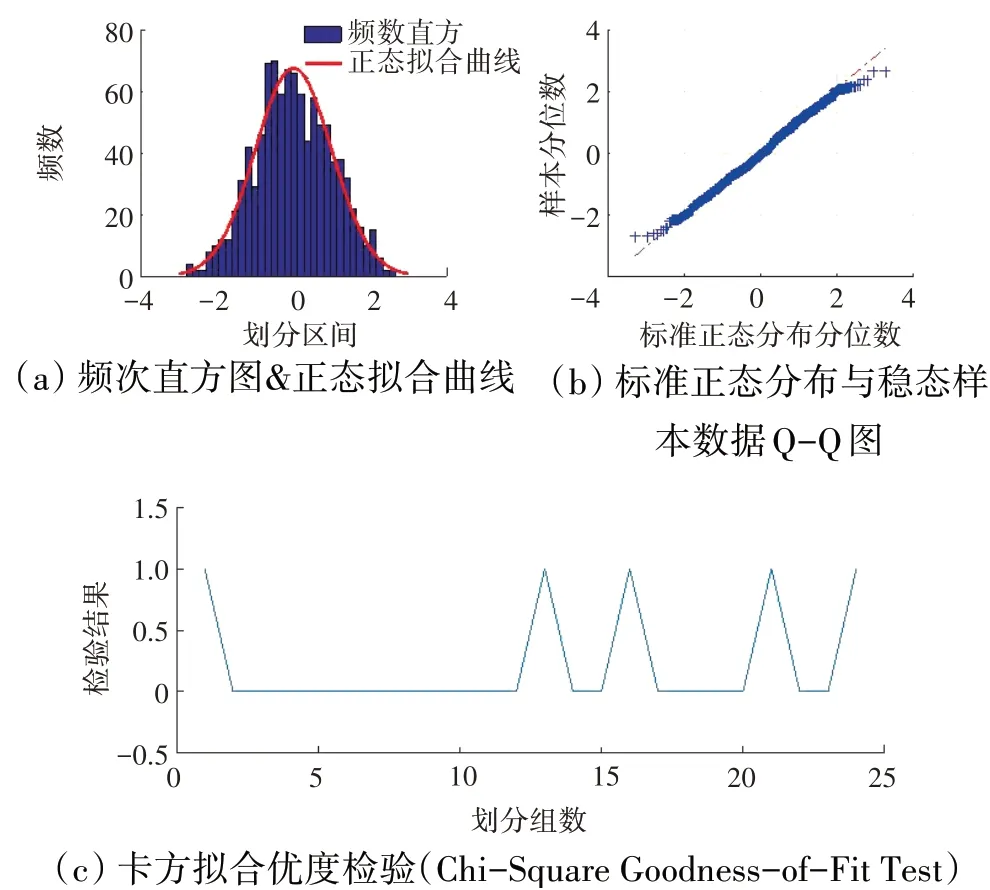
图3 Ps16检验结果

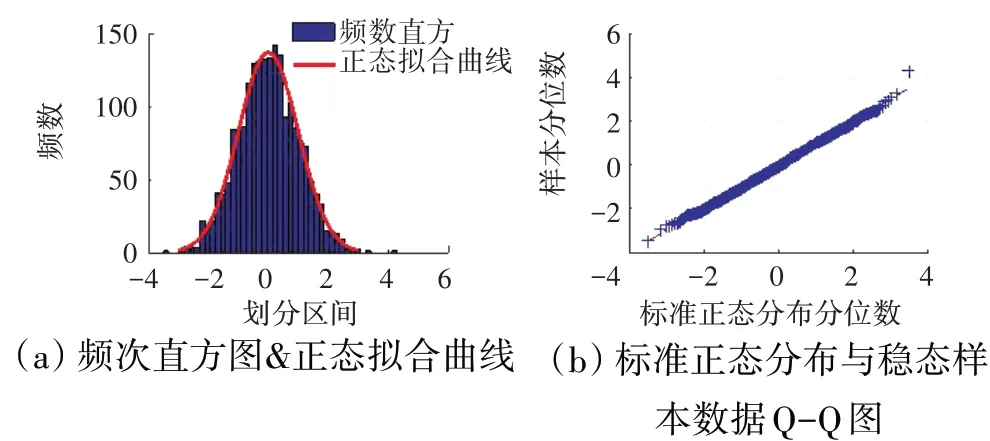
图4 Wf检验结果

4 稳态数据特征值计算方法

理论上在航空发动机稳定工作状态，其转子转速、涡轮前后的燃气温度、耗油量等参数不随时间发生变化[24]，但实际工作状态受控制规律、工作环境等多方面因素影响，其状态值会在一定范围内波动，有时会使数据本身不再满足单一正态分布特性。从时间域上看，可将这种波动视为若干个稳定工作点间的数值切换，即测量数值为若干正态分布数据值与噪声的混合叠加。

根据在试验过程中噪声数据样本点在全样本空间中的统计特性，可假设在整段稳态测量中出现非高斯噪声为小概率事件，其高斯混合模型所占权重则远小于各稳定工作点的分模型权重，那么稳态数据的特征值可写成

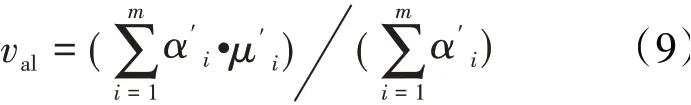
整个计算过程包括对选取稳态数据片段在高斯混合模型下最优划分形式的求解以及对筛选数据的融合计算过程，计算过程如图5所示。

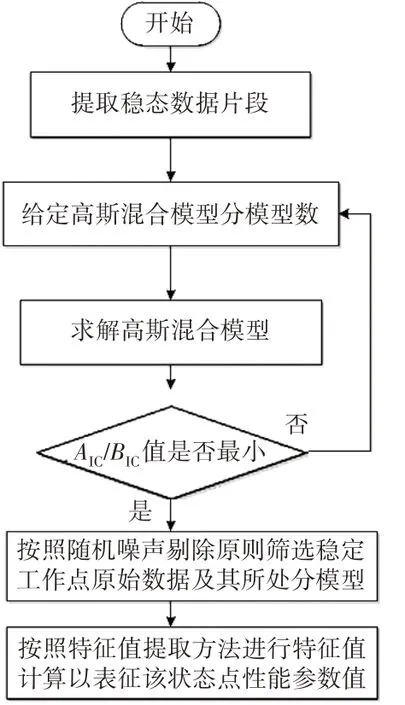
图5 稳态数据特征值计算流程

5 数据验证与结果分析

5.1 仿真计算与结果分析

为了检验高斯混合模型聚类效果以及稳态数据特征值计算结果的准确性，添加300个N（1000，4），400个N（980，3）以及300个N（1030，2）共计1000个数据点的样本作为发动机稳态数据原始样本，在原始样本中分别添加正弦与脉冲噪声，添加后的数据形式如图6所示。

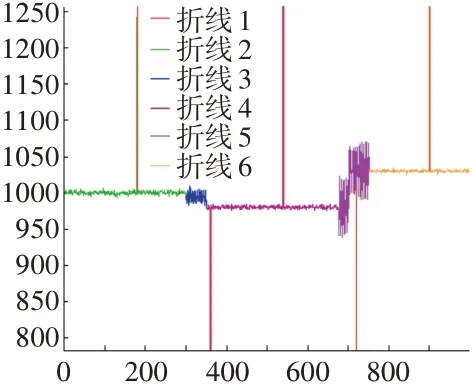
图6 数据分布形式

图中，折线1为在原始数据上添加的脉冲信号，折线3、5为在原始数据上添加的10sin（300t）+15以及40sin（300t）噪声数据。

通过计算不同聚类数的高斯混合模型的AIC与BIC准则来确定分模型的数量。聚类数K与AIC、BIC计算值的关系见表2。

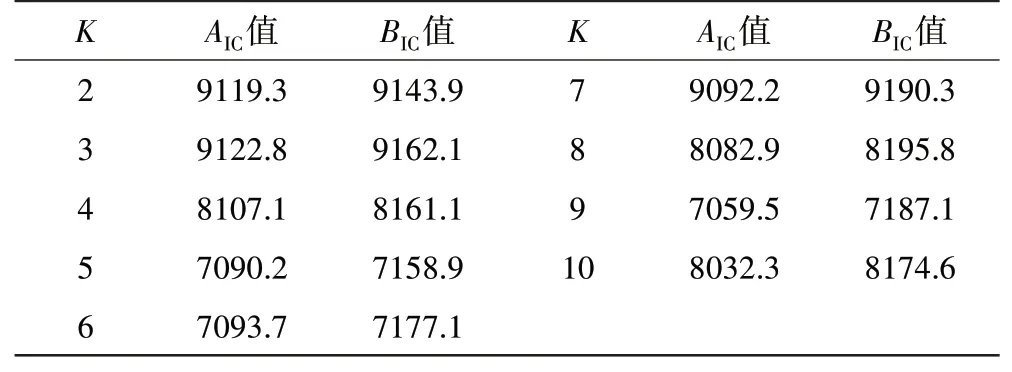
表2 不同聚类数AIC与BIC计算结果

根据大样本数据BIC最小原则，确定聚类数为5，得到聚类效果散点，如图7所示。

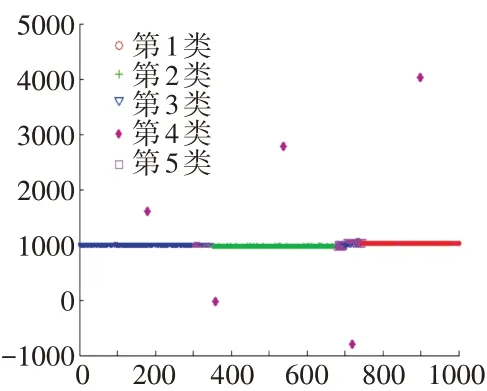
图7 数据聚类效果散点（K=5）

各分模型计算结果及分类情况见表3。

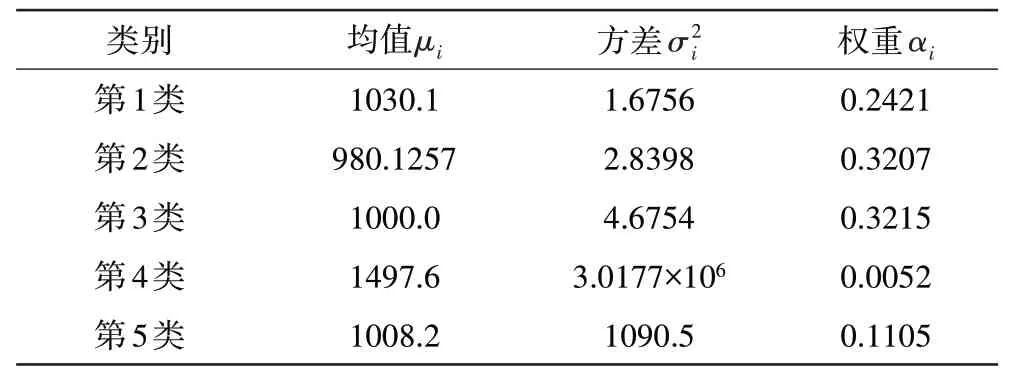
表3 数据分类结果（K=5）

根据稳态特性数据分布相似的基本原则，选取方差量级相同的高斯分布类数据作为原始样本，按照表3中稳态数据特征值计算方法，选取第1～3类均值与权重参与计算，计算结果为1001.033，具体计算过程为

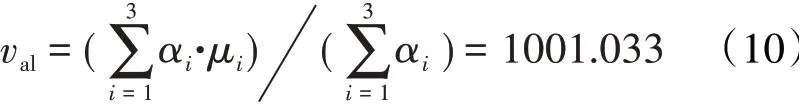
由已知原始分布数据可知原始实际值为1001.000，计算所得数据特征值相对误差为0.033%。

5.2 稳态数据验证结果与分析

为了验证高斯混合模型对真实发动机稳态数据的降噪效果以及稳态数据时间片段选取不同对计算结果的差异性进行评估，对某一参数稳态数据波动较大的数据片段进行模型验证，该原始数据在不同聚类数下AIC与BIC值计算结果见表4。

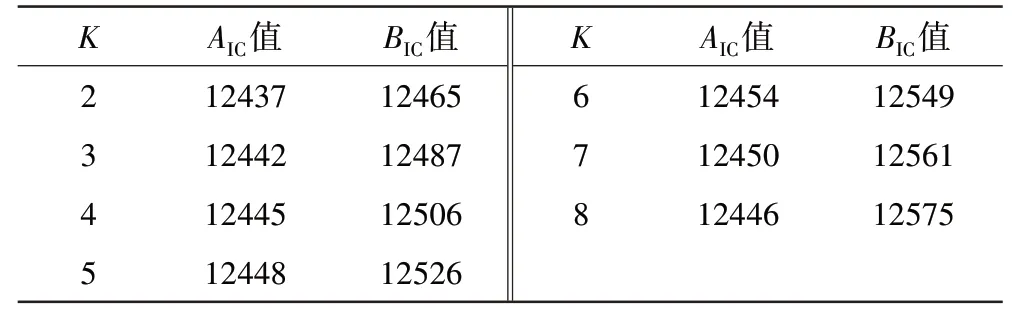
表4 原始数据聚类结果

从表中可见，当K=2，3时模型结果划分较优，原始数据划分类别为2和3的计算结果见表5，划分结果如图8所示。

表5 K=2、3的数据计算结果

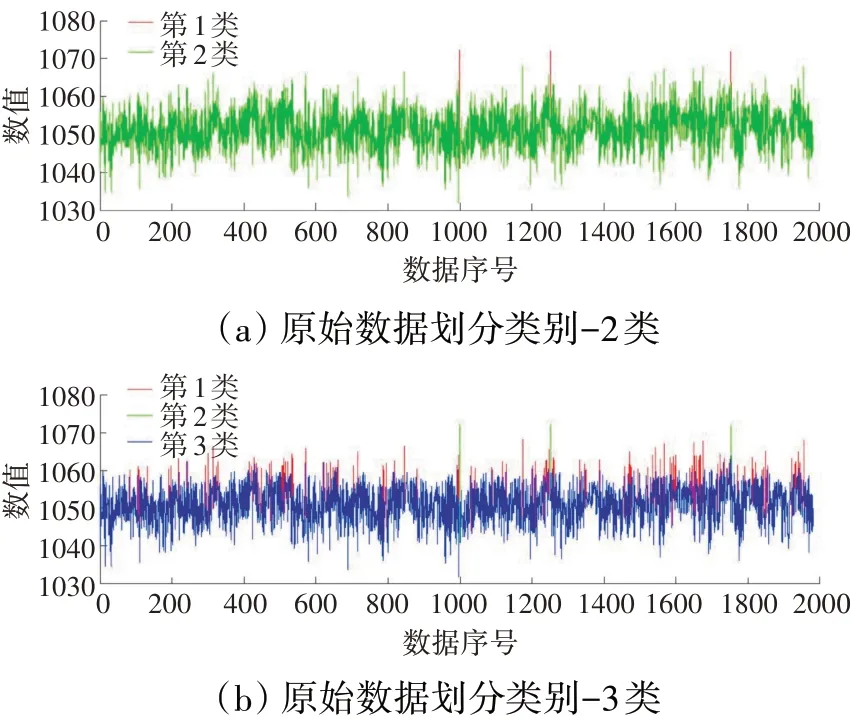
图8 原始数据划分结果

考虑稳态数据片段选择对数据稳态特征值计算结果的影响，从总的稳态数据中随机选取2组不同时间片段数据进行模型分类验证，各片段参数计算结果见表6，2组数据最优划分结果如图9所示。

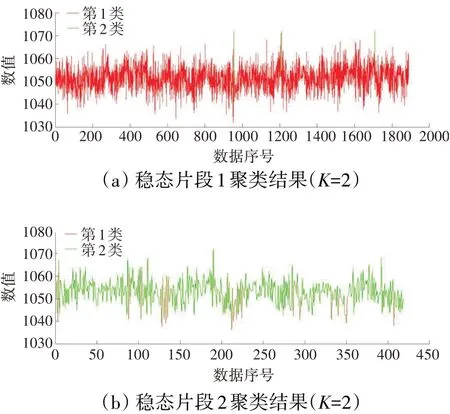
图9 不同稳态时间片段聚类效果

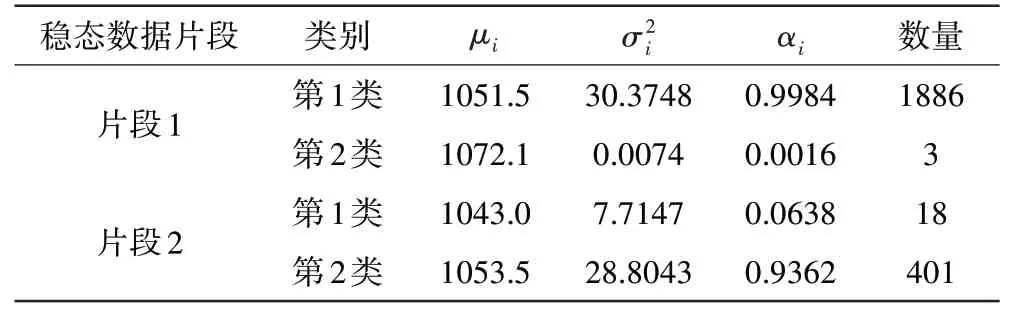
表6 2组数据片段在K=2时的计算结果

从图7中的划分结果可知，经高斯混合模型进行数据筛选后的稳态数据波动水平降低，可达到降噪效果。

从第4章中的稳态数据特征值计算方法可知总体稳态数据以及2组稳态数据片段计算结果均为K=2时权重最大类的均值，片段1与总体稳态数据特征值计算结果相差0.0095%，而片段2与总体稳态数据特征值计算结果相差0.2%，片段1、2的整体差异性不大，计算结果与发动机稳定工作状态数据性能参数不随时间变化的理论特性相符。