电阻应变计敏感栅结构参数对其测量精度的影响
2022-11-28王崇武艾延廷李成刚宋瑞如张岩松
王崇武,艾延廷,李成刚,宋瑞如,张岩松,王 志
(1.辽宁省航空推进系统先进测试技术重点实验室,沈阳 110136;2.中国航发沈阳发动机研究所,沈阳 110015)
0 引言
电阻应变计安装方便、测量灵敏度高、量程范围大、频率响应快,广泛应用于航空航天结构静力学及其疲劳试验[1]。高温应变计测试技术作为研保条件与航空发动机研制密切相关,在高温、高压、高转速的恶劣环境下,用于研究涡轮等热端部件的力学行为和使用寿命。随着新材料、新技术的应用,航空发动机和燃气轮机性能不断提高,对高温应力应变的准确测量提出了更高要求[2]。应变计组成元件尤其是敏感栅的结构参数在很大程度上影响其测试精度,为此,国内外学者做了大量研究。王彪等[3]通过建立电阻应变计的应变传递2维模型,深入分析了胶接层的结构参数对应变传递的影响;尹福严[4]通过有限元计算分析,研究了箔式应变计的应变传递机理及胶层蠕变对应变传递灵敏度的影响;Ajovalasit等[5-6]在不考虑胶接层影响的前提下,得到了应变计测量值与真实值之间的解析关系式,修正了金属粘贴式电阻应变计的应变灵敏系数;Fuyu等[7]通过有限元仿真研究了高精度传感器输出非线性误差的影响因素并计算了误差值,推导了由应变梯度引起的非线性误差的计算公式;Zike等[8]建立了金属粘贴式电阻应变计的2维和3维应变传递模型,对不同弹性模量的基底材料对应变测量的影响进行了研究;庄重等[9]对应变测试中横向效应引起的误差进行了研究,探讨在应变测量中的横向效应修正问题;王文瑞等[10]设计了自由框架丝栅式应变计,并对高温应变测量精度的影响因素进行了研究,获得了丝式应变计结构参数对测量精度的影响规律;胡玉梅等[11]建立了含应变计的悬臂梁模型,分析了丝式应变计敏感栅不同直径、栅丝长度、栅丝间距对应变传递的影响,表明栅长、栅丝间距在基体应变传递中具有中间最优值,栅丝直径越小应变传递误差越小;许艺青等[12]利用有限元分析,研究了箔式应变计不同的敏感栅材料、厚度、栅丝长宽比、栅丝间距以及粘接层几何参数和力学性能等对应变传递的影响,并利用正交试验法对敏感栅结构进行了优化设计[13]。
综上所述可知,目前国内外对电阻应变计的研究主要集中于箔式应变计各元件结构参数以及丝式应变计粘贴工艺、胶层材料对其测量性能的影响方面,而针对丝式应变计敏感栅结构参数对测量精度的影响问题研究较少,且研究的参数相对单一,只能定性地确定栅丝长度、栅丝间距等参数与测量误差之间的关系,没有揭示测量误差与敏感栅结构参数的函数关系。
本文为揭示电阻应变计敏感栅结构参数对测量精度的影响规律,建立了3维简化模型,利用ANSYS软件对常温下丝式应变计不同敏感栅结构进行数值模拟。
1 应变计有限元建模及理论验证
1.1 应变计3维模型建立
电阻应变计主要由敏感栅、粘接剂、基底、覆盖层、引出线组成。敏感栅是应变计的主要组成部分,用于将被测表面的应变转换成电阻的相对变化,敏感栅结构如图1所示。

图1 敏感栅结构
为详细研究不同的敏感栅结构参数对应变计测量精度的影响,本文建立了“简支梁-过渡层-基底-敏感栅丝”结构3维有限元模型。应变计组成部分截面如图2所示,模型各部分的几何尺寸及力学性能参数见表1。

图2 应变计组成部分截面
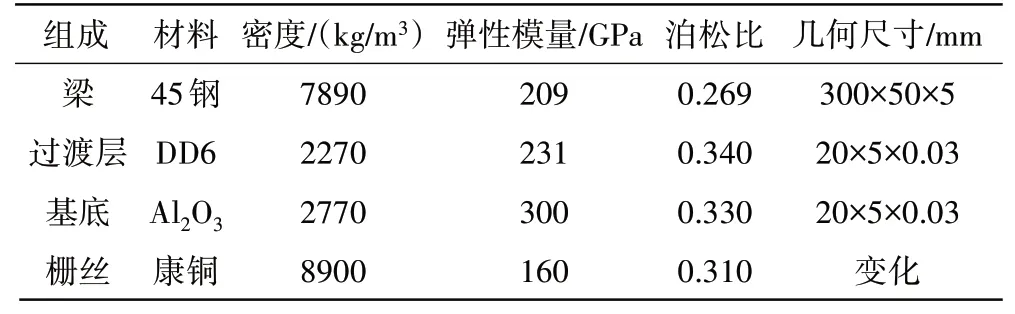
表1 模型各部分的几何尺寸和力学性能参数
在有限元模型中,应变计粘贴在简支梁中部等应变区,在距离梁两端各50 mm处向下施加500 N的载荷。栅丝网格采用sweep扫掠网格划分,其余结构采用六面体网格划分,并在过渡层与梁之间接触处及栅丝附近进行网格加密。各部分之间用bonded绑定接触粘接。有限元模型网格划分如图3所示。
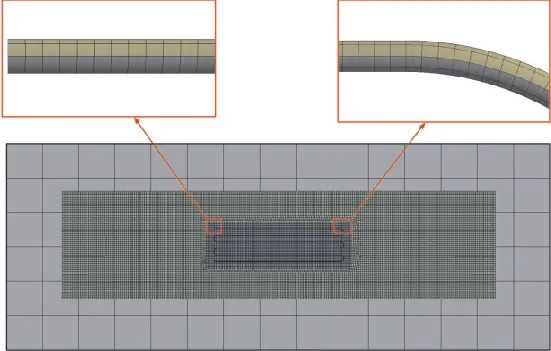
图3 有限元模型网格划分
1.2 理论验证
根据材料力学相关知识,简支梁中部为纯弯曲,其弯矩为
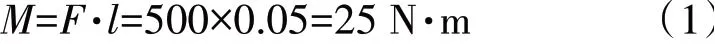
式中:F为施加的外载荷,N;l为加载点到梁端点的距离,m。
贴片处应力为
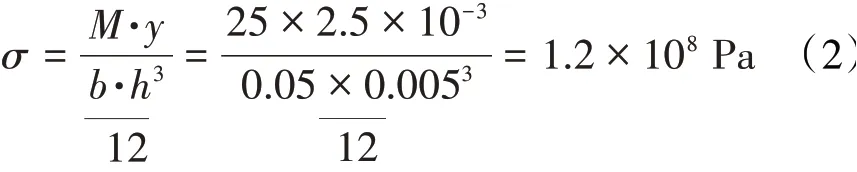
式中:y为梁截面形心至梁上表面的距离,m;b为简支梁宽度,m;h为简支梁厚度,m。
贴片处应变值为
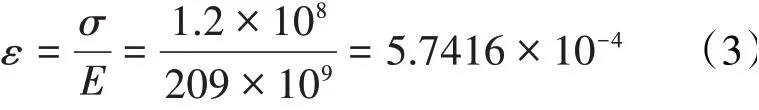
式中:E为简支梁弹性模量,Pa。
对模型进行求解,简支梁贴片位置沿x方向的应变分布如图4所示。图中,L为栅丝长度。

图4 简支梁贴片处应变分布
从图中可见,简支梁在贴片位置的应变仿真值为5.6809×10-4,理论计算值为5.7416×10-4,二者基本一致,相对误差仅为1.06%,说明贴片后该位置的应变几乎没有受到影响,可对模型做进一步分析。
在建模过程中,将敏感栅丝横截面切割成4等分,然后通过“form new part”合成1个栅丝整体(图3),获得了穿过所有栅丝横截面圆心的1个路径,通过查看整个路径上的节点应变值可以有效地提取栅丝的应变。栅丝路径的应变分布如图5所示。
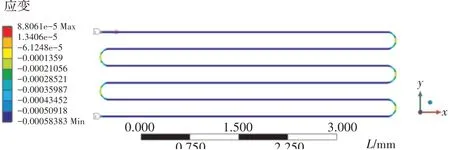
图5 栅丝路径应变分布
提取穿过栅丝横截面圆心路径上所有节点沿x方向的应变值,取平均值作为栅丝的输出应变,并与梁贴片处的应变进行比较,得出相对误差δ作为应变计的应变传递误差

式中:εs为栅丝的输出应变;εl为贴片处梁的应变。
栅丝全路径应变值变化如图6所示。
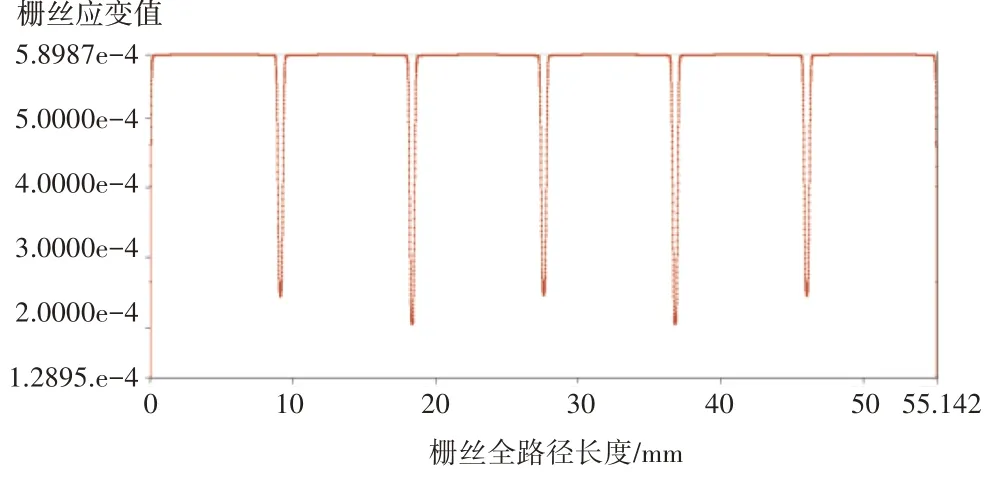
图6 栅丝全路径应变值变化
随机改变栅丝结构参数(栅丝长度L、栅丝间距S)进行5组仿真计算,得到敏感栅输出应变值与贴片处梁应变的相对误差σ,不同栅丝结构参数仿真计算结果见表2。
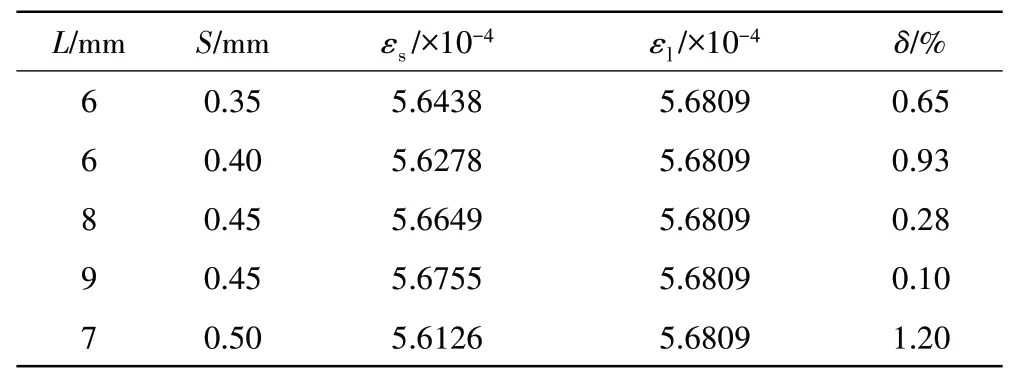
表2 不同栅丝结构参数仿真计算结果
从表中可见,敏感栅丝的输出应变与梁贴片处应变误差较小,约为1%,表明在该有限元模型中应变计可以比较准确地反映被测基体的应变,说明该模型有效,可用于下一步研究。
2 敏感栅结构参数对测量精度的影响
2.1 栅丝直径对测量精度的影响
栅丝直径d越小,测量越准确[11]。在有限元模型中,保持栅丝长度、栅丝间距等参数一致,改变栅丝直径进行仿真计算。栅丝直径在0.02~0.04 mm内以5 μm为间距变化,应变测量误差随栅丝直径的变化曲线如图7所示。
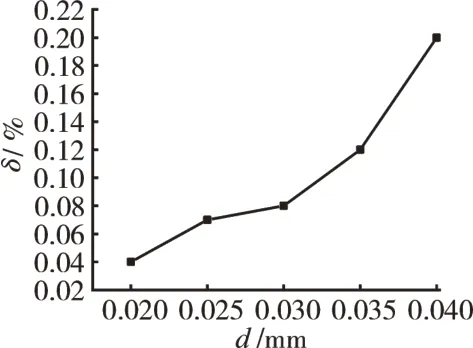
图7 应变测量误差随栅丝直径的变化曲线
从图中可见,随着栅丝直径增大,测量误差也变大。这与已知规律相符,即敏感栅越细,越能均匀且准确地反映被测构件表面的变形,测量误差也就越小。但在实际应用中,栅丝直径过小会导致栅丝强度降低,容易发生断裂;而栅丝直径过大又会使得应变感应灵敏度降低。所以在选用应变计时应根据实际情况综合考虑。
2.2 栅丝长度对测量精度的影响
在测量中敏感栅栅长与被测基体主应变方向一致,因此栅丝的长度尺寸会对误差产生较大影响,决定着应变计的测量精度[14]。
在有限元模型中,保持其他结构参数不变,在5~11 mm内以1 mm为间距研究栅丝长度L变化时应变计的输出应变,并设置4组不同的栅丝间距S作为对照组,5组间距分别为0.30、0.35、0.40、0.45、0.50 mm。测量误差随栅丝长度的变化曲线如图8所示。
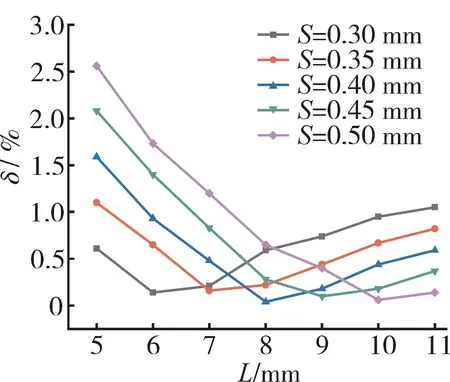
图8 测量误差随栅丝长度的变化曲线
从图中可见,随着栅丝长度的增加,误差先减小后增大,栅丝长度具有中间最优值,且栅丝长度最优值随栅丝间距的增大而增大。
2.3 栅丝间距对测量精度的影响
栅丝间距的改变会影响粘接层的应力应变分布以及应变片的横向效应[15],从而改变栅丝的输出应变,进而对测量误差产生影响。
保持其他结构参数不变,在栅丝间距为0.25~0.55 mm内 以0.05 mm为间隔对应变计进行仿真计算,并设置栅长为6~10 mm共5个对照组。应变测量误差随栅丝间距的变化曲线如图9所示。
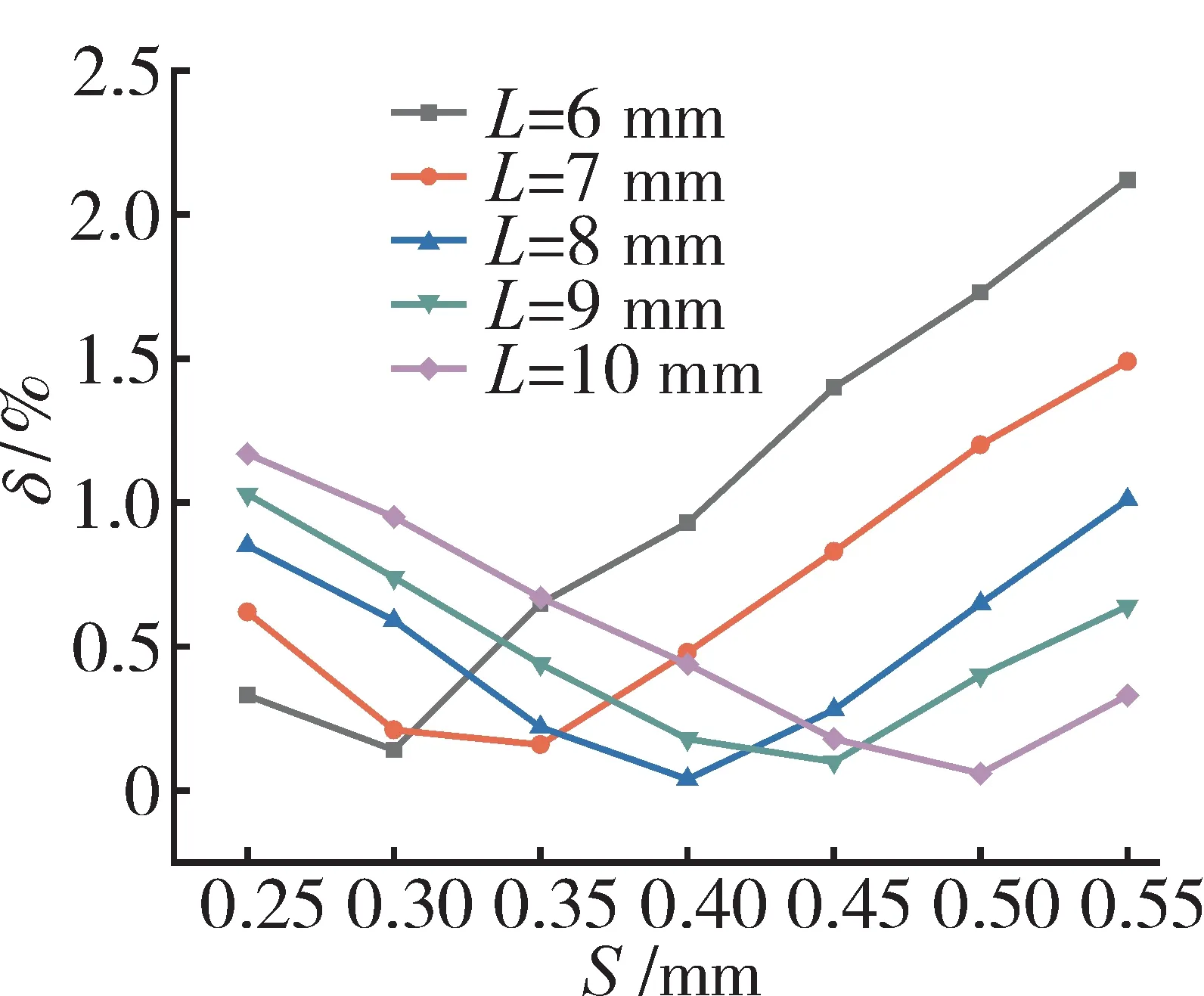
图9 应变测量误差随栅丝间距的变化曲线
从图中可见,测量误差随栅丝间距的增大先减小后增大,栅丝间距具有中间最优值,且间距最优值随着栅丝长度的增加而增大。
2.4 栅丝弯数对测量精度的影响
栅丝的弯数N影响长宽比,决定了栅丝的数目和排列方式。保持其他结构参数一致,利用仿真计算获得N=1、3、5、7、9时栅丝的输出应变,并随机设置4组对照组,5组参数组合的栅长+间距分别为6 mm+0.3 mm、7 mm+0.35 mm、8 mm+0.4 mm、10 mm+0.5 mm、10 mm+0.45 mm,其应变测量误差随栅丝弯数的变化曲线如图10所示。
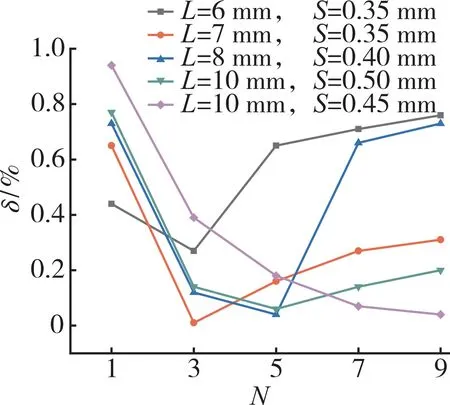
图10 应变测量误差随栅丝弯数的变化曲线
从图中可见,随着弯数的增加,测量误差先减小后增大,弯数也有中间最优值,且不同的参数组合具有不同的最优值。在实际应用中丝式应变计多设计为5弯(图1),但5弯并不一定是最佳弯数,可根据实际要求和制作条件灵活设计和选用。
2.5 栅丝长宽比对测量精度的影响
栅丝的长度和宽度决定了栅丝的几何尺寸(图1),为此设计了不同的参数组合进行仿真计算,具体结构参数取值见表3。其中,栅丝长度L、栅丝间距S分别为5组,栅丝弯数N为4组,进行5×5×4共100组仿真计算。
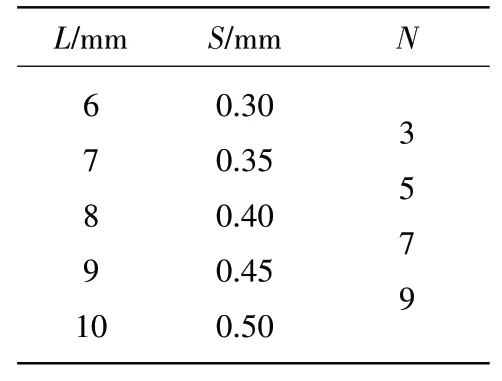
表3 栅丝不同参数取值
应变测量误差随不同栅丝长宽比变化的散点如图11所示。从图中可见,测量误差随栅丝长宽比的增大先减小后增大,长宽比亦有中间最优值,且最佳长宽比随着栅丝弯数的增加而减小。
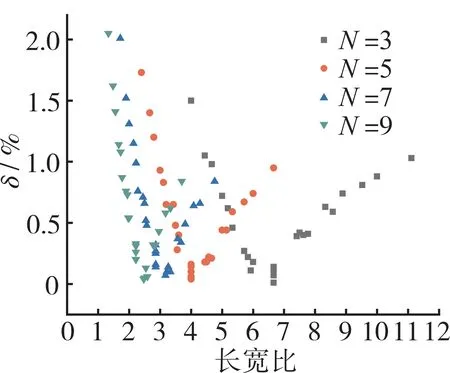
图11 应变测量误差随不同栅丝长宽比变化的散点
2.6 栅丝横向效应长度比与测量误差的关系
理想的应变计不存在横向效应,但在实际应用中应变计都存在横向效应,在某些应变测量中,横向效应会使测量结果产生较大误差。敏感栅的弯曲部分是产生横向效应的根源。
通过上述研究可以发现,丝式电阻应变计敏感栅丝的长度、间距、弯数、长宽比皆呈现出“最优值”规律,而这4种参数都是敏感栅尺寸在不同维度的呈现,不同的参数变化实际上是横向效应产生的应变占栅丝输出应变比重的变化。为了统一这种参数变化,在结构层面,本文定义了一种无量纲参数——横向效应长度比η,即弯曲部分的长度占整个栅丝长度的百分比

从式中可见,η随L的增加而减小,随S的增大而变大,随N的增加而变大。
对表3中100组参数组合求解对应的η值,利用Origin软件绘制出测量误差随横向效应长度比η变化的100个散点分布,如图12所示。

图12 应变测量误差随横向效应长度比变化散点分布
从图中可见,二者呈现出比较明显的分段线性关系,对散点进行函数拟合,得出测量误差δ与横向效应长度比η的关系。
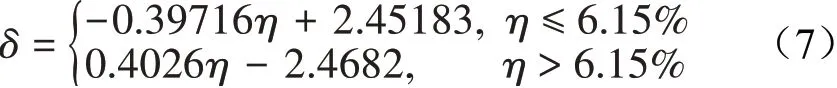
根据式(7)可知,横向效应长度比存在最优值,当η=6.15%时,δmin=0.009%。
式(7)给出了测量误差δ与栅丝长度L、栅丝间距S、弯数N之间的函数关系。为验证此关系式的正确性,另设计3组新参数组合进行仿真计算,新参数组合见表4。
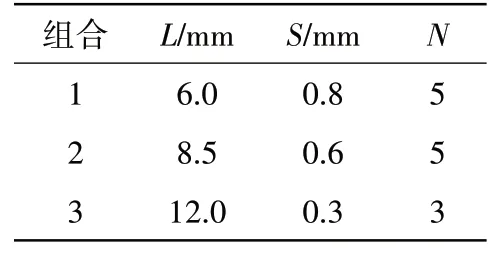
表4 新参数组合设置
关系式求解结果与仿真计算结果对比见表5。

表5 关系式求解结果与仿真计算结果比较
从表中可见,关系式求解得到的估算结果与仿真计算结果的误差不超过4%,说明此关系式具有良好的普适性,可根据此公式快速估算出给定敏感栅结构参数的应变计测量误差。
将式(7)中的η最优值6.15%代入式(6)并整理可得参数优化值(取小数点后4位)。
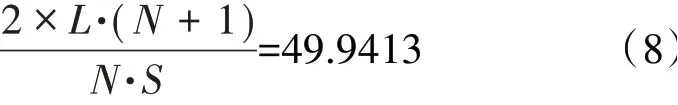
给定式(8)中任意2种结构参数,就可以计算出第3种最优参数值。为验证此优化公式的正确性,随机设计3组仿真计算,结果见表6。
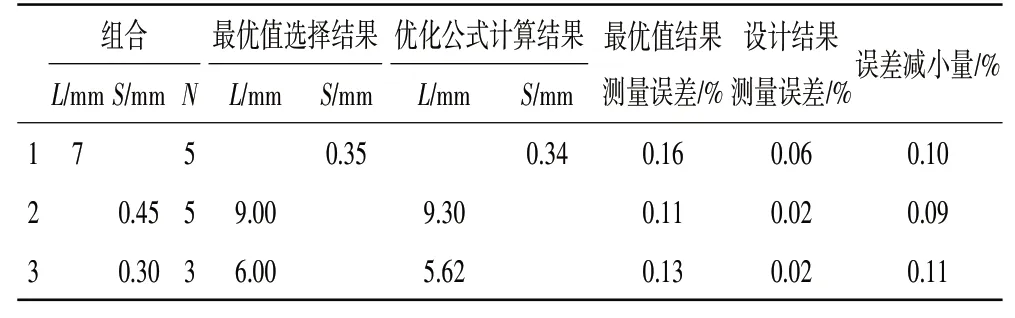
表6 优化公式仿真计算验证
从表中可见,根据式(8)计算出的参数组合得到的设计结果测量误差δ≤0.06%,与之前单独优化得出的最优值计算结果相比,测量误差均减小了0.1%左右,表明此公式对应变计的结构参数优化具有指导意义。
3 结论
(1)本文建立的应变计有限元模型的应变传递误差在1%左右,能够正确反映被测基体的应变情况。
(2)栅丝直径越小,测量误差越小;栅丝长度、间距、弯数、长宽比具有中间最优值;栅丝长度最优值随间距的增大而增大,栅丝间距最优值随栅丝长度增加而增大,长宽比最优值随弯数的增加而减小;测量误差与横向效应长度比呈分段线性函数关系,当横向效应长度比为6.15%时测量误差最小。
(3)本文提出的横向效应长度比参数可以有效地统一敏感栅的各结构参数,通过建立测量误差与横向效应长度比的函数关系,可快速估算出给定敏感栅结构参数的应变计测量误差,估算结果与仿真计算结果相对误差不超过4%,说明关系式具有良好的普适性。
(4)由测量误差与横向效应长度比的关系式推导出参数优化公式,根据优化公式设计出的应变计结构参数组合测量误差不超过0.06%,且较最优值参数组合降低了0.1%左右,可用于应变计敏感栅结构参数快速优化设计。
