基于GA优化BP算法的滑油状态监测

周 良，王华伟，许珊珊，王清薇

（1.南京航空航天大学民航学院，南京 211100；2.山东师范大学公共管理学院，济南 250300）

0 引言

滑油系统是航空发动机的重要组成部分，由于滑油的循环利用特点，其携带了大量的发动机内部信息。滑油监测技术是通过分析润滑油的性能变化和携带的磨粒，获得发动机摩擦学系统的润滑和磨损状态信息，以此评价发动机的工况和状态，并确定故障原因、类型。因此，滑油状态监测是航空发动机健康监测和故障诊断的重要手段[1-3]。通过对滑油中金属含量的预测，可监测发动机轴承、齿轮等重要部件的健康状态[4]，并及时维修或更换，以保障飞行安全和降低运营成本[5-7]。

研究人员在以滑油状态监测实现航空发动机健康监测[8-9]和故障诊断[10-11]方面进行了大量研究。修攀瑞等[12]综合运用多种滑油分析技术，有效监测了发动机传动润滑系统的磨损状态，及时发现磨损故障并确定了故障部位；马敏等[13]提出一种基于多尺度卷积神经网络、长短期记忆网络和反向传播（Back propagation,BP）网络的单通道网络模型用于滑油监测数据的特征提取，该方法以串行方式提取数据在空间维度和时间维度上的2维特征，提高了数据样本的分类精度；曹宏庆[14]以数学方法和智能算法相结合，挖掘滑油磨粒携带的信息，提高发动机滑油颗粒监测试验的科学性和准确性；陈庆贵等[15]利用径向基（Radial Basis Function，RBF）过程神经网络预测航空发动机滑油金属含量，对比单一BP网络，具有更高的预测精度，但未对RBF网络的收敛速度和迭代过程作详细对比阐述，使预测结果缺少一定说服力；曾力等[16]利用支持向量回归机（Support Vector Regression，SVR）模型对滑油金属含量进行预测，模型易向全局最优靠拢，提高了收敛速度，但试验数据较少，在一定程度上，预测结果的准确度不稳定；Lopez等[17]制订了一种传感器解决方案，可在线监测滑油的降解状况，可定性地进行滑油理化性能分析，但无法实现发动机故障预测和健康管理。

针对以往算法容易陷入局部最优，收敛速度慢，鲁棒性差以及预测精度不高等问题，本文提出一种GA-BP算法框架，将遗传算法（Genetic Algoritht,GA）用于BP网络，利用GA寻找全局最优权值和阈值，并进行BP网络的训练。

1 GA优化BP模型

1.1 模型框架

GA优化BP神经网络分为BP神经网络结构确定、GA优化和BP神经网络预测3部分。其中，BP神经网络结构确定部分根据拟合函数输入、输出参数数目确定BP神经网络结构，可以确定GA优化参数数目，进而确定GA个体的编码长度。BP神经网络用GA得到的最优个体对网络进行初始权值和阈值的赋值，网络经训练后预测样本输出。GA优化BP模型如图1所示。

图1 GA优化BP模型

根据BP网络模型，权值数为100×150+150×60+60×2=24120，阈值数为：150+60+2=212，所需优化参数的数目为：24120+212=24332。此过程是利用GA优化权值和阈值，替代BP神经网络反向传播的过程。

1.2 BP网络模型

BP网络[18-19]工作的基本原理实质上是通过对网络权值（ωij,Tij）的修正和阈值θ的修正，使误差函数E沿负梯度方向降低，并使得最终误差在允许的范围内。这里选取1个3层的神经网络，即2个隐藏层，1个输出层。BP网络模型如图2所示。

图2 BP网络模型

输入节点为Xi，隐藏层节点分别设为Yj,Zk，输出节点为Cm，连接输入节点与隐藏层节点之间的权值和阈值设为ω（1）ij，θ（1）j，隐层节点之间的权值和阈值设为ω（2）jk，θ（2）k，隐藏层和输出层之间的权值和阈值设为ω（3）km，θ（3）m。

1.3 GA模型

GA模型[20]通过模拟生物界自然选择和自然遗传机制的进化过程，采用自然选择、遗传、变异等作用机制，得到适应度最高的个体。GA算法在解决大空间、多峰值、非线性和全局优化等问题上具有显著优势[21-22]。GA模型如图3所示。

图3 GA模型

2 GA优化BP算法原理

2.1 算法流程

GA优化BP网络算法流程如图4所示。

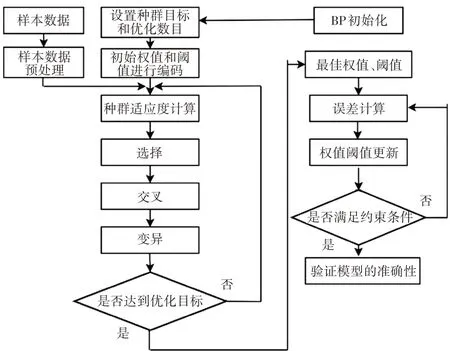
图4 GA优化BP网络算法流程

2.2 BP神经网络算法

（1）对于隐层节点Yj来说，其计算输出为

（2）对于隐层节点Zk，其计算输出为

（3）输出节点的计算输出为

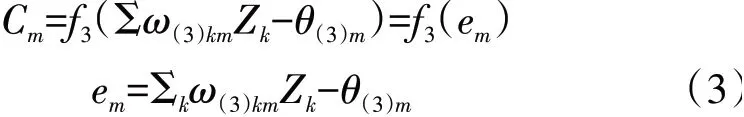
（4）若输出节点的期望输出设为Om时，则输出节点的误差为

（5）权值修正

（6）阈值修正

2.3 GA算法

（1）此算法最终目的是得到误差最小的权值和阈值，因此，目标函数为最小化问题，可写为

（2）适应度函数为

式中：Fit为适应度函数；c为常数。

（3）编码。假如参数的取值范围为[Umin，Umax]，用长度为λ的二进制的编码符号串来表示该参数，那么一共可产生2λ种不同的编码，以δ表示二进制编码的精度

（4）解码。假设个体的编码是x：bλbλ-1…b1，那么对应的解码公式为

（5）选择。设第t代种群A（t）中所能匹配的样本数为m，记为m（H，t）。设第1代中群体大小为n，则第t+1代中样本数为

式中：f（H）为平均适应度；fi为个体适应度。

（6）交叉。假设2个个体XA，XB之间进行交叉，则交叉运算后所产生的2个新个体为

式中：α为参数，若为常数，则可称为均匀算术交叉，若α为变量，则此时的交叉运算可称为非均匀算术交叉。

在交叉后模式H的生存概率为Ps，遭到破坏的概率为Pd，发生交叉的概率为Pc，故H生存的概率为

（7）变异。设串的某一位置发生改变的概率为Pm，那么，不变的概率为1-Pm，当Pm＜＜1时，模式H在变异作用下生存概率为

式中：o（H）为模式H的阶数。

2.4 Bayes决策

状态空间可设置为Ω=（ω1，ω2，…，ωm），在状态监测中，主要判断工况故障与否，先验概率用P（ω1）、P（ω2）表示，p（x|ω1）为正常状态的条件概率密度函数，p（x|ω2）为故障状态的密度函数，P（ωi|x）表示已知样本条件下ωi出现的概率。

（1）对2类状态有

（2）决策规则

（3）错误率计算

（4）由式（3）～（16）可知，P(ωi|x)＞P(ωi|x)，决策ωi，在此决策下，错误概率P(ωi|x)为

3 算例

数据来源于某型号通用航空发动机从一次换油到另一次换油完整工作阶段的滑油光谱分析数据。在滑油的监测过程中，以铁的质量为主要的监测对象。从滑油光谱数据中得到铁的质量时间序列数据共161个，如图5所示。

图5 铁的质量时间序列

以前140个数据作为网络的训练样本，最后21组数据作为网络的测试样本，用MatLab测试算法的性能，分别用GA-BP算法模型、RBF网络、SVR模型和BP网络对滑油铁的质量时间序列进行预测，并对各算法模型预测结果进行对比，以分析各算法模型的精确度和可靠性。

3.1 GA-BP模型预测结果分析

在此算法下，网络结构设为1-7-1，网络的误差精度设为1×10-5，迭代次数为100。则铁的质量的预测输出和期望输出如图6所示。GA优化BP预测结果误差如图7所示。

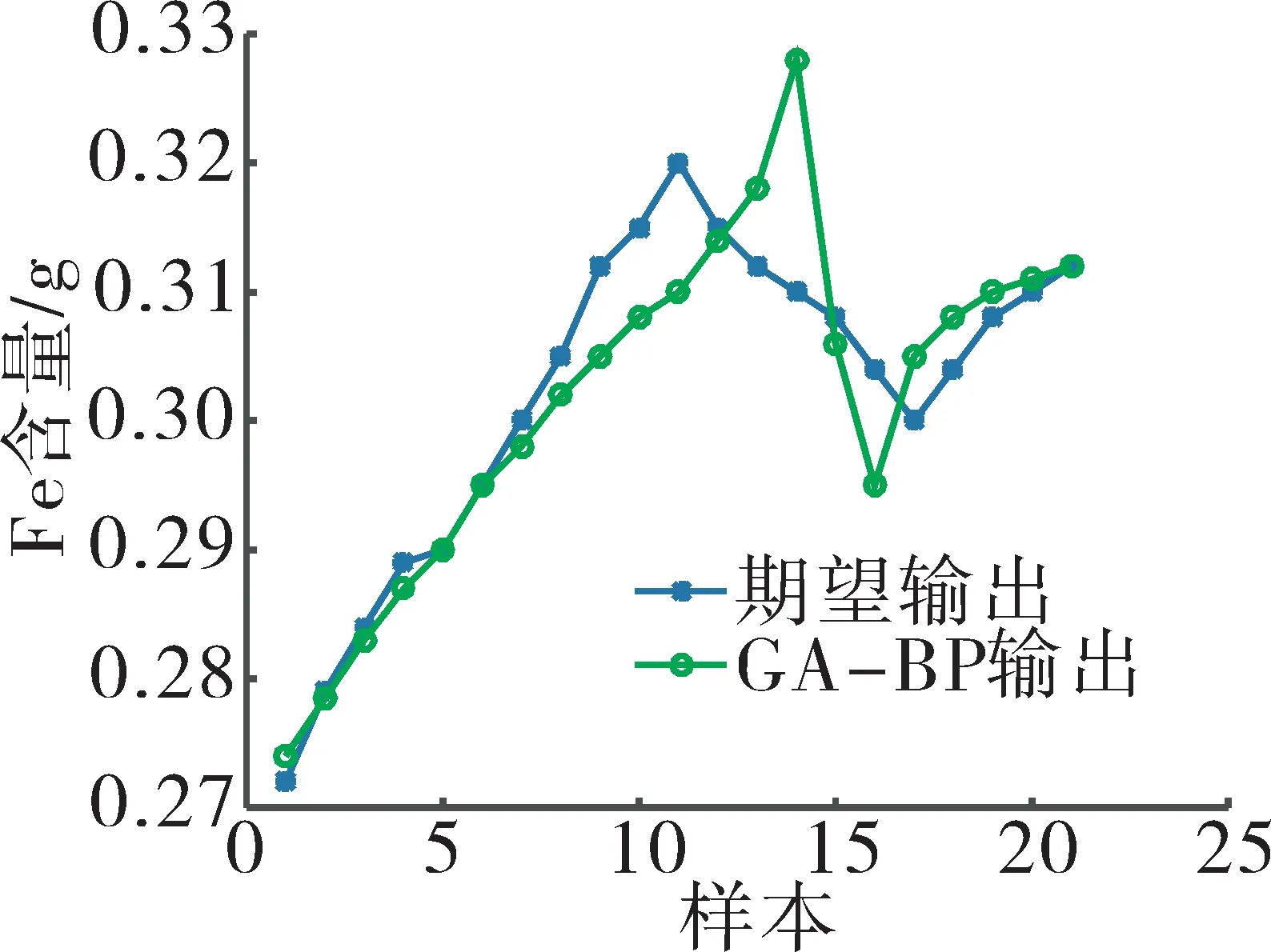
图6 GA优化BP的铁的质量预测输出和期望输出

图7 GA优化BP预测结果误差

从图6中可见，GA-BP预测数据与样本数据较为吻合，且预测数据曲线与样本数据曲线趋势一致。从图7中可见，GA-BP预测数据误差百分比最大不超过6%，预测精度较高，误差在可接受范围之内。

3.2 算法模型输出结果分析

分别利用RBF网络、SVR模型和BP网络对样本数据进行预测，并将各种算法模型的预测结果与GABP模型预测输出进行对比分析。算法模型预测结果如图8所示。各种算法模型预测结果误差对比如图9所示。

从图8中可见，与其他模型算法相比，GA-BP预测结果曲线与原数据的拟合度最高，RBF和SVR模型对预测结果都有较高的精度，BP网络在后期数据的预测中未收敛。从图9中可见，在相同训练样本的情况下，GA-BP预测误差相对处于较低水平，其预测精度优于其它模型算法。

图8 各种算法模型预测结果对比

图9 算法模型预测结果误差对比

从图8、9中可见，各算法模型前期预测数据精度较高，在样本数据出现转折时，算法模型预测数据都出现了不同程度的误差，体现出算法模型在滑油金属质量时间序列预测问题上的不稳定性。因此，为了更直观展现后期各算法模型性能，将后期各种算法模型预测误差数据进行整合，见表1。

表1 各种算法模型预测误差 %

从表中可见，GA-BP模型平均误差最小，与其他模型算法相比，其预测误差普遍偏小，在可控范围内平稳波动。

3.3 结果分析

从上述试验结果中可得，GA-BP无论是预测精度还是收敛速度都优于其它模型算法的，GA-BP网络在样本数据出现转折时，其预测误差轻微波动，但与样本数据的拟合度较高，整体误差不超过6%，平均误差为1.7%，在可控范围之内，预测精度和收敛速度较为优异，在寻优的问题上有较好的适用性。

3.4 Bayes分析

Bayes分析主要用于判断发动机工况正常和异常2种状态，以ω1、ω2表示，先验概率用P（ω1）、P（ω2）表示，且有P（ω1）+P（ω2）=1，设P（ω1）=a，则P（ω2）=1-a，以x表示某测点滑油中金属的质量分数，为了使诊断结果更具有说服力，引用悲观决策准则的思想，在滑油时间序列的测试结果中取误差最大的时刻（即第17个样本点）为本次测点，在此处滑油预测中金属质量分数x=0.322，则在正常状态下的条件概率密度函数为p（x=0.322|ω1），可设p（x=0.322|ω1）=A，同理，在异常状态下的条件概率密度函数为p（x=0.322|ω2）=B，A和B可看作关于x的一次函数。

由式（15）可得各状态下概率函数为

由式（17）计算错误率

由概率密度函数可得决策错误率图像，如图10所示。

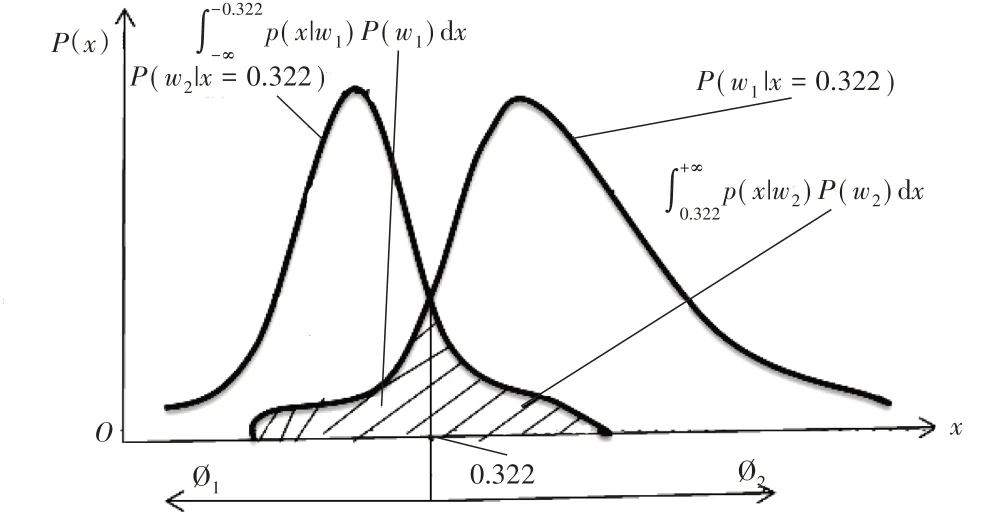
图10 决策错误率图像

由决策错误率图像分析可知，在预测结果误差最大时，决策错误率最大。为使决策错误率最小，在x＜0.322时，决策ω1即为正常状态；当x＞0.322时，决策ω2即为异常状态。即Bayes决策规则就是对每个x都使得P（e）最小，也就是错误率最小。

4 结论

（1）结合GA算法收敛速度快、鲁棒性好、泛化能力高等优点，对BP网络进行GA优化，构建了GA-BP网络模型，提高了原有BP网络的预测性能；

（2）以某型通用航空发动机滑油金属质量分数数据为例，GA-BP模型预测数据整体误差小于6%，平均误差小于1.7%，相比单一BP网络和其他算法，GA优化后的BP网络预测数据精度高，收敛速度快，训练时间短，预测结果更具可靠性；

（3）通过Bayes对诊断结果分析，当滑油金属质量分数小于0.322时，决策为正常状态，此时诊断错误率较低，提高了诊断结果的可靠度，为基于滑油状态监测对航空发动机重要部件的健康状况进行判别提供了更为全面有效的方法。