基于三维本构模型的形状记忆合金弹簧力-位移关系研究*

黄竑钢

(西南交通大学 力学与航空航天学院，四川 成都 610031)

0 引 言

形状记忆合金(Shape Memory Alloy，简称SMA)是一种新型智能材料，不仅具有独特的形状记忆效应和超弹性效应，而且有良好的阻尼特性、耐疲劳性和耐腐蚀性。 因此，它被广泛地应用于航天航空、机械电子、生物医疗等多个领域。 其中，超弹性SMA 由于其极强的滞回耗能特性，而被广泛地用作土木结构中的阻尼器，以增强结构的抗震减震效果。 因此，有必要了解SMA 弹簧的力学性能及其工作原理，对其力学行为进行详细研究，为SMA 弹簧在工程应用中的设计和使用提供依据。

SMA 的本构模型是模拟SMA 弹簧力学行为的重要部分。 目前，国内外学者们主要是基于热力学本构模型对SMA 弹簧进行模拟。 例如，Tobushi 和Tanaka[1]基于Tanaka 的一维热力学本构模型[2]模拟SMA 弹簧的力-位移关系，其研究中只考虑了弹簧丝截面上的扭矩。 结果表明，在位移幅值较小的情况下，该方法的模拟效果较好。 Liang 和Rogers[3]在先前工作[4]的基础上，提出一种简便的非线性SMA 弹簧模型，并给出了更准确的SMA 弹簧的设计方法。Toi 等[5]采用Brinson 提出的一维本构模型[6]，考虑弹簧丝截面的扭转变形，对SMA 弹簧进行模拟，并进行了有限元分析，通过和实验的比较，验证了方法的有效性。 Aguiar 等[7]采用剪切形式的一维本构模型[8]对SMA 弹簧进行模拟，假设相变在SMA 丝中是均匀发生的。 结果表明其建立的模型可以较为准确地描述SMA 弹簧的力学行为。 Mirzaeifaret[9]比较了基于Boyd-Lagoudas 本构模型[10]的直杆扭转模型和曲杆扭转模型，模拟了SMA 弹簧的力学行为。 结果表明，曲杆扭转模型的模拟结果较好。 Enemark等[11]在修正的Lagoudas 模型基础上，同时考虑弹簧丝截面上的扭矩和弯矩，建立SMA 弹簧模型，并进行了验证试验。 Savi 等人[12]通过实验和基于Auricchio模型[13]的有限元方法，研究了几何非线性对SMA 弹簧力学行为的影响。 结果指出，当弹簧指数较大时，几何非线性效应的影响较为明显。 上述研究表明，基于现有的热力学本构模型对SMA 弹簧的力-位移关系进行模拟是可行的。 最近，黄斌等[14]对Motahari和Ghassemich[15]提出的SMA 多段线性本构模型进行修正，并利用修正后的模型模拟SMA 弹簧在复杂加载条件下的力-位移关系，试验和模拟结果表明，该修正模型的模拟方法较原模型更准确。 Zhang等[16]基于Graesser-Cozzarelli 本构模型[17]，同时考虑弹簧丝截面上的扭矩和弯矩的影响，对SMA 弹簧的力-位移关系进行模拟。 其模拟结果较好，同时还研究了弹簧指数和弹簧初始高度对SMA 弹簧力-位移关系特性的影响。

目前建立的SMA 弹簧力-位移关系所使用的本构模型大多为一维本构模型，将弹簧丝截面上的正应力和切应力单独考虑，忽略了正应力和切应力之间的耦合效应。 另外，同时考虑弹簧丝截面上的扭矩和弯矩对弹簧力-位移关系影响的研究也还有待深入。笔者采用SMA 的三维热力学本构模型，同时考虑截面上的扭矩和弯矩，结合弹簧理论，对SMA 弹簧的力-位移关系进行模拟，建立了SMA 弹簧在拉伸荷载下的力-位移关系数值仿真模型。 此外，通过编写通用有限元软件Abaqus 中的用户材料子程序(UMAT)对SMA 弹簧进行有限元实现。 最后，通过NiTi 合金丝的材料试验和SMA 弹簧的多级加载试验，验证了文中所用方法的有效性和正确性。

1 SMA 弹簧拉伸试验

本文试验采用的材料为NiTi 合金丝，通过工厂加工制得NiTi 弹簧，如图1(a)所示。 弹簧丝半径为0.74 mm，弹簧圈半径为6.3 mm，有效圈数为6 圈，弹簧的初始长度为21.5 mm。 使用合适的夹具将弹簧试件固定在MTS 858 试验机上，如图1(b)所示。 试验加载采用位移加载模式，加载速度为1 mm/s，试验环境温度为27 ℃。 试验的加载工况为不同位移幅值加载，位移幅值分别为40 mm、50 mm、60 mm、 70 mm和80 mm。

图1 SMA 弹簧拉伸试验

为了获取SMA 材料相关参数，需要对SMA 丝材进行不同应变幅值拉伸卸载试验。 取同一批次的Ni-Ti 合金丝在MTS 858 试验机上进行低应变率(5×10-4s-1)和低应变幅值(2.2%，3.2%，4.2%，5.3%，6.3%)的拉伸卸载试验，拉伸试样的总长度为78 mm，标定长度为38 mm。

2 SMA 的本构模型

在小变形框架下，将材料点总应变张量ε 分解为三个部分，即弹性应变张量εe、热膨胀应变张量εT和相变应变张量εtr，即:

弹性应变张量εe和应力张量σ 的关系可以通过胡克定律得到:

式中:C(ξ)是四阶的弹性张量；εT可以表示为:

式中:α 和Tr分别是二阶热膨胀张量和参考温度。

参考Lagoudas 和Entchev[18-19]的工作，相变应变张量的率tr可以写成:

以及马氏体相变方向张量Ntr可以写成:

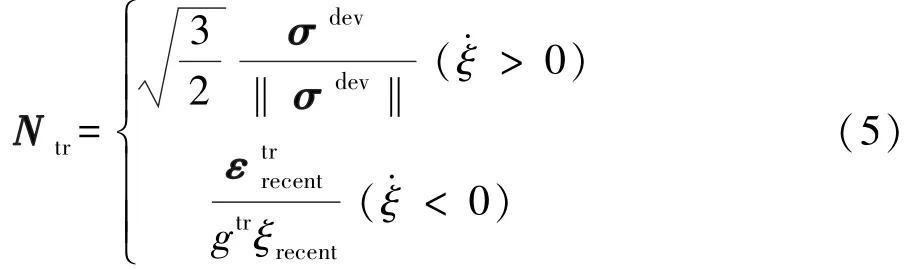
式中:是马氏体体积分数率；gtr是马氏体完全相变所造成的相变应变大小；σdev是偏应力张量；ξrecent和分别是逆相变开始点的马氏体体积分数和相变应变张量。

参考Yu 等[20]的工作，在连续介质热力学框架下，建立了材料点的Helmholtz 自由能，并通过不可逆热力学推导，得到了热力学驱动力πtr，即:

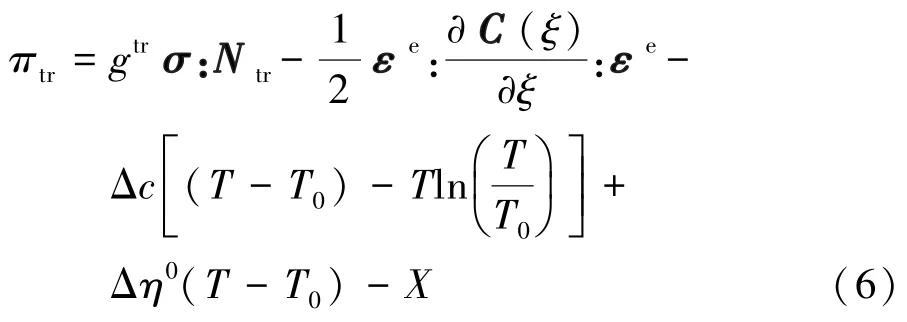
式中:Δc＝cM-cA，；cA和分别是参考状态下奥氏体的定容热容和组态熵；cM和分别是参考状态下马氏体的定容热容和组态熵；T0是平衡温度；X是相变各向同性抗力。

为便于数值实现，参考Anand 和Gutin[21]的工作，采用幂律形式的方程描述马氏体体积分数的演化:

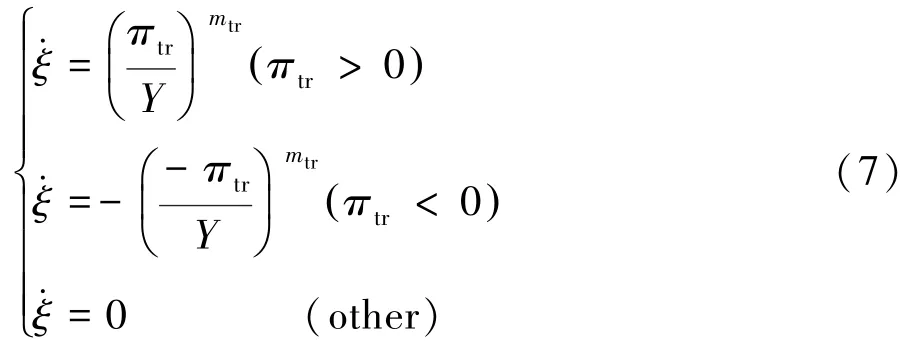
式中:mtr是材料参数，用来控制黏性大小，当mtr趋于∞大时，黏性效应消失，即退化为无黏性情形；Y是一个控制应力-应变曲线相变滞回环宽度的变量。

参考Yu 等人[20]的工作，对Y进行如下改进:

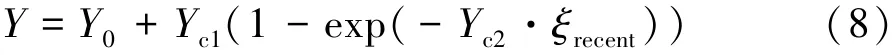
式中:Y0、Yc1和Yc2为材料参数，由此可以描述逆相变开始时的马氏体体积分数对滞回环宽度的影响。

另外，对相变各向同性抗力的逆相变部分进行改进:

式中:h1、h2和n为材料参数；变量ξrela用来刻画逆相变开始时的非线性部分，它与逆相变开始时的马氏体体积分数相关，可以表示为:

在引入应力平衡方程和变形几何方程后，结合上文给出的本构方程，可以得到描述SMA 应力-应变关系的封闭方程组。

3 SMA 弹簧的建模

当SMA 弹簧发生较大的轴向变形时，弹簧丝截面上除有扭矩的作用外，也有较大的弯矩，文中将同时考虑弹簧丝截面上的扭矩和弯矩的影响。 当SMA弹簧的圈半径和丝半径的比值较小时，由于弹簧丝的弯曲效应，在弹簧发生变形的时候，弹簧丝截面将会发生畸变，导致截面上的应变分布不再对称。 但Mirzaeifar 等[9]发现，这种效应对SMA 弹簧的力-位移关系的影响不明显，为简化分析，这里不考虑这种效应的影响，认为截面上的应变分布是对称的，如图2 所示。

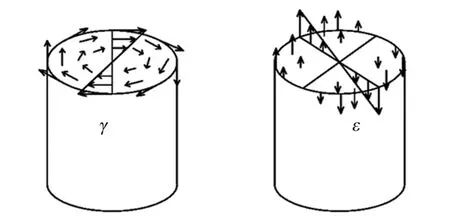
图2 弹簧丝截面切应变γ 和正应变ε 分布图

假设SMA 弹簧的初始圈半径为R0，初始长度为L0，弹簧初始螺距角为α0，弹簧有效圈数为N，弹簧丝的半径为r，弹簧在轴向力F下的纵向位移为u，弹簧变形后的螺距角和圈半径分别为α和R，如图3 所示。利用图3，弹簧丝的总长度可以表示为:

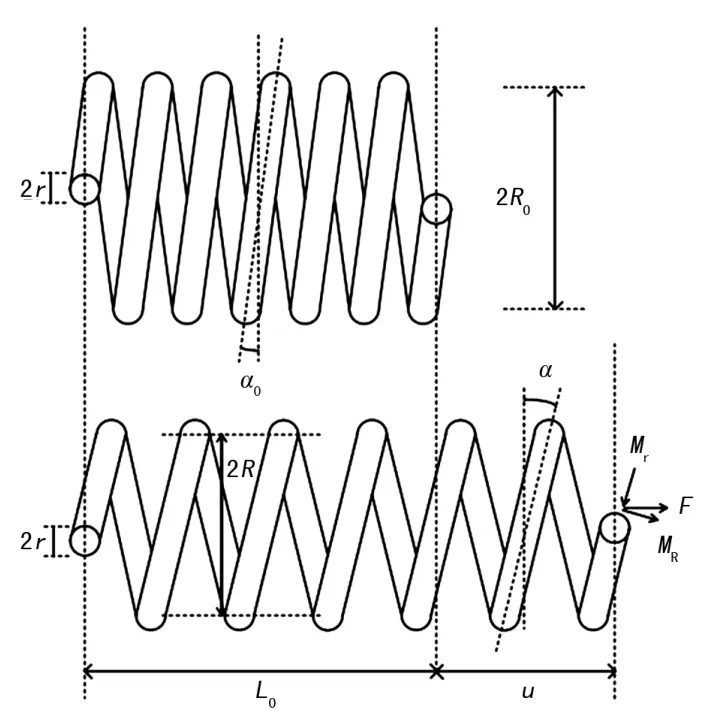
图3 SMA 弹簧受拉示意图

则弹簧的初始螺距角可以写为:

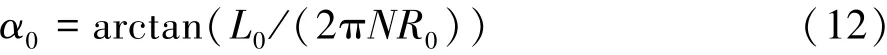
弹簧变形后的螺距角和圈半径分别为:

因此，图2 中弹簧丝截面上分布的正应变和切应变具体可以表示为:

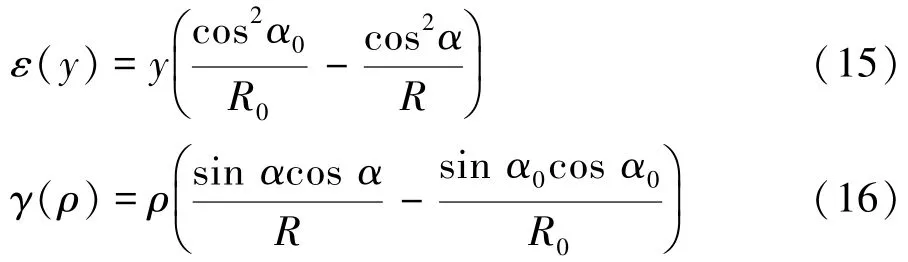
式中:ρ为极坐标系中的径向坐标；y为笛卡尔坐标系中垂直于弹簧中心轴的纵坐标。

在利用式(15)、(16)得到弹簧丝截面上分布的切应变和正应变后，结合第2 节中介绍的SMA 本构模型，可以获得弹簧丝截面上分布的切应力和正应力。 然后，可以通过如下两个积分式得到弹簧丝截面上的扭矩MT和弯矩MB:

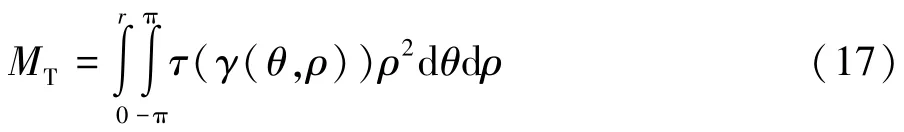
式中:θ为径向坐标；ρ所对应的角坐标。

最后，从图3 中可以发现，弹簧沿长度方向的纵向力F是由弹簧丝截面上的扭矩MT和弯矩MB共同引起的，其表达式为:

根据以上步骤，就可以得到SMA 弹簧的力-位移关系。

4 SMA 弹簧的数值模拟

由SMA 材料试验，可以得到文中所需的相关材料参数。 根据材料参数，对弹簧试件的力-位移试验曲线进行数值模拟和有限元分析，所需的SMA 弹簧试件参数如表1 所列。

表1 SMA 弹簧相关参数

首先，采用第2 节中提出的本构模型对材料应力-应变关系进行模拟。 如图4 所示，在加载过程中，模拟结果与试验完全吻合；在卸载过程中，模拟结果很好地描述了滞回环与应变幅值的关系，以及逆相变开始时的非线性段，由此验证了上述本构模型的正确性。

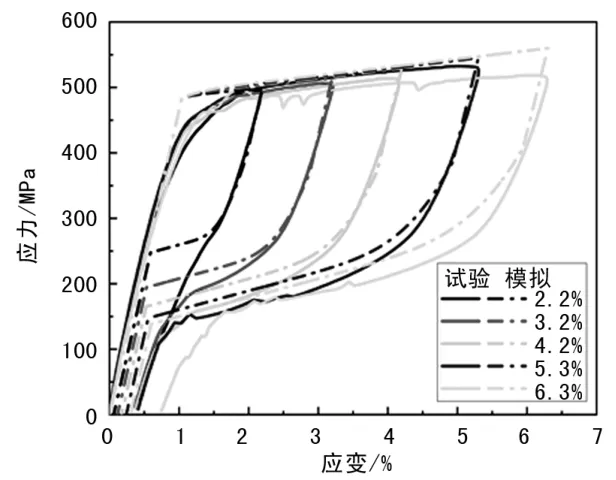
图4 SMA 材料试验及其模拟

然后，根据SMA 材料参数，对SMA 弹簧试件的力-位移试验曲线进行数值模拟，控制与试验相同的工况进行加载，模拟结果和试验结果的对比如图5 和图6 所示。

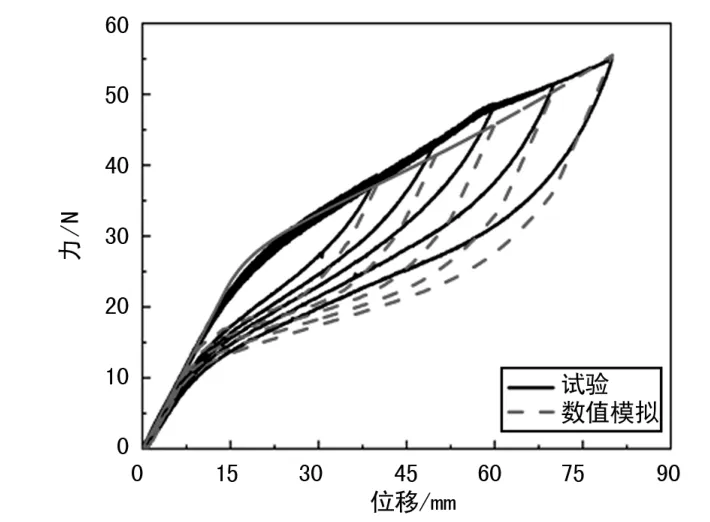
图5 SMA 弹簧考虑截面弯矩的模拟与试验结果

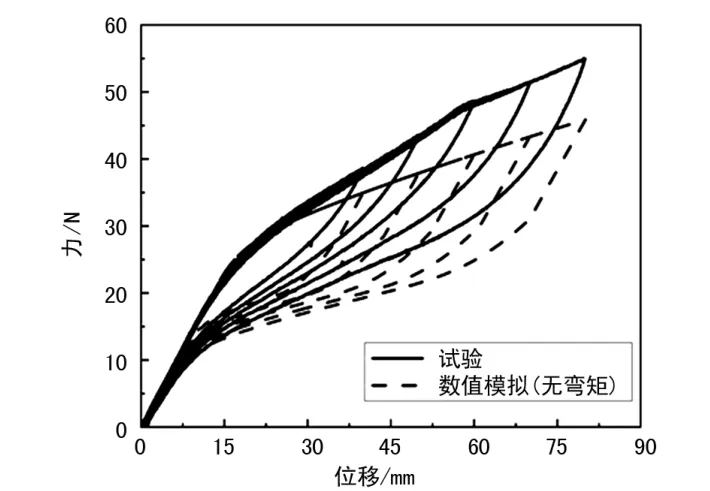
图6 SMA 弹簧不考虑截面弯矩的模拟与试验结果

从图5 中可以看出，在同时考虑了弹簧丝截面上扭矩和弯矩的模拟结果中，与试验结果较为吻合，模拟结果较为准确地描述了SMA 弹簧在拉伸卸载过程中的相变开始点，逆相变开始时的非线性段，以及滞回环随着位移幅值的增大而变大的现象。

从图6 中可以看出，不考虑弹簧丝截面弯矩的情况下，SMA 弹簧的模拟结果与试验结果差距较大，误差主要发生在SMA 弹簧开始相变之后。 位移幅值越大，其模拟结果的误差越大。 这里主要的原因是，当弹簧位移幅值增大，在拉伸过程中，弹簧的螺距角变大，使得截面上的弯矩增加，导致长度方向上的力增大。 所以位移幅值越大时，弹簧丝截面上弯矩的影响就会越大。

5 有限元分析

将2 节中提及的本构模型通过隐式欧拉法进行数值离散，并编写有限元软件Abaqus 中的用户材料子程序(UMAT)，对弹簧的变形行为进行有限元分析。SMA 弹簧的几何模型及其网格划分如图7 所示。 将SMA 弹簧下端固定，上端施加位移荷载，得到SMA 弹簧拉伸至位移幅值时的马氏体体积分数云图，如图8所示。 从图8 中可以看出，在远离施加荷载的位置，沿弹簧丝长度方向，马氏体相变是均匀发生的。 在SMA 弹簧丝截面上，弹簧的内侧先发生马氏体相变，靠近外侧的则稍后。

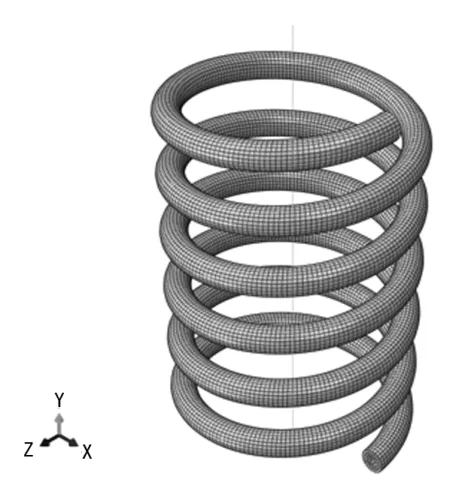
图7 SMA 弹簧几何模型及网格划分

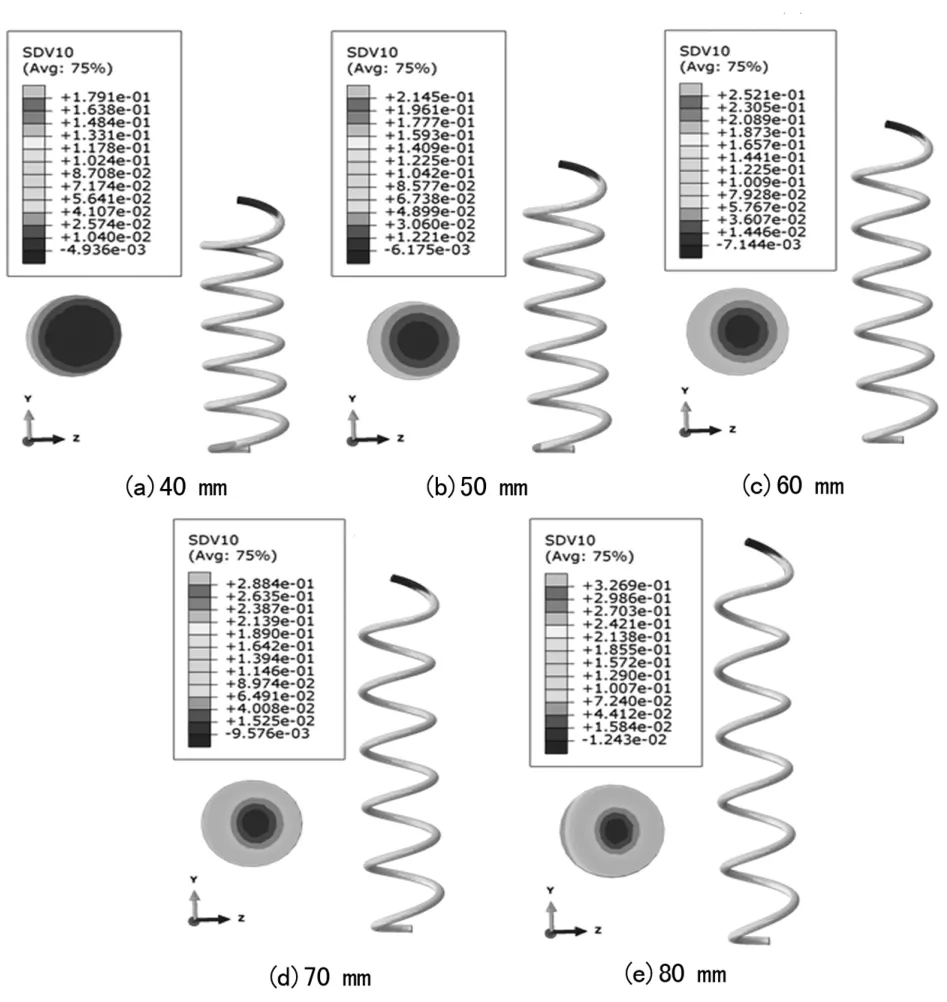
图8 SMA 弹簧马氏体体积分数分布云图

提取力-位移关系曲线，如图9 所示。

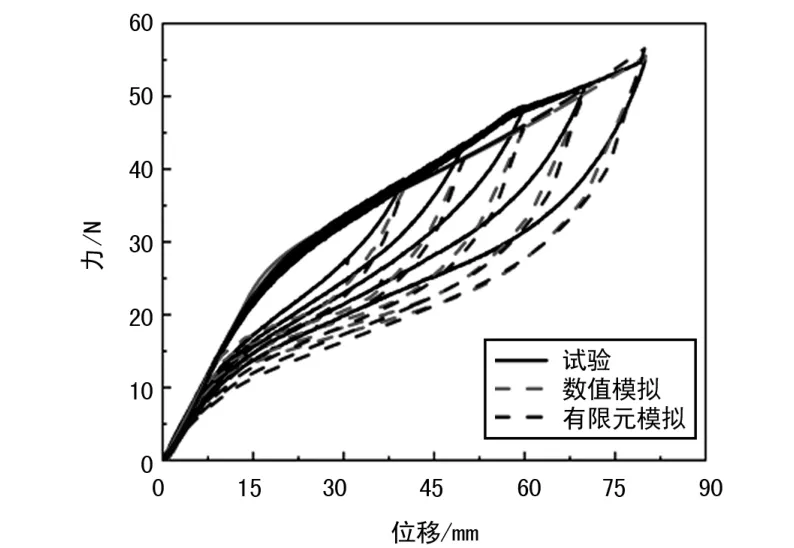
图9 SMA 弹簧试验、数值和有限元模拟结果对比

由图9 可以看出，数值模拟和有限元模拟都很好地描述了SMA 弹簧在拉伸卸载过程中的变形特性。在位移荷载施加到18 mm 左右时，SMA 弹簧开始进入相变。 从试验结果和模拟结果来看，文中所分析的几个工况中，SMA 弹簧均未发生完全相变。 在卸载后，位移减小至0，弹簧恢复至初始时无变形的状态。

由此，试验和模拟的结果充分说明了上述方法的有效性和正确性。

6 结 语

文中采用三维的SMA 本构模型，参考已有的工作，对滞回环宽度和逆相变中的相变抗力进行适当改进，并结合弹簧理论，建立SMA 弹簧力-位移关系模型，模拟结果很好地描述SMA 弹簧的变形特性。 此外，建立了对应的SMA 弹簧有限元模型，讨论了马氏体体积分数在弹簧丝截面上的变化情况。 通过NiTi弹簧试件的多级加载试验，验证了文中方法的有效性和正确性。 文中考虑弹簧丝截面弯矩的影响，通过对比模拟和试验结果发现，在弹簧变形中，弹簧丝截面弯矩会影响弹簧的力-位移关系曲线，且其影响会随着弹簧位移幅值的增加而增大，故在进行弹簧力-位移关系的研究时，考虑弹簧丝截面弯矩的影响可以使结果更加准确，更符合实际。