基于改进BAS-BPNN的Stewart平台位姿正解
2022-11-28王淑良赵明伟刘丽俊
王淑良,朱 浩,赵明伟,2,刘丽俊,2
(1.江苏师范大学电气工程及自动化学院,江苏徐州 221116; 2.上海大学机电工程与自动化学院,上海 200444)
Stewart平台属于六自由度并联机构,主要由上平台、下平台以及6个可伸缩的驱动杆组成,从机构学的角度讲,并联机构具有高刚度,并具有精确的定位能力,其高水平并联设计产生了优于串联机构的负载能力、动态性能和定位精度[1]。并联机构已在飞行模拟器以及各种驾驶模拟器、新型机床、航空航天对接等领域得到了广泛应用[2-4]。
Stewart并联机构运动学正解需要求解一组强耦合非线性方程组,目前缺乏求解运动学方程的有效算法[5]。传统的正解方法分为数值法和解析法:数值法核心为迭代计算,一般以Newton法为基础,通用性好,求解稳定精度高,但是其为局部收敛,对初始值敏感,初值选取不当容易出现不收敛[6];解析法通过建立约束方程、消元和几何分析等方法建立了几种特定结构并联平台的封闭解,虽可以求得机构全部运动学正解,但是计算过程极为复杂,缺乏通用性[7]。为了解决Newton-Raphson对初始值敏感性的问题,很多学者提出了解决方案,WANG等[8]采用自然坐标的方法得到一组二次方程的Stewart平台的运动学模型,利用此特性简化了Newton-Raphson算法,以减少方程和雅可比矩阵之间迭代的更新时间;谢志江等[9]提出了基于最速下降法和多元牛顿法的组合数值方法,在降低对初始值依赖的同时还减少了单步迭代的计算量乃至更快速的收敛。
近年来,学者们开始借鉴智能算法解决位置正解问题,以此弥补传统运动学正解算法的缺陷。很多研究者采用遗传算法[10]、模拟退火算法[11]、人群搜索算法[12]等来求解位姿正解,取得了一定的成果。BP神经网络对非线性映射有非常好的逼近能力,无需推导输入、输出的显性表达式并且运算效率高[13],但是单一的BP神经网络容易陷入局部最优,很难满足平台正解的精确要求。众多学者基于该算法进行了改进。李晶[14]采用遗传算法(GA)优化RBF神经网络模型,验证了遗传神经网络正解法具有较好的收敛性和较快的速度,能够满足Stewart平台运动学求解的需要;LI等[15]采用全局搜索能力更好的粒子群算法(PSO)对BP神经网络模型进行学习训练,训练时间更短,求解精度更高,易于实现Stewart平台的实时控制。与GA和PSO不同,天牛须搜索算法(BAS)是单体搜索算法,能够大大减少运算量和时间[16]。
本文基于BAS具有一定的精度和快速的寻优能力,对BAS的步长调整和引入惯性权重进行改进,验证改进后的BAS优化BP神经网络模型对求解Stewart平台正解具有高精度和运算速度的优越性,以解决平台正解需要的准确性和实时性问题。
1 运动学反解模型
本文研究的Stewart平台的上、下平台通过虎克铰与电动缸的两端相连,通过6个电动缸的协调运动,可以实现3个方向的位置移动和姿态转动。运动学反解是通过并联平台的位置和姿态,求各个电动缸长度的过程。定义平台坐标系,以上平台中心O1和下平台中心O分别建立动、静坐标系,上平台的位姿由动坐标系相对于静坐标系的广义坐标表示,位姿由6个参数x,y,z,α,β,γ表示,x,y,z分别表示上平台沿X,Y,Z轴移动的平移量,α,β,γ分别为横滚角、纵摆角、偏航角,表示上平台绕X,Y,Z轴旋转的角度。
采用n+1维向量来描述n维向量再进行坐标变化,如空间坐标系中某点P通过四维向量(xp,yp,zp,1)表示,平移变化矩阵为Tp,绕三轴旋转变化的矩阵为Tx,Ty,Tz,动坐标相对于静坐标系的旋转变换矩阵T=TxTyTzTp表示为
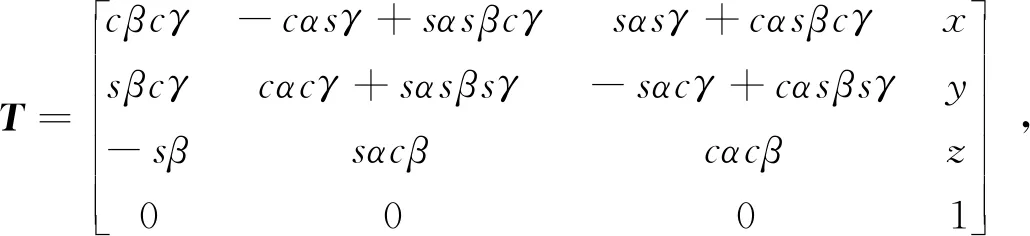
(1)
式中:cα=cosα;sα=sinα。
Stewart平台的上平台铰点为P1-6,下平台铰点为B1-6,上平台半径为Ra,下平台半径为Rb,上平台铰点夹角为2a,下平台铰点夹角为2b,平台的主视图和俯视图分别如图1 a)和图1 b)所示。
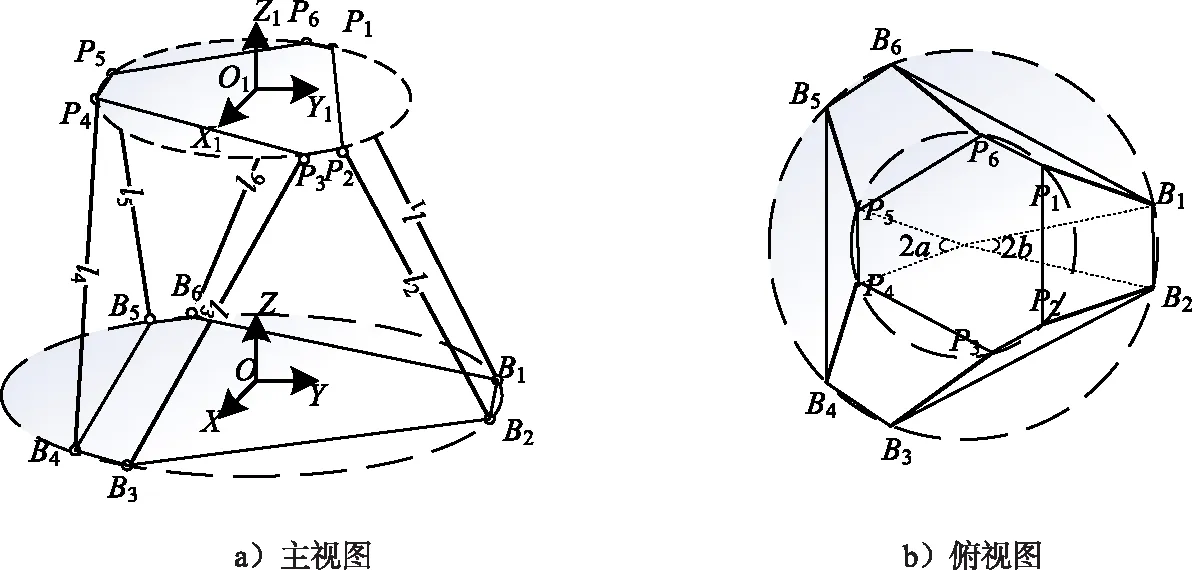
图1 平台示意图
根据平台的空间向量关系可以得到:
li=Pi+H-Bi,
(2)
式中:Pi,Bi,li分别表示静坐标系中上平台中心点到第i个上铰点的向量,下平台中心点到第i个下铰点的向量和第i个电动缸的空间向量,则上平台在初始中位时各缸的长度为|li|。当上平台运动到目标位姿时,即动平台进行平移旋转运动,图2是位姿变化示意图,空间向量关系为
li′=TPi+H-Bi,
(3)
式中TPi的结果采用3维向量表示,则变化后的各电动缸的长度为|li′|。
2 IBAS-BPNN模型的建立
2.1 BP神经网络
BP神经网络是一种反向传播网络,具有良好的函数映射能力和数据预测能力,BP神经网络通过对大量数据的训练模拟出输入数据与输出数据之间的非线性关系[17]。结构上分为输入层、隐藏层和输出层,在隐藏层和输出层中的每个神经元其净激活量为
(4)
式中:netj是指此层中第j个神经元的净激活量;xi是指神经元的输入值;ωij,θ分别表示神经元上的权值和阈值。
初始化网络的权值和阈值,对输入的参数进行正向传播,通过梯度下降法进行误差反向学习,每次迭代都对权值和阈值进行调整,以训练数据的均方误差为目标,通过迭代学习,保证误差与设定值接近后停止训练。Stewart平台有6根作动器和6个位姿参数,所以建立的BP神经网络模型有6个输入和6个输出,输入是作动器的长度,输出是平台的位姿参数。隐藏层的神经元个数参考经验公式(5),根据逐步增长或逐步修剪法反复实验来找到最合适的值[18],本文选取Q=20。同时,隐藏层选择tansig函数作为激活函数,输出层则选择purelin函数,训练函数选择trainlm函数。
(5)
式中:I,O分别为输入和输出节点个数;C为常数。
2.2 天牛须搜索算法
天牛须搜索算法(BAS)是在2017年提出的一种生物启发式智能优化算法,是受到自然界中天牛觅食原理的启发[19]。天牛须搜索算法是单体智能寻优算法,具有个体简单、计算量小、收敛速度快、全局优化能力强并且容易实现等优点[20]。在觅食过程中,天牛会通过2只触角对空间的食物气味进行感知,并且2只触角距食物的远近不同,所感知的食物气味浓度也有差别,天牛会向着浓度强的一侧随机前进,最终找到食物的位置。BAS算法中天牛的当前位置即为所求解问题的一个可行解,食物的气味浓度即为适应度函数。BAS算法的主要步骤如下。
Step1:设定2须之间的距离d0,步长为step,假设天牛的初始空间坐标为
X0=(x1,x2,...,xk)。
(6)
Step2:产生一个随机向量b=rand(k,1),并对其作归一化处理,则创建天牛左右须的空间坐标:
(7)
Step3:更新天牛下一步位置:
Xt+1=Xt-δtb×sign[f(Xl)-f(Xr)],
(8)
式中:f(X)是适应度值;sign()是符号函数;δt是第t次迭代时的步长。初始步长更新公式为
δt=eta×δt-1,
(9)
式中eta为步长因子,取值在0~1之间,一般取0.95,其作用是按比例减小步长,提高算法的收敛速度和性能。
2.3 改进天牛须搜索算法
BAS算法是一种不改变优化对象的随机优化方法,当计算成本增加时,搜索算法的实时性能将降低。因此,合理的参数初始化和更新策略可以在一定程度上提高搜索效率[20]。KOU等[21]受到WCA随机游荡行为的启发在左右触角上添加了“随机天线”,增强了局部搜索能力。
BAS算法的搜索能力和收敛速度受步长影响较大,原算法的步长策略容易过早收敛陷入局部最优,影响搜索效率和精度。本文对其步长策略进行改进,改进后的步长变化公式为
(10)
式中:δstart是天牛初始步长;δend是结束迭代时的步长;T是最大迭代次数。
通过式(10)可以看出,步长与迭代次数成负相关并且步长呈非线性减小,因此在迭代初期步长值较大且变化缓慢,有利于迭代初期找到满足条件的局部最优值,并以较快的速度遍布整个搜索空间从而确定最优值的大概范围;当接近最大迭代次数时,步长变化较快且接近迭代结束时的步长,由于此时天牛的搜索空间集中在最优值的附近,快速减小的步长能够快速收敛逼近全局最优值。
一般来说,单体搜索的能力弱于群体搜索,在单体层次上可以通过引入惯性权重Wt,增强个体的搜索能力。这一原理与添加随机天线类似,差别是惯性权重变化规律是通过人为设定的,前期较大的惯性权重值可以加快天牛对新区域的搜索速度,后期较小的权重可以增强天牛的局部搜索能力。权重更新的表达式和改进后天牛位置更新的表达式如下:
(11)
Xt+1=WtXt-δtb×sign[f(Xl)-f(Xr)]。
(12)
2.4 IBAS-BPNN模型建立
BP神经网络的初始权值和阈值一般是通过随机初始化的方式取得的,容易陷入局部最优。研究表明,使用优化算法对初始权值和阈值进行优化,很大程度上提高了BP神经网络的性能[22]。利用改进天牛须搜索算法(IBAS)的优点,可以快速搜索出网络的最佳初始权、阈值,以提高网络全局最优能力。
Stewart平台的6个电动缸的长度作为输入数据集,平台位姿的6个参数为输出数据,隐藏层有20个神经元,IBAS优化的权、阈值总数为266个,权、阈值的合集即为天牛的位置。模型采用均方误差(MSE)作为适应度评价函数来评估模型的准确性,通过迭代更新天牛位置得到最佳适应度值。IBAS-BPNN模型的结构如图3所示。

图3 IBAS-BPNN模型结构图
3 仿真结果分析
以下结果都是在Intel Core i5处理器、8G内存、64位Windows 10操作系统、MATLAB 2019a的环境下仿真得出的。
平台参数如表1所示。在平台工作空间中随机选取1 000组位姿进行反解计算得到对应的电动缸长度参数,将数据作为神经网络的训练集,在工作空间中选取1组变化的位姿作为测试集,通过测试集误差性能验证IBAS-BPNN正解法的适用性;选择GA-BPNN,PSO-BPNN,BAS-BPNN模型与改进方法进行对比,并且采用MSE,RMSE和MAPE作为误差性能指标进行评价,验证IBAS-BPNN的优越性。

表1 平台参数
3.1 IBAS-BPNN正解结果分析
在改进BAS-BPNN模型中,算法的参数设定通过反复实验确定如下:初始步长δstart为5,结束步长δend为2,2须之间的距离d0为2,最大惯性权重Wmax为2,最小惯性权重Wmin为1/2,迭代次数为100。采用均方差作为模型迭代时的适应度值,图4是IBAS-BPNN模型的最佳适应度曲线。由图4可知,在迭代接近100次时,适应度值仍然发生变化,因此,本文尝试迭代了200次,结果发现适应度值并没有很大的提升,最终为了减少运算时间,综合考虑后仍采用100次迭代为佳。
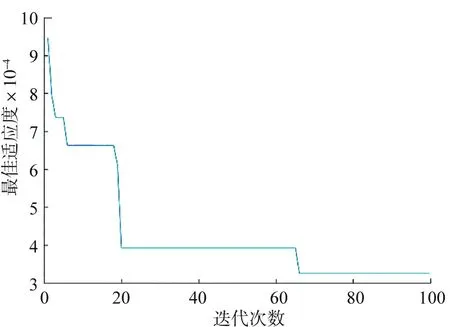
图4 最佳适应度曲线
在平台的运动范围内选取一段位姿变化作为模型的测试数据,式(13)为选取的100组位姿数据点:
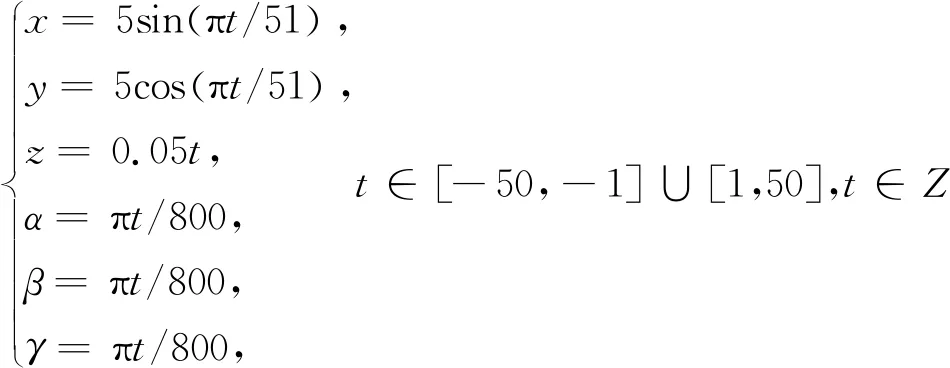
(13)
图5是这段给定位姿通过模型正解的空间位置跟踪情况,由图5可以发现该模型的正解数据能够跟踪到给定位置。但是图5无法反映平台的空间姿态,因此将6个位姿参数分为了3个位置参数和3个姿态参数,图6和图7分别是测试数据的位置误差和姿态误差。由图6可以发现,测试数据中最大位置误差仅约0.12 cm;由图7可以看出,最大姿态误差不超过0.32°。由于选取的位姿在变化到参数接近给定的极限状态时,位姿误差通常比较大,因此引入误差百分比这个指标来补充判断正解精度水平。图8是模型的误差百分比,模型的最大误差百分比不超过0.6%,并且较大误差百分比都出现在位姿参数接近于0时。由于实际位姿参数作为分母较小会导致误差百分比偏大,这也是在选取测试数据时舍去了t=0时位姿数据的原因。综上所述,IBAS-BPNN作为Stewart平台的正解方法在精度方面是满足需求的。
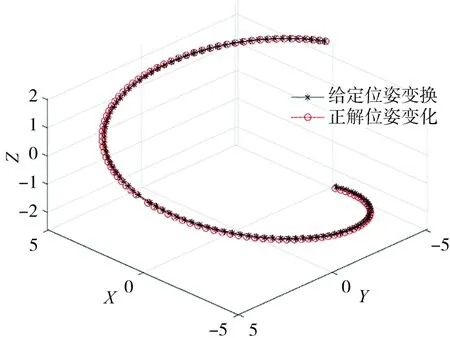
图5 空间位置跟踪

图6 位置误差
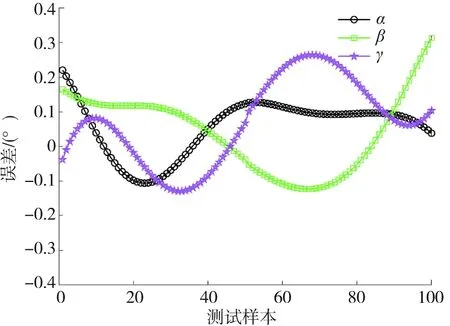
图7 姿态误差

图8 误差百分比
3.2 模型性能指标对比
为了验证IBAS-BPNN正解方法的优越性,本文在相同数据集训练,并且迭代进化次数都为100的情况下,对比了GA-BPNN,PSO-BPNN,BAS-BPNN和IBAS-BPNN模型的误差性能指标和运算时间,见表2。
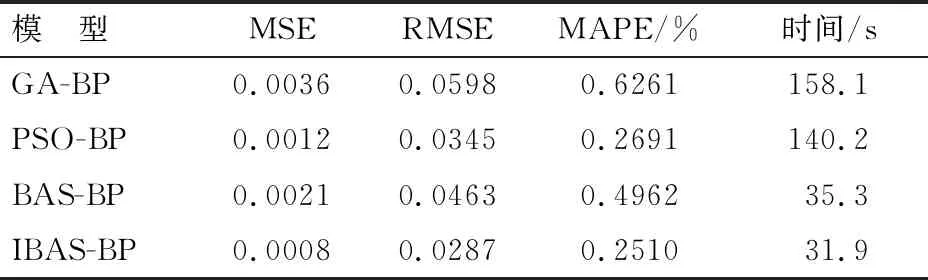
表2 模型的误差性能指标及运算时间
由表2可知,GA-BPNN的均方误差(MSE)、均方根偏差(RMSE)和平均绝对百分比误差(MAPE)都大于另外3个模型,PSO-BPNN的3个误差性能指标优于BAS-BPNN但是运算时间远大于BAS-BPNN,而IBAS-BPNN的误差性能指标相比于PSO-BPNN略有优势,并且运算时间仅需31.9 s,相较于改进前也有提升。GA-BPNN的正解精度最差且运算时间最长,IBAS-BPNN的正解精度最高且速度最快,而PSO-BPNN和BAS-BPNN在正解精度和运算速度上各有优势。
综上所述,IBAS-BPNN的正解精度和运算速度都得到了较大提升,在正解精度方面优于PSO-BPNN,在运算速度上优于BAS-BPNN,因此IBAS-BPNN模型在求解Stewart平台的正解时具有一定的优越性。
4 结 论
本文在对六自由度并联平台的运动学进行分析的基础上建立了平台的空间反解模型和优化正解模型,针对BP神经网络容易陷入局部最优的问题,提出了采用IBAS-BPNN作为平台的通用正解方法并仿真验证。结论如下。
1)通过对测试样本的位置误差、姿态误差和误差百分比分析,验证了IBAS-BPNN正解方法的适用性,其求解精度较高,解算结果稳定。
2)通过与GA-BP,PSO-BP和BAS-BP对比,验证了IBAS-BP在求解精度和训练速度方面的优越性,能够满足Stewart平台精度要求的同时兼顾求解速度的提升。此正解方法可应用于平台位姿大闭环控制、故障恢复、工作空间分析、试验过程的实时监控等场景。
在一些平台应用场景中对精度的要求非常高,本文的方法也难以满足。今后在现有工作基础上可以研究数值迭代法,将本文结果作为数值迭代的初值,探索更精确、快速的位姿正解方法。
