船舶海上航行重要航点应急保障研究
2022-11-28李成海胡甚平崔建辉
李成海 刘 杰 胡甚平 崔建辉
(1.山东交通职业学院,山东潍坊 261206;2.上海海事大学商船学院,上海 201306;3.天津理工大学海运学院,天津 300191 )
0 引 言
重要航点是指船舶水上航行途径的特殊位置海上水域,主要包括运河和海峡等。重要航点海上保障指涉及水域船舶突发事故时,重要航点应急反应能力和实施救助能力,因此海上应急保障水平是救助能否成功的关键环节。
目前针对海上重要航点应急保障具有代表性的研究成果有,李洪成等[1]采用时间函数确定模糊应急时间,用需求量度确定需求点接收资源是否满足要求。构建以系统的需求时效性、经济性、满意度和安全性多目标模型,最后,对模型求解并验证分析此方法的可行性。李国平[2]围绕服务交通强国战略、推动解决海上应急难题,推进海上交通高质量发展,建设人民满意交通运输工作。王海燕等[3]在充分分析船舶沿岸溢油应急系统影响因素前提下,构建船舶沿岸溢油应急能力评估体系,分析船舶沿岸溢油应急路径模型,并以实例计算验证模型的实用性。验证结果表明,人员保障是沿岸溢油应急的主要力量,其次是技术及物资保障。丘振文[4]工业企业对危化品具有很大需求量,所以工业企业须做好危化品周边环境调查分析工作,以此对危化品突发事件做出科学评估,并制定出应急预案,验证分析危化品周边环境风险处于可控状态。范玉改等[5]对我国卫生体系应急保障现状进行分析,提出了应对突发卫生事件的应急保障对策∶健全应急保障体系、提升应急保障能力;提高应急法治化和应急管理水平。王兵等[6]通过军民联合救援,初步形成三位一体军民融合海上应急模式,救治效果提高明显,增强了医务人员适应海上环境、锤炼专业技能,该模型成为了应急保障练兵平台。结合 26起海难突发事件救援成功经验,论证该模式为适应海上突发事故的应急救援的可行性。
本研究以重要航点为研究对象,在充分考虑重要航点应急保障影响因素间的相关性和因素分布的基础上,构建依据Sklar原理的应急保障函数模型,对重要航点应急保障进行评估,此方法解决了Copula函数参数求解复杂的难题,本研究成果可为船舶航行重要航点应急保障提供理论支持。
1 构建海上航行重要航点应急保障评估体系
1.1 影响船舶航行重要航点应急保障的因素
船舶海上航行应对突发事件的保障能力不仅与海上保障力量的实施有关,而且与保障力量实施带来的影响有关系[7]。
针对海上重要航点实施海难救助的主要机构是政府或民间组织的具有专业技能的机关,例如中国海上搜救中心,这些部门是影响船舶航行重要航点应急保障的重要力量;其次,海上利益相关国家间协同应对船舶航行重要航点突发事件,如《中国朝鲜海上搜救协议》等,共享海上应急信息,共同组织在相关海域实施的应急保障行动[8]。如果,遭遇突发事件船舶附近的船舶就近实施救助,对成功实施应急保障具有重大意义。
针对船舶海上应急保障,国际合作的法律法规是基础,如《国际海上搜寻救助公约》等。战争及国内战乱,可能对船舶航行重要航点应急保障造成重大影响甚至中断,因此船舶航行重要航点所在国政局形势也会对应急部门的应急保障产生重大影响[9]。
1.2 构建重要航点应急保障评估体系
根据船舶航行重要航点应急保障影响因素,遵循建立体系原则,构建海上重要航点评估体系,见表1。

表1 船舶航行重要航点应急保障评估体系
2 构建重要航点应急保障评估模型
根据copula函数理论,将多个联合分布的变量与“连接函数”和边缘分布的各函数的乘法结果描述其相关联关系[10]。利用降维理论,分析变量作用的少数因子有复杂关系影响因素的相关性,运用copula函数,结合选取独立因子分析,计算船舶航行重要航点应急保障水平。
2.1 分析重要航点应急保障的影响因素
2.1.1 公式化处理
(1)因为原始数据不同,需公式化处理。
增加性质指标为
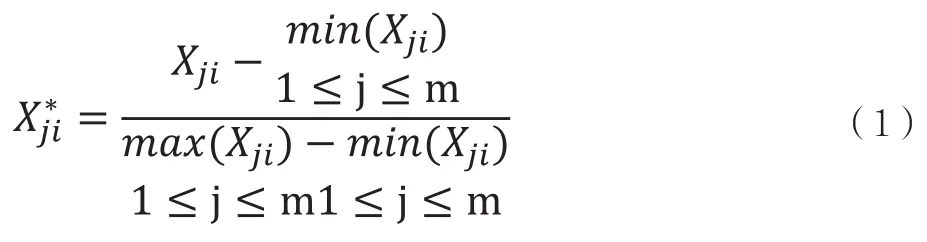
减小性质指标为

式(1)、式(2)中,Xji*代表影响因素的值;Xji代表第j个重要航点的第i个影响因素;j代表重要航点,j∈{1,2,3.....,m},m代表选择的重要航点数;i代表影响因素,i∈{1,2,3.....,n},n代表选择影响因素个数,max(xji)和min(xji)代表第i个影响因素取值的最大和最小值。
2.1.2 分析各因子间关系
运用Bartlett球形和KMO对矩阵V计算结果进行检验,并计算因子负荷和方差贡献,确定选择的因子,及各影响因素与因子间关联表达式[11]。

式(3)中,P代表因子得分值;Pji代表第j列第i个因子,共有n列m行;X表示数据矩阵;V-1表示关联矩阵的负矩阵;A表示旋回后的正矩阵。
2.2 构建海上重要航点应急保障函数模型
依据SKLAR原理,影响重要航线应急保障因素的COPULA函数表达式为:
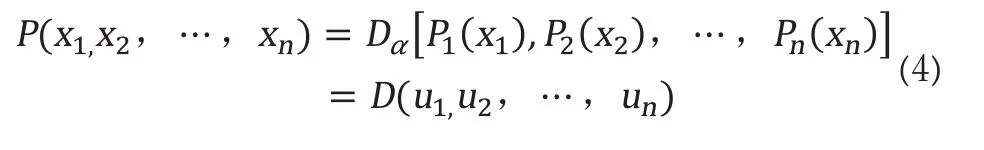
式(4)中,P(x1,x2,…,xn)表示n维联合分布影响因素变量函数;n代表变量数;D代表COPULA函数;∝代表COPULA变量函数参数;u1=P1(x1),u2=P2(x2),…,un=Pn(xn)代表因素x1,x2,…,分布的边缘函数。
根据分析因子受因素变量的影响,取得t个独立因子,与式(4)结合后,海上重要航点应急保障评估COPULA函数表达式为:
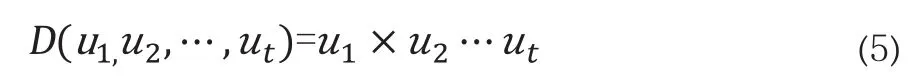
式(5)中,u1,u2,…,ut分别代表关键航点应急保障影响因素因子的分布边缘函数。
2.3 确立因子分布边缘函数
通用的线型分布有权值分布(GEV)、正态分布、对数分布和指数分布等。GEV经过FISHER理论处理后,总结出了三种极值分布[12],其标准分布函数表达式为:
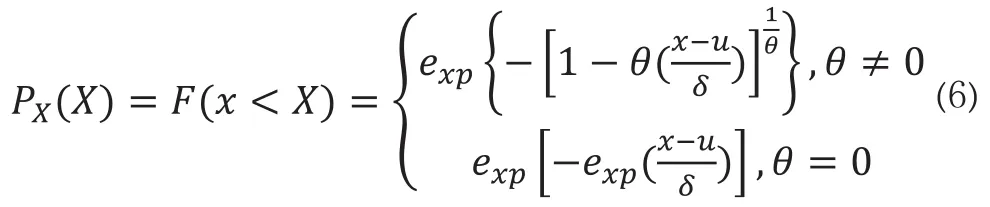
式(6)中,θ代表形状参数;u代表位置参数;δ代表尺寸参数。θ=0代表Ⅰ型极值,即Gumbel分布;θ>0代表Ⅱ型极值,即Frechet分布;θ<0代表Ⅲ型极值,即Weibull分布。
比较均方误差(RMSE)值GVNEG及信息值LBJD优选分布,利用KOLMOJOROV-SMIRNOV方法检验因子分布拟合效果,拟合效果GVNEG及信息值LBJD值越小越好[13]。

式(7)中,Cvj代表第v个因子对应第j个重要航点的频率值差,经验频率值由Gringorten公式求取,即,

式(8)中,Fe代表经验频率值等于或大于影响因素Xe,e代表计算取得的从大到小排列项数的每个因子值;根据Gringorten公式求解β取值为0.43。

式(9)中,φ代表线型分布选取的参数值。
3 案例验证分析
3.1 选取数据资料和研究对象
依据本研究选取的航行船舶重要航点涉及的相关海域国家设立的应急和保障机关,签定的国际应急协议及加入的国际公约实际情况,选取14个国际航线所经过的重要航点发生的事件进行实例验证,数据取自国际海事组织官方网站及各国海事组织官方网站。
3.2 分析因子分布结果
3.2.1 分析因子与各影响因素间的关系
通过SPSS法分析重要航点应急保障影响因素数据后,经过计算得到符合因子分析的 KMO=0.775,Bartlett<0.04。依据要求特征值>1,所以选取3个方差率累计
达83.925的因子,见表2。因子负荷矩阵中,因子与影响因素间关系,见表3。
从表2可知,FA3可解释涉及国国内形势;FA2解释应急和保障部门两大因素;FA1在船舶通行流量,国际应急合作,涉及国家数及法律法规因子负荷较大,可解释以上四大因素对船舶航行重要航点应急保障的影响[14]。
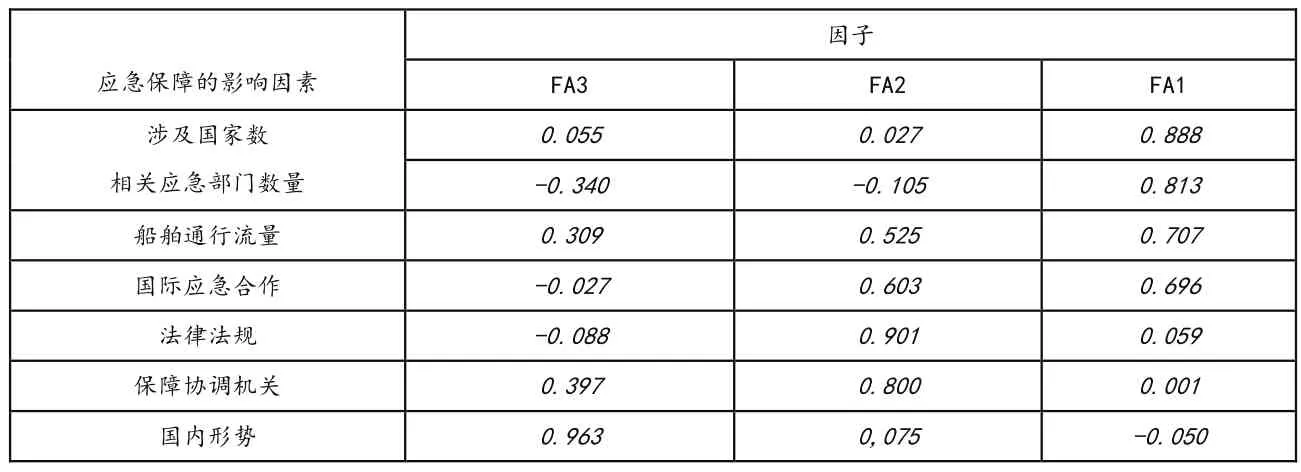
表2 因子负荷矩阵
表3中,各因子与影响因素可以对各重要航点的应急保障水平进行计算,但是没有充分考虑到影响因素的分布及特征,运用copula函数对影响因素与因子建立分布及特征的联合分布,并且不影响因子变量分布[15]。
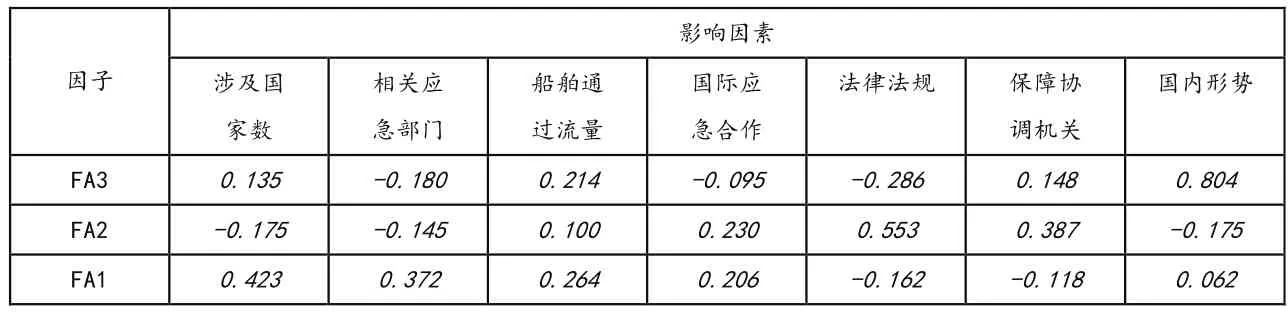
表3 因子关系式系数
3.2.2 优选因子边缘分布
选取3个因子按线型分布进行拟合处理,然后k-s检测,检测各因子边缘分布布局及对应的GVNEG和LBJD值,见表4
从表4可知,FA3检测的分布情况为正向分布和F-拓扑分布,对GVNEG和LBJD比较可看出韦布尔分布的GVNEG和LBJD值较小,所以FA3优选韦布尔分布。FA2依据F-拓扑分布的GVNEG和LBJD值较小,所以优选F-拓扑分布; FA1分布情况为正向和F-拓扑分布,比较GVNEG和LBJD值在F-拓扑分布值较小,所以FA1优选F-拓扑分布。
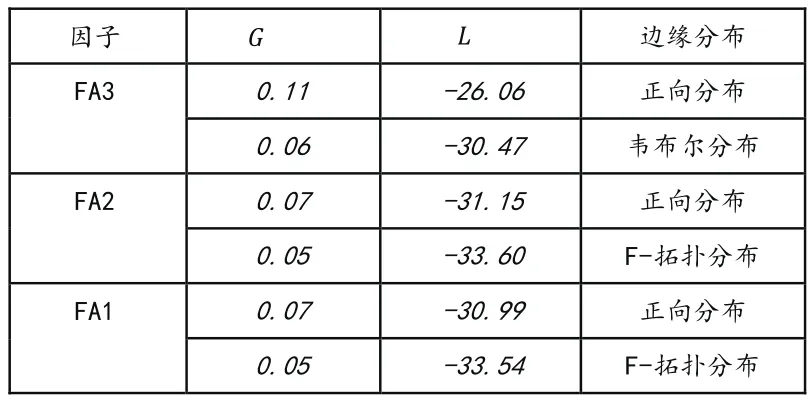
表4 因子分布拟合结果
3.2.3 船舶航行重要航点应急保障评估
结合公式(5)及优选因子分布结果,重要航点应急保障评估值表5式为:

式(10)中,u3、u2,、代表因子FA3、FA2和FA1的优选边缘分布函数,函数值大小表示应急保障水平的高低水平。
依据式(10)可得出重要航点应急保障水平,见表5;三个因子影响情况,见表6。
从表5可知,选取的14个船舶航行重要航点应急保障对比,苏伊士运河最低;马六甲海峡、土耳其海峡和巴拿马运河最高;石油重要运输通道霍尔木兹海峡应急保障评估值较大,而巽他海峡、龙目海峡作为马六甲海峡的替代航道应急保障评估值较小。
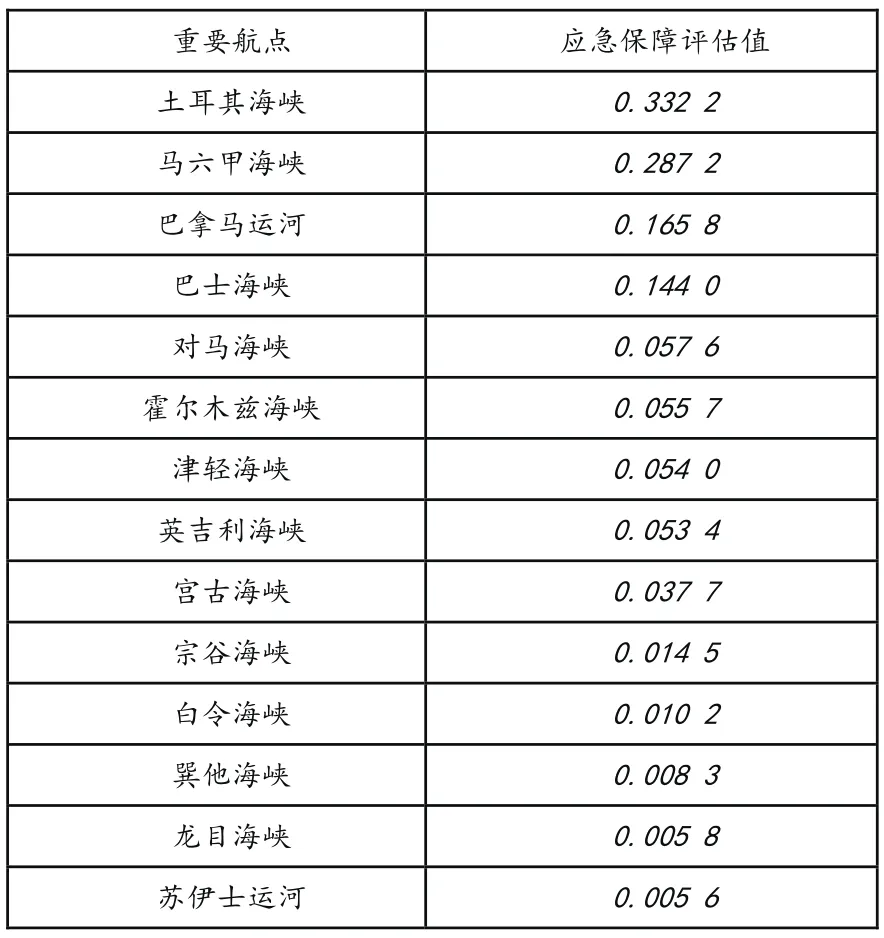
表5 船舶航行重要航点应急保障评估结果
从表6可知,FA3龙目海峡影响较小,巴拿马运河影响较大;FA2宗谷海峡影响较小,苏伊士运河影响较大;FA1对苏伊士运河影响较小,对马六甲海峡影响较大。所以,针对船舶航行重要航点应急保障各有侧重点。
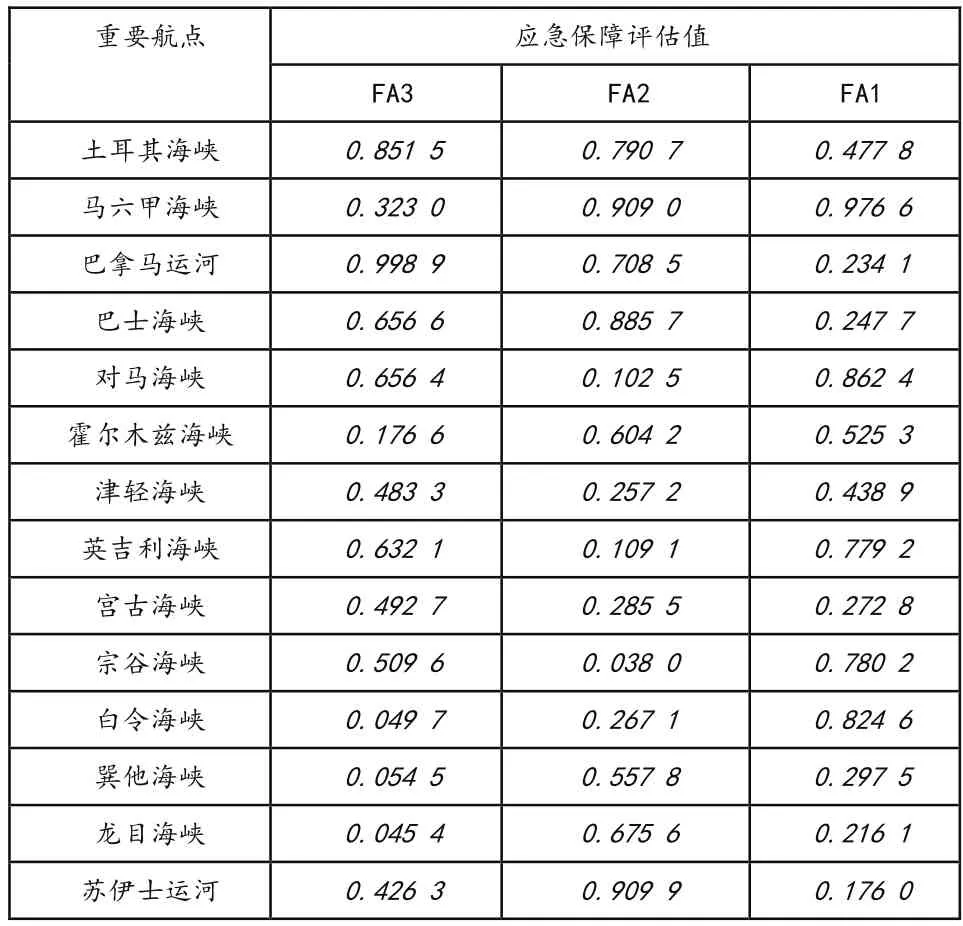
表6 因子的应急保障评估结果
从图1、图2可知,FA3和FA2联合分布及FA2分布的评估值不同,FA3和FA1联合分布评估值对马海峡最大,FA1分布评估值对马六甲海峡最大。说明因子不同的单个分布与不同因子的联合分布对评估结果的影响大小不一,因此,考虑了影响因素联合分布及边缘分布的布局,才能使评估结果更贴近现实。
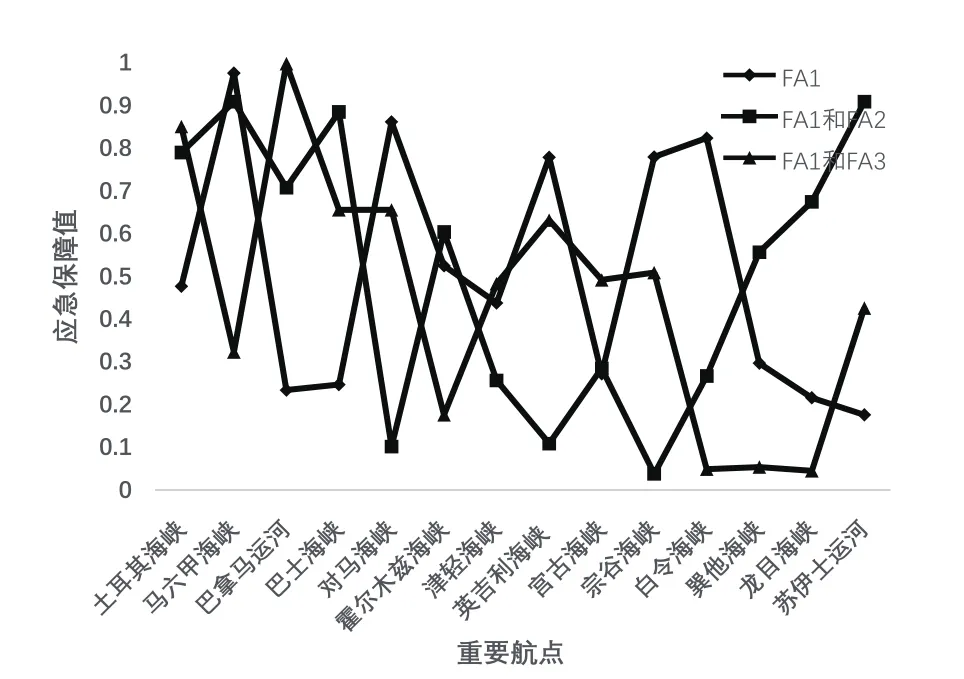
图1 FA1联合分布图
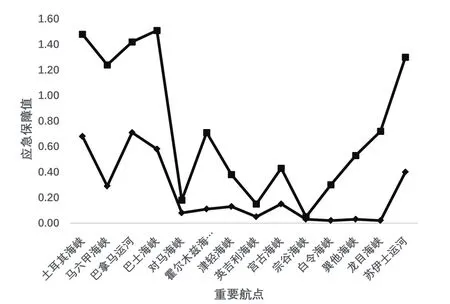
图2 FA2联合分布图
4 结 语
本研究以船舶航行重要航点为对象,充分考虑了重要航点应急保障影响因素的关联性、分布特点和变量Copula函数计算问题,建立应急保障函数模型,对14个重要运河和海峡应急保障情况进行评估。评估结果表明,重要航点应急保障苏伊士运河最差,土耳其海峡最好。通过对选取的因子单个及联合分布应急保障变化对比分析,总结出因子不同则边缘分布影响有很大差别,综合评估分析时,一定要考虑影响因素分布布局情况。此研究为船舶航行重要航点应急保障评估问题开辟了新途径,为船舶航行重要航点应急保障提供理论依据。
