基于INSGA-Ⅱ算法的武器-目标分配方法

王楠，戴江斌

(1.西安体育学院 体育教育学院，陕西 西安 710068；2.空军工程大学 空管领航学院，陕西 西安 710051)

武器-目标分配（Weapon-Target Assignment,WTA）问题是军事运筹领域的重要研究问题[1]，是根据作战体系的作战目标、平台武器配置情况，按照最优化分配原则，将不同武器分配给不同目标，从而实现最大作战效能的过程.按照不同的分类方式，WTA 问题可以划分为多种类型.按照决策阶段的划分，WTA 问题可以分为静态WTA（Static WTA,SWTA）和动态WTA（Dynamic WTA,DWTA），SWTA是在一个作战阶段将所有武器分配给目标，而DWTA 是在不同作战阶段，分批进行武器到目标的分配[2].按照决策目标的划分，WTA 问题可以分为多目标WTA 和单目标WTA，单目标WTA 是在优化过程中只有一个优化目标，而多目标WTA 有多个优化目标.按照对抗形式的划分，WTA 问题可以分为直接对抗式WTA 和间接对抗式WTA，直接对抗式WTA 是以直接消灭敌方为作战目标，目标打击对象是敌方武器平台，间接对抗式WTA 是以打击防御方资源为作战目标，目标打击对象是敌方武器平台防御的资源.

WTA 问题是一个典型的多项式复杂程度非确定性完全（Non-determinism Polynomial Complete,NPC）问题[3]，其计算难度随维度增加呈现指数级增长.对于低维度、简单约束的WTA 问题，可以采用匈牙利算法[4]、分支定界方法[5-6]和拉格朗日松弛方法[7]等.这类方法的优势在于计算方式简单，能够以较小的计算复杂度求解得到较优解甚至是最优解；但劣势在于面对中大规模问题时，方法适用性会受到一定程度影响.智能优化算法通过模拟生物智能行为，以一定的搜索策略在解空间进行寻优，具有精度高、收敛快和适用广的优势，能够用于求解高维度、复杂约束的WTA 问题.文献[8]针对存在空间约束的 WTA 问题，基于遗传算法（Genetic Algorithm,GA）进行问题求解，每个染色体被编码为具有“禁止位”的二进制矩阵进而表征问题约束，并设计了相应的交叉和变异算子 在整个进化过程中能够保证每条染色体均为 WTA 问题的有效解决方案.文献[9]以最小化幸存目标的总预期价值为优化目标建立WTA 问题模型，采用并行模拟退火算法（Parallel Simulated Algorithm,PSA）对模型进行求解，并对随机生成的12 个实例进行仿真验证，结果表明并行化计算机制能够有效提高求解效率.文献[10]以最大化目标打击效果和最小化弹药消耗、总作战时间为优化目标，考虑资源约束、可行性约束和火力转移约束等约束条件，建立了多目标多约束问题模型，并采用第2 代非支配排序遗传算法（Non-dominated Sorting Genetic Algorithm,NSGA-Ⅱ）对模型进行求解，数值模拟结果表明，NSGA-Ⅱ算法可以在有限时间内找到近似最优Pareto 前沿.文献[11]针对DWTA 求解速度慢、搜索效率低的问题，提出包含排序选择和精英引导、启发式因子等机制的改进人工蜂群算法（Improved Artificial Bee Colony,IABC），并通过不同尺度下的DWTA 求解仿真，验证了算法求解精度的优势.文献[12]以目标生存概率总期望值最小为优化目标建立问题模型，通过离散化方式，实现了WTA 问题动态-静态转换，并采用改进差分进化算法（Improved Differential Evolution,IDE）算法进行求解，并在大、中和小规模3 种场景下验证了算法的优越性.

目前已有大量关于WTA 问题的研究，本文在充分分析现有研究成果基础上，建立了间接对抗式条件下最大化目标打击收益和最小化打击弹药成本的静态WTA 双目标优化模型.针对模型特点，提出改进NSGA-Ⅱ算法（Improved NSGA-Ⅱ,INSGA-Ⅱ）进行模型求解，算法关键环节主要包括种群编码与解码方法、提高种群分布性方法、种群进化机制和约束处理机制等，并通过与其他算法在收敛性指标、均匀性指标和宽广性指标3 个性能指标上的对比，验证了INSGA-Ⅱ算法的优越性.

1 WTA 数学模型与多目标优化

1.1 WTA 问题的数学模型建立WTA 问题的要素主要包括武器和目标两大类，首先定义WTA 问题的要素种类和属性.武器平台集合记为SW={W1,W2,···,WN}，其中，N为武器平台数量，第i个武器平台Wi的载弹量为li，每个弹药成本均为ci.定义载弹量矩阵L和弹药成本矩阵C分别为：

目标集合记为 ST={T1,T2,···,TM}，其中，M为目标数量，第j个目标Tj的威胁程度为ej.第i个武器平台Wi的每个弹药对第j个目标Tj的毁伤概率为pij，定义威胁程度矩阵E和毁伤概率矩阵P为：

式中，pij表示毁伤概率矩阵中第i行第j列的元素值.

在数学模型建立过程中，需要分析模型的约束条件和优化目标.

1.1.1 模型的约束条件 主要包括单武器平台载弹量约束、目标分配弹药量约束和总载弹量约束.

（1）对于第i个武器平台Wi而言，打击目标所用弹药数量应不超过其载弹量li，即有

式中，xij表示为WTA 决策变量矩阵X中第i行第j列的元素值.定义WTA 决策变量矩阵X为：

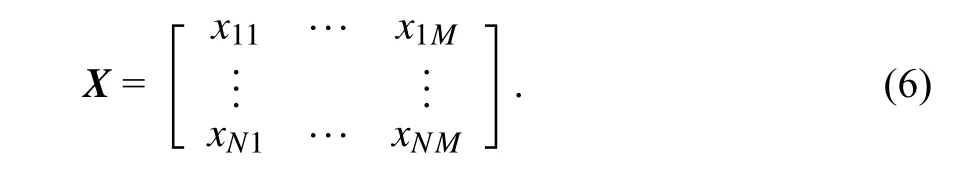
矩阵X中的行表示武器平台，列表示目标，元素0≤xij≤li表示第i个武器平台Wi分配给第j个目标Tj的弹药数量，若xij=0，则表示第i个武器平台Wi未分配给第j个目标Tj.

（2）为实现目标打击效果，对于第j个目标Tj，必须有武器平台对其进行打击；且为节约弹药量，对于第j个目标Tj，所有武器平台分配的弹药量不超过sj，即有

定义所有目标的打击弹药量矩阵S为：

（3）所有目标分配的弹药量上限值总和必须不超过所有武器平台载弹量的总和，即有

1.1.2 模型的优化目标 主要包括最大化目标打击收益和最小化打击弹药成本.

（1）对目标的打击收益通过目标的威胁程度进行度量，打击的目标威胁程度越高，消除对我方武器平台威胁的效果越好.第i个武器平台Wi对第j个目标Ti的杀伤概率为：

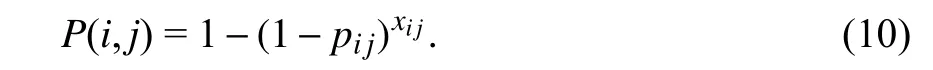
所有武器平台对第j个目标Tj的杀伤概率为：

则定义武器平台对目标的打击收益为：

（2）定义打击弹药成本为：

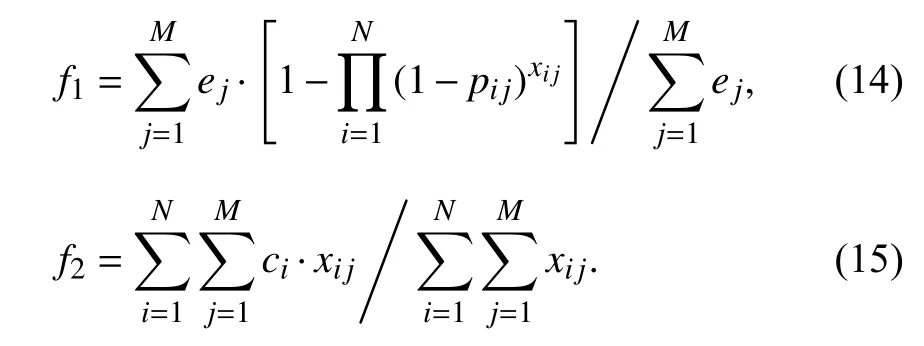
根据WTA 问题的约束条件和优化目标，可以建立数学模型为：

式中，第3 个约束是作战指挥或参谋人员根据武器平台弹药情况，对S中元素进行取值设定满足的.

1.2 多目标优化问题与Pareto 解集如式（16）所示的数学模型是典型的多目标优化问题（Multiobjective Optimization Problem,MOP），即优化目标不止1个，优化目标之间可能是不相容，甚至是冲突的.给定决策向量Y=(y1,y2,···,yQ)，若满足约束

假定有s个冲突的优化目标，定义优化目标为：

定义 1Pareto 最优解.给定多目标优化问题minf(Y)，若Y*∈Ψ，且满足式（17）和式（18），若不存在其他Y¯*∈Ψ，使得

成立，且至少一个是严格不等式，则称Y*为Pareto最优解.

定义 2Pareto 支配关系.给定多目标优化问题 minf(Y)，令Y1，Y2∈Ψ，若满足对 ∀k，1≤k≤Q，有fk(Y2)≥fk(Y1)成立，或者 ∃k，1≤k≤Q，有fk(Y2)≥fk(Y1)成立，则称解Y1支配Y2，记作Y1≻Y2.若满足对 ∀k，1≤k≤Q，有fk(Y1)≥fk(Y2)成立，或者 ∃k，1≤k≤Q，有fk(Y1)＞fk(Y2)成立，则称解Y2支配Y1，记作Y2≻Y1.若Y1和Y2互不支配，则称Y1等价于Y2，记作Y1～Y2.

定义 3Pareto 解集.给定多目标优化问题minf(Y)，定义Pareto 解集 SY*为：

2 INSGA-Ⅱ算法

NSGA-Ⅱ算法是Deb 等在2002 年提出的多目标优化算法[13]，其通过快速非支配排序、拥挤距离计算和精英保留策略等算法机制，实现了MOP 的高效求解.但是NSGA-Ⅱ算法存在解集分布性较差等问题，因此需要对NSGA-Ⅱ算法进行相应改进，即设计特定的编码与解码方式、约束处理机制等，用于求解如式（16）所示的MOP.

2.1 种群编码与解码方法在采用INSGA-Ⅱ算法求解式（16）时，需要在一定的编码空间进行.编码过程被定义为问题空间到编码空间的映射，解码过程被定义为编码空间到问题空间的映射.种群编码需遵循完备性、健全性和对应性原则，而种群解码需确保简单、快速.

在解码过程中，将所有元素向下取整，整数部分取值即为分配的目标编号.举例来说，若编码元素q4为3.137 1，整数部分为3，表示所有弹药中第4 个弹药分配给第3 个目标.解码后，通过所有解码信息可以构建WTA 决策变量矩阵X.

2.2 提高种群分布性方法传统的NSGA-Ⅱ算法在计算拥挤距离时，仅考虑相邻个体之间的距离，未考虑在不同子目标上的差异程度[14].因此，在INSGA-Ⅱ算法中，拥挤距离的计算综合考虑了相邻个体之间的距离及其在不同子目标上的差异程度，计算公式为：通过一个实际案例说明采用式（22）进行拥挤距离计算时，能够提高种群分布性.如图1 所示，为不同情况下的种群维护结果.

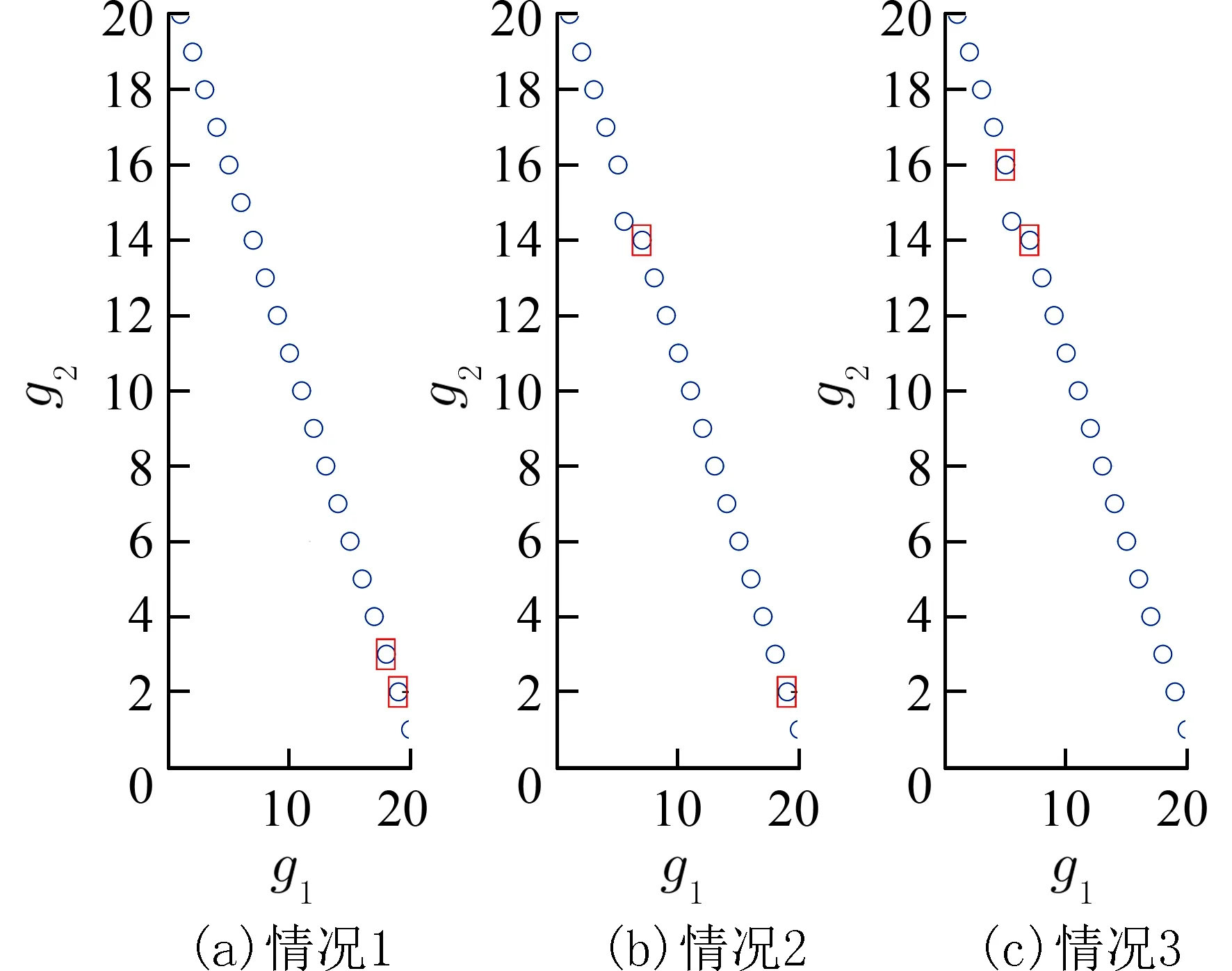
图1 不同情况下的种群维护结果Fig.1 Results of population maintenance under different conditions

在图1中，情况1 中的20 个节点构成Pareto前沿，节点横、纵坐标取值分别为1～20，间隔为1，按左上到右下顺序分别记节点序号为1～20.按照传统拥挤距离计算公式，除节点1 和20外，所有节点拥挤距离均相等，在去除拥挤距离最小的两个节点时，情况1 选择了节点18 和19.节点5、6 和7取值分别为（5,16）、（6,15）和（7,14），将节点6 的值修改为（5.5,14.5），则传统计算公式下，节点5、6 和7 的拥挤距离均不会变，因此，在去除拥挤距离最小的两个节点时，情况2 选择了节点7 和19.而在采用式（22）时，节点5 和7 的拥挤距离最小，因此，在去除拥挤距离最小的两个节点时，情况2 选择了节点5 和7.需要说明的是，修改后的节点6 应该与节点5 和7 等距，但由于图形横坐标压缩的原因，形成了如图1 所示的效果，这是正常现象.

2.3 种群进化机制采用NSGA-Ⅱ算法的进化机制，即基于多项式变异和模拟二进制交叉方法产生新个体，具体方法如下：首先，基于二进制锦标赛选择策略确定父种群；然后，在父种群中随机选取个体q1和q2，并通过产生随机数 Ξ1决定进行交叉或变异操作.

若Ξ1＜η，则进行交叉操作，产生2 个子代个体具体计算公式为：

式中，εc为交叉因子.

若Ξ1≥η，则进行变异操作，在父种群中随机选取个体q3，产生1 个子代个体，具体计算公式为：

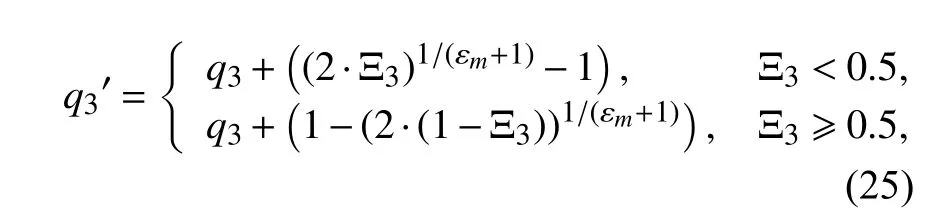
式中，Ξ3为随机数.当q的取值超出 [0,M+1-ι]的取值范围时，则取值为最近边界值.

2.4 约束处理机制实际上，式（16）中的3 个约束条件，第1 个约束条件可以通过种群编码进行满足，第3 个约束条件可以通过仿真设定进行满足，而第2 个约束条件需要采用一定的约束处理机制进行满足.对于含约束条件的优化问题，一般的处理方法主要包括强制转换、罚函数和 ε约束法等，由于式（16）所示的优化问题是一个可行解占比较低问题，主要采用强制转换方法进行约束处理.

通过以上的约束处理方式，可以生成满足第2个约束条件的可行解，从而保证算法总是在可行解空间进行搜索.

2.5 算法性能指标对于一个多目标优化算法，存在多种指标对其性能进行评价.一般而言，主要包括收敛性指标和分布性指标.

收敛性指标定义为求解得到的Pareto 解集Psol和真实Pareto 前沿Ptru的趋近程度，但对于复杂MOP，真实Pareto 前沿Ptru是不易获得的.因此，为比较两种多目标优化算法的收敛性性能，可采用一些替代方法，本文通过比较两种算法求解得到的Pareto 解集之间的覆盖率进行收敛性对比.对于的覆盖率定义为：

因此，采用如式（26）、（27）和（29）所示的收敛性指标、均匀性指标和宽广性指标作为算法性能指标，其中，收敛性指标和宽广性指标越大越好，均匀性指标越小越好.

2.6 算法流程综上所述，可以给出INSGA-Ⅱ算法的算法流程如下：

步骤 1随机初始化种群，限定种群中个体元素取值范围为 [0,M+1-ι].

步骤 2按照选择、交叉和变异操作方法，基于父种群产生一定数量的子种群.

步骤 3将父种群和子种群进行混合，并对混合种群中个体进行解码和约束处理后，得到所有个体对应的目标函数值.

步骤 4根据所有个体目标函数值的非支配等级和拥挤距离，确定精英个体为下一代种群.

步骤 5循环上述操作直至达到最大迭代次数，并输出最终Pareto 解集.

3 仿真实验分析

为验证本文算法的有效性和优越性，在处理器为Intel(R) Core(TM) i7-10 510 CPU 2.30GHz 计算机上使用Matlab 2010b 进行仿真.

3.1 仿真场景设定设定多组仿真场景，包括小规模、中规模和大规模3 种场景，每种场景的武器平台和目标数量各不相同.表1 为3 种场景下不同武器平台和目标数量组合.

表1 不同场景下武器平台和目标数量组合Tab.1 Combinations of weapon platforms and target numbers in different scenarios

载弹量矩阵L中各元素值为 3+Ξ·(6-3)」，Ξ为取值范围在(0,1)的随机数，·」为向下取整函数；弹药成本矩阵C中各元素值为 0 .15+Ξ·(0.65-0.15)；威胁程度矩阵E中各元素值为 0 .35+Ξ·(0.85-0.35)；毁伤概率矩阵P中各元素值为 0 .25+Ξ·(0.98-0.25)；打击弹药量矩阵S中各元素值为 2+Ξ·(5-2)」.为满足式（16）的第3 个约束，在生成载弹量矩阵L和打击弹药量矩阵S后均进行约束满足判断，若不满足，则循环进行生成直至满足约束.

3.2 仿真实验及结果实验1 第1 组仿真实验在典型场景取值下进行，以N=8、M=8 为例，根据实验参数设置情况，生成各参数矩阵L、S、C、E和P如下.

为验证INSGA-Ⅱ算法的改进效果，将INSGA-Ⅱ算法与NSGA-Ⅱ算法在收敛性、均匀性和宽广性上进行对比.算法参数设置方面：种群数量均设置为50，交叉概率为0.9，变异概率为0.5.如图2 所示，为INSGA-Ⅱ算法与NSGA-Ⅱ算法对比情况.

从图2 可以看出，与传统NSGA-Ⅱ算法相比，改进后的INSGA-Ⅱ算法在收敛性上要更优.而在均匀性和宽广性上，随着迭代次数的增加，INSGA-Ⅱ算法也要更优.因此，对NSGA-Ⅱ算法的改进，能够使所解保持良好分布性能.

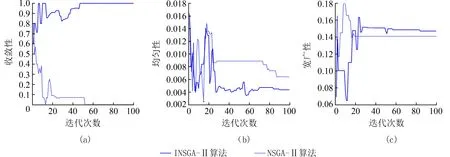
图2 INSGA-Ⅱ与NSGA-Ⅱ算法进行对比情况Fig.2 Comparison between INSGA-Ⅱ and NSGA-Ⅱ

实验2 第2 组仿真实验与第1 组仿真实验条件相似.将INSGA-Ⅱ算法与多目标粒子群算法[15,16]（Multi-objective Particle Swarm Optimization,MOPSO）、多目标人工蜂群算法[17,18]（Multi-objective Artificial Bee Colony,MOABC）和多目标人工鱼群算法[19]（Multi-objective Artificial Fish School Algorithm,MOAFSA）在收敛性、均匀性和宽广性上进行对比.算法参数设置方面：INSGA-Ⅱ算法设置与仿真实验1 相同；MOPSO 算法中的学习因子c1和c2 均设置为1.494 45；MOABC 算法的放弃阈值设置为10；MOAFSA 算法的试探次数设置为30，拥挤度因子为0.618，步长为0.1.

如图3～5 所示，为INSGA-Ⅱ算法与MOPSO、MOABC 和MOAFSA 算法对比情况.从图3 可以看出，与MOPSO 算法相比，INSGA-Ⅱ算法在收敛性和均匀性上的优势并不恒定，在某些迭代次数下更劣，但总体上更优；而在宽广性上，INSGA-Ⅱ算法优势较为明显.从图4 可以看出，与MOABC 算法相比，INSGA-Ⅱ算法在收敛性、均匀性和宽广性上均有一定优势，这体现了INSGA-Ⅱ算法相比于MOABC 算法的优越性能.从图5 可以看出，与MOAFSA 算法相比，INSGA-Ⅱ算法在收敛性和均匀性上总体占优，但在宽广性上稍劣.

图3 INSGA-Ⅱ与MOPSO 算法进行对比情况Fig.3 Comparison between INSGA-Ⅱ and MOPSO

图4 INSGA-Ⅱ与MOABC 算法进行对比情况Fig.4 Comparison between INSGA-Ⅱ and MOABC

图5 INSGA-Ⅱ与MOAFSA 算法进行对比情况Fig.5 Comparison between INSGA-Ⅱ and MOAFSA

实验3 以如表1 所示的所有武器平台和目标数量组合为例，进行第3 组仿真实验，各算法均迭代100次，分析各算法迭代一定次数后Pareto 前沿分布情况.如图6～8 所示，分别为3 种场景下各算法迭代100 次下的Pareto 前沿分布情况.

从图6～8 可以看出，除了在小规模场景N=8、M=5 情况下，INSGA-Ⅱ算法优化解并未占据明显优势，在其他场景情况下，INSGA-Ⅱ算法优化解均在Pareto 最前沿，从而验证了算法的优越性.

图6 小规模场景下各算法Pareto 前沿Fig.6 Pareto frontiers of all algorithms in small-scale scenario

图7 中规模场景下各算法Pareto 前沿Fig.7 Pareto frontiers of all algorithms in medium-scale scenario

实验4 以如表1 所示的N=8、M=8，N=24、M=24和N=56、M=56 场景为例，进行第4 组仿真实验，各算法均运行30次，每次运行均迭代100次，分析Pareto 前沿分布情况.如图9～11 所示，分别为N=8、M=8，N=24、M=24和N=56、M=56 时各算法运行30 次Pareto 前沿.从图9～11 可以看出，在N=8、M=8，N=24、M=24和N=56、M=56 场景下，INSGA-Ⅱ算法的优化效果均要优于其他算法.

图8 大规模场景下各算法Pareto 前沿Fig.8 Pareto frontiers of various algorithms in large-scale scenario

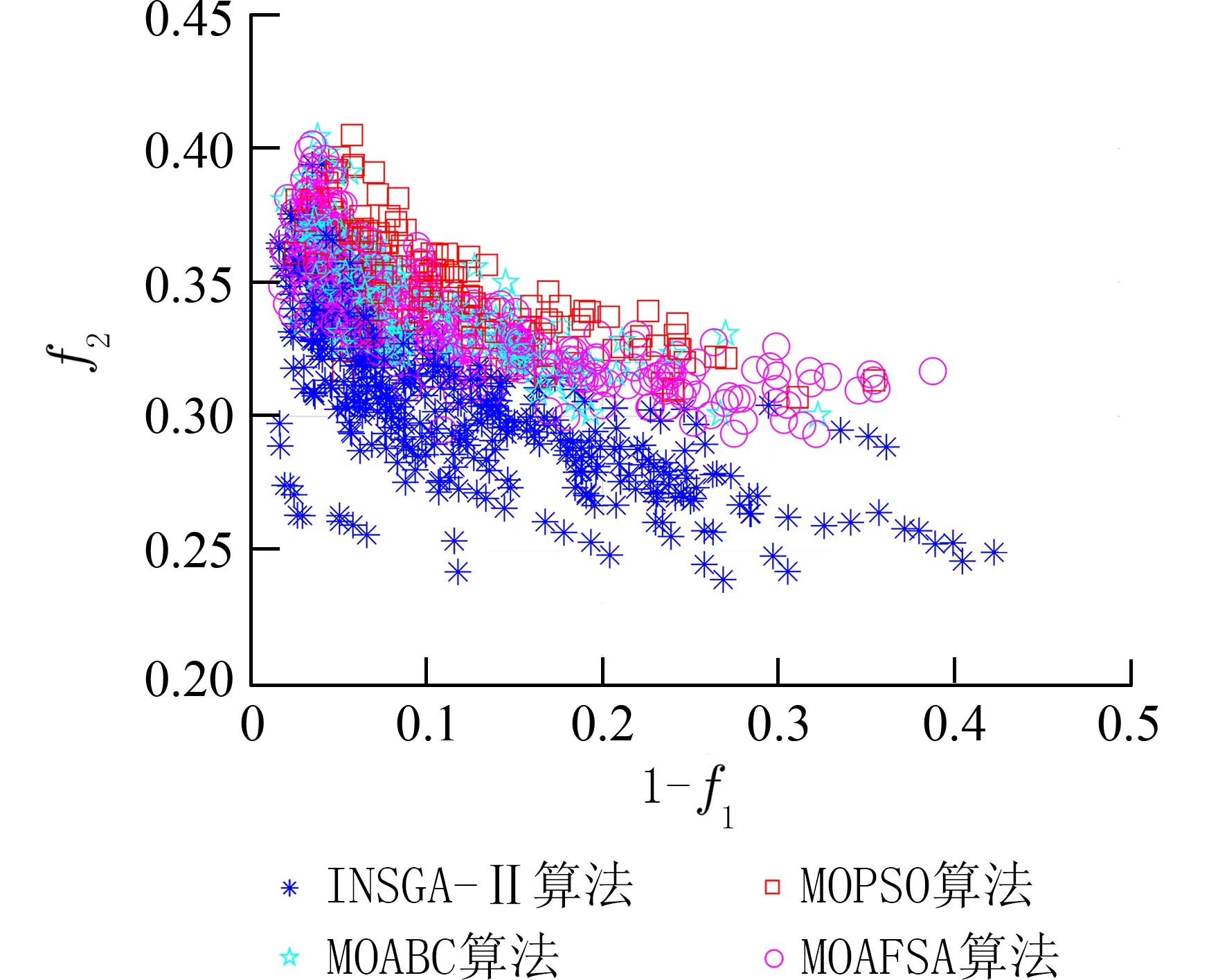
图9 N=8，M=8 时算法运行30 次Pareto 前沿Fig.9 Pareto frontier where the algorithm runs 30 times when N=8 and M=8

图10 N=24，M=24 时算法运行30 次Pareto 前沿Fig.10 Pareto frontier where the algorithm runs 30 times when N=24 and M=24

图11 N=56，M=56 时算法运行30 次Pareto 前沿Fig.11 Pareto frontier where the algorithm runs 30 times when N=56 and M=56

4 结语

针对间接对抗式WTA 问题，本文建立了综合考虑武器平台对目标的打击收益和打击弹药成本的静态WTA 双目标优化模型，约束条件主要包括单武器平台载弹量约束、目标分配弹药量约束和总载弹量约束.为求解该模型，提出包括种群编码与解码、提高种群分布性、种群进化和约束处理等方法机制的INSGA-Ⅱ算法.在仿真实验及分析方面，设置小规模、中规模和大规模3 种场景下的武器-目标数量取值组合，通过多组仿真实验验证了所提出算法的寻优能力优越性.下一步，可以考虑事件驱动的影响，对大规模场景下的动态WTA 开展研究.