基于GA－BP模型的卵石混凝土抗折强度预测

2022-11-28翟来铮高宇龙李清富

人民黄河 2022年11期

翟来铮，高宇龙，李清富，张华

（1.河南省豫东水利工程管理局，河南开封 475002；2.河南省水利第一工程局，河南郑州 450016；3.郑州大学水利科学与工程学院，河南郑州 450052）

混凝土由于具有良好的品质和低廉的价格，因此已经成为世界上最广泛的建筑材料之一［1］。混凝土构件大多是承受弯曲而不是承受轴向拉伸的，因此混凝土的抗弯拉强度能更好地反映人们所关心的混凝土性能。然而混凝土的抗拉、抗弯性能较差，在拉应力条件下容易出现裂缝，严重威胁到结构安全，因此提高混凝土的抗弯韧性具有重要意义［2］。近些年来，人们不断尝试利用辅助胶凝材料（如粉煤灰、粉状矿渣、硅粉等）来改变混凝土的性能，并取得了良好的效果，同时还可以减少废料的存量、降低混凝土的造价［3－4］。

骨料对混凝土的性能起着重要的作用，碎石是最常见的自然骨料，经济的快速发展带来了碎石骨料的短缺，并且碎石在开采过程中产生大量扬尘并污染环境，所以在卵石资源丰富的地区可用卵石来代替碎石［5］。卵石混凝土的品质也引发了人们的关注，陈代果等［6］对卵石与混凝土浆体的界面黏结强度的研究结果表明，卵石与水泥浆体的界面黏结强度仅为混凝土抗拉强度的1／3。郭勇［7］对卵石混凝土和碎石混凝土的力学性能进行了比较研究，结果表明：在相同的水灰比下，碎石混凝土的强度高于卵石混凝土的，但碎石混凝土的疲劳寿命明显低于卵石混凝土的。陈宇良等［8］研究了卵石混凝土的三轴受力性能，提出了卵石混凝土在三向受压时的相关力学指标计算公式及参数化本构方程。Ribeiro等［9］比较了碎石混凝土和卵石混凝土的断裂性能，结果表明卵石混凝土更容易破碎。但是目前对卵石混凝土力学性能的研究较少，利用有限试验数据对卵石混凝土的力学性能进行预测，将有助于在工程中实践应用。

目前，人工智能技术广泛应用于混凝土强度预测领域。梁宁慧等［10］比较了回归树、支持向量机回归和BP神经网络三种机器学习模型对高温后混凝土强度的预测精度；曹斐等［11］提出一种基于马氏距离的加权型人工智能算法对混凝土强度进行预测，并与其他机器学习模型的预测精度做了对比；Chithra等［12］分别构建多元回归分析和神经网络模型对高强混凝土进行强度预测，结果表明神经网络模型具有较高的准确性。以上研究说明了人工智能技术在混凝土强度预测领域的适用性。

伴随着环境污染问题的日益加剧以及绿色施工的迫切需求，本研究把粉煤灰和磨细矿渣作为辅助胶凝材料、把卵石作为骨料配置环境友好型混凝土，在试验的基础上，建立考虑水胶比、粉煤灰掺量、粉状矿渣掺量、砂率、卵石级配、龄期6个因素的人工神经网络模型，使用遗传算法（GA）优化传统反向传播神经网络（BPNN）模型的初始权值和阈值，比较了神经网络模型和规范公式的预测精度。

1 GA－BP模型

1.1 BPNN模型

反向传播神经网络是由鲁梅尔哈特和麦克莱兰1986年提出的，是由误差反向传播算法训练的多层前馈网络，也是目前应用最广泛的神经网络模型。BPNN由输入层、隐含层、输出层组成，每层包含几个神经元［13］，同一层的神经元互不连接，而相邻层的神经元相互连接（见图1）。

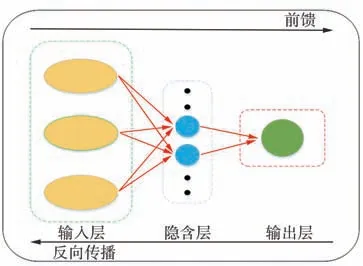
图1 BPNN模型结构

在BPNN模型中，隐含层的节点输出为

式中：n为输入层节点数；ωij为第i个输入节点到第j个隐含层节点之间的权值；xi为输入值；θj为输入层到第j个隐含层节点的阈值。

输出层的节点输出为

式中：m为隐含层节点数；Tjk为第j个隐含层节点到第k个输出层节点之间的权值；yj为第j个隐含层节点的输出值；λk为隐含层到第k个输出层节点的阈值。

f（x）为变换函数，在实际应用中常使用Sigmoid函数。Sigmoid函数的输出值在（0，1）区间，x为函数的输入值，函数形式为

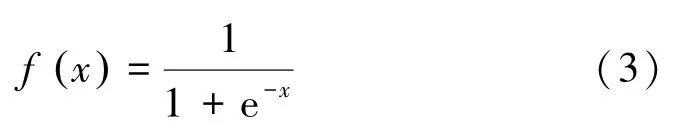
根据式（1）～式（3），输出层的输出值可以通过逐层计算输出来获得。在误差反向传播过程中，需要定义一个目标函数，这个目标函数是输出层的输出值Ok和预期输出值（实测值）之间的误差平方和：

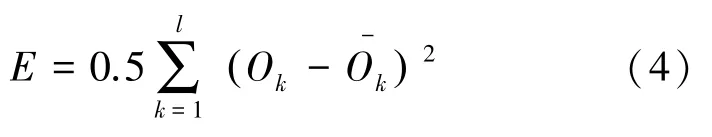
式中：l是输出层的节点数。

在误差反向传播过程中，主要通过误差函数来调整输出层的权值和输入层的权值。BPNN通过反复对权值的更新调整逐渐缩小误差，所以不断学习的过程就是对权值不断更新调整的过程。

1.2 用遗传算法优化BPNN

遗传算法是一种不受自然选择和遗传变异等进化过程启发的无梯度全局优化和搜索技术，是由美国的John Holland教授在20世纪70年代首次提出的。它不受导数和函数连续性的限制，可以直接作用于结构对象。GA算法采用概率优化方法，可以自动获取和引导优化搜索空间，自适应调整搜索方向，不需要确定规则。与传统优化算法不同，GA法允许在不同方向同时搜索最优解，而不是从一个方向开始［14］。另外，GA算法对目标函数的状态没有具体要求，具有良好的全局搜索能力。因此，GA算法可用于优化BPNN的连接权值和阈值，GA－BPNN模型算法流程见图2。

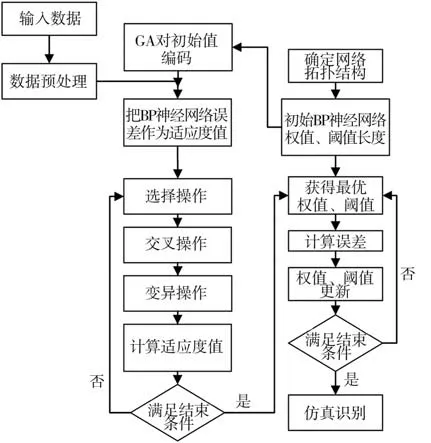
图2 GA－BPNN模型算法流程

BPNN基于梯度下降算法进行训练和权重调整。训练前，BPNN随机将每层的连接权值和阈值初始化为取值区间［14］内的值。这种随机初始化方法容易降低BPNN收敛速度，导致局部极值问题，而GA算法具有较强的全局收敛性，但局部求精能力不足，所以我们可以把GA算法和BPNN结合起来。当BPNN收敛速度较慢时，网络中各层的连接权值和阈值可以作为GA算法的输入信息，通过遗传算子得到最优个体。GA算法得到的最优个体被解码并分配为BPNN的初始权值和阈值，然后利用BPNN进行局部优化得到具有全局最优解的输出值。从基于GA算法的BPNN角度来看，该方法是利用GA算法搜索目标信息的解空间。当GA算法找到更好的网络形式时，用BPNN模型进行定位，从而找到问题的最优解。具体步骤如下［10，14］：

（1）确定初始结构。首先确定BPNN的网络拓扑结构，然后根据网络拓扑结构确定个体的长度。网络中的所有权值和阈值都被实数编码为一组染色体。

（2）确定适应度函数。将BPNN的预测输出与期望输出的绝对误差之和的倒数作为适应度函数F：

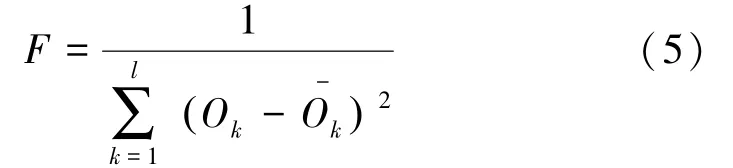
（3）进行遗传操作。本研究根据个体适应度值，采用轮盘赌法计算个体选择概率，并用单点交叉和均匀变异法进行遗传操作。

（4）解码。把GA算法输出的权值和阈值作为BPNN的初始权值和初始阈值。BPNN进行前向传播，计算全局误差，调整网络参数，并重复学习训练。

2 试验数据采集

本研究利用试验得到的96组数据组成数据库［15］，随机抽取80组数据用于训练，剩余的16组数据用于预测。水胶比、粉煤灰掺量、粉状矿渣掺量、砂率、卵石级配、龄期作为输入层的输入数据，卵石混凝土抗折强度值作为输出层的输出数据，使用MAT⁃LAB2018b来设计和测试神经网络模型。

2.1 试验材料

试验材料包括水、水泥、河砂、卵石、粉煤灰、粉状矿渣、减水剂，以及P·O 42.5普通硅酸盐水泥。根据《建设用砂》（GB／T 14684—2022）的规定，将细度模量为2.8的天然河砂作为细骨料；根据《施工用卵石、碎石》（GB／T 14685—2022），采用了2种不同级配的卵石，粒径分别为20、40 mm；按照《用于水泥和混凝土中的粉煤灰》（GB／T 1596—2017），选用一级粉煤灰；采用密度为2.88 g／cm3、比表面积为463 m2／kg的粉状矿渣。

2.2 配合比设计

在试验中，将水与胶凝材料的比例（W／B）、粉煤灰和粉状矿渣的掺量、砂率和卵石级配作为影响因素，并针对每个因素确定了4个水平等级。基于正交试验设计方法确定了16种配合比（见表1）。水与胶凝材料之比的变化范围为0.350～0.425，砂率为33%～39%，粉煤灰和粉状矿渣的掺量（质量百分比）分别为5%、10%、15%、20%；另外，卵石级配分为4个等级，小卵石（5～20 mm）和中卵石（20～40 mm）的比例（质量百分比）分别为30%∶70%、40%∶60%、50%∶50%、60%∶40%。

表1 配合比的正交试验设计 kg／m3

2.3 试验结果

将卵石混凝土在标准条件下分别养护1、3、7、14、28、45 d，不同龄期卵石混凝土的抗折强度试验结果见表2。

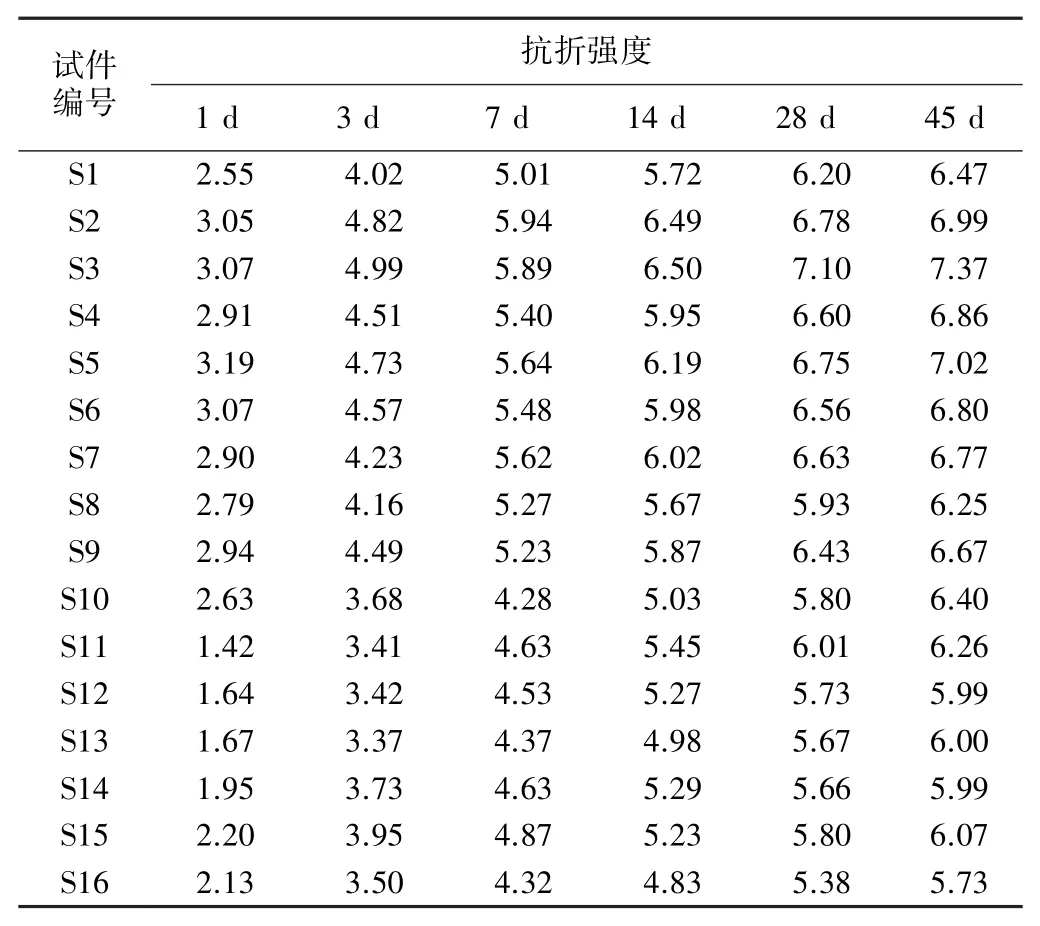
表2 不同龄期卵石混凝土的抗折强度试验结果 MPa

3 预测结果对比

3.1 模型参数设置

GA－BP（GA－BPNN）模型中，经多次试算优化，BPNN网络结构设置为6个输入层、8个隐含层、1个输出层，采用Tansig函数传递和Levenberg Marquardt函数训练，训练精度设为0.1。GA算法主要遗传参数设置为：种群规模100，交叉概率0.4，变异概率0.005；模型最大训练和迭代次数均为100。

3.2 预测结果

为了验证模型的预测精度，通过均方误差MSE和拟合优度R2来进行检验。MSE表示预测值与实测值间的离散程度，R2用于验证预测值与实测值间的拟合程度，两个指标分别由式（6）、式（7）得出：

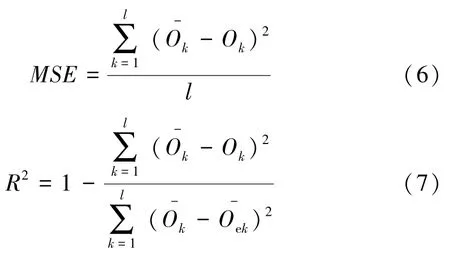
3.2.1 BPNN预测结果

图3显示了测试样本的卵石混凝土实测抗折强度与BPNN模型预测结果之间的比较。可以清楚地看到，大多数预测值和实测值间的差值都在0.5 MPa以内，这表明测量结果与模型预测吻合较好。MSE和R2作为评价指标，可以对神经网络模型的有效性进行评价，BPNN模型测试集的MSE为0.202 7、R2为0.933 7，满足要求，因此建立的BPNN模型可以较好预测卵石混凝土的抗折强度。

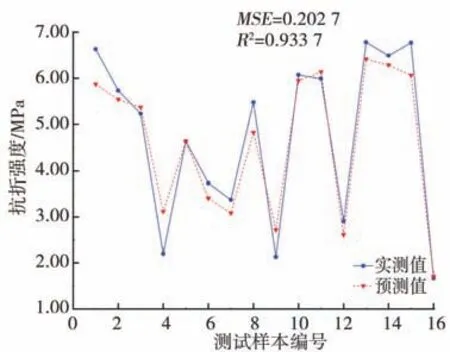
图3 BPNN模型预测结果

3.2.2 GA－BP预测结果

GA－BP模型训练测试值与实测值二者对比见图4，其相关系数达到了0.996 8、0.976 0，说明训练之后的神经网络性能良好。在测试过程中，通过训练的神经网络对混凝土抗折强度的预测值与实测值间的相关系数达到了0.976 4，测试集的MSE为0.161 5、R2为0.947 2。总体上抗折强度预测的神经网络输出值与实测值的相关性也很高，相关系数达到了0.989 4。上述试验结果表明，GA－BP神经网络模型在卵石混凝土抗折强度预测领域有较大优势和应用潜力。

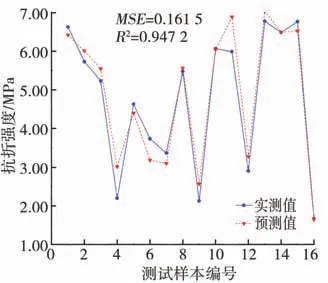
图4 GA－BP模型预测结果

3.2.3 修正后的规范公式预测结果

目前，大部分的抗折强度预测模型都是基于混凝土的抗压强度，我国现行规范中还没有建立混凝土抗压强度与抗折强度的关系；美国的ACI－318规范给出的混凝土抗压强度与抗折强度关系式为（式中：fr为抗压强度；为抗折强度）。由于试件形状和试验条件不同，该方程的适用性较低，因此根据文献［15］中的抗压强度和抗折强度数据对抗折强度系数进行修正，当R2达到最大值时的修正系数为0.86。

试验中16组数据测试结果表明修正后规范公式的大部分预测值和实测值间误差较小，只有第4个和第8个测试点误差较大，因此修正后规范公式的整体预测精度低于BPNN模型和GA－BP模型（见图5）。

图5 修正后规范公式预测结果

3.3 各种方法预测结果对比分析

神经网络模型和修正后规范公式的预测精度对比见表3。结果表明，神经网络模型比规范公式具有更高的预测精度，同时机器学习方法也可以减少试验的次数。相比之下，利用配合比参数对卵石混凝土的抗折强度进行预测是一个非线性问题，在函数取值范围内会存在多个极值，而BPNN是利用误差函数单调上升或下降来实现权值更新，所以在求出局部极值后会停止对权值的更新调整。用GA算法可以对模型的边界值和单点进行变异，从而使群体中个体不会在后续的繁衍中朝着单一化方向发展，降低网络陷入局部极值的概率，最终的连接权值会更加稳定，对抗折强度的预测精度也更高。因此，推荐GA－BP模型作为卵石混凝土抗折强度的预测工具。