发电机深调进相工况下加速功率型电力系统稳定器特性分析

梁 浩，谢 欢，王 聪，秦 川，张广韬，訾 鹏

（1. 国网冀北电力有限公司电力科学研究院，北京市 100045；2. 国家电网有限公司华北分部，北京市 100010）

0 引言

电力系统稳定器（PSS）属于自动电压调节器（AVR）的一种附加励磁控制，通过发电机励磁系统提供附加阻尼转矩，达到提高系统阻尼的作用［1-3］。PSS 原理明晰、技术成熟，已成为目前提高系统稳定、抑制低频振荡最为经济、有效的技术手段［4-7］。

目前，并网机组励磁系统广泛应用的是加速功率型PSS，如PSS2A、PSS2B，采用发电机转速和电功率作为输入信号，既能有效抑制系统低频振荡，又明显改善了PSS1A 模型在有功快速变化时的“反调”现象［8］。关于加速功率型PSS 已有大量理论研究和实践应用［8-11］。文献［8］阐述了加速功率合成环节作用的原理，具有良好的工程实用效果。文献［10］以实际机组为例，详细介绍了加速功率型PSS现场试验及参数整定方法。文献［11］提出了一种仅需1 阶超前和1 阶滞后即可满足全频段相位补偿要求的新型PSS 设计方法，从原理上解决了PSS 的低频段增益受限问题。

对于加速功率型PSS，研究的难点是转速输入信号的获取和处理，现场因转速信号通道问题导致PSS 输出异常并引发机组功率振荡的事件时有报道［12-15］。国内外主流励磁厂家装置虽然在实现算法、滤波处理等细节上各不相同，但原理上均是采用电气量计算方法，采集机组电压、机端电流以及电抗参数计算发电机q轴内电势Ėq，进而求取Ėq的角频率作为机组转速信号［16-20］。该方法相比采集机械转速无须额外配置转速测量硬件、不受传输延时以及电磁干扰影响，实现方式简单有效，目前几乎应用于所有在运机组加速功率型PSS。但针对电抗参数的取值，不同励磁厂家装置出厂默认值各不相同，一般在发电机q轴次暂态电抗Xq''和同步电抗Xq之间［16-17］。由于PSS 经过增益整定和相位补偿后在绝大多数情况下抑制功率振荡效果明显，现场PSS 试验时一般不对该电抗参数进行调整，对于该参数整定优化也一直未引起足够的重视。虽然文献［16］通过仿真对比指出电抗参数采用Xq''比采用Xq效果更好，但未开展更深入的理论研究。

随着中国电力系统向着新型电力系统方向发展，常规火电机组功能定位正从“重载运行、电力保障”转变为“安全兜底、调节支撑”，深度调峰运行将常态化。现有研究表明，机组低负荷运行下PSS 原整定参数仍具备较好的涉网性能［8，21］，但近期中国内蒙古某660 MW 火电机组在深度调峰的进相工况发生了功率振荡，振荡频率为1.8 Hz，最终确定是由于PSS 内部转速测量误差过大引起PSS 提供负阻尼作用。通过开展深度调峰工况下PSS 阻尼特性分析及现场试验，可有效验证和优化其涉网性能，保障机组和电网的安全稳定。

本文结合上述振荡事件分析PSS 在深调进相工况下提供负阻尼的原因，并开展加速功率型PSS转速计算电抗参数适应性机理分析，通过实验室励磁装置数字物理混合仿真测试和现场试验验证，对PSS 转速计算用电抗参数的取值提出了整定建议。

1 加速型PSS 原理

1.1 不同工况下加速型PSS 作用机理

典型加速功率型PSS 的传递函数如图1 所示。图中，Δω和ΔPe分别为转速变化量和电功率变化量；TW1至TW4为隔直环节时间常数；T1至T4、T10、T11为超前滞后环节时间常数；T7为电功率计算时间常数；T8和T9为陷波器函数G（s）的时间常数，主要用于过滤轴系扭振和噪声信号；M、N为陷波器函数系数；KS1至KS3分别为PSS 增益、电功率计算补偿因子和功率匹配系数；ΔPa为加速度功率变化量；ΔPm为合成机械功率的偏差；USmax和USmin分别为PSS 的输出上限、下限值；ΔUPSS为PSS 的输出值；TP1 至TP7 为某励磁厂家装置程序中PSS 内部观测位置，对应的输出内部变量分别为TP1至TP7。由图1 可见，ΔPa由合成机械功率的偏差乘以陷波器函数后，再减去电功率的变化量得到［7，14］：

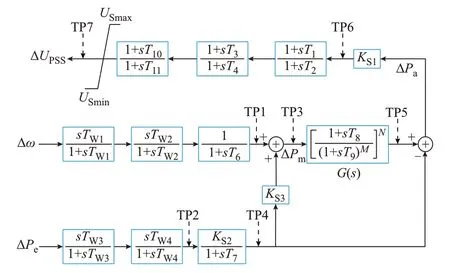
图1 加速功率型PSS 传递函数图Fig.1 Transfer function diagram of power-type PSS with improved rotational speed

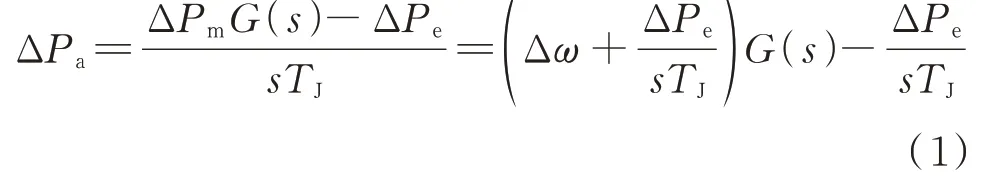
式中：TJ为机组总转动惯量。

若发电机有功功率变化由系统侧振荡引起，Δω和ΔPe经隔直和积分环节后的数值相等、极性相反，二者合成后输出信号ΔPm为零，此时加速度功率变化量ΔPa为负电功率偏差信号的积分，经增益、超前滞后等环节后可有效抑制电网有功功率的波动，提供正阻尼作用，有

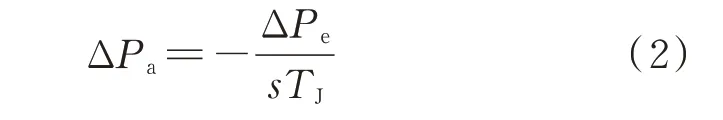
若发电机有功功率变化由调节原动机机械功率改变引起，ΔPe会发生较大变化，但Δω变化较小，二者合成后输出信号ΔPm将不为零，此信号将通过陷波器并与电功率偏差量信号相减。由于陷波器在反调频率范围内的增益近似等于1，因此二者相减后形成加速功率变化量信号ΔPa很小，PSS 输出近似为零。有

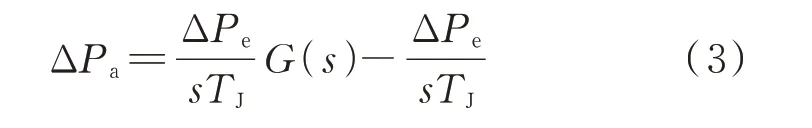
加速功率型PSS 正是利用加速功率信号来平衡机械功率改变引起发电机有功功率变化时的输出，使PSS 仅在系统发生低频振荡时才起作用。

1.2 转速计算方法

实际励磁装置通过采集到的机端电压、电流以及电抗参数计算发电机q轴内电势Ėq，进而求取Ėq的角频率作为机组转速信号输入至图1 中Δω。发电机电动势、电压等相量关系如图2 所示，其中，odq为dq坐 标 系，oxy为 同 步 坐 标 系，V̇t为 发 电 机 相 电压，İt为发电机的相电流，Xq为交轴电抗。

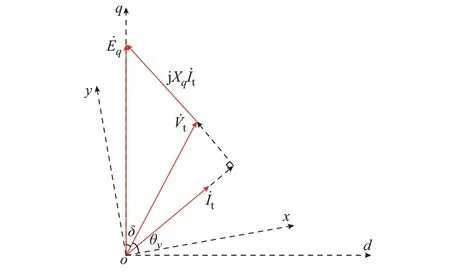
图2 发电机功角相量关系图Fig.2 Relation diagram of generator power angle and phasor

由图2 可以得出Ėq与x轴的夹角θq=δ+θv，通过对θq求导即可得到Ėq的角频率。其中，电压V̇t与x轴的夹角θv易通过对电压信号进行过零点检测得到，各励磁厂家装置相关处理基本一致，而如何在扰动过程中计算得到准确的发电机功角δ是PSS 转速获取的技术难点，也是影响PSS 阻尼特性的关键。发电机功角δ的计算方法如式（4）所示，通过对δ求导可获取δ的角速度ωδ，如式（5）所示。本文主要基于式（5）进行电抗参数、机组运行工况对转速计算影响的机理分析。

式中：P为有功功率；Q为无功功率；Ut为发电机机端电压；XPSS为励磁厂家整定的电抗参数，一般在Xq''与Xq之间，所有变量单位均为p.u.。

2 深调进相工况PSS 引发振荡事故分析

2.1 现场PSS 引发功率振荡事件概述

现场稳定运行的自并励发电机的额定功率为660 MW，振荡前初始运行工况：有功功率为99 MW（15%额定功率），无功功率为10 Mvar，准备进行深调工况下进相试验。当时PSS 为投入状态，已在75%额定功率下完成了PSS 相关试验，涉网性能满足标准要求。

进相试验过程中电厂运行人员进行减磁操作，在无功功率Q降至-170 Mvar 的过程中，机端电压Uab、有功功率P、励磁电压Uf等电气量逐渐发生振荡，有功功率波动约5 MW，励磁电压波动约25 V，振荡频率1.70 Hz，退出PSS 后振荡平息，录波图见附录A 图A1。

2.2 PSS 引发负阻尼原因分析

影响PSS 作用效果的主要因素包括信号测量环节、隔直环节、相位补偿环节、PSS 增益KS1、电功率计算补偿因子KS2等。通过在现场大负荷工况和深调进相工况下扫频试验以及励磁装置参数定值确认，排除了图1 中相关参数整定不合理的问题。结合振荡过程中励磁调节器PSS 内部变量输出，分析PSS 引起功率振荡的原因。图3 为振荡过程中PSS内部变量输出录波图，其中，纵坐标为PSS 内部各输出变量的幅值，单位为p.u.。

当电网发生功率振荡时，PSS 正确的动作逻辑是图3 中TP1和TP4大小相同、符号相反，使得TP3接近为0，经过高频滤波后变为TP5，只有-TP4进入PSS 超前滞后环节为系统提供正阻尼作用。但从图3 可知，TP1的振荡幅值约是TP4的5 倍，造成了TP3有输出，经过T8、T9环节后TP5滞后TP3近180°（T8=0.6 p.u.，T9=0.12 p.u.），这 就 导 致 了TP5与TP4几 乎同相位，且振荡幅值约是TP4的2 倍，使得进入PSS超前滞后环节的输入变量由正确的-TP4变成了TP4，最终导致PSS 产生反向作用。

图3 励磁调节器PSS 内部变量输出录波图Fig.3 Output oscillogram of internal variables of excitation regulator PSS

通过与电厂确认，本次振荡不是由原动机异常调节造成，有功功率测量正常且TP4通道参数整定正确，但TP1与TP4无法对消。因此，引起PSS 产生负阻尼的原因是TP1输出异常，即PSS 转速计算环节，造成转速变化量成倍放大。该励磁调节器PSS 内部计算转速电抗参数XPSS为1.5 p.u.，与其他现场相比该定值偏大，初步认为是该定值在深调进相工况下适应性不足造成了本次PSS 负阻尼作用，从而引发了功率振荡。

3 实验室仿真测试

在实验室环境下，利用实时数字仿真（RTDS）仿真系统搭建包含353 MV·A 自并励发电机、主变压器、输电线路等设备的一次仿真系统，针对两套型号不同的励磁调节器装置进行了数字物理混合仿真测试，均发现PSS 采用偏大的电抗参数进行转速电气计算，在深度调峰、进相工况下阻尼特性变差，甚至出现负阻尼情况。

在发电机有功功率为281 MW（0.94 p.u.）、无功功率为45 Mvar（0.13 p.u.）的工况下，励磁装置分别退出、投入PSS 后进行机端电压5%阶跃试验，有功功率录波图见附录A 图A2，其中黑色曲线对应PSS退出情况，红色曲线对应PSS 投入情况，PSS 在大负荷工况下有效抑制功率振荡，有功功率从振荡5次变为1 次。

在发电机有功功率为35 MW（0.10 p.u.）、无功功率为-112 Mvar（-0.32 p.u.）的工况下，励磁装置投入PSS 后的有功功率P和转速变化量的录波图如图4 所示，其中，蓝色曲线对应PSS 转速信号采用电气量计算方法，电抗参数为厂家默认值（Xq=2.19 p.u.），红色曲线对应PSS 转速信号采用直采方法，机组实际转速变化量经外接板卡以±10 V（±10 V 代表转速±10 r/min）信号从RTDS 送入励磁装置。

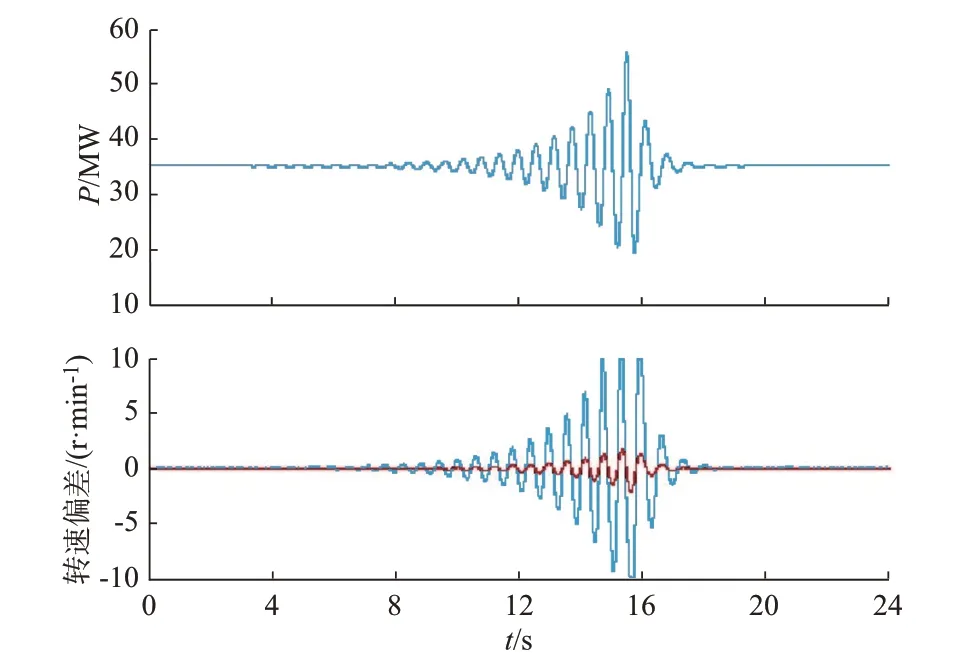
图4 有功功率和转速变化量录波图Fig.4 Oscillogram of active power and rotational speed variation

由图4 可见，采用电气量计算转速变化量与真实转速相位相同，但是幅值要放大数倍，与图3 中TP1效果类似，经过PSS 后续环节后造成了负阻尼作用，引发了功率的振荡，退出PSS 后振荡消失。通过仿真测试说明，PSS 采用偏大电抗参数，如Xq值，进行转速计算的准确性在大负荷工况下效果良好，但在深调进相工况下适应性变差。

4 PSS 转速计算电抗参数适应性机理分析

在相同电气量（如有功功率P）微小波动下，真实转速信号的变化量可以认为很小且固定唯一，而采用电气量计算方法得到的转速信号变化量则受到电抗参数取值以及机组运行工况的影响。

为了分析电气量微小波动在不同电抗参数或运行工况下对计算转速变化量的影响，基于式（5）求解转速对有功功率P和无功功率Q的导数，如式（6）所示。其求导结果的物理意义可以理解为在某个特定条件下，有功功率P或无功功率Q的微小波动对转速变化量的影响程度，求导结果的绝对值越大，代表转速变化量越大，反之转速变化量越小，但相同的功率波动下，真实转速的变化量是固定不变的。

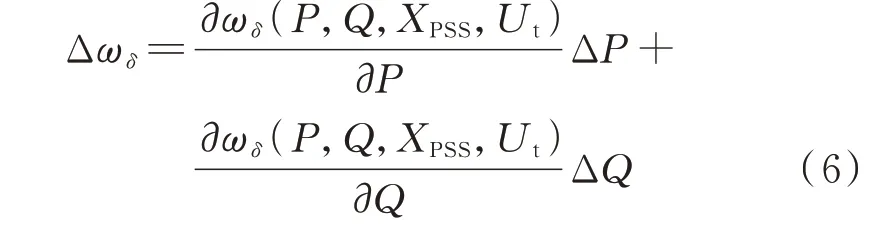
式中：Δωδ为转速变化量；ΔP为有功功率变化量；ΔQ为无功功率变化量。单位均为p.u.。

4.1 XPSS 不同取值对∂ωδ/∂P 计算结果的影响

首先，分析有功功率P的微小波动对转速变化量的影响，即式（6）中∂ωδ/∂P数值绝对值的大小。结合式（5），可以推导得到∂ωδ/∂P的计算公式为：

当机组参数Ut=1.0 p.u.，Q=-0.3 p.u.，XPSS分别为0.2、0.55、1.1、2.0 p.u.时，∂ωδ/∂P运算结果如图5 所示。

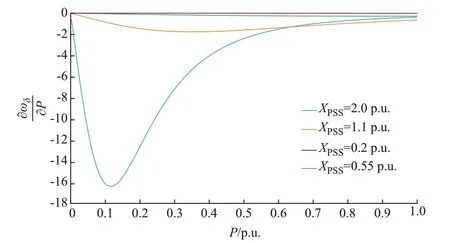
图5 XPSS取值不同时∂ωδ/∂P 的计算结果Fig.5 Calculation results of ∂ωδ/∂P with different XPSS

由图5可知，当机组在大负荷工况（0.6 p.u.＜P≤0.9 p.u.）且有功功率波动相同时，不同电抗参数对转速变化量的影响相差不大，且影响均较小；而当机组在小负荷工况（0.2 p.u.＜P≤0.6 p.u.）且有功功率波动相同时，不同电抗参数对转速变化量的影响相差很大，且电抗参数XPSS越大，∂ωδ/∂P的绝对值越大，即转速变化量的计算值也越大。

因此，如果电抗参数整定值偏大，则机组运行于深调、进相工况时，有功功率的波动会引起计算转速变化量与真实转速变化量的偏差增大，进而引起图1 中TP1输出一个比理论转速变化量更大的数值，造成TP3输出不为0，进而引起PSS 输出异常。

4.2 XPSS 不同取值对∂ωδ/∂Q 计算结果的影响

然后，分析无功功率Q的微小波动对转速变化量的影响，即式（6）中∂ωδ/∂Q数值绝对值的大小。结合式（5），可以推导得到∂ωδ/∂Q的计算公式为：

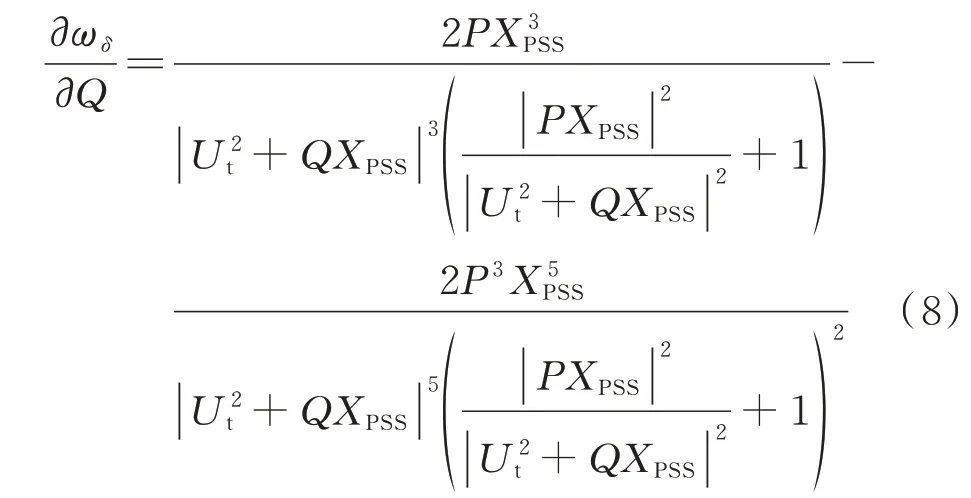
当机组参数Ut=1.0 p.u.，P=0.3 p.u.，XPSS分别为0.2、0.55、1.1、2.0 p.u.时，∂ωδ/∂Q运算结果如图6所示。

图6 XPSS取值不同时∂ωδ/∂Q 的运算结果Fig.6 Calculation results of ∂ωδ/∂Q with different XPSS

由图6 可知，机组深调工况下，当无功功率为迟相运行且无功功率波动相同时，不同电抗参数对转速变化量的影响相差不大且影响较小；而当无功功率为进相运行且无功功率波动相同时，不同电抗参数对转速变化量的影响相差很大，且电抗参数XPSS越大、机组进相越深，∂ωδ/∂Q的绝对值越大，即转速变化量的计算值也越大。

综上，采用电气量计算机组转速信号，相同波动下，转速变化量的准确度受电抗参数以及机组运行影响，即电抗参数整定值越大、机组有功功率越低、无功进相越深，转速变化量的计算值会越大，与真实转速变化量的偏差也就越大，甚至导致PSS 转速通道和电功率通道无法对消，引起PSS 阻尼特性变差。同时，当电抗参数XPSS向Xq接近（取值偏大）时，转速变化量随着机组有功降低、无功进相而变大，即相比真实转速的准确度变差，而当电抗参数XPSS向Xq''接近（取值偏小）时，转速计算准确度在机组全运行工况下均有良好的适应性。

5 现场PSS 验证与优化试验

针对本文所述660 MW 机组深调进相工况下PSS 引起功率振荡问题，通过理论分析与实验室仿真，发现了转速计算电抗参数整定值偏大后适应性不足的问题，在此基础上制订了现场PSS 验证与性能优化方案，并完成了相关试验。

5.1 不同电抗参数下的减磁进相试验

分别在电抗参数XPSS取1.5 p.u.、0.55 p.u.时投入PSS，在机组有功功率为99 MW、无功功率为10 Mvar 的初始工况下进行减磁试验。

1）XPSS=1.5 p.u.，进相深度至-170 Mvar，有功功率发生5 MW 左右的等幅振荡。

2）XPSS=0.55 p.u.，进相深度至-230 Mvar，有功功率未发生振荡。

在XPSS=1.5 p.u.下复现了本次功率振荡工况，PSS 内部TP1至TP6在振荡过程中的幅值、相位关系与图3 基本一致。而将XPSS整定为0.55 p.u.后减磁至-230 Mvar，有功功率仍平稳运行，满足进相试验要求的进相深度，解决了本次PSS 引发振荡的问题。

5.2 不同电抗参数下PSS 转速测量试验

为进一步验证XPSS取值对PSS 转速计算环节的影响，在发电机有功功率为99 MW、无功功率为-160 Mvar 的工况下将PSS 退出（转速测量误差不会引起功率的振荡），XPSS取值分别为0.2、0.55、1.1、2.0 p.u.时，对PSS 转速信号输出变量TP1进行了录波，不同XPSS取值下TP1的波动峰峰值以及PSS 稳态输出峰峰值如表1 所示。

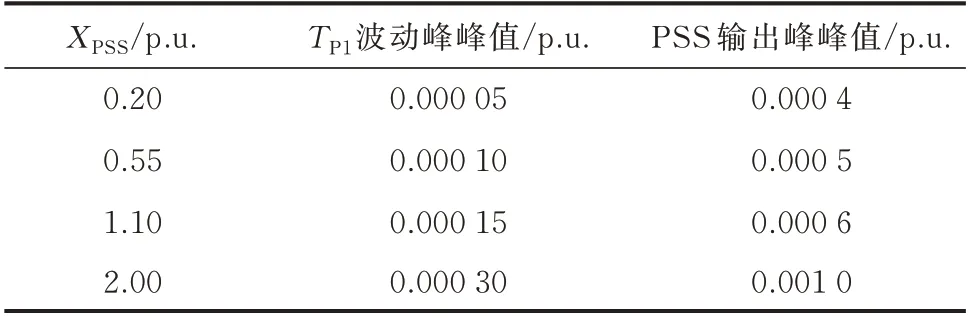
表1 不同XPSS下PSS 转速信号TP1测量波动值Table 1 Measured fluctuation value of PSS rotational speed signal TP1 with different XPSS

可以看出，电抗参数取值越大，机组深调进相工况下PSS 转速变化量测量值（与真实转速变化量误差）越大，通过本文分析该波动值的相位在本机振荡频率下经过PSS 环节后产生负阻尼作用，会引起有功功率波动增加，进而继续放大PSS 转速测量误差，最终引起功率的振荡发散。

5.3 不同电抗参数下的机端电压扰动试验

分别在电抗参数XPSS取0.2、0.55、1.1 p.u.时投入PSS，在机组有功功率为130 MW、无功功率为-80 Mvar 运行工况下进行机端电压+2%阶跃试验。附录A 图A3 为XPSS=0.55 p.u.时的试验录波图。表2 为不同XPSS下有功功率振荡阻尼特性。

通过附录A 图A3 和表2 可以看出，将电抗参数整定优化为0.55 p.u.后，PSS 在深调进相工况下阻尼特性良好，有效抑制了功率振荡。而电抗参数整定为1.1 p.u.后，扰动下不但没有抑制有功的波动，还产生了弱负阻尼作用，振荡次数和阻尼比指标变差。

6 结语

本文针对加速功率型PSS 转速计算电抗参数适应性开展研究，分析了电抗参数整定值过大导致机组深调进相工况下PSS 引发负阻尼的原因。通过实验室励磁装置数字物理混合仿真测试和现场实际机组PSS 优化试验，验证了理论分析的正确性。

1）励磁装置转速计算电抗参数整定值偏大是文中660 MW 机组深调进相工况下PSS 引发功率振荡的原因，导致转速通道输出信号幅值放大，经PSS各环节后产生负阻尼作用，将该值优化为0.55 p.u.后，PSS 在全运行工况下适应性良好。

2）基于主流励磁厂家电气量计算转速方法开展机理分析时发现，转速计算准确度受电抗参数以及机组运行影响，当电抗参数整定值增大时，转速计算准确度随着机组有功降低、无功进相而变差，即在深调进相工况时适应性差，易引起PSS 阻尼特性改变，甚至呈负阻尼。

3）综合考虑主流励磁厂家电抗参数整定建议以及电网相关管理要求，结合本文理论分析以及试验验证，建议加速功率型PSS 转速计算电抗参数的经验 取 值 范 围 从 原 来 的 采 用［Xq''，Xq］改 为［Xq''，0.5Xq］，以提升PSS 在机组全运行工况尤其深度调峰下的涉网性能。

4）目前，现场进行PSS 参数整定试验要求有功功率≥60%额定功率，当电抗参数取值偏大时，在大负荷工况下不易暴露相关问题。因此，建议调试单位和励磁厂家在进行相关试验时，重点关注该参数定值，尤其对于参与深度调峰机组，建议在深调工况下增加验证性试验，必要时优化调整电抗参数，以提升PSS 全运行工况下的涉网性能。

除了采用电气量计算转速实现方法、机组运行工况外，接入系统的位置不同以及本机振荡频率不同等电网侧因素也会对转速计算的准确性产生影响。因此，如何结合系统侧特征提出更准确的电抗参数取值建议是未来需要进一步研究的方向。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。