基于新课程标准的高中数学新旧教材比较分析——以人教版“圆锥曲线的方程”章节为例

云南省昆明市第一中学西山学校 张迎春

2019 年版普通高中数学教材已在多个省份试行，教材是新课程实施的载体，教师必须掌握、用好新教材，才能有效地落实新课程目标。

为探讨该问题，本文以2007 年版的人教版普通高中课程标准实验教科书数学A 版（以下简称“旧教材”）和2019 年版的人教版普通高中教科书A 版（以下简称“新教材”）为研究对象，从开章引言、正文内容、例习题、章小结四方面对“圆锥曲线的方程”内容进行比较分析，为教师理解教材和进行教学提供参考。

一、结构编排比较

通过表1，对新、旧教材的结构内容进行比较。

表1 新、旧教材的结构对比

变化1：删去“曲线与方程”这一小节，将这部分内容融入椭圆、双曲线、抛物线的学习内容中。新教材在建立圆锥曲线的标准方程后，就方程建立过程讨论“曲线上的点的坐标都满足方程”“以方程的解为坐标的点都在曲线上”。这样处理，既不失科学性，又不会让学生感到过于抽象，可以使学生在潜移默化中体验曲线与方程之间的一一对应关系，进一步理解通过方程研究曲线性质的合理性，使理性思维得到培养。

变化2：删去“探究与发现为什么截口曲线是椭圆”“阅读与思考二、圆锥曲线的离心率与统一方程”，增加“文献阅读与数学写作、解析几何的形成与发展”。增加内容为加深学生对相关内容的认识、扩大学生的知识面、运用信息技术学习等提供资源和机会。

二、章节导入比较

旧教材的章节导入用两页的篇幅，内容包括引言、章节标题、目录、背景图（拱桥），圆锥被三种不同位置的平面所截图。新教材的开章仅用了一页篇幅，保留引言部分，背景图变为太阳系各行星运行图，将圆锥被三种不同位置的平面所截图融合成一张，删去了章节目录。

在引言部分，新教材继承了旧教材的做法，从用一个平面截圆锥面谈起，引导学生思考三种圆锥曲线名称的由来，介绍了人类研究圆锥曲线的历史，告知本章主要研究的对象和研究的方法、研究的过程以及研究过程中渗透的数学思想，介绍圆锥曲线在科研、生产生活中的广泛应用，这增强了教材的可读性和指导性。

新教材删去了目录，因为主要内容在书本目录中已体现，就不需要赘述了。删除目录、缩减篇幅、整合图形，在体现数学简洁美的同时降低学生的阅读量，展现圆锥曲线的动态变化过程，引发探索圆锥曲线的统一方程的思考。

三、正文内容的比较

（一）主体内容比较

1.节引言的差异

旧教材小节内容从探究、思考、信息技术操作等方面进入教学内容，而新教材每小节都有节引言部分，例如，“椭圆”一节，配有节引言：“椭圆是圆锥曲线的一种，具有丰富的几何性质，在科研、生产和人类生活中具有广泛的应用。那么，椭圆到底有怎样的几何特征？我们该如何利用这些特征建立椭圆的方程，从而为研究椭圆的几何性质奠定基础？”

可以看到新教材从节引言开始，从宏观上提出问题，给出研究目标，而旧教材中没有这样的介绍（见表2）。

表2 新、旧教材的引言对比

2.“观察”“思考”“探究”栏目的差异

在每一种圆锥曲线的研究中，新、旧教科书都通过“观察”“思考”“探究”等栏目，根据知识的发生发展需要，提出层层递进的问题，从而形成环环相扣的系列化教学活动。这些问题是学生在学习具体内容时普遍都会遇到的，教科书通过它们来引导学生的思考方向，为学生独立思考、自主探究构建平台。但新旧教材在设问的方式上还是有较大差异，例如，“椭圆的简单几何性质”这一节中，

通过对比，可以看到新教材加大用坐标法思想分析问题的力度。从简洁性考虑，旧教材直接呈现逻辑过程，这是一种思考的“结果”，而对“为什么这样思考”则需要学生自己去体会，但这对学生而言是比较困难的。新教材比旧教材特别强调了用坐标法分析问题的环节，以“先用几何眼光观察，再用坐标法解决”为指导，完善学习过程（见表3）。

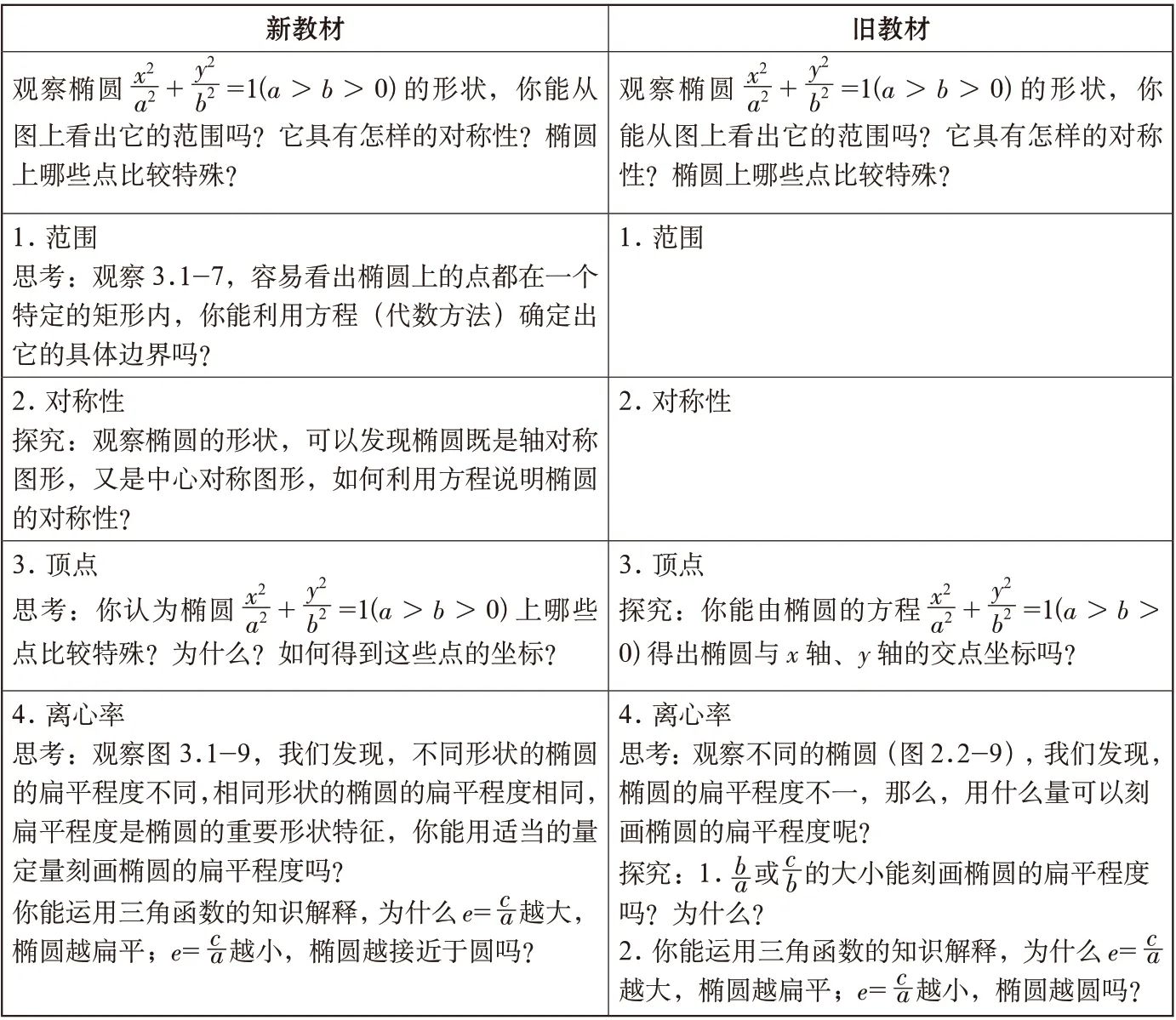
表3 新、旧教材“观察”“探究”“思考”设问对比

（二）信息技术应用、整合比较

《普通高中数学课程标准（2017年版）》要求重视信息技术的运用，实现信息技术与数学课程的深度融合。在旧教材中，双曲线的形成采用“拉链法”，学生对双曲线的形状感受不深，新教材则借助几何画板，通过对参数的控制使学生发现双曲线形成的条件，直观感受双曲线的形状，进而达到新课标的要求。

在“信息技术的应用”中，旧教材使用的工具是几何画板、图形计算器或其他数学软件，而新教材中则添加了Geogebra，并且在操作步骤上，新教材以Geogebra 为例，动态地展示了每一个操作步骤并配有截图。所以，相较于旧教材，新教材在对信息技术操作步骤的描述程度上显得更为细致。解析几何是数形结合的学科，“通过几何建立直观，通过代数予以表达”是其基本理念，新教材比旧教材更充分发挥信息技术的作用，为几何直观提供方便。

（三）数学文化融入比较

新课程标准强调将数学文化融入学习内容中。新旧教材的共性是通过例题、习题渗透圆锥曲线的数学文化、应用。例如，新教材“椭圆”一节的例5 通过电影放映机的原理介绍渗透圆锥曲线在实际生活中的应用；习题3.1 中的第7 题通过彗星“紫金山一号”的发现介绍，渗透圆锥曲线在天文研究中的应用等。同时，新教材沿用了旧教材通过设置“阅读与思考”栏目来展示数学文化材料的方式。如“圆锥曲线的光学性质及应用”详细介绍抛物线、椭圆、双曲线具有的光学性质以及光学性质在生活中的广泛应用。

另外，新教材增加了“文献阅读与数学写作”栏目。《普通高中数学课程标准（2017 年版）》特别指出：数学文化是指数学的思想、精神、语言、方法、观点，以及它们的形成和发展；还包括数学在人类生活、科学技术、社会发展中的贡献和意义，以及与数学相关的人文活动。解析几何是数学发展过程中的标志性成果，是微积分创立的基础。通过增加此栏目，将让学生系统了解解析几何产生和发展的过程、重要成果、主要人物，关键事件及其对人类文明的贡献，渗透数学文化。

（四）例、习题比较分析

通过表4 对新、旧教材的例、习题数量进行对比。

由表4 可知，总体数量上新、旧教材的例题数量相同，但练习题数量增加明显。认真研读新教材发现，新教材把每一种圆锥曲线的简单几何性质按照两课时进行，旧教材中习题分A 组和B 组两部分内容，但新教材分复习巩固、综合应用、拓广探索三个层次内容，拓广探索习题难度是最大的，这样的划分使习题层次性更加鲜明，更适合学有余力的学生。

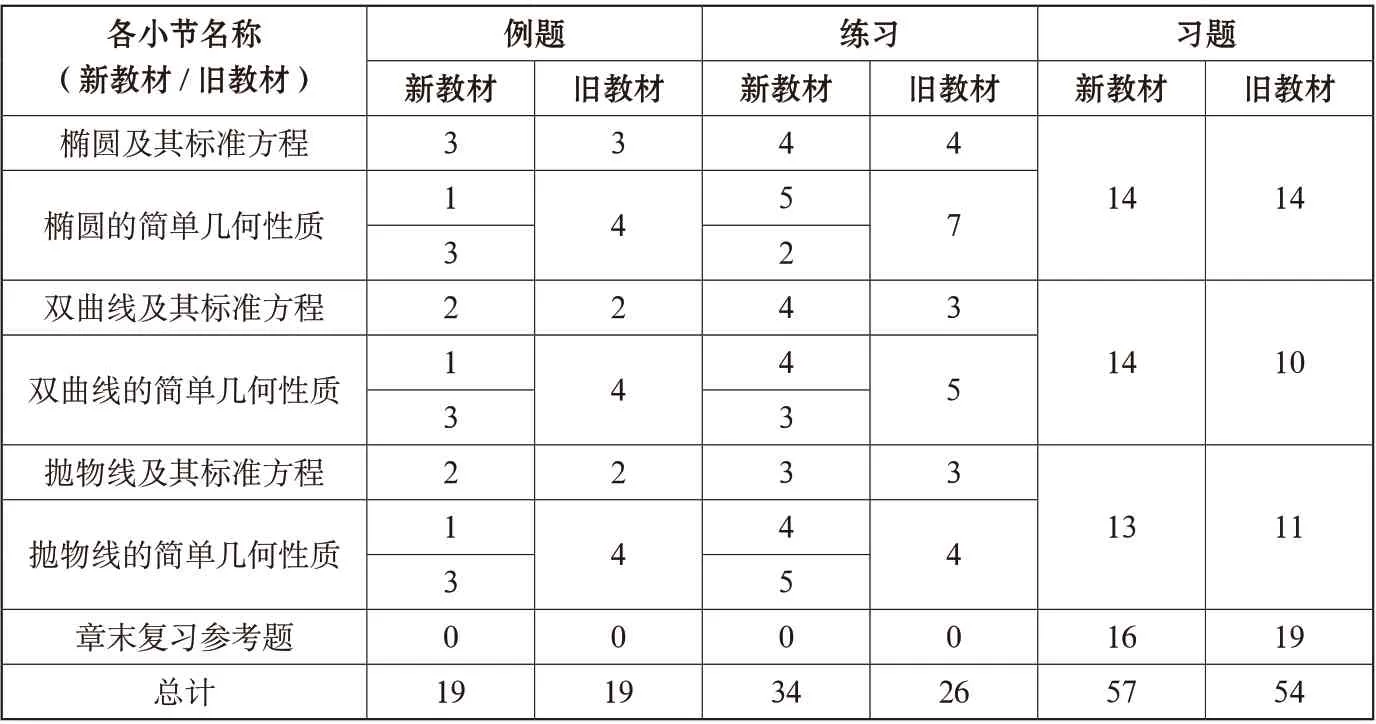
表4 新、旧教材的例、习题数量对比

新教材中练习题、习题总数量增加明显。《普通高中数学课程标准（2017年版）》中指出：“通过高中数学课程的学习，学生能进一步发展数学运算能力，有效借助运算方法解决实际问题。”解析几何的学习对运算能力的要求颇高，对学生而言，代数运算是高中数学学习的主要“拦路虎”，解题过程中，许多学生都是因为不能顺利完成代数运算而导致解答失败。练习、习题数量的增多，不仅能使学生更好地把握坐标法的基本思想，还能增加训练的机会，提升数学运算的核心素养。

四、小结比较分析

新、旧教材在小节上结构是一致的，主要包括“本章知识结构”和“回顾与思考”。

（一）知识结构比较

新教材的知识结构主要以知识框图的形式呈现，用流程图的形式串联本章知识要点、发展脉络和相互联系，从而形成思维导图。新教材的知识结构有机整合了各部分内容，并且在原有的基础上进行了扩展。总体而言，新教材的思维导图更加完整，知识点的呈现更加立体化。

（二）“回顾与思考”比较

新教材在回顾部分做了大的调整。新教材先对本章学习内容全面概述，接着用学习了的三种圆锥曲线，由特殊到一般总结曲线与方程的关系，将新教材删去的内容捡回。又结合本章的学习过程，总结用坐标法研究几何问题的具体方法，同时指出用坐标法研究几何图形时，代数式的化简、方程的变形与等价转化的重要作用，提出同学需关注逻辑推理、数学运算能力的提升，并强调研究圆锥曲线时，信息技术在发现问题、形成思想方法、获得结论等方面的重要作用。

可以看出旧教材的“回顾与思考”重视学习内容、学习过程的总结，新教材则更关心通过学习内容、学习过程对所反映的数学方法、数学思想、核心素养进行提炼与概括。

相较于旧教材用填表的方式对本章内容全面覆盖式的复习整理，新教材则以问题串的形式对本章学习内容进行整理。连续提出7 个问题，这7个问题系统、全面地驱动学生回忆和复习全章核心知识，通过在重点、难点和关键点上提出有思考力度的具体问题，深化学生对本章核心内容及其反映的数学思想和方法的理解，使学生在有所思的基础上还能有所悟。

总之，新教材更加充分地体现新课程标准的基本理念和目标要求，深入贯彻“立德树人”的教育理念，相较于旧教材，在结构、内容、习题、小结等方面均有较大改进。我们应关注到其中的变化，在继承旧教材的基础上把握好新教材，自然地完成从旧教材到新教材的过渡。