海上风机大直径单桩动态打桩过程数值仿真分析*
2022-11-27蔡舒鹏张永康霍小剑
蔡舒鹏,张永康※,金 晔,薛 驰,张 笛,霍小剑,林 峰
(1.广东工业大学机电工程学院,广州 510006;2.中铁建港航局集团有限公司,广东珠海 519075;3.江苏中天科技股份有限公司,江苏南通 226000;4.武汉理工大学,武汉 430070;5.武汉船用机械有限公司,武汉 430080)
0 引言
随着人类对能源资源需求的不断增长以及陆地资源的逐步紧缺,人类活动不断向海洋延伸,世界各国纷纷把海洋作为获取能源资源和发展经济的重要方向,通过海洋油气开发、海上风电开发、港口码头建设、跨海大桥建设等发展向海经济。我国海岸线长1.8万km,风能资源丰富,据估计近海可开发的风能约7.5亿kW,是陆地的2.96倍。“十四五”规划中,我国将海上风电作为解决能源危机、降低环境污染、实现“双碳目标”的国家战略。
近年来,随着国家“双碳目标”战略的不断推进,国内海上风电场的开发建设速度也明显加快,海上风电场的选址逐渐向离岸更远、水深更大的方向发展[1-5]。在海上风电场建设中,基础施工是项目建设中最重要的一个关键环节,单桩基础作为桩基形式的重要种类,在海上风机基础中占据相当比例。海上打桩作业一般由大型起重船或平台作为载体,利用其上的起重机通过液压锤吊打方式进行海上风电高桩承台桩和导管架桩等施工[6]。随着海上风电场离岸距离的不断提升,单桩基础中桩的尺度参数也在向着超长超大和超重方向发展,关于超大直径单桩贯入土体过程中海水的涌入及土的力学响应的研究还相对较少[7-10],因此研究超大直径单桩动态打桩过程中桩-土-水相互之间的耦合效应有非常重要的意义。
国外学者对桩-土之间的相互作用进行了广泛深入的研究,宋玉普等[11]考虑桩-土结构的耦合作用对导管架平台进行了优化设计,张兆德等[12]比较了ALE(Arbitrary Lagrangian Eulerian)和CEL(Coupled Eulerian Lagrangian)方法在计算岩土贯入问题时的优缺点,发现ALE算法相比CEL算法更能够保证土应力的稳定性,并能够保证材料-边界-网格的一致性运动,但在预测桩端极限承载力时结果偏大。王志强等[13]基于LSDYNA通过ALE算法对静压单桩沉桩过程进行了数值仿真,并讨论了桩头锥角、桩土摩擦因数和土壤分层对实心桩沉桩挤土效应的影响。王娜娜等[14]基于LS-DYNA通过ALE算法研究了小尺寸混凝土桩打桩动力下沉过程中土体的应力、变形和挤土效 应。Hamann等[15]基 于ABAQUS通 过CEL算 法研究 了土壤在部分排水的情况下的沉桩过程,并研究了渗透率对沉桩和周围土壤压力的影响。Wang等[16]研究了超大直径钢管桩在动态打桩的轴向力作用下面临的屈曲变形风险,发现控制椭圆度在30 mm以下对于减小钢管桩屈曲具有重要意义。
大尺寸单桩的动态打桩过程如图1所示。

图1 大尺寸单桩的动态打桩过程
本文旨在通过多物质ALE流固耦合方法对海上风机大直径单桩动态打桩过程进行数值仿真分析。以江苏启东H3海上风力发电场建设过程中的沉桩为工程背景,使用商用有限元软件LS-DYNA进行建模,对动态打桩过程中土体的应力、应变、体积分数以及沉桩阻力的变化规律进行仿真分析。为海上风机大直径单桩的动态打桩过程提供数值仿真建模参考和实用的分析方法。
1 多物质ALE流固耦合算法的原理
1976年,美国Lawrence Livermore国家实验室J O Hallquist博士主持开发完成DYNA程序系列,最初是作为军工上武器设计的分析工具。后来其版本和功能经过不断地更新和完善,使得DYNA程序的应用范围逐渐从军事推广到民用、商业等更多领域。在1988年,Hallquist创建了LSTC公司,将DYNA程序引入商业化发展轨道,并将之更名为LS-DYNA;1997年LSTC公司并与ANSYS公司合作,实现了LS-DYNA与ANSYS前后处理的连接,大大加强了LS-DYNA的前后处理能力和通用性,同时新开发了后处理程序LS-POST,极大地促进了LS-DYNA的发展。
LS-DYNA是非线性显示动力学的鼻祖和先驱,其具有Lagrange、Euler和ALE算法,Lagrange算法的单元网格附着在材料上,随着材料的流动而产生单元网格的变形。但是在结构变形过于巨大时,有可能使有限元网格造成严重畸变,引起数值计算的困难,甚至程序终止运算。ALE算法和Euler算法可以克服单元严重畸变引起的数值计算困难,并实现流体-固体耦合的动态分析。3种算法的主要特点如下。
ALE算法先执行一个或几个Lagrange时步计算,此时单元网格随材料流动而产生变形,然后执行ALE时步计算:(1)保持变形后的物体边界条件,对内部单元进行重分网格,网格的拓扑关系保持不变,称为Smooth Step;(2)将变形网格中的单元变量(密度、能量、应力张量等)和节点速度矢量输运到重分后的新网格中,称为Advection Step。
Euler算法则是材料在一个固定的网格中流动,在LS-DYNA中只要将有关实体单元标志Euler算法,并选择输运(Advection)算法。LS-DYNA还可将Euler网格与全Lagrange有限元网格方便地耦合,以处理流体与结构在各种复杂载荷条件下的相互作用问题。
为了说明问题,以一个2D的长方形变形为例来说明[17]。对于同一个物理过程,可以用不同的方式来描述:A Lagrangian,B Eulerian,C ALE,分别以上面3种方式来分别描述该物体的变形,分析其差别,如图2所示[17]。

图2 Lagrangian、Eulerian和ALE算法描述同一个物体变形时的区别
经过一个dt的时间变化后,比较3种描述的构形变化。
(1)A Lagrangian:对于拉格朗日描述,空间网格的节点与假想的材料点是一致的,也就是说,网格变形,材料也跟着网格变形,如图2中A所示,所以对于大变形情况,网格可能发生严重畸变。
(2)B Eulerian:对于欧拉描述,两层网格重叠在一起,一层空间网格固定在空间中不动,另一层附着在材料上随材料在固定的空间网格中流动,并通过下面两步来实现:首先,材料网格以一个拉格朗日步变形(像所描述的那样);然后拉格朗日单元的状态变量被映射或输送回到固定的空间网格中去。这样网格总是不动和不变形的,相当于材料在网格中流动,如图2中B所示,从而可以处理流体流动等大变形问题。
(3)C ALE:对于ALE(Arbitrary Lagrangian-Eulerian,任意拉格朗日-欧拉)描述,与欧拉描述一样,有两层网格重叠在一起,但空间网格可以在空间任意运动,其余与欧拉描述一样,有物质的输送在两层网格中发生。如图2中C所示,该方法可以整个物体有空间上的大位移,并且本身有大变形的非线性问题,如鸟撞飞机等问题。
海上风机基础施工时的动态打桩过程会使桩周围的土体产生大变形,若采用传统的Lagrange算法,就会导致在模拟计算过程网格严重畸变、求解时间步长不断减小,结果精度降低,甚至计算不收敛。因此,通过上述分析,可以采用ALE任意拉格朗日欧拉法将土体看成可流动的流体,而在空间上具有大位移的桩体为固体,土体网格的运动和桩体的运动分别独立描述,从而避免了土体网格产生严重的畸变。
2 有限元ALE流固耦合模型的建立
2.1 材料本构模型
2.1.1 土壤材料模型
LS-DYNA中提供的可以用来模拟土壤的材料模型有20多种,其中最常用的是5号材料模型,对应关键字*MAT_SOIL_AND_FOAM。该模型能通过合理的试验来确定其相关的材料参数,还能够可靠地预测土壤的弹性性能、体积压缩性能及其特殊的屈服特性,而且所需参数较少,在很多领域得到了广泛的应用,因此本文也采用该材料本构模型。
该材料模型遵循屈服面无应变强化的修正Mohr-Coulomb塑性模型,其非线性D-P屈服函数φ是静水压力的二次函数,表示为:

J2为应力偏张量不变量,可由下式计算得到:

而应力偏张量σ′ij与材料的静水压力有关,表示为:

其中静水压力σm可以通过3个方向的主应力计算得到:

具体的材料参数如表1和表2所示。
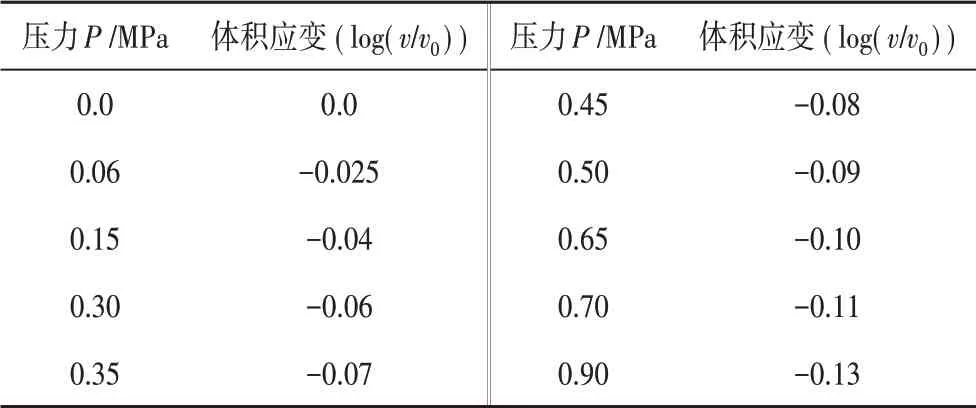
表1 土壤材料的压力-体积应变对应曲线值

表2 SOIL_AND_FOAM材料模型的参数及取值
2.1.2 桩体的材料模型
本文研究的桩体可以设置为线弹性材料或弹塑性材料,但因为主要研究对象是土体,而桩体的弹性模量比土体大得多,为了简化模型,减少计算时间,桩采用线弹性刚体模型,对应LS-DYNA中的20号材料模型,对应关键字*MAT_020_RIGID,详细的材料参数如表3所示。这里需要注意的是,根据实际工况,目前现场最大的打桩锤质量可达200 t,如果采用实心桩体建模,要控制其密度参数,使其质量达到约200 t,避免产生过大的惯性效应。

表3 桩体的材料模型参数
2.1.3 空物质材料模型
在桩体打入土体的过程中,由于占据了一部分土体的体积,土体上部靠近桩的部分会有隆起或下沉,引起“土拱效应”,为了让土体可以向上方流动,需要在土体上方预先定义一定厚度的空物质层,该层包含的物质材料可以为水,也可以为空气,其强度和刚度都为0,以此来容纳上部土体的变形,因为本文研究的是海上的打桩过程,所以空物质材料选取水及对应的状态方程。空物质材料在LS-DYNA中使用关键字*MAT_NULL定义,密度为1 000 kg/m3,状态方程使用关键字*EOS_LINEAR_POLYNOMIAL定义,具体参数如表4所示。
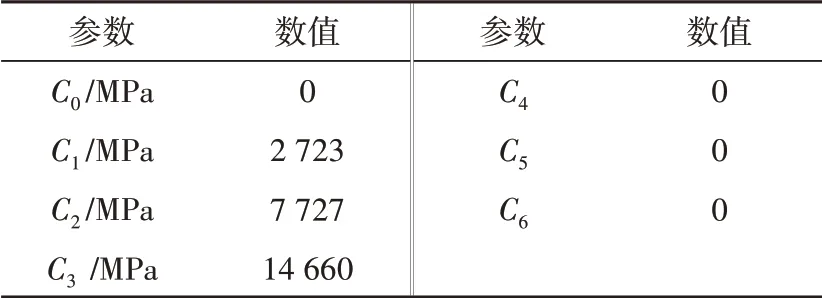
表4 空物质材料水的状态方程参数
2.2 边界条件及ALE流固耦合定义
本文建立的有限元模型如图3所示,其中桩体为圆柱实体模型,单元类型为SOLID164,而土和空气单元类型也均为SOLID164。桩体的半径为3 m,桩长度为25 m;通常情况下研究打桩过程地基土体应该为半无限大体,但在有限元建模中显然不可按照实际情况建立,相关研究成果表明动态打桩对土体的水平影响范围一般在10倍桩径以内,因此土体的水平边界取30 m,竖向取桩长度的1.2倍,即30 m;同时在土体上方定义了厚度为5 m的空物质层,意味着水深为5 m,同时让土体可以向上方流动。以桩底端为坐标原点,桩受打击方向为Z轴负方向建立有限元模型,为减少单元和降低计算量,桩和土体均采用1/4模型,在对称边界上分别设置对称边界条件,即在X面上限制X向的平动、Y和Z向的转动,在Y面上限制Y向的平动、X和Z向的转动;在土体外侧使用关键字*NON-REFLECTING_BOUNDARY定义非反射边界条件,这样由桩产生的应力波在到达土体边界时不会被反射,以达到半无限大体的效果。
在ALE流固耦合仿真中还需要通过关键字*ALE_MULTI_MATERIAL_GROUP定义多物质材料组分,这样在计算中界面重构时这两种组分可以互相混合。在本分析中,可流动的组分为土壤和水。在ALE流固耦合仿真中没有摩擦和接触部分的定义,但与之对应的是关键字*CONSTRAINED_LAGRANGE_IN_SOLID,其中SLAVE ID为拉格朗日描述的实体,即为桩,而MASTER ID则为ALE描述的实体,即为土壤和水,通过该关键字的定义,可以建立流体和结构之间相互作用的耦合机制。
建立好的模型单元总数为55 500个,节点总数为61 422个,桩与土壤接触部分采用细化网格,其余部分采用均匀划分的网格,如图3的缩略图所示。其中绿色实体为桩体,蓝色实体为空物质层(水层),红色部分为土壤。

图3 1/4桩-土有限元模型及桩头处的网格划分示意图
3 大直径单桩动态打桩过程数值仿真
大直径单桩动态打桩过程采用LS-DYNA进行显式动力学分析,其中土壤的自重采用动态松弛方法施加,对土壤施加恒定的Z向重力加速度-9.8 m/s2,对应关键字为*LOAD_BODY_Z,并使用关键字*CONTROL_DYNAMIC_RELAXATION使重力载荷以动态松弛的方法施加;然后使用关键字*DEFINE_CURVE在桩顶施加三角波压力载荷,最大锤击力为2 000 kN,因为本文主要研究动态打桩过程中的桩-土相互作用,所以这里采用了简化模型,没有考虑液压打桩锤的冲击载荷作用在桩体时的能量和应力波的传递,而是将冲击载荷直接作用在桩体上部,桩顶压力载荷-时间曲线如图4所示。
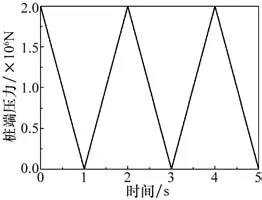
图4 桩顶压力载荷-时间曲线
3.1 土体应力场分析
大直径单桩动态打桩过程中桩贯入不同深度时土体的径向应力场(x向)分布如图5所示。可以看到在桩端附近的土体有明显的应力集中区,应力分量的等值线具有类似于“应力泡”的层状结构,这表明桩端土体具有类似球形的扩张形式。桩尖下的径向应力为压应力,其值随着贯入深度的增加而增大,“应力泡”的影响范围大致为5R,其中R为基桩半径。在桩尖下面6R时,径向应力迅速从高度压缩的状态减小到0。
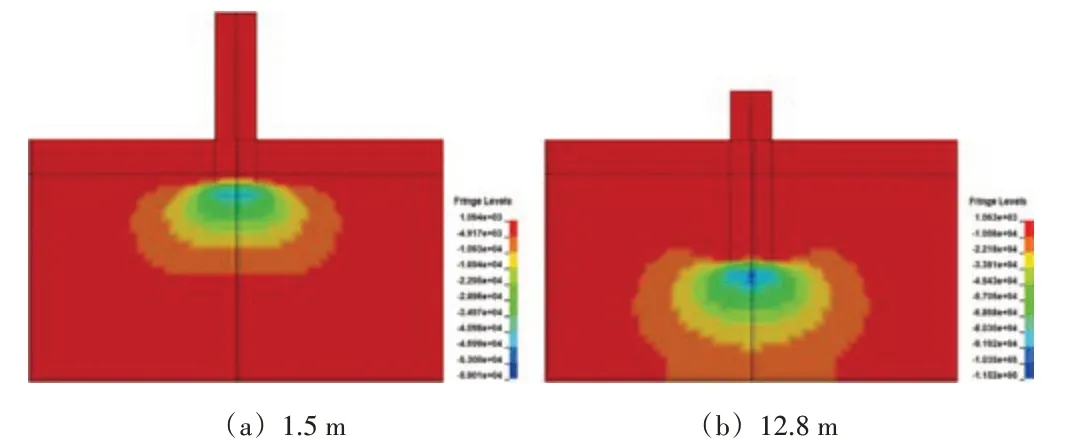
图5 单桩动态打桩过程中桩贯入不同深度时土体的径向应力场分布(单位:Pa)
大直径单桩动态打桩过程中桩贯入不同深度时土体的竖向应力场(z向)分布如图6所示。可以看到桩尖下的竖向应力也为压应力,其“应力泡”接近于椭圆形,相较于径向“应力泡”,其在径向的影响范围要小,大致为2.5R,但其竖直方向的影响范围更深,可达8R。
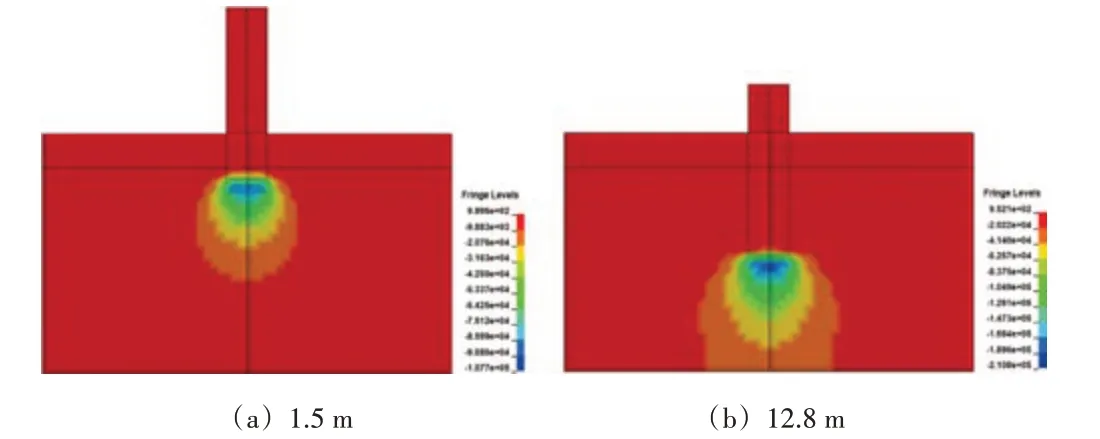
图6 单桩动态打桩过程中桩贯入不同深度时土体的竖向应力场分布(单位:Pa)
大直径单桩动态打桩过程中桩贯入不同深度时土体的切向应力场(xz向)分布如图7所示。可以看到桩端上下的应力符号相反,下端为拉应力,上端为压应力,整体呈“X”形状,并相较于桩尖附近,影响范围大致为8R。
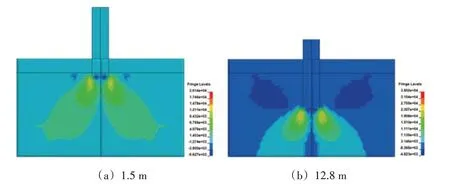
图7 单桩动态打桩过程中桩贯入不同深度时土体的切向应力场分布(单位:Pa)
大直径单桩动态打桩过程中桩贯入不同深度时土体的等效应力场分布如图8所示。可以看到等效应力在桩尖下部取得最大值,其“应力泡”形状接近于心形,水平影响范围为4R,竖直影响范围最大可达8R。
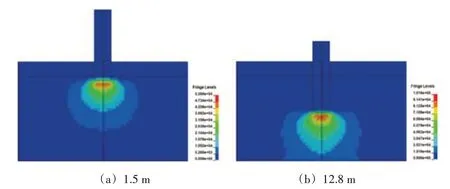
图8 单桩动态打桩过程中桩贯入不同深度时土体的等效应力场分布(单位:Pa)
横向比较不同贯入深度下的各应力等值线的数值变化,发现随着贯入深度的增加,桩尖处的压应力也在逐渐增大,但各应力集中区的影响范围和等值线的轮廓形状变化不大,说明动态打桩过程对土壤的影响范围是有限的。
3.2 土体应变场分析
大直径单桩动态打桩过程中桩贯入不同深度时土体的等效塑性应变场分布如图9所示。可以看到桩端附近的等效塑性应变大于桩侧的等效塑性应变,等效塑性应变在桩尖下部取得最大值,随着桩端的贯入,桩周围的土体逐渐受到压缩,在达到屈服应力后开始产生塑性应变并形成塑性变形区,形成了类似于“水滴状”的塑性变形区,随着贯入深度的增加,塑性变形区也逐渐增大,证明有更大范围的土体被扰动破坏,并发生了不同程度的塑性变形。

图9 单桩动态打桩过程中桩贯入不同深度时土体的等效塑性应变场分布
3.3 土体体积分数分析
桩土在ALE流固耦合分析时,欧拉网格节点和与材料节点是分离的,因此网格节点的位置变化并不能反映材料节点的位置变化,所以不能通过观察网格变形来得到物质的变形情况,但可以通过查看材料在网格中的体积分数的等值线来查看多物质材料的分界面情况,通过LS-PrePost后处理软件得到的大直径单桩动态打桩过程中桩贯入不同深度时土体的体积分数分布如图10所示。图中红色部分代表该区域土体的体积分数为1,而蓝色部分代表该区域水的体积分数为1。随着桩体的不断下沉,桩周的土体被不断挤开,并且桩周附近开始有水贯入,在水和土壤界面处土壤呈“开口状”,在距离桩身一定水平距离之外的土壤有微微隆起,这是受桩传递的应力冲击波所挤压的部分土体产生了位移。
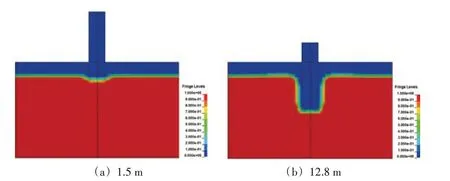
图10 单桩动态打桩过程中桩贯入不同深度时土体的体积分数分布
3.4 打桩阻力分析
桩-土之间的作用力可以通过二进制文件dbfsi输出,在k文件中通过设置关键字*DATABASE_FSI进行激活,图11所示为单桩动态打桩过程中桩-土之间的阻力变化。可见随着每次锤击的进行,桩贯入土体的深度增加,所受到的阻力也不断增加,但每次击打过后,由于应力波的反射作用和土体受压缩出现的塑性屈服,桩会出现一定的反向位移,即回弹,从而导致沉桩阻力减小。如在0~1 s内桩上端压力从最大值逐渐减小为零,桩体受到不断减小的动态压力和不断增大的阻力的共同作用,因此会先向下移动一段距离再向上回弹一段距离,直到第二个阶段1~2 s桩上端的压力又开始逐渐增大,使桩重新开始向下移动。
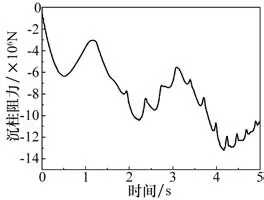
图11 单桩动态打桩过程中桩-土之间的阻力变化
需要注意的是,本文暂未考虑土的孔隙水压力对沉桩阻力造成的影响。在实际工程操作中,打桩过程中桩周土体会积累很大的超静孔隙水压力,使桩周一定范围内土体发生水力劈裂现象,导致桩周土体排水固结及强度恢复速度加快,停锤时间越长,土体强度恢复程度越大,造成后继打桩困难甚至拒锤现象的发生。
4 结束语
本文使用商用有限元软件LS-DYNA进行建模,通过多物质ALE流固耦合方法对海上风机大直径单桩动态打桩过程进行了数值仿真分析。研究了大直径单桩动态打桩过程中桩-土-水相互之间的耦合效应,得到了动态打桩过程中土体的应力、应变、体积分数以及沉桩阻力的变化规律,其结论如下。
(1)在桩端附近的土体有明显的应力集中区,应力分量的等值线具有类似于“应力泡”的层状结构,这表明桩端土体具有类似球形的扩张形式。发现随着贯入深度的增加,桩端处的压应力也在逐渐增大,但各应力集中区的影响范围和等值线的轮廓形状变化不大,说明动态打桩过程对土壤的影响范围是有限的。
(2)桩端附近的等效塑性应变大于桩侧的等效塑性应变,等效塑性应变在桩端下部取得最大值,随着桩端的贯入,桩周围的土体逐渐受到压缩,在达到屈服应力后开始产生塑性应变并形成塑性变形区,形成了类似于“水滴状”的塑性变形区,随着贯入深度的增加,塑性变形区也逐渐增大,证明有更大范围的土体被扰动破坏,并发生了不同程度的塑性变形。
(3)随着桩体的不断下沉,桩周的土体被不断挤开,并且桩周附近开始有水贯入,在水和土壤界面处土壤呈“开口状”,在距离桩身一定水平距离之外的土壤有微微隆起,这是受桩传递的应力冲击波所挤压的部分土体产生了位移。
(4)随着每次锤击的进行,桩贯入土体的深度增加,所受到的阻力也不断增加。但每次击打过后,由于应力波的反射作用和土体受压缩出现的塑性屈服,桩体会先向下移动一段距离再向上回弹一段距离,从而导致沉桩阻力先增大后减小,直到下一锤击又开始。
