基于光纤旋转连接器的光纤耦合效率研究
2022-11-26宋巍谢友金李治国郝伟闫佩佩李昕孙传东
宋巍,谢友金,李治国,郝伟,闫佩佩,李昕,孙传东
(1 中国科学院西安光学精密机械研究所,西安 710119)(2 中国科学院西安光学精密机械研究所中国科学院空间精密测量重点实验室,西安 710119)(3 中国科学院大学,北京 100049)
0 引言
光纤通信具有更高的带宽、大容量、结构简单、无需频谱许可和良好的保密性,被认为是工业领域、医疗设备等的关键技术,逐渐被广泛使用[1-5]。光纤旋转连接器是利用光纤通信技术实现静止平台和相对转动平台间信号传输功能的重要设备,其原理为从静止端(或旋转端)光纤发出的光束进入渐变折射率透镜(Gradient-index Lens,G-Lens)准直后成为空间准直光束,再传输至旋转端(或静止端)渐变折射率透镜,耦合至光纤中实现光信号传输。因此,光纤耦合效率是光纤旋转连接器的重要参数。
光纤耦合效率自光纤技术发展以来,被国内外多家高校、研究所以及企业广泛研究。PALAIS J C等[6-7]研究了基于渐变折射率透镜的单模和多模光纤耦合问题,分析了横向误差、纵向误差和角度误差引起的功率损耗。YUAN S等[8]利用高斯场分布推导出两个单模光纤(Single-mode Optical Fiber,SMF)准直器之间耦合损耗的一般公式,基于此公式推导了单模准直器高斯光斑尺寸失配引起的耦合损耗公式,分析了不同误差对渐变折射率准直器耦合效率的影响。王驰等[9-10]利用高斯光束复参数矩阵变换方法推导了渐变折射率透镜光学特征参数的数学表达式。CUSWORTH S D等[11]将用于渐变折射率透镜轴向和径向偏移损失的几何光学模型,推广到角度倾斜失准损失的情况下。梁骁等[12]在几何光学和高斯光束理论的基础上,运用矩阵光学与高斯光束耦合理论,分析了基于渐变折射率透镜准直器的插入损耗和回波损耗等特性,采用衰减基准测试方法对理论计算进行实验验证。千应庆等[13]建立了一种光纤准直器和耦合效率理论模型,对光纤旋转连接器耦合误差进行分析,得到了误差对光路传输损耗的影响规律。魏莉等提出了一种基于G-Lens的高速单通道单模光纤旋转连接器的结构,对光纤旋转连接器中光信号传输时的损耗进行分析研究,实验结果表明,单通道单模光纤旋转连接器在8000 r/min的高转速下工作,插入损耗为19.6 dB。
综上可知,对于渐变折射率透镜与光纤耦合分析较多,但对于存在误差情况下,相关提升耦合效率的方法研究较少。目前光纤旋转连接器耦合过程存在的间隙误差对插入损耗影响程度不清楚。同时,加工和装配过程中位置误差无法避免,利用结构微调较为复杂。光纤旋转连接器中光纤与透镜的间隙以及透镜间的位置关系极大地影响着性能指标。并且,随着光纤旋转连接器的广泛应用,对其低损耗、高可靠等性能提出了更高的要求,因此本文重点介绍基于单通道光纤旋转连接器的间隙误差和位置误差的补偿方法。本文以单通道单模光纤旋转连接器为研究对象,光纤旋转连接器利用两个G-Lens准直器实现旋转状态下的光信号传输,对单模光纤出射光束进行扩束准直,放宽了光学器件的加工和装配误差。本文理论分析了G-Lens和光纤存在的位置误差以及G-Lens准直器间的位置误差对耦合效率的影响,并完成相关实验验证;从方法上提出修正光纤与G-Lens位置误差的方法和基于楔形棱镜和平板玻璃的光束指向调整法。本文研究对于低损耗单通道单模光纤旋转连接器具有参考意义。
1 系统模型
本文研究的单通道单模光纤旋转连接器,是由两个G-Lens准直器组成的信号传输装置。该连接器已经广泛应用于工业控制、能源和医疗装备等领域[14]。其工作原理为,激光光束从单模光纤传输到G-Lens后准直光束,随后被准直的激光光束进入空气中传输,被相同参数的准直器接收后耦合至光纤中,如图1所示。在信号传输的过程中,其中一个由单模光纤和G-Lens组成的准直器沿着光轴旋转,这是与空间光-光纤耦合不同的地方。在这个耦合模型中,单模光纤纤芯与渐变折射率透镜之间的距离L1和L′1以及G-Lens1和G-Lens2相对位置关系是关注的重点。
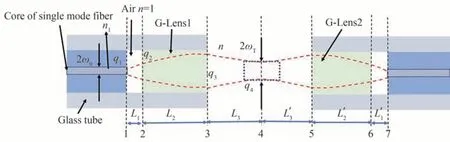
图1 高斯光束在两个G-Lens准直器间的耦合模型Fig.1 Coupling model of two G-lenses with Gaussian beam
1.1 渐变折射率透镜传输理论
本文采用径向分布渐变折射率透镜,其折射率分布沿着透镜径向呈抛物线型分布,其折射率分布表示为

式中,n0是G-Lens的中心折射率,g是渐变折射率梯度常数,r是到中心轴的距离。
通常,在准直器中G-Lens与单模光纤存在一定的空气间隙,如图1所示,从单模光纤输出的近似高斯光束束腰为ω0,通过空气(折射率n2=1),然后进入折射率分布由式(1)表示的G-Lens1,经过G-Lens1准直后进入有同样折射率分布的G-Lens2,耦合至单模光纤。经过G-Lens1准直的光束在距离透镜端面L3处,得到束腰为ωT的高斯光束。L1表示从单模光纤到G-Lens端面的距离,L2表示G-Lens的长度,L3表示G-Lens端面到束腰的距离。根据光学传输矩阵[15]可将高斯光束在间隙(面1到面2之间)的传输矩阵表示为

根据渐变折射率透镜的梯度常数g和透镜长度L2,将G-Lens传输矩阵表示为
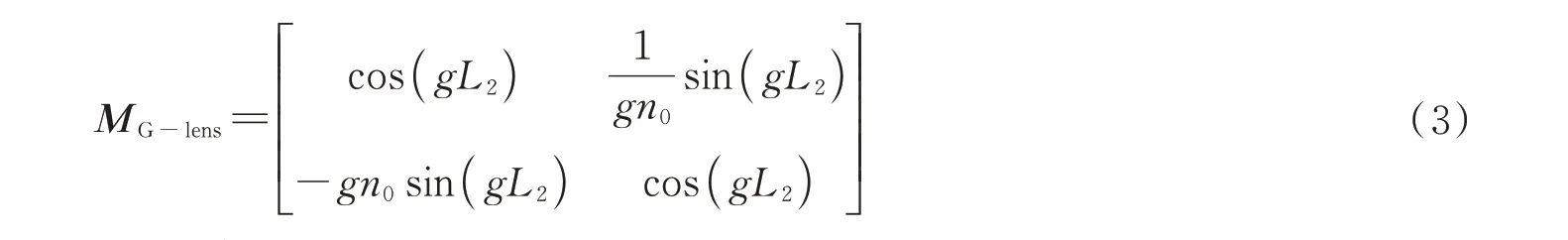
从光纤出射的光束经过G-Lens的传输矩阵M表示为
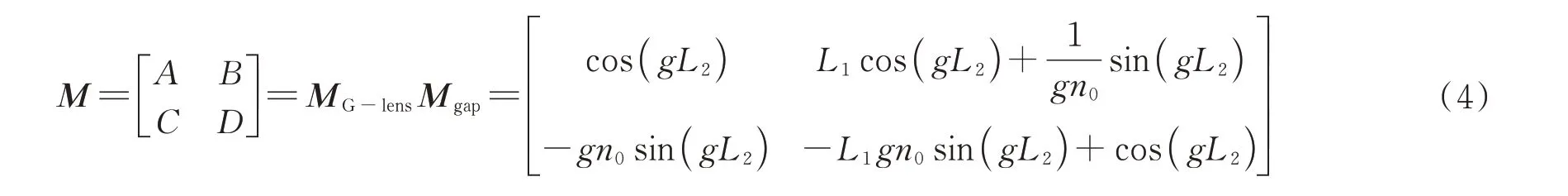
高斯光束参数q(z)表示为

式中,R(z)是高斯光束等相位面曲率半径,ω是束腰大小,λ是波长,n是介质的折射率。同时,利用ABCD矩阵法,可得面2处高斯光束参数q(2)的表达式为

根据入射面1的初始条件n=n2,ω=ω0,R(1)→∞,代入式(5)可得

在面4的高斯光束参数q(4)利用高斯光束参数q(z)的变化规律可得

由于面4处为束腰位置,等相面曲率半径为∞,结合高斯光束参数定义可知

变换可得

1.2 误差分析理论
本节理论分析了误差对光纤旋转连接器插入损耗的影响,这里所说的误差包含光纤与G-Lens透镜间的间隙误差、G-Lens透镜间的轴向、径向和角度三种误差。光线在存在一定误差情况下的传输过程及参数定义如图2所示。

图2 光纤旋转连接器存在误差情况下的传输过程Fig.2 Transmission with errors in fiber optic rotary joints
如图3所示,按照G-Lens透镜设计,高斯光束束腰在透镜出射端面上,为了更好地描述高斯光束在G-Lens中的传播,假定两个坐标系(x,y,z)和(x′,y′,z′),坐标原点均设置在光轴与G-Lens出射面交点处。

图3 高斯光束在G-Lens中传输路径Fig.3 Transmission path of Gaussian beam between G-Lenses
从单模光纤出射的光束经过G-Lens1准直后,高斯光束束腰位置在出射端面上,束腰大小为ω1,高斯光束电场复振幅的x方向分量可以表示为[16-17]

式中,E1是(x,y,z)在坐标(0,0,0)处的振幅,


在耦合损耗的分析中,由于损耗是两个G-Lens透镜失配引起的,有必要考虑接收端的复振幅。同理,可得接收端的高斯光束电场复振幅的x方向分量,可以表示为
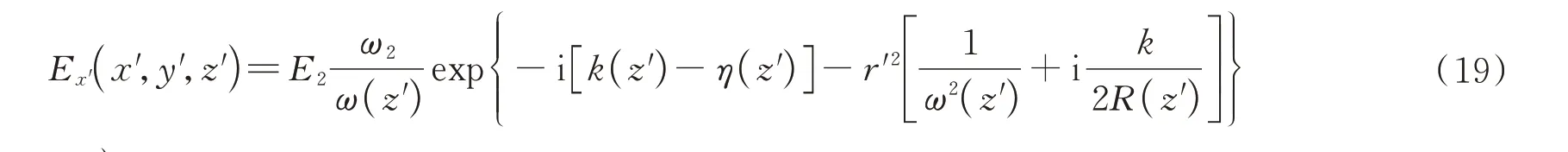
式中,E2是(x′,y′,z′)在坐标(0,0,0)处的振幅,且E1=E2,ω1和ω2是束腰半径(ω1=ω2),
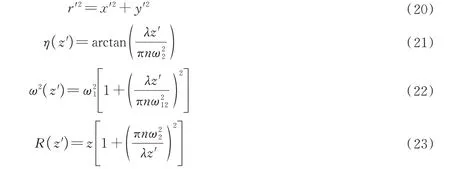
在G-Lens2端面进行光束耦合,耦合系数η表达式为[8]

根据图2,对(x,y,z)和(x′,y′,z′)这两个坐标变换,变换公式为

考虑传输中角度误差θ很小(一般θ<0.3°),可以认为cosθ≈1。将式(25)~(28)代入式(13)中,可得

对于接收端的高斯光束电场复振幅,当z′=0时,将式(20)~(23)代入(21)可得

由于系统的耦合效率T和插入损耗I可表示为

结合式(24)、(29)~(31)可得

如图4所示,对于轴向误差、径向误差和角度误差分别进行表示。根据式(32)和式(33)推导出这三种误差条件下引起的插入损耗。

图4 两个G-Lens轴向误差、径向误差、角度误差示意图Fig.4 Separation misalignment,lateral offsets,angular tilt misalignment between two GRIN lenses
当只存在轴向误差Z0时,角度误差θ和径向误差X0均为0值,其引起的插入损耗Ia可以表示为

当存在径向误差X0时,角度误差θ为0值,轴向误差仍为Z0,其引起的插入损耗Ib可以表示为

当存在角度误差θ时,径向误差X0为0值,径向误差仍为Z0,其引起的插入损耗Ic表示为

2 仿真分析
2.1 光纤与G-Lens位置误差
首先,将两个参数相同的G-Lens准直器对准,如图5所示,两个透镜间的间距为d,SMF-1和G-Lens1、SMF-2和G-Lens2之间的距离分别为d1、d2,G-Lens相关参数如表1所示。

图5 两个G-Lens准直器的光线追迹Fig.5 Ray tracing in two G-Lens collimators

表1 GRIN lens-1和GRIN lens-2的参数列表Table 1 Parameters of GRIN lens-1 and GRIN lens-2
由图5和表1可知,SMF-1、SMF-2与G-Lens的初始距离d1=d2=0.258 mm,两个准直器间的距离为5 mm,在不改变d的条件下,d1从0值以每次0.05 mm递增至0.45 mm,得到改变d1后的插入损耗变化值,如图6(a)所示,当d1在0.258 mm附近时,系统插入损耗较小,随着误差的增大(d1增大或减小),插入损耗逐渐增大。本文探究一种补偿d1误差的方法,根据理论分析可知,试图改变距离d2,达到减小系统插入损耗的效果。因此,在不同距离d1处,改变距离d2,得到不同位置处的插入损耗曲线,如图6(b)所示。由图6(b)可以看出,改变距离d2在一定程度上影响了系统的插入损耗。d1=d2=0.258 mm并不是系统插入损耗最小的唯一值,在不同距离d1条件下,会有一个距离d2与之匹配使得插入损耗减小至0.2 dB左右。为研究低插入损耗下距离d1、d2关系,给出d1+d2的曲线图以及d1+d2=0.43和d1+d2=0.53的直线图,得到图6(c)。由图6(c)分析可知,当d1与d2之和处于0.43~0.53之间时,可获得较低的插入损耗。因此,通过调节距离d2,可以弥补d1距离误差带来的影响。这为光纤与G-Lens存在位置误差提供了一种补偿方法,后续通过实验验证该方法的可行性。

图6 不同d1、d2位置处插入损耗曲线Fig.6 Insertion loss curves at different d1 and d2
2.2 G-Lens间误差分析及补偿方法
利用表1参数,对两个G-Lens准直器的轴向误差、径向误差和角度误差进行分析。如图4(a)和图5所示,在保证d1与d2不变的情况下,改变距离d,得到轴向误差对系统插入损耗的影响,如图7(a)所示。同样,如图4(b)所示,在保证距离d不变的条件下,改变两个G-Lens准直器之间的径向距离X0,得到图7(b)所示的径向误差对插入损耗影响的曲线。如图4(c)所示,在保证距离d不变的条件下,改变两个G-Lens准直器光轴之间的角度关系θ,得到图7(c)所示的角度误差对插入损耗的影响。

图7 不同误差下插入损耗Fig.7 Insertion loss curves under different errors
从图7(a)可知,当轴向误差从0 mm增大至14 mm时,插入损耗增大量约为0.02 dB,由此可见轴向误差对插入损耗的影响较小。从图7(b)可知,当径向误差从0 mm增大至0.25 mm时,插入损耗增大量约为9 dB,径向误差对插入损耗的影响较大,这是由于在存在径向误差的条件下,出射端的G-Lens透镜的光束并没有完全进入接收端的G-Lens透镜。从图7(c)可知,当角度误差从0°变化至±0.2°时,插入损耗增大量约为6.5 dB,由此可见微小的角度变化对插入损耗的影响较大。因此,需要更加关注径向误差和角度误差对插入损耗的影响。
位置误差在加工、装调中是无法避免的,为了降低系统的插入损耗,本文提出了一种运用基于楔形棱镜和平板玻璃的光束指向法,对传输光线调整,使得更多的光束传输至接收光纤中,提升系统的耦合效率,如图8所示。
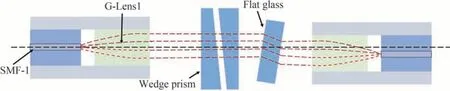
图8 光束指向法原理示意图Fig.8 Schematic of the principle of beam steering technology
光束指向法的原理为通过旋转两个楔形棱镜实现光束指向,让光束可以小角度偏转,再通过平板玻璃对光束传播的光轴微调,使得尽可能多的光束通过接收端的G-Lens耦合至单模光纤中。本文考虑同时存在径向误差X0和角度误差θ,仿真分析可得优化前后的插入损耗的变化曲线,如图9所示。当角度误差θ分别为0°和0.1°,工作距离为26.5 mm时,插入损耗随着径向误差X0的增大逐渐增大,通过本文所述的光束指向法调节后,可以使插入损耗稳定在0.7 dB左右,说明了该种方法有效,可以很好解决位置误差对插入损耗的影响。需要说明的是,本文中运用到主要光学元件如表2所示。

图9 优化前后插入损耗变化Fig.9 Insertion loss change diagram after optimization

表2 光束指向法中主要光学元件Table 2 Main optical components in beam steering technology
引入多个光学调整元件表面会引入附加的反射导致插入损耗增大,如图9所示,优化后的插入损耗为0.7 dB,小于无任何位置误差时的插入损耗值0.32 dB。这是因为无任何误差下的系统不添加多个光学调整元器件,但这种情况是非常理想的。当只存在角度误差0.1°时,不添加光学调整元器件的系统插入损耗为1.84 dB,大于优化后的插入损耗。总体来看,引入楔形棱镜和平板玻璃后的优化对于存在位置误差条件下的插入损耗具有明显提升,并且插入损耗0.7 dB满足系统的性能指标。
3 实验
实验步骤示意图如10(a)所示,LS是激光光源,FAS是高精度光纤对准台,I/R是插损回损仪,BM是双目显微镜。将单模光纤和G-Lens放置在高精度光纤对准台上,按照表1中的参数调整光纤和G-Lens透镜位置,调节至最佳耦合位置时,测量波长为1550 nm时的插入损耗,此时可认为是实验的初始状态。由于光纤与透镜没有固定,实验中高精度光纤对准台调节光纤与透镜距离时需要双目显微镜观察光纤移动。

图10 实验方案Fig.10 Experiment scheme
其次,移动单模光纤SMF-1与G-Lens1透镜端面贴合,通过高精度光纤对准台改变SMF-1与G-Lens1之间的距离d1,距离d1从0值以每次0.05 mm递增直到0.45 mm为止,保持距离d2不变,记录数据,与图6(a)中的数据对比得到图11,实测数据与仿真数据相差较小。在以上的基础上,当距离d1改变后改变距离d2,得到优化后的插入损耗值。本次实验选取了距离d1分别位于0、0.05 mm、0.10 mm、0.15 mm、0.20 mm、0.25 mm位置处,改变距离d2后观察插入损耗的变化值,即可得到不同距离d1,d2位置处的插入损耗值,与仿真数据相对比,整理数据后得到图12。

图11 插入损耗随距离d1变化实测与仿真对比Fig.11 Insertion loss of measurement and simulation with changing d1

图12 G-Lens1和G-Lens2在不同位置的插入损耗Fig.12 Insertion loss of G-Lens1 and G-Lens2 at different positions
最后,将光纤与G-Lens透镜之间的距离d1、d2通过高精度光纤对准台调整至初始状态(即d1=d2=0.258 mm),两个G-Lens透镜之间距离d为5 mm,在此初始状态基础上完成轴向误差和径向误差下的插入损耗实验。根据第二节的要求,将径向误差X0从0 mm增大至0.25 mm,得到图13(a)。在工作距离d为5 mm的基础上,轴向误差从0 mm增加至14 mm,得到不同工作距离下的插入损耗值,与仿真数据对比,得到图13(b)。

图13 轴向误差和径向误差对插入损耗影响Fig.13 Insertion loss influenced by lateral offsets and separation misalignment
4 结论
本文构建了基于光纤旋转连接器的光束传输模型,分析了G-Lens和光纤存在的位置误差以及G-Lens准直器间的位置误差对耦合效率的影响,分析表明G-Lens和光纤存在的位置误差和G-Lens准直器间的角度误差、径向误差对插入损耗的影响较大。利用ZEMAX软件对存在不同误差时的光纤旋转连接器插入损耗进行了仿真分析,与实验数据进行对比,验证了分析的准确性。针对G-Lens和光纤存在的位置误差,提出了修正光纤与G-Lens位置误差的方法,当G-Lens和光纤间的距离与初始距离差值为0.25 mm时,可以通过这种方法改善系统插入损耗至0.3 dB以下。针对G-Lens准直器间的位置误差,提出了基于楔形棱镜和平板玻璃的光束指向调整法,当存在微小角度误差和径向误差时,通过楔形棱镜和平板玻璃改变光束位置,使得系统插入损耗降低。本文以存在角度误差θ=0.1°,径向误差X0范围为-0.25~0.25 mm,利用光束指向调整法可以使得系统插入损耗降低至0.7 dB左右,较好地弥补了位置误差对系统插入损耗的影响。
