色偶极子模型中深度虚康普顿散射过程研究
2022-11-26向文昌蔡燕兵周代翠
向文昌,蔡燕兵*,周代翠
(1.贵州财经大学 金融物理重点实验室,贵州 贵阳 550025;2.华中师范大学 粒子物理研究所,湖北 武汉 430079)
微扰量子色动力学预言,随着能量的增加或动量分数的减少,强子内的胶子密度快速增加,在小x区域(当能量足够高时)形成高胶子密度的饱和状态,即色玻璃凝聚态(color glass condensate,CGC)[1]。CGC 中的胶子饱和现象可用非线性的JIMWLK 演化方程[2-5]描述,但JIMWLK 演化方程是极其复杂的无穷阶级联方程,对其解析和数值求解均十分困难,因此很难直接用于描述具体的物理观测量。另一种能描述胶子饱和现象的是非线性演化BK(Balitsky-Kovchegov)方程[6-7],BK 方程为JIMWLK 方程的平均场近似。BK 方程的重要结果之一是散射振幅的几何标度,并由此验证了HERA能区电子质子深度非弹性散射(deep inelastic scattering,DIS)的实验数据[8],间接表明了胶子饱和物质的存在,从而有力地支持了CGC 理论。
近年来,随着实验精度的不断提高和测量能区的不断扩大,CGC 理论得以较快发展。一方面,通过各种高阶修正,发展了一系列改进的CGC 演化方程,例如考虑跑动耦合常数修正(夸克圈修正)的次领头阶演化方程[9-10],同时考虑夸克圈修正和胶子圈修正的完整次领头阶演化方程[11]。另一方面,CGC 理论被用于描述各种实验观测量,例如单举过程的质子结构函数[12-13]和强子的产生[14],遍举过程实光子[15-16]和矢量介子的产生[17-18]。这些研究不但发展和完善了CGC 理论,而且促进了相关实验的发展。美国在建的电子离子对撞机(electron ion collider,EIC),其重要目的之一就是寻找CGC 存在的证据;我国设计的极化电子离子对撞机(electron ion collider in China,EicC),旨在通过与EIC 相互补充,丰富对CGC 理论的研究。
在CGC的诸多研究领域中,遍举过程比单举过程更易于探测CGC 中出现的胶子饱和现象,因为单举过程的散射截面仅正比于胶子密度的一次方,而遍举过程的散射截面正比于胶子密度的二次方,即遍举过程对胶子饱和更敏感[19]。特别地,对遍举过程中的衍射矢量介子产生和深度虚康普顿散射(deeply virtual compton scattering,DVCS)的实光子产生进行了大量研究,这些研究提供了胶子饱和的重要信息。但衍射矢量介子产生过程中,无法通过量子色动力学(quantum chromo dynamics,QCD)精确计算矢量介子波函数,模型存在不确定性。在DVCS 过程中,光子的波函数是可以精确计算的,且不需要引入模型参数。在HERA 能区,H1 和ZEUS实验组已经积累了丰富的不同转移动量区域的DVCS 实验数据,这些数据为精确研究质子的内部结构提供了场所。特别地,通过Bethe-Heitler 过程的干涉项可以很好地探测DIS 过程的广义部分子分布函数。因此,DVCS 过程成了研究胶子饱和最为理想的探针之一[20]。
色偶极子模型能较好地描述DVCS 过程实光子的产生。FAVART等[16]在色偶极子框架下基于BGBK(Bartel-Gder-Biernat-Kowdski)饱和模型研究了DVCS 过程实光子的产生,通过修正偏度较好地描述了大的光子虚度区域的实验数据。MARQUET等[21]利用色偶极子模型中领头阶水平的唯象IIM(Iancu-Itakura-Munier)模型预测了HERA 能区DVCS 过程实光子的产生,由于当时HERA 能区实验测量精度并不高,因此MARQUET等[21]的模型参数只能粗略地取自矢量介子产生过程。KOWALSKI等[22]在IIM 模型基础上引入了碰撞参数依赖,得到了b-CGC 模型;REZAEIAN等[23]利用b-CGC 模型计算了DVCS 过程实光子的产生并与HERA 能区的最新实验数据进行了比较,发现在大的质子转移动量平方区域,不同的偶极子模型给出的结果不一致。这是由于这些模型并没有考虑高阶效应,计算精度尚不足以定量描述真实的物理过程。
为提高色偶极子模型的精度,更好地描述DVCS 过程,本文将高精度的共线改进偶极子散射振幅用于研究DVCS 过程实光子的产生,通过拟合HERA 能区的最新DVCS 实验数据,得到微分截面下的χ2/d.o.f=0.51 和总截面下的χ2/d.o.f=0.89,同时抽取了DVCS 过程的斜率,所得结果与实验一致,CGC 理论的有效性得到进一步支持。
1 色偶极子模型对DVCS 过程的描述
1.1 色偶极子模型中的DVCS 截面
DVCS 是电子-质子深度非弹性散射中十分重要的过程,在DVCS 过程中,电子辐射的虚光子与质子发生相互作用,生成实光子,即γ*p →γp。由色偶极子模型,虚光子与质子的相互作用通常被认为是虚光子涨落形成的一对由正、反夸克(qqˉ)组成的偶极子与质子发生相互作用[22]。在质子静止参考系下,偶极子的寿命远长于其与质子相互作用的时间,因此DVCS 过程可看成3个时间上连续的子过程,如图1 所示。其中,I 为入射虚光子涨落成由正、反夸克组成的偶极子;II 为偶极子与质子通过交换胶子发生相互作用;III 为相互作用后的正、反夸克对重新融合成末态的实光子;z和1 −z分别表示夸克和反夸克所携带的虚光子的纵向动量分数,r表示偶极子的横向大小,t表示质子转移动量的平方,b表示碰撞参数,其值为偶极子中心到质子中心的距离。
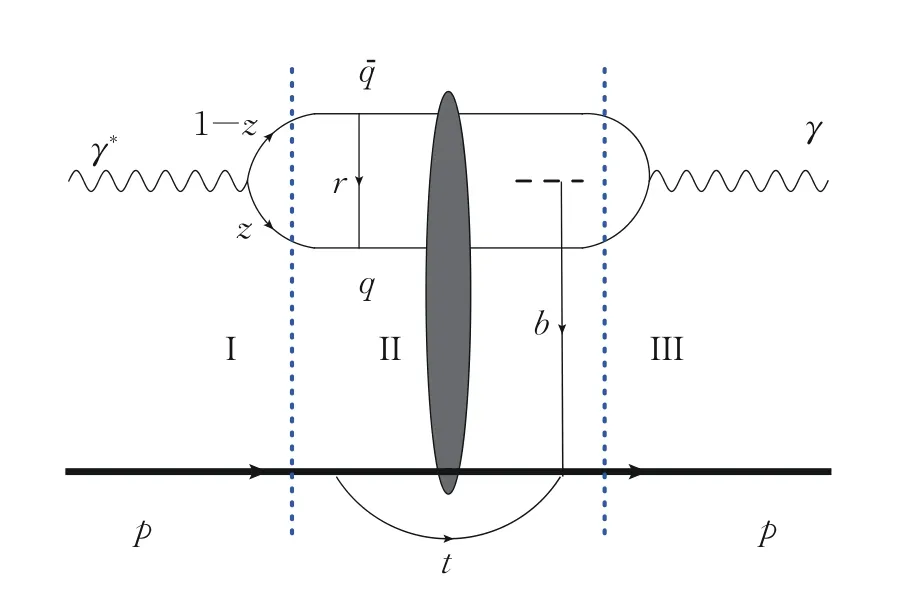
图1 色偶极子模型中DVCS 过程示意Fig.1 The DVCS diagram in the color dipole model
根据因子化理论,DVCS 过程的散射振幅可因子化为3个子过程所代表的物理量的乘积[22]:
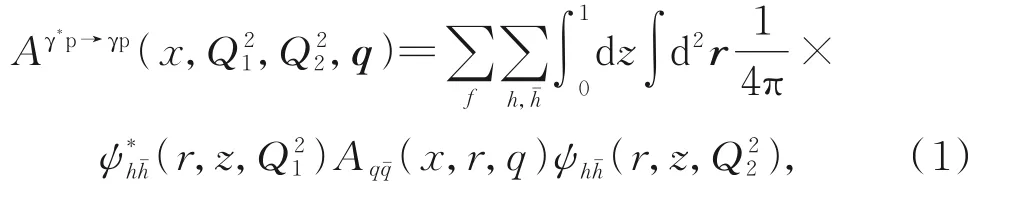

由光学定理,偶极子质子散射总截面可用偶极子向前散射振幅(t=−q2=0)的虚部表示,因此式(2)右侧b空间的散射振幅可进一步写为[22]

将式(2)和式(3)代入式(1),有
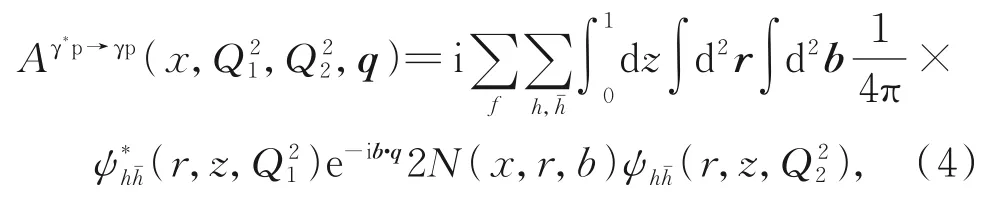
假定式(3)中的散射振幅只包含向前部分,考虑非向前部分的贡献需在仅考虑向前部分的式(4)中加入一个指数因子exp [±i(1 −z)rq/2]。式(4)中,N(x,r,b)为碰撞参数依赖的散射振幅,其变化满足偶极子演化方程,由于碰撞参数依赖的演化方程十分复杂,目前常用在IIM 模型中唯象地引入碰撞参数的依赖关系,因IIM 模型来自领头阶的BK 方程,所以引入的碰撞参数依赖的散射振幅本质上也是领头阶的。为提高DVCS 过程截面的计算精度,需将偶极子与质子的散射振幅推广至次领头阶水平,考虑碰撞参数依赖的散射振幅的复杂性,本文采用CEPILA等[24]的方法,将N(x,r,b) 因子化为三部分

其中,σ0为归一化常数,N(x,r)为偶极子散射振幅,r表示r的模,T(b)表示质子轮廓函数,碰撞参数的依赖由此函数体现。假定因子化后偶极子的散射振幅仅是偶极子横向大小的函数。将N(x,r,b)因子化的好处之一是可直接从偶极子演化方程中得到N(x,r),因此很容易推广至次领头阶水平。本文将采用高精度的次领头阶水平的共线改进的偶极子散射振幅;好处之二是分离的能量依赖(N(x,r))和碰撞参数依赖(T(b)),可在考虑高精度的偶极子散射振幅的同时考虑质子的量子效应。在DVCS 过程中,由于参与相互作用的质子能量非常高,质子的量子效应使其子结构在相互作用中出现波动。本文将质子看作由一系列高胶子密度区域组成的量子体,这些高胶子密度区域也称为热点。由于质子存在量子效应,热点位置将随相互作用事件的变化而变化。由CEPILA等[24]所用的模型,其质子轮廓函数为热点区域之和:

其中,Nhs表示质子中的热点数。每个热点均满足高斯分布:

其中bi表示质子中第i个热点的横向位置,bi的取值满足中心在原点(0,0)、宽度为Bp的二维高斯分布。因此参数2Bp表示质子横向半径平方的均值,同理,2Bhs表示热点半径平方的均值。
质子中的热点数Nhs是模型依赖的,在CEPILA等[24]的研究中,假设Nhs与能量相关,因此引入了动量分数依赖的热点数模型:

该模型在一定误差范围定量描述了J/ψ介子的产生,但并不完善。因Nhs为高胶子密度区域(热点)数,所以胶子密度仅是能量依赖的这并不合理。由QCD 实验和相关理论,胶子密度还应该是虚度(Q2)依赖的[25-26]。ZHANG等[18]受胶子密度公式启发,引入了Q2依赖的热点模型,很好地描述了J/ψ介子的产生。与已有模型相比,本文模型得到了较小的Bhs,间接揭示了热点半径随Q2的增大而减小,这与QCD 实验和相关理论相吻合,从而验证了本文模型的优越性。研究中,将Q2依赖的热点模型首次运用于DVCS 过程,引入Q2依赖后,热点数可参数化为[18]

其中,Λ=0.2 GeV;p0,p1,p2,p3为自由参数,经拟合实验数据得到。
由式(1)和式(4)知,要计算DVCS 过程的散射振幅,光子波函数是其中一个重要因素。与矢量介子波函数不同,光子波函数可由量子电动力学(QED)精确计算得到,因此在DVCS 过程中不存在波函数的不确定性,这使得DVCS 成了研究强子结构的最理想探针之一。由于DVCS 过程中末态光子为实光子,因此只有横向极化成分。简洁起见,定义光子重叠波函数为
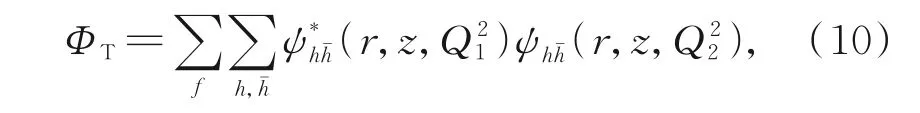
下标T 表示末态光子只有横向极化,极化求和后有[22]

由于末态光子为实光子,其虚度=0,因此=。式(11)中,Nc表示色数,αem表示电磁精细结构常数,mf和ef分别表示味为f的夸克的质量和电荷,K0和K1分别表示0 阶和1 阶二类修正贝塞尔函数。由式(10)及非向前部分贡献因子,DVCS 过程的散射振幅可写为

将式(6)和式(7)代入式(13),对变量b积分,将变量r化成极坐标形式,并对方位角积分,可得
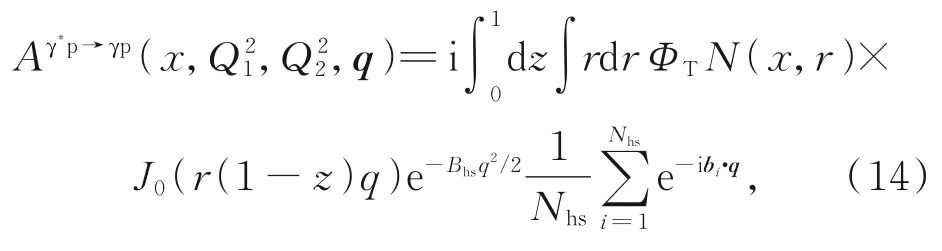
其中用了与式(5)相同的约定,q表示转移动量q的模,J0表示0 阶一类贝塞尔函数。由式(14),DVCS过程实光子产生的微分截面可写为[22]

对t积分,可得到DVCS 过程实光子产生的总截面。
1.2 偶极子散射振幅演化方程
计算微分截面的两个重要因素是光子重叠波函数和偶极子散射振幅,其中,光子重叠波函数可通过微扰QCD 精确计算,因此得到高精度微分截面的关键是提高偶极子散射振幅的精度。
自偶极子模型提出以来,如何获得能更好描述实验数据的偶极子散射振幅成为高能物理学研究的重点。按偶极子散射振幅的获得方法,大致可分为两类研究:一类是通过唯象模型得到偶极子散射振幅,模型参数通过拟合实验数据得到;另一类是通过计算不同精度的偶极子散射费曼图,得到相应的偶极子演化方程,通过解演化方程得到偶极子散射振幅。
第一类研究主要有GBW(Golec-Biernat-Wusthoff)模型[27]、BGBK模型[28]、IIM模型[29]。GBW 模型是在Mueller 偶极子模型框架下引入胶子饱和得到的,因此GBW 模型能很好地刻画胶子饱和这一物理性质,并且其散射振幅为偶极子横向尺寸r和胶子饱和动量Qs的函数(几何标度效应),这一效应在实验中得到了印证。但GBW 模型并不适合大转移动量区域,为解决此问题,BARTELS等[28]用 DGLAP(Dokshitzer-Gribov-Lipatov-Altarelli-Parisi)演化的胶子密度代替Qs,得到BGBK 模型。尽管此模型能很好地描述质子结构函数的实验数据,但并不适合在饱和区域进行DGLAP演化。基于此,IANCU等[29]通过解BK 方程得到了著名的IIM 模型。IIM 模型对HERA 能区的实验数据描述能力优于GBW 和BGBK 模型,但本质上IIM 模型源于BK 演化方程,因此其精度仍处于领头阶水平。
通过解演化方程得到的偶极子散射振幅,由于其是通过计算相应的费曼图得到的,因此容易扩展至包含高阶修正的情形。本文将采用由共线改进的偶极子演化方程计算DVCS 过程的偶极子散射振幅。为便于约定和引入相应的符号,先介绍领头阶的BK 方程。
BK 方程描述偶极子通过辐射软胶子随快度Y的演化,在大Nc极限下,其演化方程为[6⁃7]

其中,KLO为领头阶演化核,

其中,=αs Nc/π,αs为跑动耦合常数,r表示母偶极子的横向尺寸,r1和r2表示新产生的2个子偶极子的横向尺寸。
领头阶BK 方程仅对αsln(x)进行所有阶重求和,且αs为固定常数,因此方程的精度并不高。在用其描述HERA 能区质子结构函数时发现,理论值总比实验值大[12],原因是由领头阶BK 方程得到的偶极子散射振幅随快度快速演化,得到的偶极子散射振幅相对较大。为得到能更好描述实验数据的散射振幅,在BK 方程的基础上加入各种高阶修正,以压低散射振幅的演化速度,例如夸克圈(跑动耦合常数)修正[9-10]、胶子圈修正和非线性平方及立方胶子树图修正[11]。当用含夸克圈修正的偶极子散射振幅描述实验数据时,发现夸克圈修正过度会压低偶极子散射振幅随快度演化的速度[30],基于此,BALITSKY等[11]得到了一个完整的次领头阶BK演化方程(fNLOBK),但fNLOBK的数值解并不稳定,随着快度的增加,当偶极子的尺寸小于一定值时,其散射振幅会出现负值。LAPPI等[31]研究发现,其原因是方程中的双对数项产生了过大的辐射修正。
为解决fNLOBK的数值解不稳定问题,提出了两种处理方案:一是对演化核进行动力学限制,得到射弹快度Y表示下的非局域演化方程[32];二是对双对数修正进行到所有阶的重求和,得到Y表示下的共线改进演化方程[33]。此两方案等效,且均能使fNLOBK的解稳定。最新研究发现,偶极子演化方程最合适的演化变量不是射弹快度Y,而是靶快度η,因为实验中观测量通常是以η=ln(1/x)为自变量,并且在η下并不存在双对数项引起的不稳定性问题[34]。本文将采用η表示下的共线改进演化方程(BK-η)获得研究DVCS 过程中实光子产生的偶极子散射振幅。由于直接在靶快度下通过计算相应的费曼图得到相应的演化方程尚存在许多困难,因此采用DUCLOUE等[34]提出的变量变换方法,将Y表示下的BK 方程变换至η表示下。变量变换中Y和η的关系为

其中,ρ=分别表示入射偶极子和靶的特征横动量标度。由式(18),进行变量变换可将偶极子散射振幅变换至η表示下[34]:

式(20)和式(21)泰勒展开,并保留至一阶项,有
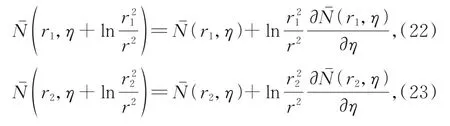
式(22)和式(23)中等号右边的第2 项为泰勒展开的一阶项,其中的偏微分部分满足偶极子演化方程,将领头阶的BK 方程代入式(22)和式(23),可得式(20)和式(21)的完整表达,将所得结果连同式(19)代入式(16),并加入胶子辐射应满足的时序条件,可得共线改进的偶极子演化方程BK-η[34]:

式(24)为靶快度η下共线改进的BK 方程。
2 数值结果
首先对BK-η演化方程进行数值求解,其次将得到的偶极子散射振幅用于拟合DVCS 过程的实验数据,由所得到的χ2/d.o.f,发现BK-η方程能很好地描述实验数据。
2.1 偶极子散射振幅的数值解
因BK-η演化方程(22)为复杂的微分积分方程,为得到偶极子散射振幅的数值解,用MV(McLerran-Venugopalan)模型作为方程演化的初始条件[35]
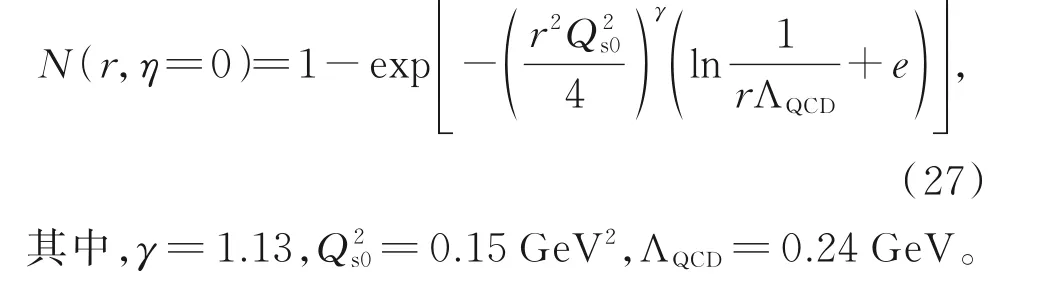
在数值计算中,将r和η均在二维网格离散化为256个点,对应于rmin=2.06×10−9GeV,rmax=54.6 GeV,ηmin=0,ηmax=20。用龙格库塔方法求解方程中的微分,用自适应辛普森方法求解方程中的积分,对不在网格内的点,用三次样条插值得到任意点的偶极子散射振幅。
2.2 DVCS 实验数据的描述
用数值形式的偶极子散射振幅拟合HERA 能区DVCS 过程实光子的微分散射截面和总截面的实验数据,拟合参数为式(9)中的自由参数p0,p1,p2,p3。共拟合了HERA 能区DVCS 过程中实光子产生的76个数据点,其中微分截面数据点28个,总截面数据点48个。
表1 给出了由共线改进演化方程(BK-η)得到的偶极子散射振幅拟合DVCS 过程实光子产生的拟合参数和相应的χ2/d.o.f。由表1的最后一列知,由共线改进的偶极子散射振幅得到的χ2/d.o.f较合理,表明由BK-η演化方程得到的偶极子散射振幅能很好地描述HERA 能区DVCS 过程实光子产生的微分散射截面和总截面的实验数据。

表1 DVCS 过程实光子产生的拟合参数和χ2/d.o.fTable1 The fitting parameters and χ2/d.o.f of the real photon production in DVCS
为更好地观察由BK-η演化方程得到的偶极子散射振幅对DVCS 过程实光子的描述能力,用表1得到的拟合参数,通过式(15)计算实光子产生的微分散射截面,并将其与实验数据进行比较。图2 给出了不同Q2和Wγ*p(光子质子质心系能量)下实光子的微分散射截面随|t|的分布情况。其中,(a)为ZEUS 实验组和当=82 GeV 时H1 实验组的结果,(b)为当Q2=10 GeV2时H1 实验组的结果。从图2 中可以看出,理论计算结果很好地描述了H1 和ZEUS的实验数据。

图2 不同Q2和Wγ*p 时DVCS 过程实光子产生的微分散射截面随|t|的分布情况Fig.2 The differential cross sections of the real photon pro⁃duction in DVCS as a function of |t|at different Q2 and Wγ∗p
为与实验数据所测范围保持一致,取t的积分范围为[0,1]。为进一步说明由BK-η演化方程得到的偶极子散射振幅能很好地描述不同类型的观测值,给出了实光子产生的总截面随Q2和的分布情况(图3)。从图3 中可以看出,除大Q2区域的少数点外,由BK-η得到的偶极子散射振幅均能很好地描述实验数据。在大Q2区域出现偏差的原因主要有两个:一是该区域的实验测量误差相对较大;二是当相同时,大Q2区域对应于大x,而CGC 理论主要适用于小x。
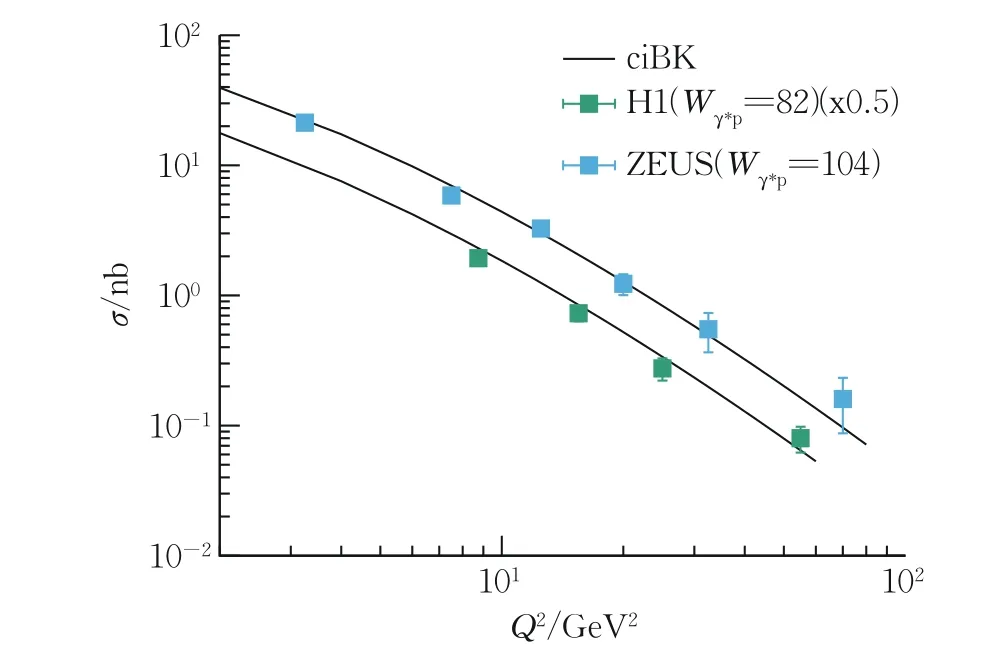
图3 DVCS 过程实光子产生的总截面随Q2的变化Fig.3 The total cross sections of the real photon production in DVCS as a function of Q2

图4 不同Q2 时DVCS 过程实光子产生的总截面随的变化Fig.4 The total cross sections of the real photon production in DVCS as a function of at different Q2
此外,为了从不同角度反映由BK-η演化方程得到的偶极子散射振幅能很好地描述DVCS 过程。基于dσ/d|t|∝e−bt抽取了DVCS 过程的斜率B,并与HERA 能区H1 实验组所测得的B进行了比较,见图5。斜率B为DVCS 过程的一个重要观测量,其值对应于质子中部分子的横向分布范围[38],因此B隐含小区域质子形状的重要信息[22]。由图5(a)知,随着Q2的增大,B呈缓慢减小趋势。从图5 中可以看出,在误差范围内理论抽取结果与实验测量结果一致。

图5 微分截面抽取的斜率BFig.5 The value of slope B extracted from differential cross sections
3 总结与讨论
基于色玻璃凝聚理论框架下的色偶极子模型,利用共线改进的偶极子演化方程研究了DVCS 过程实光子的产生。通过数值方法求解BK-η演化方程,得到了数值形式的高精度偶极子散射振幅。将该偶极子散射振幅用于拟合DVCS 过程产生的实光子的微分截面和总截面,得到了较合理的χ2/d.o.f。此外,基于理论计算的微分截面分布,抽取了相应的斜率B,所得结果与实验测量结果一致,表明由共线改进的演化方程计算得到的偶极子散射振幅能很好地描述HERA 能区DVCS 过程实光子产生的实验数据,研究结果进一步支持了CGC 理论的有效性。下一步拟将模型应用于更高精度的EIC 和EicC 能区,以进一步检测CGC 理论的优越性。
