张量积型Said-Ball 曲面的预处理渐近迭代逼近法
2022-11-26全浩荣刘成志李军成杨炼胡丽娟
全浩荣,刘成志,李军成,杨炼,胡丽娟
(湖南人文科技学院数学与金融学院,湖南娄底 417000)
在计算机辅助几何设计中,数据插值是一项重要的内容。传统的数据插值方法需要求解线性方程组,即配置方程。通常,线性方程组的系数矩阵是病态的,需研究高效的求解算法。为此,对配置方程的求解算法进行了研究并取得了不少成果,如基于Neville 消元的直接法[1-3]、基于矩阵分裂的迭代法[4-6]、子空间迭代法[7]等。近年来出现了一种具有几何意义的迭代算法——渐近迭代逼近(progressive iterative approximation,PIA)法。由于PIA 法具有稳定的收敛性、在迭代过程中易修改几何约束条件等优点而备受关注[8-9]。PIA 法最早源于齐东旭等[10]提出的盈亏修正思想。LIN等[11]证明了所有规范的全正基函数曲线(曲面)均具盈亏修正性质,并称之为PIA 性质。
虽然PIA 法已有许多成果,但由于其收敛速度慢,在相关应用领域难以发挥优势。近年来,PIA的加速方法研究逐渐成为几何计算中的热点。如加权PIA[12](weighted progressive iterative approximation,WPIA)法、带互异权值的PIA法[13-15]、Chebyshev 多项式加速迭代法[16]、带形状参数曲线的PIA法[17]等。由于PIA法等价于求解配置方程的Richardson 迭代法[6-7],文献[18]利用预处理技术对全正基函数的PIA 法进行预处理,得到收敛速度有明显提升的预处理PIA(preconditioned progressive iterative approximation,
PPIA)法。随后,文献[19]结合矩阵Kronecker 积的性质将预处理技术应用于张量积型Bézier曲面的PIA法。
预处理技术的引入虽然能通过改善配置矩阵的谱分布提高迭代法的收敛速度,但在迭代过程中需额外求解预处理子的逆矩阵,增加了计算量,影响数据插值的计算效率。为进一步降低预处理技术的计算量,文献[18-19]用经典的共轭梯度法近似求解预处理方程的法方程,即PPIA的非精确求解方法(inexact preconditioned progressive iterative approximation,IPPIA),但在求解过程中需在预处理方程两边同时乘以一个预处理矩阵的转置矩阵,显然,该法方程的条件数将随之增大,影响求解预处理方程算法的计算效率、计算精度和稳定性。如果能找到一种合适的算法直接求解预处理方程而不是其法方程,则可提升计算效率。但由于预处理方程的系数矩阵是非对称的,无法用共轭梯度法求解。文献[7]利用广义极小残差法(generalized minimal residual method,GMRES)求解配置方程,得到插值曲线,数值实例表明,当插值点较少时,GMRES 法的计算效率很高,但当插值点较多时,得到的插值曲线精度不理想[18]。欣慰的是,非精确求解方法对精度的要求并不高,因此,本文将利用GMRES 法求解预处理方程,以进一步提升算法的计算效率和计算精度。
基于上述分析,本文在文献[18-19]基础上,研究张量积型Said-Ball 曲面的PPIA 法及其非精确求解方法,以期进一步提高数据插值的计算效率。
1 相关工作
1.1 张量积型Said-Ball 曲面
Said-Ball 基函数及相应的张量积型Said-Ball曲面片的定义[20]为:

1.2 渐近迭代逼近法

则称S(0)(u,v)具有PIA 性质[11]。文献[11]证明了所有全正基函数曲线(曲面)均具PIA 性质。文献[20]称Said-Ball 基函数为全正基函数,从而张量积型Said-Ball 曲面也具有PIA 性质。

张量积型Said-Ball 曲面的PIA 性质意味着式(3)收敛于插值曲面S∗(u,v)的控制顶点,即

文献[6-7]指出,PIA 法中式(3)也可看作求解式(4)的Richardson 迭代法。
最后,给出矩阵的Kronecker 积的性质[21]。
引理1关于矩阵的Kronecker积,有:
(a)A⊗B可逆当且仅当A和B均可逆,且有(A⊗B)−1=A−1⊗B−1;
(b)若A,B,C和D为阶数满足AC和BD乘法的矩阵,则(A⊗B)(C⊗D)=(AC)⊗(BD)。
2 预处理渐近迭代逼近法
文献[18]利用对角补偿约化技术构造了预处理子,该预处理子能在很大程度上改善全正基函数(包括Bernstein 基函数和Said-Ball 基函数)所生成的配置矩阵的谱分布。文献[19]利用上述预处理子给出了张量积型Bézier 曲面的PPIA法,并取得了理想的加速效果。本文将该预处理技术应用于张量积型Said-Ball 曲面,得到张量积型Said-Ball 曲面的PPIA 法。
2.1 预处理子M1和M2的构造
首先,将配置矩阵B1分裂为


注1设M1和M2分别为对角补偿约化技术所定义的关于B1和B2的预处理矩阵,相应的半带宽分别为q1和q2,则有[18]:
(a)预处理子M1和M2均为可逆矩阵。
(b)对于i=1,2,经预处理后的矩阵的谱随半带宽qi的增大向1 附近聚集。
(c)综合考虑计算量和预处理效果,当预处理子的半带宽约为配置矩阵阶数的一半时效果较好。
2.2 预处理方法
在得到预处理子M1和M2后,由引理1,对式(4)进行预处理,有

注2文献[19]指出,在构造张量积型曲面的PPIA 法时,用矩阵的Kronecker积的性质分别对配置矩阵B1和B2进行预处理,具有充分发挥预处理子的预处理效果和提高算法的稳定性和鲁棒性的作用。
3 PPIA 法的非精确求解方法
由式(6),在PPIA 法的迭代过程中需计算

与式(3)相比,这显然增加了额外计算量。因矩阵的求逆运算计算量较大,且具有不稳定性。当n和m均较小时,式(7)很容易计算,但当n和m较大时,式(7)的计算复杂度增大,稳定性也随之降低,从而影响PPIA 法的计算效率。
注意到,计算式(7)等价于求解线性方程组

考虑用迭代法求解式(8),会得到一个嵌套迭代格式。将式(6)看作外迭代格式、将求解式(8)的迭代法看作内迭代格式,若对内迭代的精度要求较高,则求解式(8)需花费较多的计算时间。在不影响外迭代收敛性的前提下,降低内迭代的精度,可减少内迭代的计算时间,从而提高计算效率。因此,为减少计算量和提高算法的稳定性,考虑用GMRES 法求解式(8),得到的近似解。

其中,τk为给定的迭代终止误差阈值,‖⋅‖F为Frobenius 范数。
于是可得到下一步迭代的控制顶点
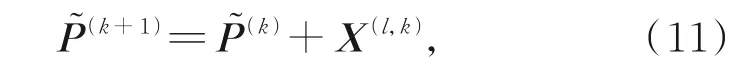
称式(11)为张量积型Said-Ball 曲面预处理渐近迭代逼近法的非精确公式,记为IPPIA-GMRES。
为提高计算效率,当
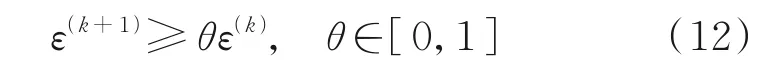
时,式(11)终止迭代,其中ε(k)为IPPIA-GMRES 法迭代k次所生成的近似插值Said-Ball 曲面的插值误差,

现讨论张量积型Said-Ball 曲面IPPIAGMRES 法的收敛性。为方便,下文的定理及证明中均将M1⊗M2记为M,将B1⊗B2记为B。
定理1设M1和M2分别为对角补偿约化技术所定义的关于B1和B2的预处理矩阵,P∗为Said-Ball 插值曲面的控制顶点。对于每个外迭代步k,利用GMRES 法求解式(9),得到式(7)的近似解X(l,k),则对IPPIA-GMRES 法迭代所生成的序列,有

定理1 得证。
由定理1,对于给定的预处理子M1和M2,IPPIA-GMRES 法的收敛性主要由τk决定。显然当τk=0时,利用GMRES 法可得到式(7)的精确解,此时IPPIA-GMRES 法退化为PPIA 法。因此,为使迭代法具有更好的收敛效果,τk越小越好。但τk越小,意味着对内迭代精度的要求增高,内迭代次数增加,计算量增大。在实际计算中,可在不影响外迭代收敛性的前提下降低对内迭代计算精度的要求(无需τk=0),以提高计算效率。
4 数值实例
文献[12]指出,在最优权系数下,WPIA 法比PIA 法具有更快的收敛速度,因此本文将与最优权系数下的WPIA 法进行对比。文献[7]利用GMRES 法求解曲线情形的配置方程,得到插值曲线,本文也将利用非重启的GMRES 法求解曲面情形的配置方程,得到插值曲面。由于GMRES 法的收敛性取决于系数矩阵的谱分布和Ritz 值等,而本文提出的预处理子能改善配置矩阵的谱分布,因此本文的预处理技术也可用于GMRES法,即预处理 GMRES(preconditioned GMRES,PGMRES)法。
方便起见,在数值实例中,记文献[19]的方法为IPPIA-CG。所有实验均在Intel(R)Core(TM)i7-8565U CPU @ 1.80 GHz 1.99 GHz、内存为8 GB的笔记本电脑上实现。
例1 给定16个待插值的数据点:(1,1,1),(2,1,2),(3,1,2),(4,1,1),(1,2,2),(2,2,2.5),(3,2,2.5),(4,2,2),(2,3,2),(1,3,2),(2,3,2.5),(4,3,2),(1,4,1),(2,4,2),(3,4,2),(4,4,1)。
例2 给定20个数据点:(1,1,1),(1,2,4),(1,3,2),(1,4,2),(1,5,2),(2,1,2),(2,2,2),(2,3,3),(2,4,6),(2,5,4),(3,1,3),(3,2,2),(3,3,4),(3,4,4),(3,5,3),(4,1,4),(4,2,6),(4,3,1),(4,4,1),(4,5,2)。
例3 逼近从函数

上采样得到11×12个数据点:

例4逼近从函数
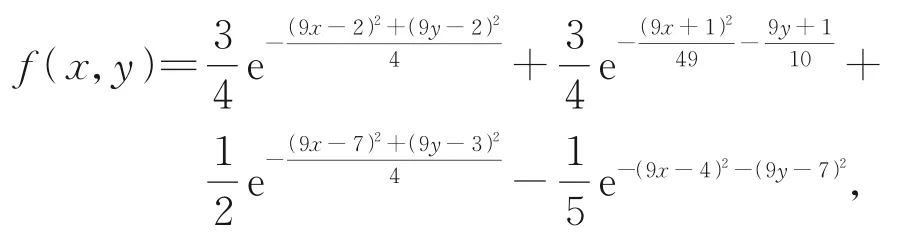
上采样得到42×54个数据点:
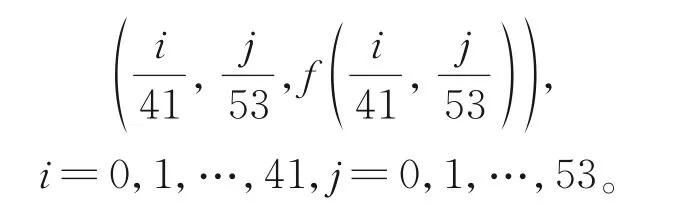
实验参数选取如下:由注1,在利用PGMRES、PPIA 和IPPIA-GMRES 法逼近例1~例4 中数据点时,预处理子的半带宽取值如表1 所示。在测试IPPIA-GMRES 法时,取式(10)中的τk=0.01,取式(12)中的θ=0.85。为方便比较,取IPPIA-CG 法中的τk=0.01,θ=0.85。

表1 例1~例4 中预处理子的半带宽Table 1 Half-bandwidth of preconditioners in examples 1 to 4
在逼近例1~例3 数据点时,PIA、WPIA 和PPIA 法迭代矩阵的谱分布如图1 所示,相应的迭代矩阵的谱半径如表2 所示。可知,与PIA 法和WPIA 法相比,PPIA 法迭代矩阵的大部分特征值向0 方向聚集。PPIA 法迭代矩阵的谱半径明显小于PIA 法和WPIA 法。因为迭代矩阵的谱半径越小,收敛速度越快,所以PPIA 法的收敛速度提升很快。此外,由于迭代矩阵的谱分布更聚集,P-GMRES 法的收敛效果也得到了改善。
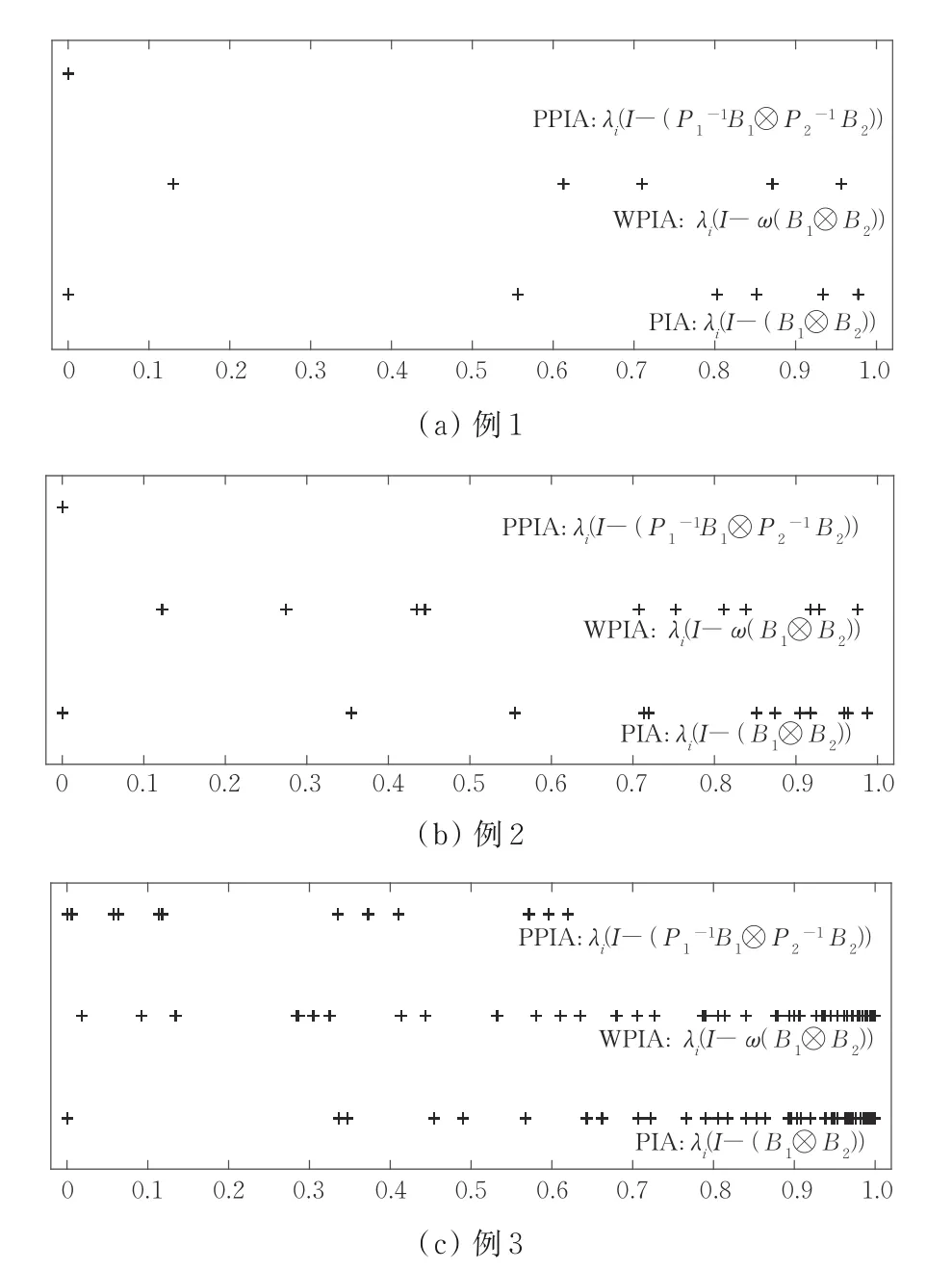
图1 例1~例3 中PIA、WPIA 和PPIA 法迭代矩阵的谱分布Fig.1 Spectral distributions of iteration matrices of PIA,WPIA and PPIA in examples 1 to 3

表2 例1~例3 中迭代矩阵的谱半径Table 2 Spectral radius of iteration matrices in examples 1 to 3
表3~表5 分别为用不同方法迭代逼近例1~例3 中数据点时的插值误差ε和运行时间T,可知,WPIA 法的收敛速度较慢,PPIA 法的收敛速度较快,特别是例1 和例2,用PPIA 法迭代一次就能达到机器精度。同样,在数据点很少时,用GMRES法和P-GMRES 法均能得到精确的插值曲面;随着数据点的增多,2 种方法的插值误差随之减小,PGMRES 法比GMRES 法减小更明显,说明本文提出的预处理子能改善GMRES 法的收敛性。在插值误差几乎相同的情况下,PPIA 法在迭代次数k和运行时间上具有优势,说明本文方法具有计算效率优势。

表3 例1 中WPIA、PPIA、GMRES 和P-GMRES 法的插值误差和运行时间Table 3 Interpolation errors and runtime of WPIA,PPIA,GMRES and P-GMRES in example 1

表4 例2 中WPIA、PPIA、GMRES 和P-GMRES 法的插值误差和运行时间Table 4 Interpolation errors and runtime of WPIA,PPIA,GMRES and P-GMRES in example 2

表5 例3 中WPIA、PPIA、GMRES 和P-GMRES 法的插值误差和运行时间Table 5 Interpolation errors and runtime of WPIA,PPIA,GMRES and P-GMRES in example 3
在逼近例4 中数据点时,由于数据点较多,WPIA 法的收敛速度很慢,PPIA 法得到的插值误差较大,这由预处理子的求逆运算不稳定造成。此时GMRES 法和P-GMRES 法的运算结果亦不理想,可考虑采用非精确求解方法近似求解预处理方程。由表6的数值结果知,在终止阈值θ相同时,IPPIA-CG 法只需迭代1 次(此时,可通过提高内迭代精度增加迭代次数,以减少IPPIA-CG 法的插值误差),IPPIA-GMRES 法需迭代6次,但插值精度也相应提高,说明IPPIA-GMRES 法能更有效地插值较大规模的数据点。在运行时间上,IPPIAGMRES 法虽不及GMRES法和P-GMRES法,但明显优于WPIA法,且IPPIA-GMRES 法的插值误差更小。

表6 例4 中IPPIA-GMRES 法和其他方法的插值误差和运行时间Table 6 Interpolation errors and runtime of IPPIA-GMRES and the other methods in Example 4
用WPIA 法和PPIA 法迭代逼近例1~例3的数据点,得到的Said-Ball 曲面如图2~图4 所示;用WPIA、IPPIA-CG 和IPPIA-GMRES 法迭代逼近例4 中的数据点,得到的Said-Ball 曲面如图5 所示。不难看出,由本文方法生成的张量积型Said-Ball 曲面能快速逼近给定数据点。

图2 例1 中的Said-Ball 插值曲面Fig.2 Said-Ball interpolation patches in example 1

图3 例2 中的Said-Ball 插值曲面Fig.3 Said-Ball interpolation patches in example 2

图5 例4 中的Said-Ball 插值曲面Fig.5 Said-Ball interpolation patches in example 4
5 结论
基于对角补偿约化技术,探讨了求解张量积型Said-Ball 曲面的PPIA法,并用GMRES 法求解预处理方程,得到非精确解,即IPPIA-GMRES 法。相较文献[18]利用共轭梯度法求解预处理方程的方法,本文的非精确求解方法计算量更小,得到的插值曲面精度更高,计算效率也更高。此外,由于本文提出的预处理方法能使配置矩阵的谱分布更集中,在处理规模适当的插值问题时,采用对角补偿预处理子能在一定程度上改善GMRES 法的收敛性。
由于预处理技术能在有效改善非分段(片)基函数的同时配置矩阵的谱分布[19,22],因此本文方法能推广应用于类似曲面(如张量积型Bézier 曲面)PIA法的加速问题。但本文方法也存在局限性,由于分片曲面(如双三次B 样条曲面、NURBS 曲面等)PIA法中的配置矩阵为稀疏矩阵,利用对角补偿约化技术构造的预处理子效果不明显,甚至不起作用。不同于分片插值,本文方法利用一张Said-Ball 曲面对所有数据点插值,具有更高的连续性。未来,将进一步探讨分片曲面PIA 法的加速问题。
