郭守敬创制的景符在笛卡尔坐标系下的工作机理
2022-11-25原杰
原 杰
(1.邢台学院资源与环境学院,河北邢台 054001;2.邢台社会治理研究院,河北邢台 054001;3.邢台市地信与遥感技术应用重点实验室,河北邢台 054001)
郭守敬(1231年—1316年),字若思,邢州邢台县(今河北省邢台市信都区)人。元朝著名的天文学家、数学家、水利工程专家[1],官至太史令、昭文馆大学士、知太史院事,世称“郭太史”,著有《推步》《立成》等十四种天文历法著作[2]。七个世纪之后的今天,郭守敬仍然是邢台市的科技名片;他发明的景符在《元史·天文志》[3]中被记录如下:
“景符之制,以铜叶,博二寸,长加博之二,中穿一窍,若针芥然。以方跂为趺,一端设为机轴,令可开阖,榰其一端,使其势斜倚,北高南下,往来迁就于虚梁之中。窍达日光,仅如米许,隐然见横梁于其中。旧法一表端测晷,所得者日体上边之景。今以横梁取之,实得中景,不容有毫末之差。至元十六年己卯夏至晷景,四月十九日乙未景一丈二尺三寸六分九厘五毫。至元十六年己卯冬至晷景,十月二十四日戊戌景七丈六尺七寸四分。”
在郭守敬取得伟大的成绩之后的几个世纪里,数学和物理学取得了长足的发展。法国哲学家、数学家、物理学家勒内·笛卡尔(René Descartes,1596—1650),对现代数学的发展做出了重要的贡献,因将几何坐标体系公式化而被认为是解析几何之父[4]。在笛卡尔几何坐标系下,郭守敬创制的景符的工作机理,是本文研究重点。
一、方法
(一)中心直线和景符小孔坐标的数学表达
本文选择郭守敬设计制造的四丈高表(见图1a)为研究对象。以表为纵坐标,圭为横坐标,圭和表的交点为原点,建立笛卡尔直角坐标系[5]。在圭表-景符测量系统中,经过景符最后定位后,每日正午的太阳中心(tx,ty)、横梁中心(0,H)、景符中心(m,n)、和横梁中心的影子(x,0)应该在一条直线(本文称为“中心直线”)上。当日期固定后,当天的太阳高度角固定,设为θ,则我们可以给出该中心直线的表达式(见图1b):

图1 文中用到的数学表达对应的图。所有示意图,均比实际角度要大
y=kx+H
(1)
其中,k=tan(180°-θ)=-tanθ。将所有的应变量都换算成以横梁中心高度H为自变量的函数;在y=0,我们有圭表上横梁中心的影子的横坐标
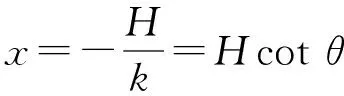
(2)
此即为影长。景符中心的横坐标
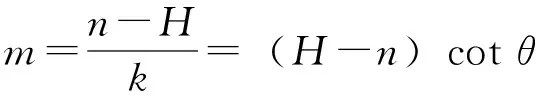
(3)
其中,景符中心的纵坐标n是“铜叶”“中穿一窍”的高度(简称“窍高”)。
因“铜叶”“一端设为机轴,令可开阖”,故其“窍”高度可以变化,变化范围在“‘趺’高(hf)”(铜叶水平时)和“‘趺’高(hf)+‘铜叶’高(ht)的一半”(铜叶垂直时)之间(见图1c右上),即

(4)
其中hf≥0。如果窍的高度n变化,同时m(式(3))也相应变化,此时构成“往来迁就”的动作。
(二)横梁光影特性的数学表达
在高等数学中业已证明[5]:在笛卡尔坐标系中,设有圆(x-a)2+(y-b)2=r2和圆外一点Q:(p,q),则Q点和圆的切线的解析解方程满足
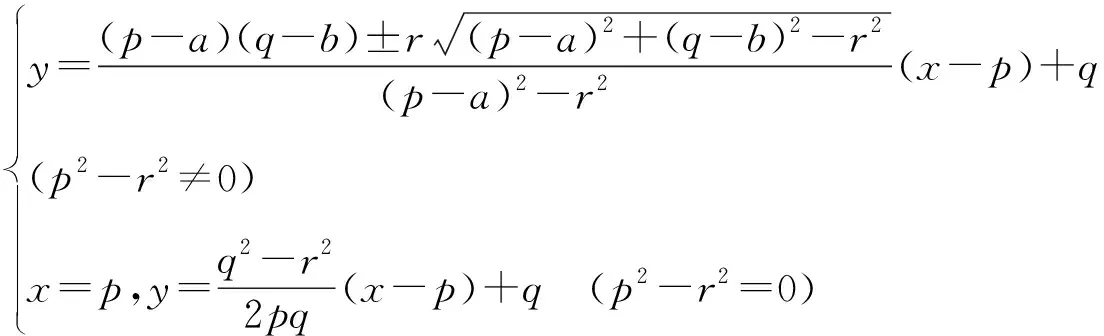
(5)
式(5)的第一个式子对应太阳光斜射的情况,第二个式子对应太阳光直射的情况。按照元朝郭守敬实测的数据,前者可应用在北回归线以北的任何时候的测量中;后者可应用在南北回归线之间,且太阳直射当地的时候的测量[3]。
对于《元史·天文志》记载的北京实测的数据而言,按照小孔成像原理[6,7],从“铜叶”中心引出的“和横梁的圆截面相切的直线方程”符合第一个式子(见图1c),其对应的方程为:
(6)
和
(7)
两式中已带入横梁和“铜叶”的相关参数,rh为横梁的半径。
令y1=0 和y2=0 ,我们得到横梁外边在圭尺上的投影

(8)
和

(9)
显然,因为两式都包括了可以变化的“铜叶”高度n(式(4)),所以x1和x2也是可以变化的。为了研究横梁光影的特性,这里我们定义以下几个变量:
1.描述影宽
Δx=x1-x2
(10)
此式正是郭守敬“实得‘横梁’中景”的宽度,即“不容有毫末之差”的绝对大小。
2.描述圭表测量的相对精度[5]
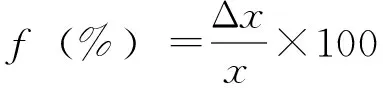
(11)
此式正是郭守敬“不容有毫末之差”与横梁影长的相对值。
3.描述横梁影子对称性(单位为1)

(12)
显然,ry=1的时候,横梁影子中心相对两边对称。
(三)太阳光斑特性的数学表达
在正午时,太阳通过“铜叶”之后,成像为一个近似椭圆[7,8](见图1b右上),其短轴的长度(按照下述的“仅如米许”的测量标准)等于米粒长度[3];其长轴方向的特性,描述了光斑随景符高度调节时候表现的特征。在研究太阳的光斑的时候,这里假设一个虚太阳,其中心在(0,H)点;在此假设下,研究太阳在横坐标上的投影的方法,和横梁的研究方法相同(见图1c);除了太阳半径rt有变化外,式(5)中其他参数不变。进一步,如何给出太阳在(0,H)点的视半径rt,就成了解决问题的关键。从横梁中心的影子(x,0),引出一个视角度为0.5°(=0.25°×2)[7]的圆,其圆心在横梁中心;并同时引出一条和横梁上沿相切的线(见图1d)。按照三角学知识[5],我们有

(13)
在横梁和圭尺组成的三角形中有

(14)
结合式(13)和(14),因为L相等,我们有
(15)
根据式(5)、(8)和(9),我们有太阳光斑的外边的横坐标:

(16)
和

(17)
同样我们可以给出
1.光斑的大小,即水平长度:
Δt=t1-t2
(18)
郭守敬记录的光斑“仅如米许”,按照现代小米的平均直径1.2mm[9]计算,其对应的景表尺长度为0.0049尺(=0.12cm/24.525cm,24.525cm为现代计量单位下1景表尺[7]的长度);该长度是景符在移动过程中,读取相关数值和计算对应精度的一个重要限制性条件;“许”字,说明实际值与0.0049相比,可以有极微小的偏离。
2.光斑偏离圆形的度量方法为(单位为1)

(19)
显然,当rt=1时,横梁影中心平分光斑,此时光斑为圆形;同时达到“隐然见横梁于其中”。
3.横梁影子和光斑大小的比值(单位为1)

(20)
4.光斑右侧宽度和左侧宽度之比(单位为1)

(21)
二、计算结果
本文选择《元史·天文志》[3]中记录景符的相关信息,来恢复记录的圭表测量值。参数选择:高表的高度用40尺(4丈),横梁的半径0.15尺,地理位置选择北京,北京夏至日的太阳高度角用72.81637°,冬至日的太阳高度角用27.53035°。根据本文方法计算结果见表1和图2、3;为方便对比,表内有效数字取小数点后8位;如无特别说明,前述定义的比例变量单位为1,长度单位为尺,长度小数点后的单位依次为寸、分、厘、毫(研究到毫的水平,就足以复原《元史》的记录了)。

表1 夏至日和冬至日,透过景符的光斑“仅如米许”时,计算获得的结果

图2 夏至日,景符高度从0增加到0.6尺的计算结果。每个图中显示了“如米许”光斑时候的数值。

图3 冬至日,景符高度从0增加到0.6尺的计算结果。每个图中显示了“如米许”光斑时候的数值。
夏至日结果:横梁中心的影子为12.36954597尺,和《元史》中记录的数据相符。景符窍高沿中心直线“往来迁就”从0到0.6尺的高度上,寻找仅有米粒大小光斑的过程中,所有应变量都是线性地变化:影宽从0增加到0.005尺,相对精度从0增加到0.004,横梁影子对称性从0.99779减小到0.99775,光斑的大小从0增加到0.006尺,光斑偏离圆形从1.002700增加到1.002745,横梁影子和光斑大小的比值从0.82107343减小到0.82107333,光斑右侧宽度和左侧宽度之比从1.00492增加到1.00501尺。当发现光斑为0.00489017景表尺时,窍高为0.506,影宽为0.00401519,相对精度为0.03246025,横梁影子对称性为0.99775841,光斑偏离圆形为1.00273688,横梁影子和光斑大小的比值为0.82107335,光斑右侧宽度和左侧宽度之比为1.00498966。
冬至日结果:横梁中心的影子为76.74000932尺,和《元史》中记录的数据相符。景符窍高沿中心直线“往来迁就”从0到0.6尺的高度上,寻找仅有米粒大小光斑的过程中,所有应变量都是线性地变化:影宽从0增加到0.01尺,相对精度从0增加到0.014,横梁影子对称性从0.99387减小到0.99326,光斑的大小从0增加到0.025尺,光斑偏离圆形从1.01688增加到1.01714,横梁影子和光斑大小的比值从0.3972221减小到0.3972212,光斑右侧宽度和左侧宽度之比从1.02368增加到1.02403尺。当发现光斑为0.00489614景表尺时,窍高为0.12,影宽为0.00194485,相对精度为0.00253434,横梁影子对称性为0.99335149,光斑偏离圆形为1.01693453,横梁影子和光斑大小的比值为0.39722193,光斑右侧宽度和左侧宽度之比为1.02374088。
三、讨论
结合前面的理论,并对比夏至日和冬至日的数据,我们发现:
1.在两至日的北京,使用景符都能够找到“仅如米许”的光斑,能够计算出对应的影长,说明《元史》记载无误,同时与理论相互佐证;
2.两至日内的影宽,随太阳高度角的变化而变化,并不是一个绝对值;太阳高度角越小,影宽越窄。计算获得的影宽和现代(文献[7]内表1记录的冬至日附近)实际测量的0.00x(x表示对应的小数位,下同)尺水平吻合;
3.在现代科学下,测量相对精度都很高,在0.0x%水平及以下。测量相对精度随太阳高度角的变化而变化,并不是一个绝对值;太阳高度角越小,相对精度越高;
4.横梁影子对称性为0.99x水平及以下,光斑对称性在1.0x水平及以下,光斑右/光斑左的比例在1.0x水平及以下。它们都非常接近于1,但不等于1,说明整个光斑和横梁体系在“仅如米许”时候,是一个非常接近于圆的椭圆。实际观测中,在肉眼能区别的范围内,可以认为光斑长轴方向始终是平分的,在达到“米许”的尺寸时,整个横梁平分光斑;
5.横梁影宽和光斑大小的比值,随太阳高度角的增大而增大;说明在手动记录横梁位置的时候[3,10],冬季需要用到比夏季更细的笔来记录。
四、结论
本文结论如下:
1.郭守敬创制的景符在笛卡尔坐标系下的工作原理,即“一端设为机轴,令可开阖,榰其一端,…,往来迁就于虚梁之中。窍达日光,仅如米许,隐然见横梁于其中”,可以用高等数学精确表达;
2.新的数学公式准确地复现了《元史》中记录的至元十六年夏至日和冬至日的日影长度,发现用景符记录横梁位置的测量精度,在“不容有毫末之差”的“毫”水平上;
3.新的数学公式可以更深入且定量地研究横梁的影宽、相对精度、横梁影子对称性、光斑的大小、光斑偏离圆形、横梁影子和光斑大小的比值、光斑右侧宽度和左侧宽度之比等7个特征信息。这些特征信息都是太阳高度角和窍高的函数,意味着研究一年内每日的日影记录时,需要有不同的特征信息来深入分析;为从新角度研究与景符相关的工作,提供了思路。作为例子,夏至日和冬至日的各个特征信息有明显的区别。
