中央调剂制度下养老金替代率影响因素研究
2022-11-25李明桥严怡梅
李明桥,严怡梅
(西南石油大学 马克思主义学院,四川 成都 610500)
一、引言
企业职工基本养老保险基金中央调剂制度是省级统筹向全国统筹过渡的标志。通过中央调剂制度实现了部分养老保险基金由中央统一调剂使用,这有助于均衡地区间基金负担,提高养老保险基金整体抗风险能力。虽然中央调剂制度发挥了跨省调剂养老保险基金的作用,但是并未改变省级政府承担养老保险基金缺口的主体责任,例如国发〔2018〕18号文件规定:“中央政府在下达中央财政补助资金和拨付中央调剂金后,各省份养老保险基金缺口由地方政府承担。”养老保险基金缺口既取决于离退休人员的养老金支出,又取决于养老保险基金收入,即在职参保职工的缴费收入和中央调剂金净拨付额。当养老保险基金支出高于收入时,则基金缺口可先由中央财政补助资金进行填补,不足部分再由养老保险基金累计结余或地方财政弥补。
因为中央调剂制度上解比例决定了各省份中央调剂金净拨付额大小,所以现有文献侧重于研究上解比例对养老保险基金收入再分配的影响。中央调剂制度既有利于降低养老保险基金收不抵支省份赤字规模,又有助于推迟累计赤字时点,因此提高上解比例有利于增强养老保险基金省际间再分配(石晨曦和曾益,2019)[1]。然而,如果中央调剂制度上解比例过高,那么会导致不公平的逆向调节,反之如果上解比例过低中央调剂制度省际再分配效应较弱(边恕和李东阳,2019)[2]。理论上讲应该存在上解比例“临界值”使得基金调剂规模由贡献省份流向受益省份是适度的,这个临界值既能避免鞭打快牛,也能保证对受益省份的补助金额有节有度(郭秀云和邵明波,2019)[3]。
关于中央调剂制度上解比例的研究成果丰硕,但是鲜有文献研究中央调剂制度上解比例与养老保险缴费率的关系。本文立足于研究中央调剂制度下养老金替代率的影响因素,尤其是上解比例和缴费率两个因素。研究目的是一方面分析养老金替代率的影响因素,另一方面在新冠肺炎疫情对中国经济产生负向冲击背景下,探讨中央调剂制度下养老保险缴费比例是否存在临时性下调空间,以缓解企业生产负担从而实现“六保”中的保障居民就业的目标。
本文提出能否临时性下调养老保险缴费率的原因在于:学界通过OECD国家横向比较(杨燕绥等,2015;苏中兴,2016)[4-5]与模型拟合最优缴费率(柳清瑞等,2013;康传坤和楚天舒,2014)[6-7]都表明中国养老保险缴费率合理区间应为10%~22%。政府部门于2018年和2019年连续发布人社部〔2018〕5号文件和国办〔2019〕3号文件降低养老保险缴费率,现阶段养老保险缴费率已经降至24%,其中单位和个人分别负担16%和8%,这个缴费率已经接近学界的缴费率合理区间上限,而且调低了养老保险就业人员平均工资计算口径,在此背景下是否还具备临时性下调养老保险缴费率空间是一个值得研究的问题。
本文构建的跨期迭代(OLG)模型包括个人、企业和政府三部门,其中个人和企业的目标分别是追求效用最大化和利润最大化,政府部门的目标是实现养老保险预算平衡也就是养老保险基金收入等于支出。本文基金收入仅考虑养老保险缴费收入和中央调剂金净拨付额,不涉及财政补贴和养老保险基金累计结余,而基金支出则为离退休人员领取的养老金。如果政府实现养老保险预算平衡并且市场处于出清状态,那么经济实现了均衡状态。这表明当养老保险预算平衡下的养老金替代率等于市场出清下的养老金替代率时,则经济处于均衡状态。具体模型构建过程如下文所示。
二、构建理论模型
(一)基本模型设定
1.个人行为
假设代表性个体经历两个时期:工作期(t)和退休期(t+1)。在工作期,个体一方面要工作,以获取工资收入,另一方面要决定当期消费(Ct)和储蓄(St),并且按照国家规定缴纳养老保险费。进入老年期之后,个体主要依靠养老金和储蓄生活。假定效用函数为对数形式,则i省份代表性个体的效用函数为Uit=ln(Cit)+βln(Cit+1),其中β为反映时间偏好的贴现因子。在工作期,i省份代表性个体在完全竞争市场条件下获取工资收入为wit,并按照国家当期规定的缴费率τt缴纳养老保险费,则个体可支配收入为(1-τt)wit。可支配收入既要满足当期消费又要进行当期储蓄,为退休生活做准备。退休后个体消费(Cit+1)既来源于个体的养老金收入(Pit+1),又来源于工作期的储蓄收益(1+r)Sit,其中r是利率。综上所述,代表性个体的跨期预算约束为式(1)和式(2)。根据跨期预算约束条件得出个体效用最大化的消费和储蓄方程分别为式(3)和式(4)。
Cit+Sit=(1-τt)wit
(1)
Cit+1=(1+r)Sit+Pit+1
(2)
(3)
(4)
2.企业行为
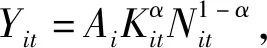
(5)
(6)
3.政府部门
如果考虑财政补贴问题,那么研究更为复杂,为了便于说明问题,本文研究对象为现收现付制下没有财政补贴的养老保险制度。本文使用现收现付制的原因在于:虽然我国城镇职工养老保险制度是统账结合的部分积累制度,但是养老保险制度改革成本转嫁到社会保障部门,这导致城镇职工养老保险制度个人账户基金用于支付养老金,从而使得个人账户空账运行,这说明中国养老保险名义上是部分积累制,实际上是现收现付制。在此前提下i省t期养老保险实现预算平衡的等式为式(7)。等式左边为养老保险基金收入,由工作期个体缴纳的养老保险费(τtwitNit)和中央调剂金净拨付额(Dit-UPit)构成。式(7)右边的养老保险基金支出等于退休期的代表性个体养老金收入(Pit)与退休期人数(RNit)的乘积。由式(7)可得出式(8)前半部分,在假设人口增长率为n的条件下,则有(1+n)=Nit/RNit,由此可得式(8)后半部分。中央调剂金净拨付额(Dit-UPit)由上解额UPit和下拨额Dit构成,根据国发〔2018〕18号文件可知上解额和下拨额的表达式为式(9),其中Rt表示t期的上解比例。由式(8)、式(9)和式(10)可得出式(11),其中dt表示参保退休人员的中央调剂金人均拨付额,其函数形式为dt=(Dit/RNit)=dt(wit,Rt,Nit,RNit),分别求偏导可得(αdt/αwit)>0、(αdt/αRt)>0、(αdt/αNit)>0和(αdt/αRNit)<0。git表示i省t期的上解额占中央调剂金比例,由偏导可得(αgit/αwit)>0和(αgit/αNit)>0。fit表示i省t期的参保退休人员占全国比例,由偏导可得(αfit/αRNit)>0。假设养老金增长率为v,则Pt+1=(1+v)Pt,那么由式(11)可推导出在中央调剂制度下政府实现养老保险预算平衡的养老金替代率T1的表达式为式(12)。值得一提的是,T1仅能确保中央调剂制度下政府实现养老保险预算平衡,但不能确保市场处于均衡状态。
τtwitNit+Dit-UPit=PitRNit
(7)
(8)
(9)
(10)
(11)
(12)
(二)均衡状态下的养老金替代率
在市场出清条件下,当期储蓄全部转换为下一期的资本投入,即Kit+1=NitSit,不难得到式(13)。由式(4)和式(13)可得市场出清时养老金替代率T2的表达式为式(14)。Imrohoroglu等(1995)[8]研究发现:在缺乏养老保险制度背景下,年轻人为保障自己老年生活水平的过度储蓄行为导致资本回报率下降,从而降低了整体社会福利水平。现收现付制养老保险有助于降低居民储蓄水平,从而提高了资本回报率,但是较高的养老金替代率又会导致储蓄不足,从而引起资本存量低于最优水平,该研究得出现收现付制养老保险的最优养老金替代率为30%左右,由此可知在养老保险背景下的最优养老金替代率T2>0。
因为假定生产技术不变,所以经济处于稳态下的人均资本Kit+1为常数,则由式(5)和式(14)可得式(15)。当养老金替代率满足条件T1=T2时,此时替代率既实现了政府养老保险预算平衡又保证了市场出清,这个替代率为均衡状态下的养老金替代率。如果T1>T2表明养老保险预算平衡的养老金替代率高于市场出清时的替代率,那么政府把养老金替代率由T1下调为T2,此时既保证市场出清又实现了养老保险预算盈余。如果T1 (1+n)kit+1=Sit (13) (14) (15) 参照郑秉文(2019)[9]的研究方法,可把养老金替代率的影响因素归为人口因素、制度因素和经济因素三类。本文跨期迭代模型中的人口因素包括参保劳动人口Nit和参保退休人口RNit;制度因素由上解比例Rt和养老保险缴费率τt构成;经济因素则为工资wit和利率r。根据式(12)和式(15)可得出各影响因素判断表,如表1所示,可分为两种影响类型:类型一,只影响一个替代率的利率因素和上解比例因素;类型二,同时影响两个替代率的因素,包括参保劳动人口Nit、参保退休人口RNit、养老保险缴费率τt和工资wit。本文将依次分析这两种类型的影响因素。 研究影响因素的前提条件是弄清楚养老保险中央调剂制度如何影响养老金替代率的。因为中央调剂制度的上解额和下拨额是养老保险预算平衡方程的组成部分[式(7)或者式(12)],但不是市场出清方程的组成部分[式(13)或者式(15)],所以中央调剂制度仅能影响养老保险预算平衡的养老金替代率T1。由式(12)可知,i省t期中央调剂金上解额的全国占比(git)和参保退休人口的全国占比(fit)共同决定了养老保险预算平衡下的养老金替代率变化方向。当git>fit,即[1-(git/fit)]<0时,则i省t期为养老金净流出省份,由式(12)可得中央调剂制度降低了i省t期预算平衡下的养老金替代率;反之当git 表1 养老金替代率的影响因素判断表 一方面,利率越高,市场出清状态下的养老金替代率越高。由式(14)的养老金替代率T2对利率求偏导可得式(16),由上文可知,T2>0,则可推导出(αT2/ar)>0,这表明利率越高,养老金替代率T2越大。另一方面,利率不影响养老保险预算平衡的养老金替代率T1。如式(12)所示,利率不是替代率T1的组成部分,故不对T1产生影响。由此可得利率影响养老金替代率。如图1所示,当利率r=r*时,则T1(r*)=T2(r*),此时同时实现了养老保险预算平衡和市场出清的均衡状态。当利率r=r2(r2取值范围是大于参数r*的数值)时,则T1(r2) 图1 利率影响因素图 (16) (17) (18) 因为中央调剂制度的上解比例是养老保险预算平衡方程式(12)的组成部分,并且上解比例越高,中央调剂金的人均下拨额越大,即(αdt/αRt)>0,所以上解比例对养老金替代率T1的影响取决于调剂金流动方向。当i省t期为调剂金净流入省份,即[1-(git/fit)]>0时,则式(12)T1对Rt偏导表达式[(1+v)(αdt/αRt)(1-git/fit)/wit]>0,这表明上解比例越高,调剂金净流入省份的替代率T1越大;反之,当i省t期为调剂金净流出省份,即[1-(git/fit)]<0时,则T1对Rt的偏导表达式[(1+v)(αdt/αRt)(1-git/fit)/wit]<0,这表明上解比例越高,调剂金净流出省份的替代率T1越小。如式(14)所示,上解比例不是养老金替代率T2的组成部分,所以上解比例不影响市场出清的养老金替代率T2。由此可得,上解比例对调剂金净流入省份替代率的影响,如图2所示。当上解比例R=R2时,则T1(R2)>T2(R2),如果政府为了市场出清而实施养老金替代率T2(R2),那么调剂金净流入省份实现养老保险预算盈余,这表明上解比例R2导致中央调剂制度对i省t期养老金的调入过度,上解比例R2偏高。当上解比例R=R1时,则T1(R1) 图2 上解比例影响因素图 注:图2中研究对象是中央调剂金净流入省份 当上解比例R=R*时,则T1(R*)=T2(R*),此时同时实现了养老保险预算平衡和市场出清,经济处于均衡状态,上解比例R*为政府预算平衡和市场出清的最优上解比例。 就参保劳动人口Nit对养老金替代率T1的影响而言,由式(12)替代率T1对Nit求偏导可得式(17)。给定参保退休人口RNit,则参保劳动人口Nit增加,也就是人口增长率n[=(Nit/RNit)-1]上升,由此推导出式(17)右边第一项(1+v)τt(αn/αNit)>0,这表明现收现付制下增长的参保劳动人口提高了养老保险基金收入,从而提高了养老保险预算平衡下的养老金替代率T1,因此式(17)中的τt(αn/αNit)可称为参保劳动人口增长引起的人口红利效应。式(17)右边方括号反映了增加的参保劳动人口通过中央调剂制度对养老金替代率T1的影响,本文称为参保劳动人口增加引起的中央调剂效应,它由参保劳动人口增加引起的中央调剂净收益效应[(αdt/αNit)(1-git/fit)]和中央调剂贡献效应[(dt/fit)(αgit/αNit)]构成。表达式[(αdt/αNit)(1-git/fit)]之所以称为净收益效应,是因为表达式(1-git/fit)与0的关系决定了i省t期的调剂金是净流入还是净流出,从而决定了参保劳动人口因素对替代率T1的影响。当i省t期增加的参保劳动人口提高了中央调剂金人均拨付额,即(αdt/αNit)>0时,如果[1-(git/fit)]>0,即i省t期为调剂金净流入省份,那么增加的参保劳动人口所提高的养老保险基金收入就不会通过中央调剂制度而调出,从而提高了该省份养老金替代率T1。同理,i省t期为调剂金净流出省份,那么增加的参保劳动人口所提高的养老金保险基金收入则会通过中央调剂制度而调出,从而降低了该省份养老金替代率T1。表达式[(dt/fit)(αgit/αNit)]之所以称为中央调剂贡献效应,是因为表达式(αgit/αNit)反映了参保劳动人口增长提高了i省t期中央调剂金上解额对全国的贡献,从而降低了该省份养老金替代率T1。综上所述,参保劳动人口因素对养老金替代率T1的影响路径如表2上半部分所示。 就参保劳动人口因素Nit对养老金替代率T2的影响而言,参保劳动人口增长既影响人口增长率,又影响人均资本存量。一方面给定参保退休人口RNit,参保劳动人口Nit增加,实际上就是人口增长率n上升;另一方面由市场出清式(13)可得,如果储蓄不变,那么人口增长率n上升将导致人均资本kit+1下降。然而当储蓄不变时,说明人口增长(1+n)与人均资本kit+1的乘积始终不变,因此根据式(14)可得:当储蓄不变时,参保劳动人口因素Nit对养老金替代率T2不产生影响。同理,当储蓄增加时,参保劳动人口的增长将会降低市场出清养老金替代率T2,反之,当储蓄减少时,则会提高养老金替代率T2。 表2 人口因素对养老金替代率T1的影响效应分析表 就参保退休人口RNit对养老金替代率T1的影响而言,由式(12)替代率T1对RNit求偏导可得式(18)。在参保劳动人口给定条件下,参保退休人口越多的省份人口增长率越低,即(αn/αRNit)<0,由此可知式(18)第一项(1+v)τt(αn/αRNit)<0,这表明在现收现付制的养老保险基金收入不变背景下,参保退休人口越多的省份养老金替代率越低,说明人口红利效应为负值。同理,参保退休人口也能通过中央调剂制度影响养老金替代率T1,本文称为参保退休人口因素的中央调剂效应,它由中央调剂净收益效应[(αdt/αRNit)(1-git/fit)]和中央调剂再分配效应[(dtgig/(fit)2)(αfit/αRNit)]构成。表达式[(dtgig/(fit)2)(αfit/αRNit)]之所以称为再分配效应,是因为i省t期参保退休人口越多,则该省份参保退休人口的全国占比fit越高,即(αfit/αRNit)>0,那么中央调剂制度的养老金下拨额越大,因此中央调剂再分配效应提高了养老金替代率T1。参保退休人口越多,则中央调剂金人均下拨额越低,即(αdt/αRNit)<0,所以当i省t期为中央调剂金净流入省份,即(1-git/fit)>0时,则有中央调剂净收益效应[(αdt/αRNit)(1-git/fit)]<0,这表明参保退休人口因素的中央调剂净收益效应导致中央调剂金净流入省份的养老金替代率T1下降。反之,当i省t期为中央调剂金净流出省份,即(1-git/fit)<0时,则有中央调剂净收益效应[(αdt/αRNit)(1-git/fit)]>0,这表明参保退休人口因素的中央调剂净收益效应提高了中央调剂金净流出省份的养老金替代率T1,参保退休人口对养老金替代率T1的影响路径如表2下半部分所示。 就参保退休人口因素RNit对养老金替代率T2的影响而言,参保退休人口增长既影响人口增长率又影响人均资本存量。一方面给定参保劳动人口Nit,参保退休人口RNit增加,实际上就是人口增长率n下降;另一方面由市场出清式(13)可得,如果储蓄不变,那么人口增长率n下降将导致人均资本kit+1上升。然而当储蓄不变时,说明人口增长(1+n)与人均资本kit+1的乘积始终不变,因此根据式(14)可得:当储蓄不变时,参保退休人口因素RNit对养老金替代率T2不产生影响。同理,当储蓄增加时,参保退休人口的增长将会降低养老金替代率T2,反之,当储蓄减少时,则提高了养老金替代率T2。 就养老保险缴费率τt对养老金替代率T1的影响而言,一方面,当政府下调养老保险缴费率τt时,养老保险基金收入下降,在现收现付制养老保险预算平衡的前提下养老金替代率T1下降,也就是式(12)T1对τt求偏导,可得∂T1/∂τt=(1+v)(1+n)>0。另一方面,式(12)方括号中的第二项[dt(1-git/fit)/wit]不含缴费率因素τt,这表明缴费率并不会通过中央调剂制度影响养老金替代率T1。就养老保险缴费率τt对养老金替代率T2的影响而言,由式(14)T2对τt求导,可得∂T2/∂τt=-β(1+r)<0,这表明当政府下调养老保险缴费率τt时,市场出清的养老金替代率T2上升。缴费率影响替代率如图3所示,如果初始缴费率为τ*,那么T1(τ*)=T2(R*),说明养老保险缴费率τ*同时实现了政府养老保险预算平衡和市场出清。当政府把缴费率由τ*下调为τ1时,则T1(τ1) 图3 缴费率影响因素图 就工资wit对养老金替代率T1的影响而言,由式(12)替代率T1对工资wit求偏导,可得式(19)。由式(19)可知,工资通过中央调剂效应影响养老金替代率T1,工资的中央调剂效应由净收益效应[(α(dt/wit)/αwit)(1-git/fit)]和贡献效应[(dit/witfit)(αgit/αwit)]构成。就净收益效应而言,由式(9)可得式(20),再由式(20)的(dt/wit)对工资wit求偏导,推导出式(21)。由此可知,工资增长虽然提高了中央调剂金人均拨付额dt,但是人均拨付额的增幅小于工资增幅,从而导致(dt/wit)下降,所以当i省t期为中央调剂养老金净流入省份,即(1-git/fit)>0时,则工资的中央调剂净收益效应[α(dt/wit)/αwit](1-git/fit)<0,从而降低了i省t期养老金替代率T1。反之,当i省t期为中央调剂养老金净流出省份,即(1-git/fit)<0时,则工资的中央调剂净收益效应[α(dt/wit)/αwit](1-git/fit)>0,从而提高了i省t期养老金替代率T1。由中央调剂贡献效应[(dt/witfit)(αgit/αwit)]>0可知,i省t期增长的工资提高了该省对中央调剂养老金的贡献,从而降低了i省t期养老金替代率T1。就工资wit对养老金替代率T2的影响而言,由式(15)可知,工资增长降低了市场出清的养老金替代率T2。 (19) (20) (21) 上文定性分析了人口因素、制度因素和经济因素对养老金替代率的影响。接下来的数值模拟一方面为了考察各省份养老保险预算平衡的替代率T1和市场出清替代率T2的分布状况,从而判断哪些省份的替代率更加趋近于均衡状态(T1=T2)、哪些省份偏离均衡状态更严重;另一方面,通过数值模拟确定最优的上解比例Rt和缴费率τt,以使各省份替代率T1和T2更为相近,从而实现养老金替代率更加趋近于均衡状态。 数值模拟的数据来源于中国统计年鉴和中国劳动统计年鉴2019年统计数据。就变量选取而言,本文跨期迭代模型变量包括各省份生产技术参数,即式(5)中的参数Ai、参保劳动人口Nit、参保退休人口RNit和工资wit。首先,参照Cipriani(2016)[10]的研究方法,为了反映各省份生产技术差异,本文先测算出2019年各省份全要素生产率,以全要素生产率均值为基础得出各省份全要素生产率的相对值,再把现有文献估算出的生产技术参数A和各省份全要素生产率的相对值相结合作为生产技术代理变量。其次,根据中国劳动统计年鉴2019年的城镇职工基本养老保险参保人数和离退休人数(RNit)推算出参保劳动人口Nit。最后把中国劳动统计年鉴2019年各省份城镇单位就业人员平均工资作为工资wit代理变量。 本文跨期迭代模型参数包括上解比例Rt、养老保险缴费率τt、人口增长率n、时间偏好贴现因子v、利率r和资本产出弹性α。以现有文献为基础,结合中国实际情况,本文参数取值如表3所示。(1)因为人社部将2018年、2019年和2020年中央调剂制度的上解比例依次设为3%、3.5%和4%,所以本文上解比例设为3.5%。(2)依据国办发〔2019〕13号文件规定,养老保险单位和个人缴费率分别为16%和8%,故本文缴费率设定为0.24。(3)以2019年人口自然增长率0.334%为参数值。(4)因为养老金增长率将会与社会平均工资增长率挂钩(郑秉文,2019)[9],所以本文设定为3%。(5)时间偏好贴现因子设为0.6892(Prettner和Werner,2016)[11]。(6)利率以现阶段五年期利率3%为准。(7)根据现有文献(Croix等,2003;万春林等,2021)[12-13]将资本产出弹性设为0.33。 表3 模型参数取值 基于上述参数值和变量对理论模型的式(12)和式(15)进行数值模拟,根据模拟结果绘出各省份养老金替代率分布状况如图4所示,图中实线表示替代率T1=T2,由图4可知:其一,模型拟合的养老金替代率T1相对于实际替代率偏低。实际替代率高于模型拟合替代率T1的原因:一方面归因于实际养老保险预算平衡的基金支付能力由保费收入、财政补贴和基金累计结余三个部分构成,而本文因研究需要仅考虑了养老保险预算平衡的保费收入。另一方面也归因于本文工资为中国劳动统计年鉴的城镇单位就业人员平均工资,而养老保险实际缴费工资基数偏低。 其二,中央调剂养老金净拨付额与替代率T1正相关,这与上解比例越高中央调剂养老金净流入省份替代率T1越大,净流出省份替代率T1越小的定性分析结论一致。图4的中央调剂养老金净流出最高的广东和北京替代率T1较低,而养老金净流入最高的辽宁和黑龙江替代率T1较高。图5描绘了中央调剂养老金净拨付额与养老金替代率T1关系的散点图,虚线上方省份为中央调剂养老金净流入省份,反之则为净流出省份,对散点拟合结果为图中实线并且拟合的调整R方为0.8064,这表明中央调剂养老金净拨付额与替代率T1显著正相关。值得一提的是,养老金替代率与平均工资共同决定了参保退休人员的养老金收入,替代率T1越高并不意味着养老金收入越高,如图4模型拟合的黑龙江和北京养老金替代率T1分别为58.16%和25.38%,而两者参保退休人员养老金平均年收入分别为39791元和42334元,两者反差归因于北京平均工资166803元,远高于黑龙江68416元。 其三,各省份偏离均衡状态的程度存在明显差异。如上文所述,均衡状态是指养老保险预算平衡替代率T1与市场出清替代率T2相等状态。因为图4中实线表示了替代率T1等于T2,即均衡状态,所以各省份替代率分布越接近实线,越趋近于均衡状态。由图4可知,多数省份趋近于均衡状态,但也有些省份严重偏离均衡状态,这些省份为东三省和中央调剂金净流出较多的北京和广东。为了直观反映各省份与均衡状态的偏离程度,本文绘制了图6,图中横轴为养老金替代率的差值,当差值的绝对值越小时,说明该省份越趋近于均衡状态。根据替代率T2与T1之差的绝对值大小可把各省份划为三类:一类省份趋近于均衡状态,即替代率之差的绝对值小于0.02,这类省份包括图6的山西,上至江西。除河北之外这类省份替代率T2小于T1,这表明如果政府把养老保险替代率下调为市场出清替代率T2,则政府养老保险预算盈余。二类省份明显偏离均衡,即替代率差值的绝对值处于0.02至0.06区间,这类省份包括图6的四川,上至甘肃。其余省份即图6中的黑龙江,上至广东,为三类省份,这类省份严重偏离均衡状态,即替代率的差值绝对值高于0.06。 图4 养老金替代率分布图 图5 调剂金净拨付额与替代率T1分布图 图6 各省份偏离均衡状态分布图 学界和政界都认为我国养老保险缴费率偏高。一方面通过OECD国家横向比较与模型拟合的最优缴费率都表明中国养老保险缴费率合理区间应为10%~22%。另一方面人社部发〔2018〕5号文件和国办发〔2019〕3号文件表明政府采取渐进方式降低养老保险缴费率,现阶段养老保险缴费率为24%,其中单位和个人分别负担16%和8%。 结合养老保险缴费率的学界研究成果和政界实施状况,本文研究的缴费率区间设为10%~24%。通过模型拟合各个缴费率下的最优上解比例,模型拟合具体步骤如下:第一步,确定上解比例的下限、上调比例和上限。一方面由于人社部规定2020年上解比例为4%,故本文上解比例下限为4%;另一方面依据人社部在2018年至2020年期间上解比例每年上调0.5个百分点,本文上调比例设为0.5%。就最大上解比例MR而言,中央调剂养老金最大上解额为养老保险缴费收入,其表达式为0.9witNitMR=witNitτt,由此可得最大上解比例表达式MR=τt/0.9。第二步,确定选取最优上解比例的规则。本文以满足式(22)的上解比例作为最优上解比例R*,这是因为式(22)反映了在上解比例Rt下各省份偏离均衡的平均程度。如果缴费率τt下的上解比例R*实现了式(22)最小化,那么这两者组合(τt,R*)使得各省份总体上最趋近于政府养老保险预算平衡和市场出清的均衡状态,该组合就是缴费率τt下的最优组合。 (22) 通过模型拟合出最优组合与均衡偏离程度如图7所示,图中三角形表示各种最优组合的均衡偏离程度,也就是式(22)的取值。由图7可知:其一,如果政府逐渐下调养老保险缴费率,那么最优组合的上解比例将上升。如图7所示,当缴费率处于21%~24%区间时,最优上解比例始终为4%,当缴费率由20%逐渐下调至11%时,则最优上解比例由4.5%上升至11.5%。其二,下调养老保险缴费率将导致偏离均衡程度更严重。如图7所示,当政府逐渐下调养老保险缴费率,即使在最优组合下均衡偏离程度也由5.8%上升至36.2%,这表明随着缴费率的逐渐下调,政府养老保险预算平衡替代率T1与市场出清替代率T2的偏离程度越严重。政府逐渐下调缴费率会导致一些省份替代率的差值(T2-T1)越来越大,如果政府为了市场出清把养老金替代率设为T2,那么养老保险存在预算赤字,这就需要财政补贴或者动用养老保险基金累计结余填补赤字缺口。由此可知,虽然下调养老保险缴费率有助于减轻企业负担,但是也要关注下调缴费率对养老保险预算平衡和市场出清的不利影响。如果政府财政负担压力较小或者养老保险基金累计结余充足,那么下调缴费率导致的养老保险预算赤字问题就容易解决。反之,当政府财政赤字严重并且养老保险基金累计结余较低时,下调养老保险缴费率的政策并不可取。根据人社部统计公报可知,2020年全年基本养老保险基金收入49229亿元,基金支出54656亿元。虽然受新冠肺炎疫情影响2020年基本养老保险预算赤字5427亿元,但是2020年末基本养老保险基金累计结余仍然高达58075亿元,这表明我国仍有下调养老保险缴费率的空间。 图7 最优制度因素组合与均衡偏离程度分布图 数值模拟的缴费率与上解比例最优组合关系是否具有稳健性是一个值得研究的问题。本文从以下三个方面来探讨缴费率与上解比例最优组合关系的稳健性。其一,把数值模拟的城镇单位就业人员平均工资调整为养老保险实际缴费平均工资进行稳健性检验。根据中国劳动统计年鉴2019年基本养老保险基金收入和在职参保人数推算出人均缴费额,再结合缴费率24%得出全国实际缴费平均工资,在此基础上用实际缴费平均工资除以全国城镇单位就业人员平均工资,得出养老保险征缴率,用各省份城镇单位就业人员平均工资乘以征缴率即为各省份实际缴费工资。数值拟合结果如图8所示,调整养老保险缴费工资基数并没有改变养老保险缴费率与上解比例最优组合的反向变化关系。其二,由于人口政策松动,本文把人口自然增长率由2019年的0.334%上调为0.5%,数值拟合结果(图9)仍然表明缴费率与上解比例的最优组合关系还是反向变化关系。其三,国内研究(张军等,2003;白重恩和张琼,2014;彭浩然等,2018)[14-16]得出的资本产出弹性位于0.5至0.6区间,因此把资本产出弹性调整为0.55,数值拟合结果(图10)表明缴费率与上解比例最优组合在缴费率较低时仍然是反向变化关系。 图8 实际缴费工资基数检验图 图9 调整人口自然增长率检验图 图10 调整资本产出弹性检验图 在养老保险缴费率下调至24%的背景下,能否进一步下调养老保险缴费率以减轻企业负担并维持养老保险预算平衡是一个值得研究的问题。本文通过构建一个三部门跨期迭代模型研究了中央调剂制度下养老金替代率的影响因素,尤其是上解比例和缴费率两个因素,研究目的:一方面是分析养老金替代率的影响因素,另一方面是探讨在中央调剂制度下是否还具备下调养老保险缴费率的空间。 本文使用跨期迭代(OLG)模型研究了参保劳动人数与退休人数的人口因素、养老保险缴费率与上解比例的制度因素,以及利率与工资的经济因素是如何通过中央调剂制度影响养老金替代率的。研究发现:其一,上解比例越高,中央调剂金净流出省份养老保险预算平衡的养老金替代率越低,反之,中央调剂金净流入省份的养老金替代率越高。其二,在职参保劳动人口和离退休参保人口既能通过人口红利效应,又能通过中央调剂制度影响养老保险预算平衡的养老金替代率。其三,当政府养老保险预算平衡的养老金替代率等于市场出清的养老金替代率时,经济处于均衡状态。其四,养老保险缴费率与中央调剂制度上解比例的最优组合关系是两者之间的反向运动,也就是说如果政府下调养老保险缴费率,那么应该同时提高上解比例,这样就可兼顾政府养老保险预算平衡和市场出清。其五,在新冠肺炎疫情不利影响背景下,政府可通过消耗养老保险基金累计结余,实施暂时性下调养老保险缴费比例的措施,以缓解企业负担,从而实现“六保”中的保障居民就业目标。 为应对新冠肺炎疫情的不利影响,本文研究认为以规模庞大的基本养老保险基金累计结余为后盾,现阶段应该临时性下调养老保险缴费率,并且同时上调中央调剂金上解比例,这有助于减轻企业负担,促进居民就业。当新冠肺炎疫情消退之后再逐步恢复原来的养老保险缴费比例。研究不足之处在于构建理论模型过程中没有涉及养老保险基金累计结余和财政补贴问题,这有待今后进一步深入研究。三、养老金替代率影响因素的定性分析

(一)类型一的利率因素分析
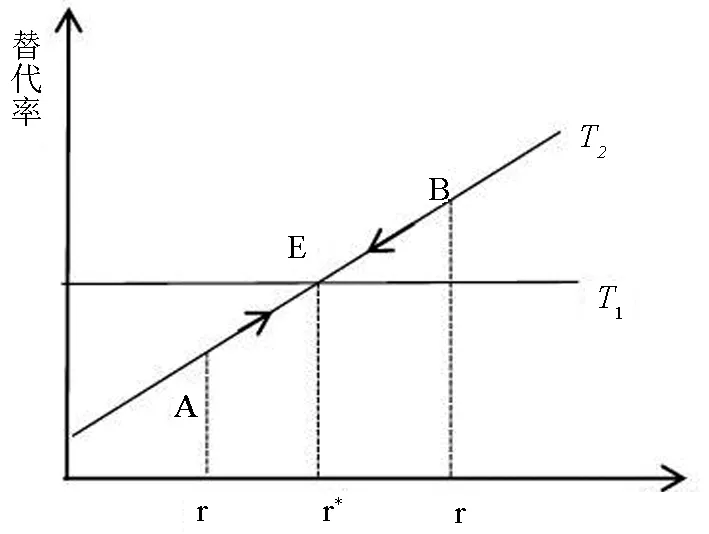
(二)类型一的上解比例因素分析
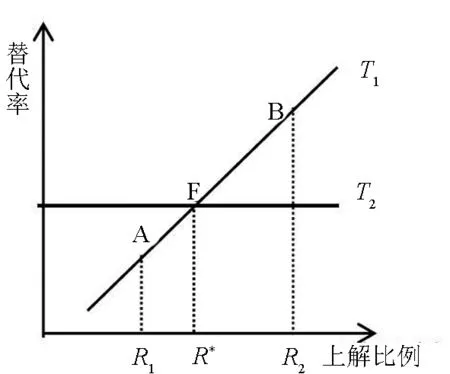
(三)影响类型二的参保劳动人口因素分析
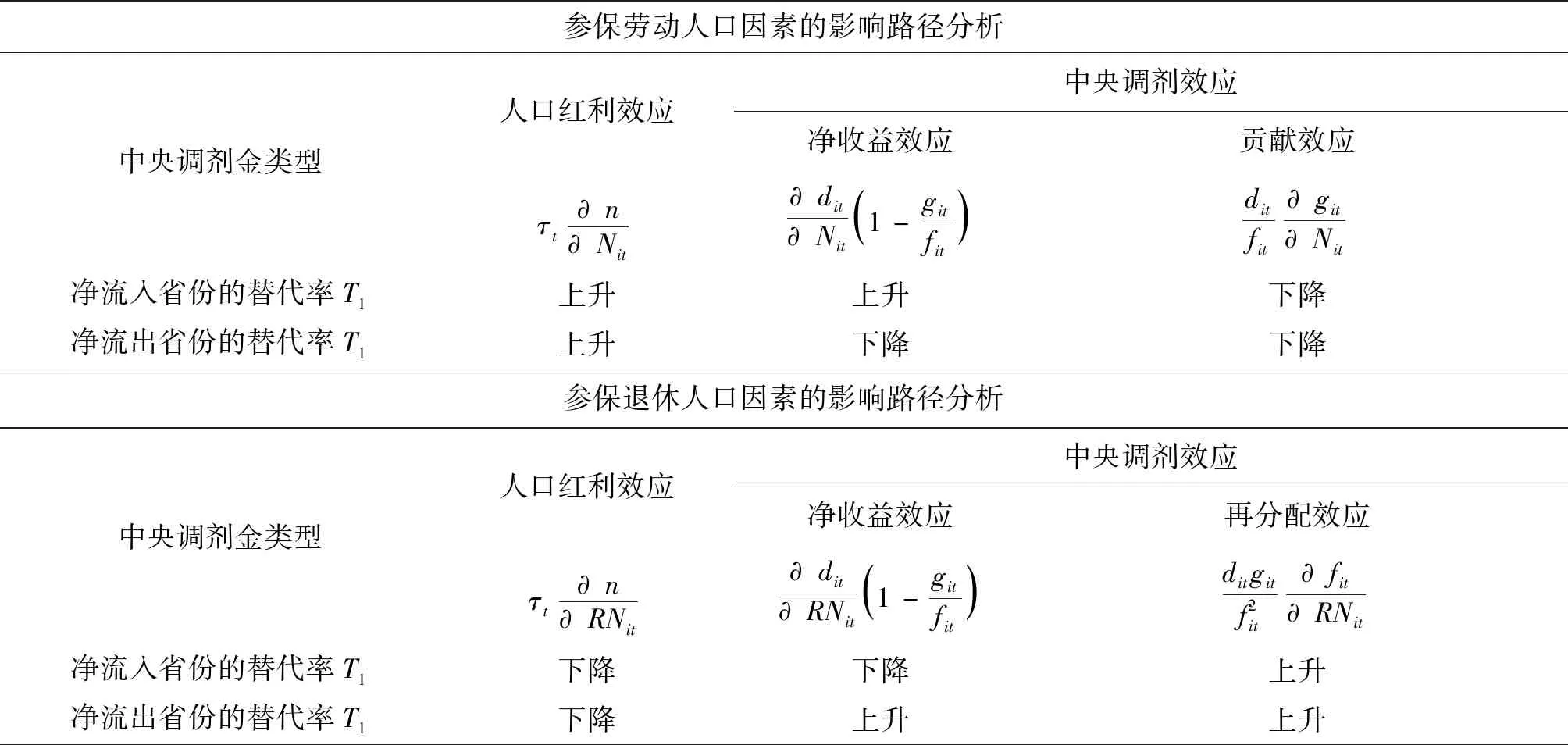
(四)影响类型二的参保退休人口因素分析
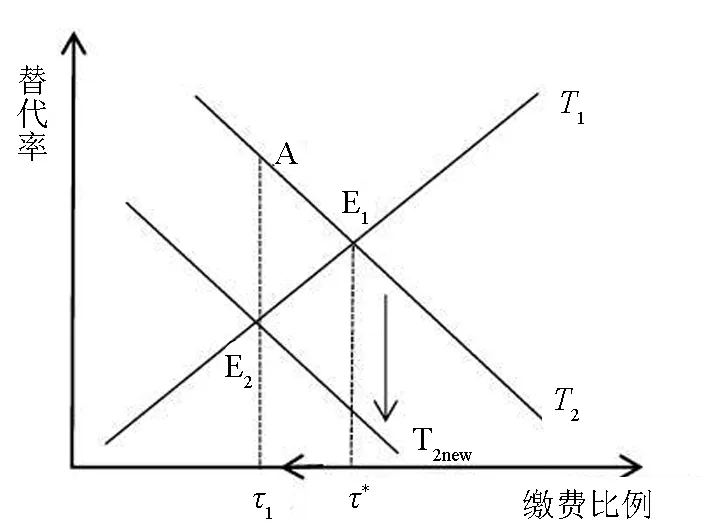
(五)影响类型二的养老保险缴费率因素分析
(六)影响类型二的工资因素分析
四、参数取值与数值模拟
(一)变量选取与参数取值

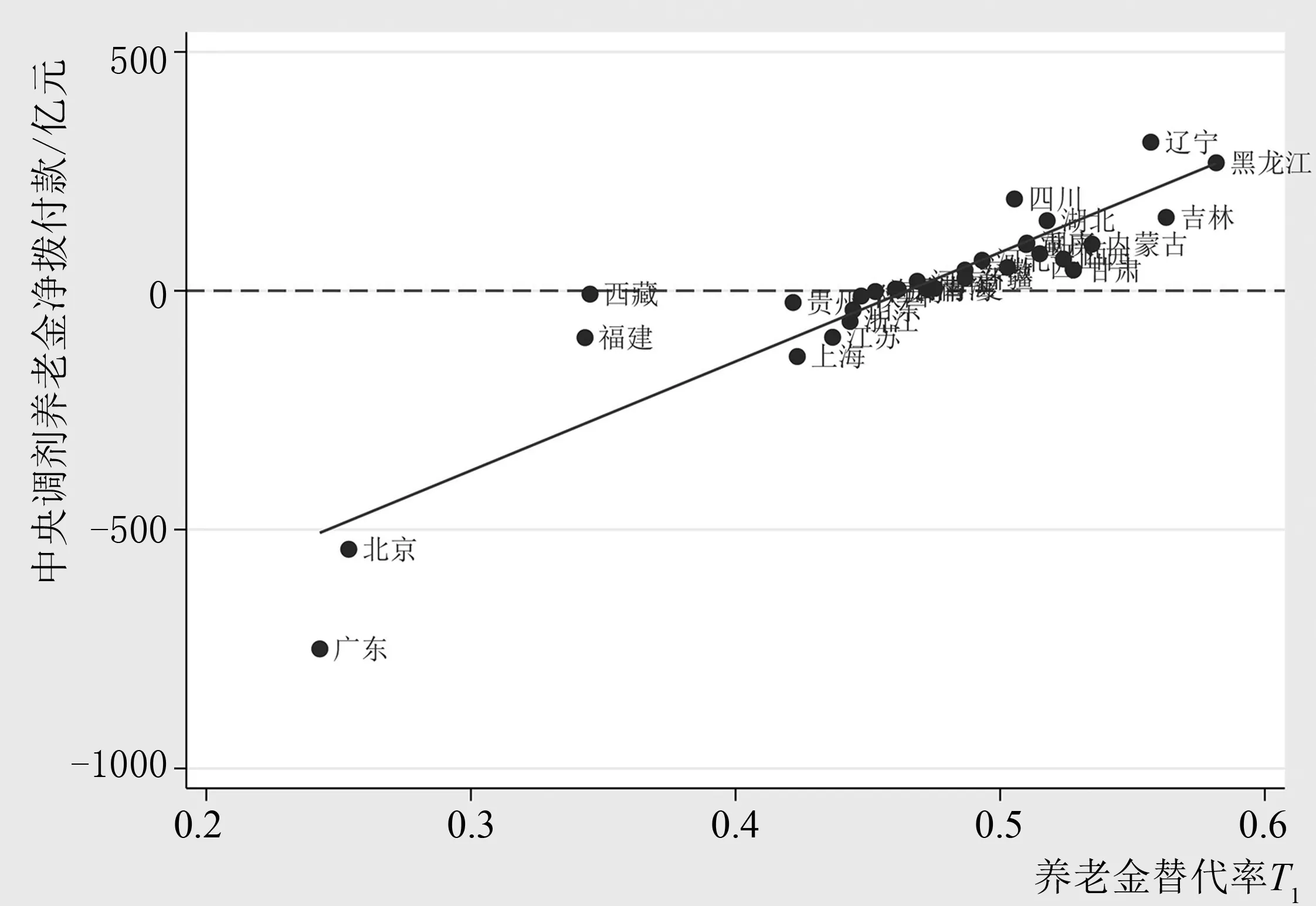
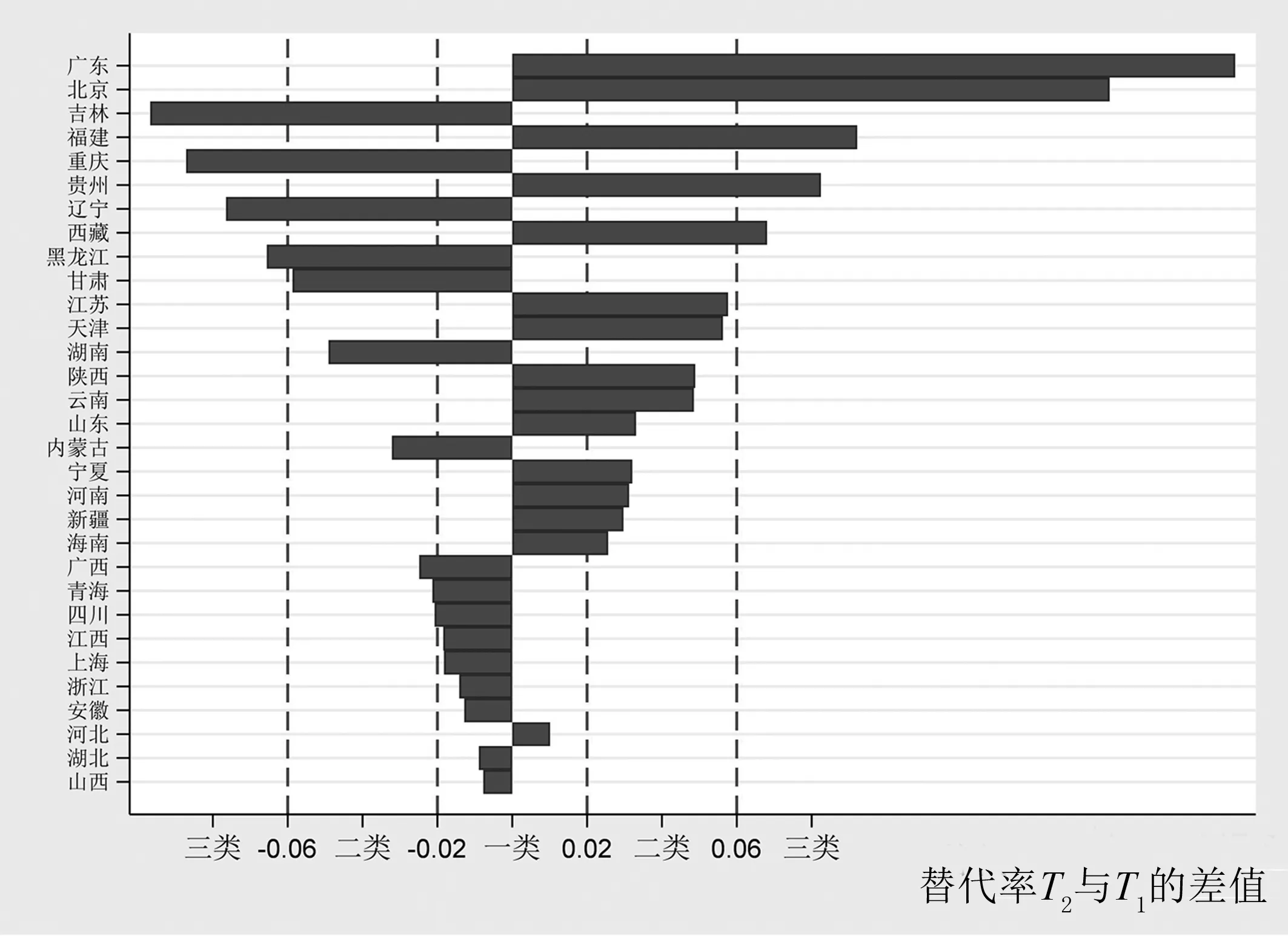
(二)养老金替代率T1和T2的实证结果分析

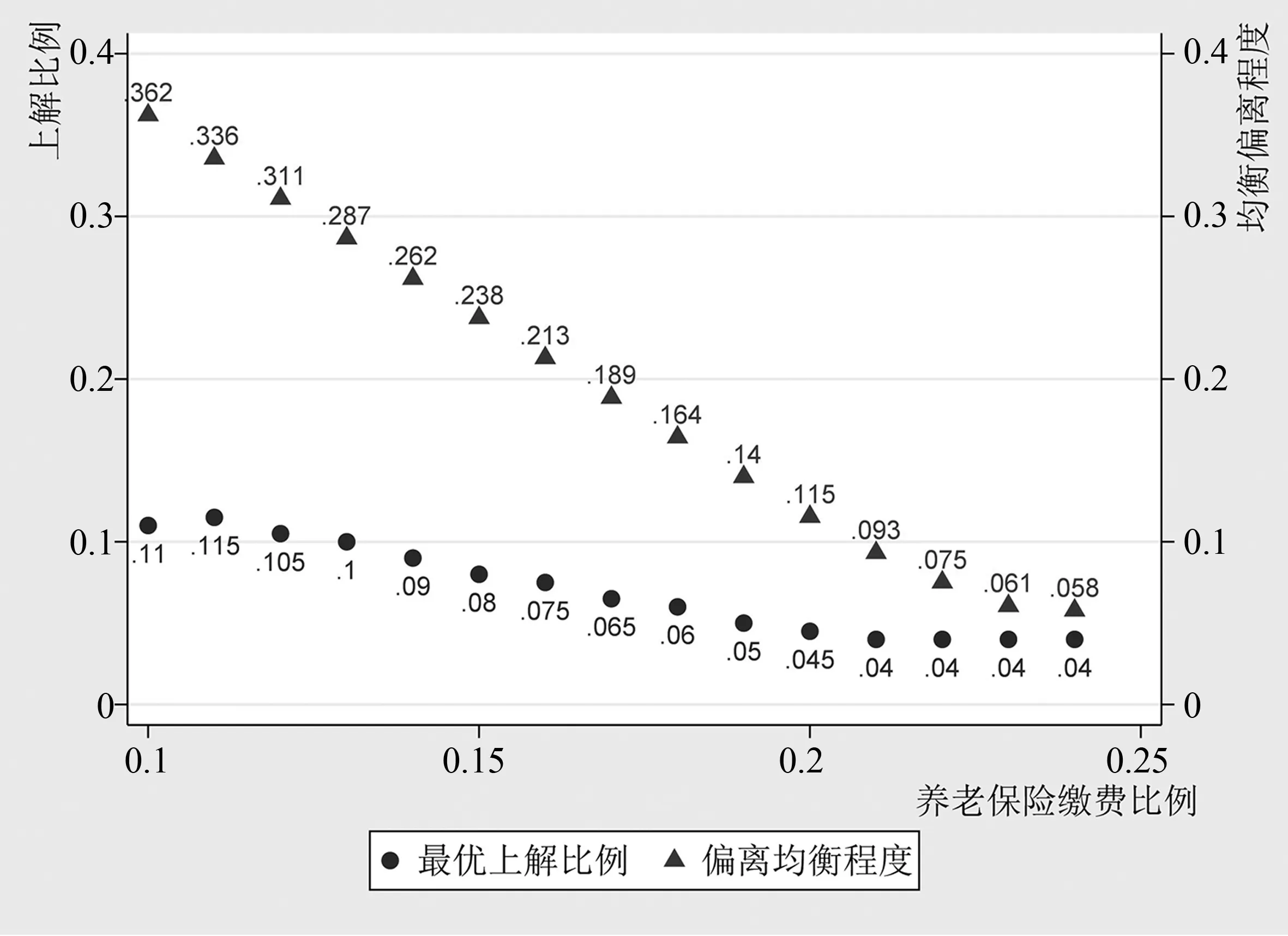
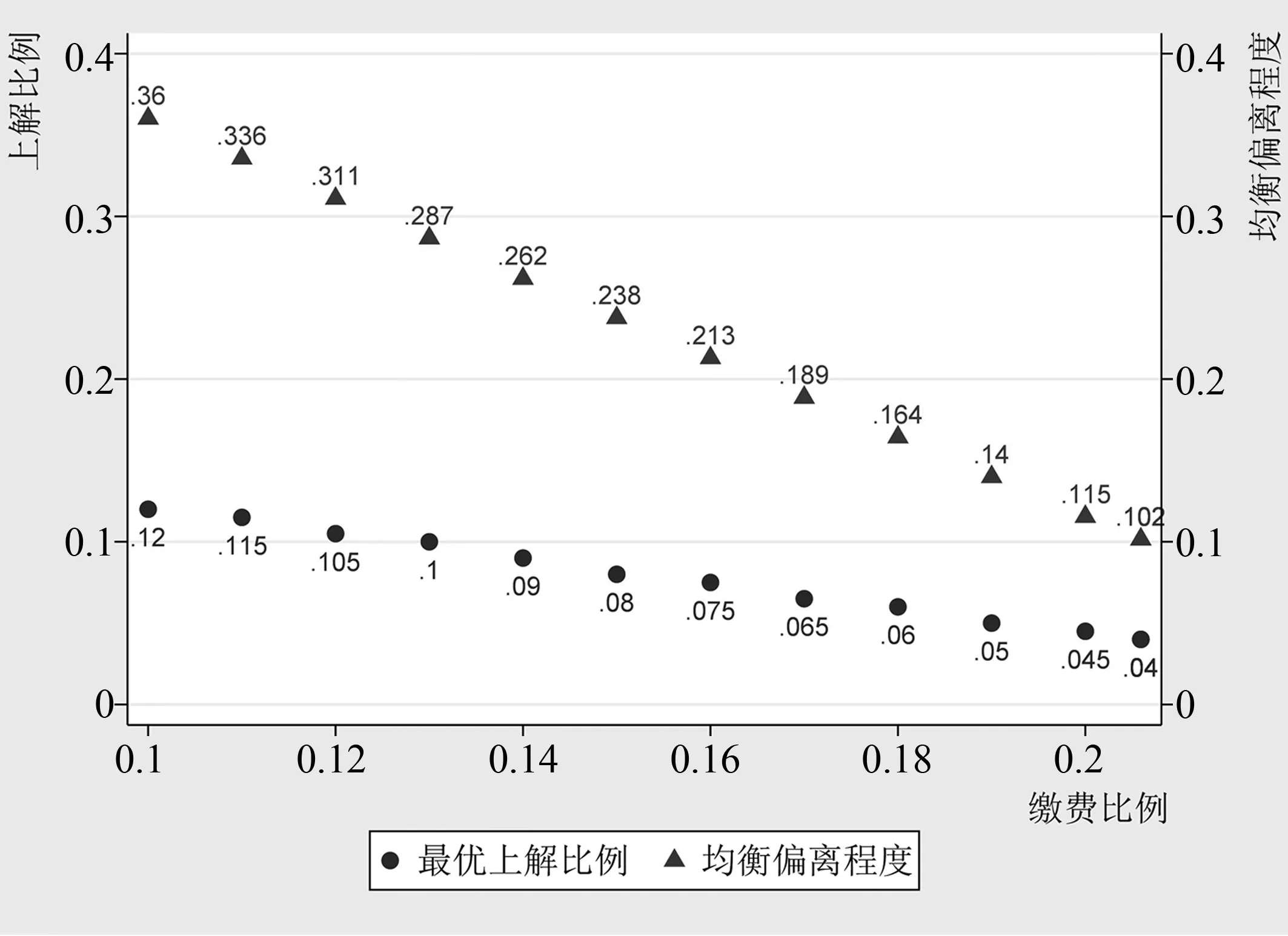
(三)数值模拟的缴费率与上解比例最优组合
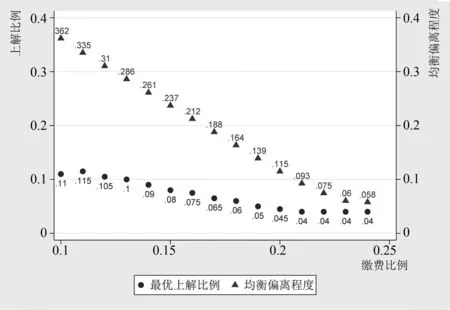
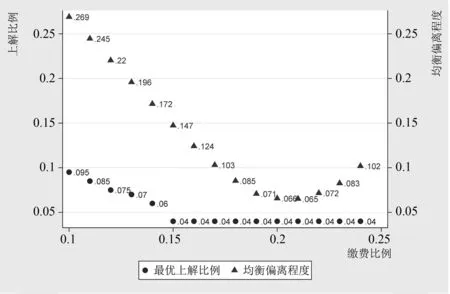
(四)最优组合稳健性检验
五、结论与建议
