基于GA-BP神经网络的航空铝合金预腐蚀疲劳寿命预测

魏雨晨，李旭东，刘治国，穆志韬

（海军航空大学青岛校区，青岛 266041）

引言

铝合金材料由于其成本低、强度高、密度小等优点，在现代飞机结构中被广泛使用。然而受高温、高湿、盐雾等气候环境的影响，服役于海洋环境下的飞机结构容易形成腐蚀损伤，结构的腐蚀损伤部位在疲劳载荷的作用下会使裂纹加速形成和扩展，从而使飞机结构发生疲劳破坏[1-4]。因此研究腐蚀损伤对航空铝合金疲劳寿命的影响对于保持现役飞机的可靠性和安全性、新研飞机的定寿延寿具有较大的工程价值。

由于腐蚀疲劳的内在机理十分复杂，结构的疲劳寿命受材料、环境、应力等多个方面的影响，所以可把腐蚀疲劳问题视为典型的多因素影响的非线性系统。BP神经网络作为当前应用广泛的智能算法，拥有很强的自我学习和非线性映射能力，很适合求解多元非线性问题。刘延利[5]基于预腐蚀疲劳试验数据利用BP神经网络建立了LY12CZ铝合金DFR值、点蚀深度与预腐蚀时间、温度之间的关系。纪冬梅[6]利用神经网络建立了介质浓度、应力比、频率与裂纹扩展速率系数C、m之间的关系，并结合Monte-Carlo法计算了压力容器腐蚀疲劳剩余寿命和可靠度。刘治国[7]利用牛顿插值法对原始试验数据进行扩充，利用神经网络建立了应力幅值和腐蚀年限与对数疲劳寿命之间的映射关系。然而由于神经网络算法本身存在一定的局限性，在实际应用的过程当中往往会出现训练时间较长、易收敛到局部最优等问题[8]。遗传算法作为一种广泛使用的优化算法，可优化神经网络的初始阈值和权值，其克服了神经网络算法本身的缺陷，对其预测精度及稳定性具有一定的提升效果[9-11]。

本文基于6A02铝合金试件实测蚀坑平均尺寸及其预腐蚀疲劳寿命试验数据，分别利用BP神经网络和GA-BP神经网络对6A02铝合金预腐蚀疲劳寿命进行预测，通过与测试集数据进行对比，利用误差分析比较两种模型的优劣性。

1 预腐蚀疲劳寿命试验

1.1 试验材料

试验材料为6A02铝合金，其为某型直升机动部件常用材料，原始试件形状和尺寸如图1所示，材料的主要力学性能及成分含量如表1、2所示。

表1 6A02铝合金主要力学性能

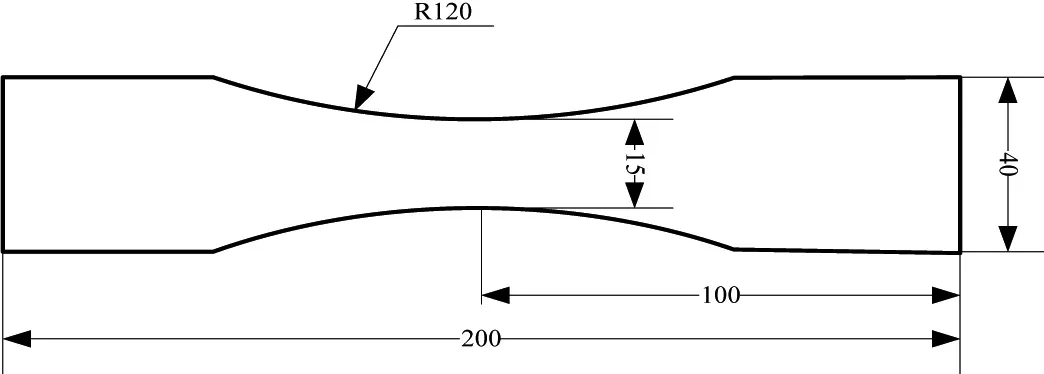
图1 试件尺寸形状

1.2 等级腐蚀试验

等级腐蚀试验以我国沿海驻屯机场气象环境数据为依据，利用统计、折算等方法编制地面停放环境谱，再通过试验室人工环境与机场服役环境的腐蚀当量关系，编制加速腐蚀环境谱[12-14]，如图2所示，飞机在外场服役一年所受腐蚀损伤等效于试验室加速腐蚀255个循环。

表2 6A02铝合金成分含量(%)

图2 铝合金加速腐蚀环境谱

参照文献[15]的方法，基于腐蚀等级评价标准评定加速腐蚀后试件的腐蚀等级。具体操作方法为：在进行加速腐蚀试验时，每经过一定的腐蚀时间，随机取出一定数量的试件，利用KH-7700显微镜测量试件表面蚀坑尺寸参数及孔蚀率，计算相应的腐蚀等级，若达到规定等级，则取出满足要求的试验件，若未达到，则继续进行试验。图3为不同腐蚀等级下试件的局部腐蚀形貌。

图3 不同腐蚀等级下试件的局部腐蚀形貌

1.3 疲劳寿命试验

依据《金属轴向疲劳试验方法》中的规定方法，测定试件在不同腐蚀等级不同应力水平下的疲劳寿命。试验采用QBG-100型疲劳试验机，试验环境为大气室温，波形为正弦，加载频率f=100～125 Hz，应力比 R=0.1。进行试验时，每个腐蚀等级先选取一个试件做载荷调试和静力标定，之后再按照成组法测定试件在不同应力水平下的疲劳寿命。

2 建立BP神经网络模型

2.1 样本数据

以试件表面实测蚀坑平均深度、宽度、面积和最大应力作为输入，以对数疲劳寿命作为输出，构建神经网络建立预腐蚀疲劳寿命预测模型。预腐蚀疲劳试验数据共44组，各个腐蚀等级各个应力水平随机选取一组共9组数据作为测试集数据（见表3），其余35组数据作为训练集数据用于模型训练。

表3 测试集数据

2.2 网络结构及参数设置

许多理论研究表明，3层神经网络结构能够较好地描述任何非线性关系[16]，故网络结构为4-H-1三层，即输入、隐含、输出层节点个数分别为4、H、1，隐含层节点数H可由如下经验公式[17]进行计算：

式中：

H、a、b—隐含、输入、输出层节点个数；

c—1～10之间的任意常数。

通过（1）式可以计算出H的初始取值范围为[4，13]。

在初始取值范围内，不断改变隐含层节点数H的取值，当H=11时，神经网络训练的均方误差最小，故隐含层节点数取11。

利用Matlab编程建立神经网络模型，在开始训练网络前，首先将所有输入、输出数据进行归一化，以消除数据数量级之间的差别对预测结果的影响，在网络训练结束后，再将输出数据反归一化以得到实际值。网络隐含层选取tansig作为激励函数，输出层选取purelin作为激励函数，整个网络选取traingdx作为训练函数。为保证模型的训练精度，并防止网络出现过拟合现象，经过不断尝试，最终确定网络的最大训练次数为1 000，学习速率为0.01，目标误差为0.01。

3 遗传算法（GA）优化BP神经网络

由于神经网络的初始阈值和权值为随机选取，不合理的阈值和权值往往会使网络出现学习效率较低、收敛到局部最优等问题。为解决以上问题，可利用遗传算法对神经网络进行优化，以使优化后的神经网络拥有更好的预测性能，算法基本流程如图4所示，具体步骤为：

图4 GA-BP神经网络算法流程图

1） 对种群中的个体进行编码。用实数对个体进行编码，个体由网络阈值和权值两部分构成，由于本文的神经网络结构为4-11-1型，所以阈值个数为11+1=12个，权值个数为4×11+11×1=55个，总编码长度为67。

2）确定优化目标函数。将网络训练均方差作为优化目标函数F，其计算公式为：

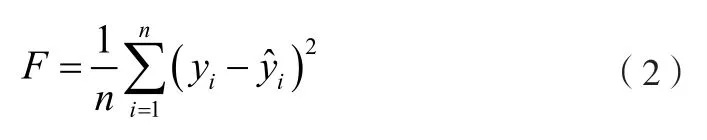
式中：

n—训练样本个数；—预测输出；yi—实际输出。

3） 选择操作。以个体本身的适应度大小作为选择依据，从种群中选择适应度好的个体构成新种群，以便于后续个体的交叉和变异，第i个个体被选中的概率pi为：

式中：

fi—第i个个体的适应度；

Fi—第i个个体的均方差；

k—转换系数，N—种群中的个体总数。由于均方差Fi越小越好，所以在选择个体时适应度fi取均方差Fi的倒数。

4）交叉操作。两个个体以一定概率互换其部分基因，以形成新个体。个体ak和个体al交换其第j位基因的方法如下所示：

式中：

b—[0,1]之间的随机数。

1、学生文化基础薄弱，学习意识不强。目前，中职学校的生源来自于中考失利甚至是未参加中考的学生，也有辍学后重回学校的社会人员。因此，学生文化基础课普遍较差，对全新的专业基础和技能课，更是无从下手。

5）变异操作。部分个体的部分基因以一定的概率发生变异以使种群多样化。

6）重复步骤3）～5），直到达到最大遗传代数。

7）对优化个体解码得到网络优化后的阈值和权值，将优化的阈值和权值赋给神经网络并对网络进行训练。

8）利用测试集数据检验优化后模型的预测精度。

4 预测结果及误差分析

为验证遗传算法对BP神经网络的优化效果，将GA-BP神经网络和传统BP神经网络两种模型的预测结果进行对比，结果如图5、6和表4所示。

表4 GA-BP和传统BP神经网络预测性能比较

从图5可以看出，随着进化代数的增加，GA-BP神经网络的预测均方差在不断减小，说明模型的预测性能在不断提升，经过50次进化后，模型的预测性能达到最佳。

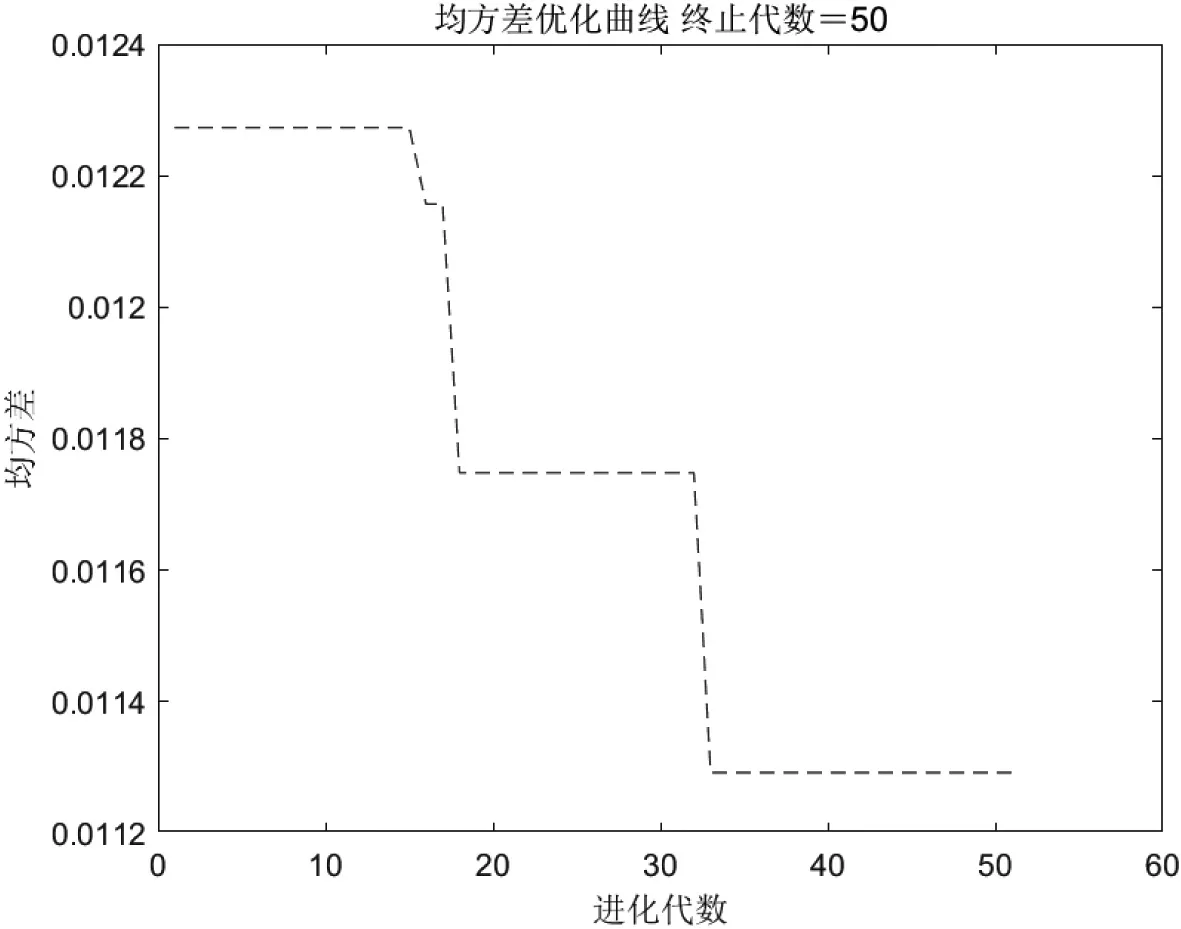
图5 GA-BP神经网络均方差优化曲线

图6 GA-BP和传统BP神经网络预测结果比较

通过对表4数据的进一步对比可以看出，GA-BP神经网络的预测相对误差均值和方差均低于传统BP神经网络，其预测精度和稳定性更高，这表明遗传算法对传统BP神经网络的预测性能具有一定的优化效果。

5 结论

1）通过等级腐蚀试验和预腐蚀疲劳寿命试验获得了试件表面实测蚀坑平均尺寸及其疲劳寿命数据，以试验数据为样本，分别利用BP神经网络和GA-BP神经网络建立了6A02铝合金预腐蚀疲劳寿命预测模型，将模型预测结果与测试集数据进行对比发现，两种模型的预测效果较好，相对误差均在10 %以内。

2）相对于传统BP神经网络模型，GA-BP神经网络模型的泛化能力和预测精度更高，其更适合用于预测6A02铝合金预腐蚀疲劳寿命，可为其实际工程应用提供参考。