强对流环境下输电塔线体系的振动耦合响应与可靠性分析
2022-11-25陈科技康丽莉张琳琳陈赛慧
陈科技,康丽莉,张琳琳,陈赛慧
(1.电力经济技术研究院 国网浙江省电力有限公,杭州 310014;2.浙江省气象科学研究所,杭州 310008)
引言
随着经济水平和环保意识的不断上升,国家东南沿海地区对电能的需求不断上升。然而,东南沿海地区在快速建设电网系统的同时,也同样面临着恶劣天气环境给输电塔线所带来的严峻挑战[1]。输电塔线的安全运行和稳定维护是各个行业领域快速稳定发展的前提,然而在面对高强度、高湍流和强脉动的强对流大风天气时,输电塔线往往会受到毁灭性的打击[2,3]。例如,浙江省在2007年遭受“韦帕”侵袭,约150 km的输电线路出现倒塔断杆;浙江省温州市在2006年遭受“桑美”侵袭,一万多基输电线路受损严重……
对于强对流大风高湍流、强脉动、多阵风、强度大等特性,仅仅使用“最大风”校验方法对输电塔线进行抗风设计是远远不够的。同时,强对流环境的数据采集、状态监测等工作很难开展,且数据获取精度较低[4-6]。因此,通过反演强对流环境参数,分析输电塔线体系结构性能,对于提高输电线路的安全性和对恶劣天气的抵抗能力,为浙江省及其他沿海地区输电塔线体系的抗风设计提供技术支撑具有重要意义。
为对浙江省及其他沿海地区输电塔线体系的抗风设计提供技术支撑,本文构建“一塔两线”有限元模型,模拟了强对流环境下的脉动风场,基于有限元时程分析和脉动风载荷计算方法,分析了强对流环境下输电塔线体系的振动耦合特性,评估了输电塔线体系的可靠性。首先,基于脉动风载荷研究输电塔主材轴力的时空分布规律,研究强对流脉动风载荷的脉动放大作用;然后,分析强对流环境下导地线的线条风载荷对主材轴力的影响作用;最后,考虑了脉动放大作用后,研究了输电塔主材构件的受压强度和稳定性。
1 输电塔线体系有限元建模
本文选取浙江省舟山市的一处猫头塔(塔高26.5 m,档距250 m)进行强对流环境下输电塔线体系振动耦合响应,该塔结构为“一塔两线”。采用Beam188单元、Link8单元和Link10单元分别模拟输电塔主材、绝缘子串和导线;采用V型找形法选取导线和地线的几何形态,直至应力和弧垂符合误差需求;设定塔线体系边界条件,全约束塔腿四个节点、平动约束X/Y/Z三个方向,最终建立一塔两线的110 kV猫头塔有限元模型(图1),并且在输电塔关键节点进行标记(图2),以分析振动耦合响应分析。

图1 猫头塔有限元模型

图2 塔身关键单元标记图
2 强对流环境脉动风场模拟
1)湍流强度
强对流环境下的脉动风湍流强度决定了风载荷的脉动强度。定义某一高度Z处10 min内的平均风速为Uz,且该处风速标准差为σz,湍流强度[7]为:

然而,该式并不适用于所有地形地貌,因此本文在综合考虑了气象实测、高度变化、地形地貌之后,定义地面粗糙度指数α,距地高度Z=10 m,并取峰值系数g为2.2,则:
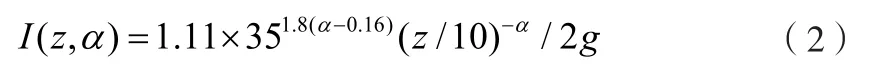
2)脉动风速功率密度谱
对于功率密度[8],本文在此定义10 m处的脉动风功率谱为 Sv,(m2/s);x= 1200n/;该处平均风速为,(m/s);频率为f,(Hz);粗糙度长度为k;则:
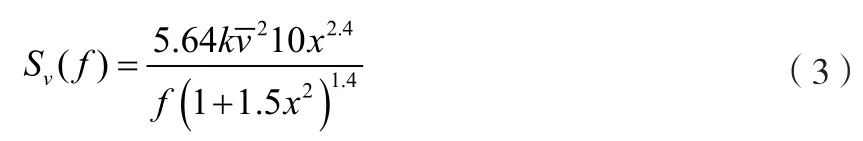
3)脉动风谱求解
本文选用自回归(AR)线性滤波法[9,10]对随机振动和时序变化的脉动风进行风谱求解。本文在此定义X= [x1,… ,xM]T,Y= [y1,… ,yM]T,Z= [z1, … ,zM]T;自回归模型AR阶数为p,其M×M阶方阵为Ψk;1≤k≤p;时间步长为Δt;而N(t)作为独立随机过程向量。因此,脉动风速时程V(X,Y,Z,t)为:

从上式可知,Ψk和N(t)为后续主要解决的重点。
1)求解Ψ
在此定义随机性较强的自相关矩阵为(p+ 1 )M· (p+ 1)M阶的协方差R;Ψ 为(p+1)M·M阶矩阵阶方差矩阵为RN;M阶单位阵为I;pM·M阶零矩阵为Op。因此,R和Ψ之间关系为:

其中,协方差R为:

在此定义,i,j= 1,2,…p+ 1 ;m= 1,2,…p,协方差矩阵R中的M·M阶矩阵Rij(mΔt)可表示为:
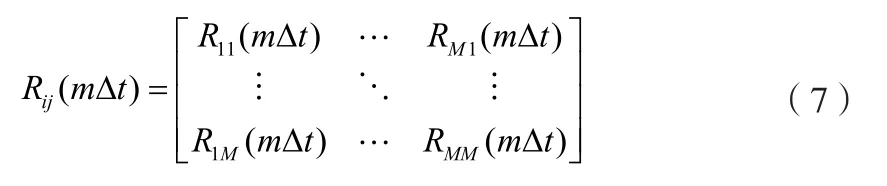
在此令τ=mΔt,则上式可转化为:
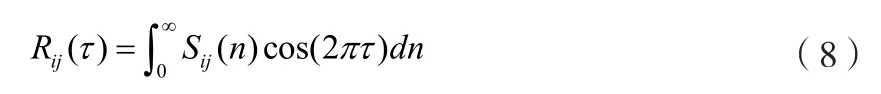
从上式可以看出,rij(n)为相关系数;当i=j时,Sij(n)为自功率谱函数;当i≠j时,Sij(n)为互功率谱函数。此时,由可得为求解N(t)提供条件。
2)求解N(t)
N(t) =L·n(t),RN=L·LT
3)求解脉动风速
经过1)Ψ和2)RN的求解,将脉动风速时程V(X,Y,Z,t)进行M个空间的时间离散化,定义Δt为时间步长,当t<0时,ui(t) = 0,则:
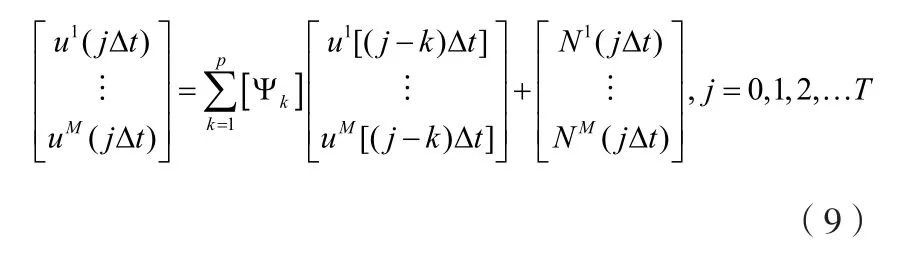
4)求解最终风速
由前文平均风速和3)脉动风速共同组成实际风速。除平均风速之外,在此定义基准高度和计算高度分别为z0和z,可根据不同高度处的风剖面指数率α进行换算,则最终风速表示为:

4)强对流脉动风模拟
本文对浙江省舟山市的一塔两线猫头塔进行分段简化。采用距地10 m的基准风速v10=31.5 m/s(15年重现期风速);风剖面指数α=0.12(A类地貌);时间步长Δt=0.25 s;粗糙度长度k=0.1 m。本文对猫头塔模型进行不同输电塔高度节点下的强对流脉动风进行模拟,结果如图3所示。
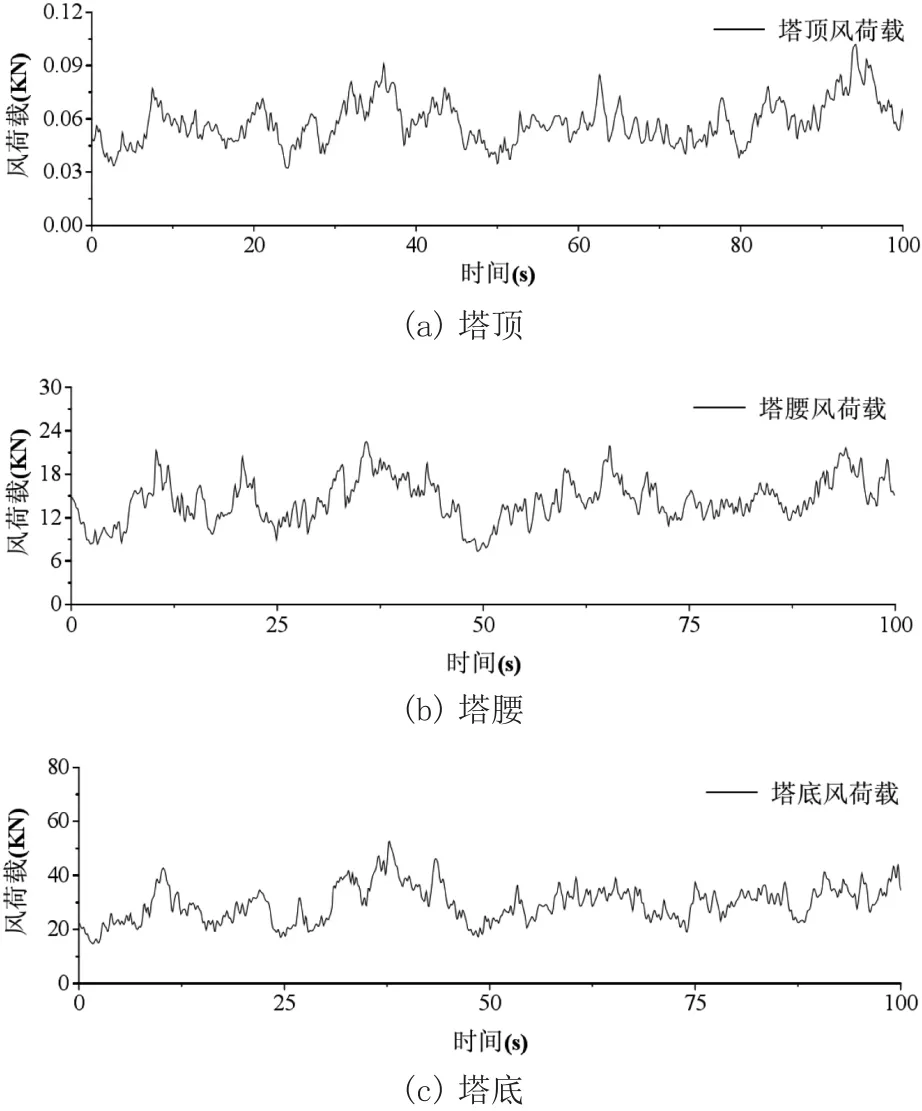
图3 强对流脉动风荷载时程曲线
3 强对流输电塔线体系振动耦合响应分析
3.1 有限元时程分析
1)系统运动微分方程
采用系统运动微分方程描述脉动风载荷下的输电塔线体系[11]。在此定义,施加脉动风载荷{F(t)}下,输电塔线的质量矩阵、阻尼矩阵和刚度矩阵分别为[M]、[C]和[K];某时刻t下任意节点的加速度、速度和位移分别为则系统运动微分方程表示为:
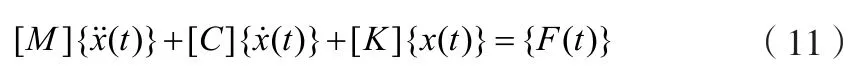
同时,由于脉动风载荷下的输电塔线体系会出现不同程度的结构形变,因此本文选用直接积分法对强对流下输电塔线体系进行振动耦合响应分析。
(2)系统运动微分方程求解
本文采用隐式逐步积分算法——New Mark法进行振动耦合响应分析[12]。对上式的非线性因素加以考虑,定义位移的非线性函数——弹力分量{F(t+Δt)},则上式转化为:

同时,(t+Δt)时刻的位移分量为Δx(t+ Δt) =x(t+ Δt)-x(t);对{F(t+Δt)}和[KT{x(t)}]引入切线刚度矩阵,则:

加入某时刻t的运动平衡方程:
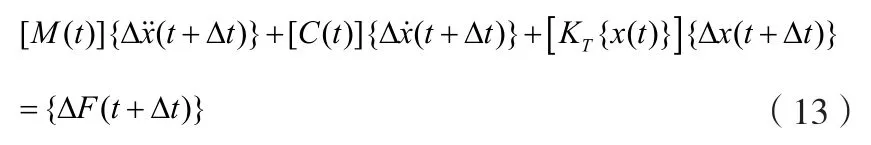
其中:
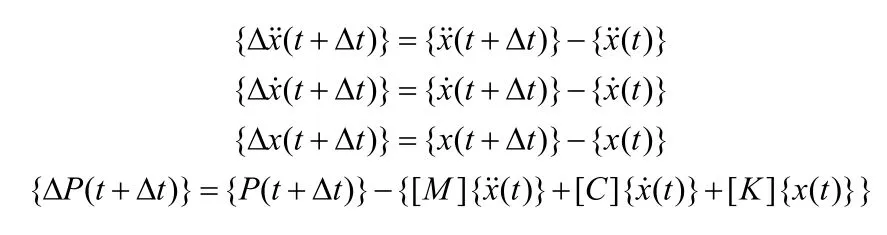
{ΔP(t+ Δt)}表示保持系统平衡的载荷增量,在任意时刻所得残余应力均输入下一迭代计算。定义任意迭代次数i时的加速度、速度和位移增量分别为(t+ Δt)、
(t+ Δt)和δxi+1(t+ Δt),则迭代求解为:

其中:
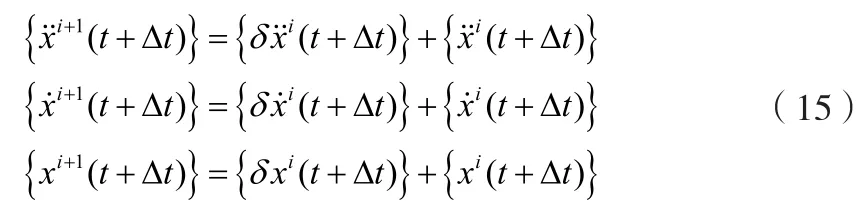
3.2 风载荷计算
对地导线和塔身结构的脉动风载荷分别进行计算[11,12]。在此定义,基本风压W0;风压不均匀系数αf=0.85,风压高度变化系数μsc=1.1(导线)和1.2(地线);脉动风载荷调整系数βc=1.15(插值);风向与导线夹角θ=90 °。同时,d、L和A分别为导线直径、长度和塔身投影面积。则:
地导线:PD=αf·W0·μz·μsc·βz·d·L·sin2θ
塔身结构:PT=μz·μsc·βz·A·W0
3.3 振动耦合响应分析
为对浙江省及其他沿海地区输电塔线体系的抗风设计提供技术支撑,本文在此首先基于脉动风载荷研究主材轴力的时空分布规律;然后计算强对流环境下线条风对主材轴力的影响作用;最后分析输电塔身主材在强对流脉动风下的结构稳定性和倒塔原因。
3.3.1 主材轴力分布
本文选取图2中的单元1、单元5和单元21作为塔身主材迎风面的轴力时程变化曲线(图4(a));选取图2中的单元2、单元6和单元22作为塔身主材背风面的轴力时程变化曲线(图4(b)),时间间隔均为10 s。从图4可以看出,无论是塔身主材的迎风面和背风面,强对流脉动风载荷下的轴力随时间变化趋势相同,均在同一时刻出现轴力峰值;并且随着塔身节点的高度越高,塔身主材的压力越小,轴力与塔身节点高度呈正相关变化趋势。同时,从迎风面和背风面的轴力数值正负号可知,塔身主材在迎风面受到拉伸作用力,在背风面受到挤压作用力,这也验证了90 °强对流风载荷下的力矩作用效果大于重力载荷。

图4 主材轴力时程曲线
图5为静风和强对流脉动风载荷下的塔身主材轴力在高度方向上的变化规律图。从塔身主材在背风面(图5(a))和迎风面(图5(b))的轴力变化图可以看出,塔身主材在迎风面受到拉伸作用力,在背风面受到挤压作用力。同时,强对流脉动风载荷下的主材轴力极值远大于静风载荷,这是因为静风载荷下的调整系数根据良态风脉动放大而来,而一旦涉及到湍流强度大的强对流环境,其风载荷的脉动作用会加大,造成了塔身结构受损的概率和程度。
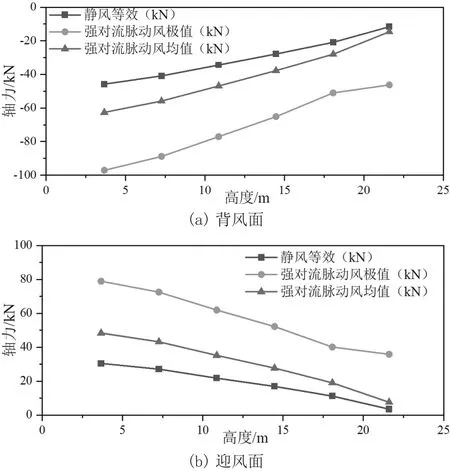
图5 轴力极值变化规律
3.3.2 线条风对主材轴力贡献率
由于绝大多数输电塔线体系的档距跨度大,因此实际强对流环境中的导线和地线承载了不可忽视的线条风载荷。因此,本文在此选择图2中的单元2作为线条风载荷对主材轴力贡献率的研究对象。同时,由于单元2在背风面,本文采用截面法构建输电塔线的背风面受力简图(图6)。
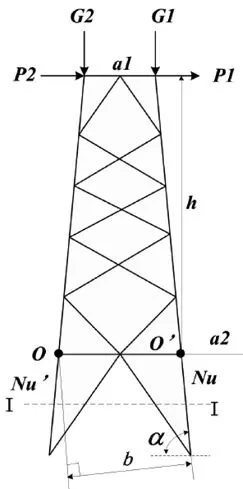
图6 输电塔线背风面主材受力简图
在此假设输电塔重力为G,简化得到塔身上端的简化重力G1和有限元计算得到迎风面风载荷P1和背风面风载荷P2,均由绝缘子串处的X方向力FX计算得到;MSW表示塔身风载荷对截面I-I的作用力矩;a1和a2分别表示塔身横隔面宽度和第一个横隔面的宽度;绝缘子串与a2之间的高度差为h;风载荷导致的塔身倾斜角度为α;以O点取矩时的作用力臂用b表示。
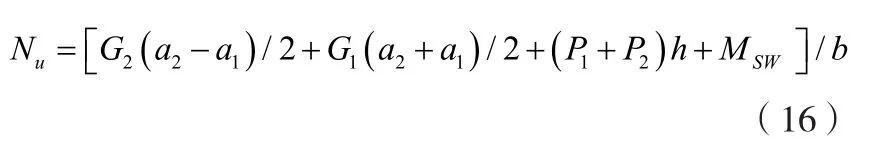
图7为绝缘子串处沿X方向作用力的时间分布曲线,即为导线和地线随着时间变化在X方向上的受力分布曲线。分析图7可知,强对流脉动风条件下的导线比地线承担了更多由风载荷的传递力量,这是因为导线直径大于地线直径。
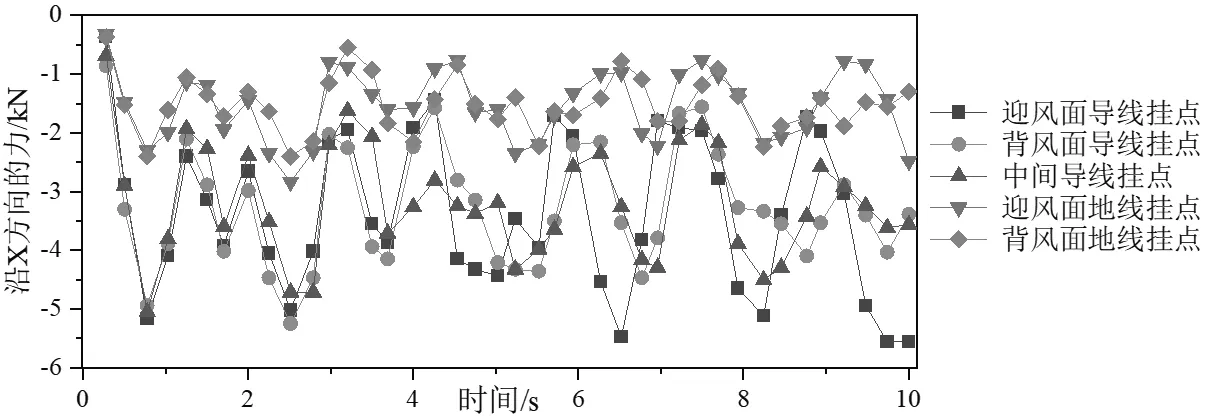
图7 绝缘子串处沿X方向作用力的时间分布曲线
图8(a)为静风和强对流脉动风下,不同风载荷模式下O′点的作用力矩;图8(b)为静风和强对流脉动风下,单元2在有无线条风载荷条件下的轴力和贡献率。分析图8可知,在考虑线条风载荷的情况下,强对流脉动风对单元2造成了较大的影响,极值状态下的线条风贡献率高达60.02 %。因此,在考虑抗风防风的设计中,需要充分考虑强对流环境下输电塔线的线条风载荷,可以采取“落线护塔”的方式降低塔身结构的受力效果。同时,由于线条风载荷与档距之间呈正相关关系,还可以通过减小输电塔线体系的档距作为强对流环境下的保护措施。

图8 不同风载荷模式下线条风的主材轴力及贡献率
3.3.3 主材受压构件的强度分析
分析主材轴力时程分析结果可知,塔身主材在背风面受到挤压作用力。因此,本文选取背风面的单元2、单元6和单元22,利用输电塔线挤压稳定计算公式对主材构件的受压稳定性和受压强度进行校验。同时,本文还计算了静风载荷下的主材构件临界载荷,以研究强对流脉动风的脉动放大作用。考虑到不同部位的塔身主材构件具有较大的受力差异,特别是在同一水平截面的背风面和迎风面主材具有更大的轴力差异。因此本文对单元2、单元6和单元22的构建参数置于表1中。

表1 构件参数表
在此定义抗压强度设计值为f,MPa;受压构件设计值为N,N;构件横截面积为A,mm2;受压稳定系数φ;稳定强度折减系数为mN=1.0;角钢尺寸得:

可得挤压稳定计算公式:

同时,在此定义脉动放大比为强对流脉动风载荷轴力极值与15年重现期静风载荷轴力极值的比值。通过将静风载荷轴力极值、强对流脉动风载荷轴力极值和上式计算所得的挤压轴力设计值进行对比,最终计算结果如图9所示。在不考虑强对流脉动风载荷时,静风载荷极值均明显低于挤压轴力设计值,而在考虑脉动放大作用之后,施加了强对流脉动风载荷后的主材轴力极值均明显高于设计值,单元2、单元6和单元22的脉动放大比均在2倍以上。这也正确解释了输电塔线体系的倒塌事故:强对流环境下,输电塔线体系会在强对流脉动风的放大作用下,造成输电塔受压失稳、进而破坏折损。

图9 构件轴向压力极值和设计值
4 结论
为对浙江省及其他沿海地区输电塔线体系的抗风设计提供技术支撑,以2021年浙江省舟山市一处110kV猫头塔倒塔事故为研究背景,本文构建“一塔两线”有限元模型,模拟了强对流环境脉动风场,基于有限元时程分析和脉动风载荷计算方法,分析了强对流环境下输电塔线体系的振动耦合特性,评估了输电塔线体系的可靠性。
首先,基于脉动风载荷研究了输电塔主材轴力的时空分布规律,研究了强对流脉动风载荷的脉动放大作用;然后,以背风面构件单元2为研究对象,分析了强对流环境下导地线的线条风载荷对主材轴力的影响作用,强对流脉动风的线条风载荷贡献率最高可达60.02 %;最后,研究了单元2、单元6和单元22的受压强度和稳定性,考虑了脉动放大作用后,强对流脉动风的脉动放大比已经超过了2倍。这也是输电塔身主材在强对流脉动风下的结构稳定性和倒塔原因,主材会在强对流脉动风的放大作用下受压失稳,进而折损倒塔。
