高速铁路矮塔斜拉桥运营阶段收缩徐变效应分析
2022-11-25胡豪施洲
胡 豪 施 洲
(1.中铁工程设计咨询集团有限公司,北京 100055;2.西南交通大学土木工程学院,成都 610031)
引言
混凝土收缩徐变会影响大跨度预应力混凝土梁桥的内力和变形状态,从而影响行车性能,高速铁路桥梁上这种影响尤为明显[1-3]。预应力混凝土矮塔斜拉桥作为一种典型的大跨度预应力混凝土梁桥,近年来在高速铁路上应用较多,且多采用无砟轨道,其收缩徐变效应问题对结构影响较大[4-6]。
胡狄等通过试验分析多种因素对预应力混凝土梁桥收缩徐变的影响,并提出考虑配筋影响的收缩徐变计算方法[7];乔健等对三座不同结构形式的铁路大跨度预应力混凝土梁桥受力和变形的影响进行分析[8],提出控制梁部上下缘恒载应力水平接近等措施;薛宇光比较几种常用收缩徐变计算模型的优缺点,然后选取不同收缩徐变计算模型分析某铁路大跨度预应力混凝土梁桥的收缩徐变效应[9];李恩良比较不同规范中规定的收缩徐变计算模型,认为铁路规范中收缩徐变计算模型偏保守[10-11];曾庆响应用数值模拟的方法研究了不同收缩徐变模型对大跨度预应力混凝土箱梁桥的受力和变形影响差异,并定量分析了龄期、环境湿度、混凝土强度等因素对混凝土收缩系数和徐变系数的影响规律[12];王琦等分别针对不同的高速铁路矮塔斜拉桥,研究了收缩徐变对结构工后变形的影响和控制措施[13-14];张欣欣等针对池黄高铁太平湖特大桥主桥,探究三塔矮塔斜拉桥斜拉索二次张拉技术对收缩徐变效应的影响[15-16];卢明辉等研究收缩徐变效应对高铁大跨矮塔斜拉桥施工控制过程中的影响[17-18]。
目前,对高速铁路预应力混凝土矮塔斜拉桥的收缩徐变问题研究,主要集中在收缩徐变的计算方法、收缩徐变对结构后期变形和施工控制过程中的线形控制的影响等方面,针对其运营阶段收缩徐变效应规律分析的研究相对较少。
预应力混凝土矮塔斜拉桥的收缩徐变效应相对复杂,后期结构变形控制难度较大,且高速铁路无砟轨道桥梁运营期间的变形要求高。因此,设计阶段应重视结构运营阶段收缩徐变效应分析。以新建京沈高铁潮白河特大桥主桥为例[19],借助有限元方法,详细分析收缩徐变对结构变形和受力的影响规律,以期为后续同类桥梁结构的设计研究提供参考。
1 工程概况
北京—沈阳高速铁路设计速度300 km/h,上跨怀河和京承高速公路时,采用跨度为(65+85+178+93)m的预应力混凝土矮塔斜拉桥,桥上铺设CRST Ⅲ型板式无砟轨道,主桥总体布置见图1。采用塔梁固结、梁墩分离的连续梁体系,141号墩顶设置纵向固定支座,其余墩顶设置纵向活动支座。141号、142号墩与主梁间各设置4套黏滞阻尼器,以提高主桥的抗震安全性。

图1 主桥总体布置(单位:m)
主梁为预应力混凝土箱梁,材料为C55混凝土,梁高按二次抛物线形变化,主塔支点处梁高9.5 m,边支点、辅助墩顶和中跨跨中梁高5.5 m。箱梁顶宽13.8 m,底宽11.3 m。箱梁中心线上设置1道中腹板,形成单箱双室截面,索梁锚固点梁部顶板处设置高1.9 m、宽0.5 m的矩形横梁,斜拉索锚固于外腹板外侧的横梁悬臂端锚固块上。主梁关键截面构造见图2、图3。全桥在支点和主跨跨中位置处设置6道横隔板,其余位置均不设置横隔板,以减轻箱梁自重。
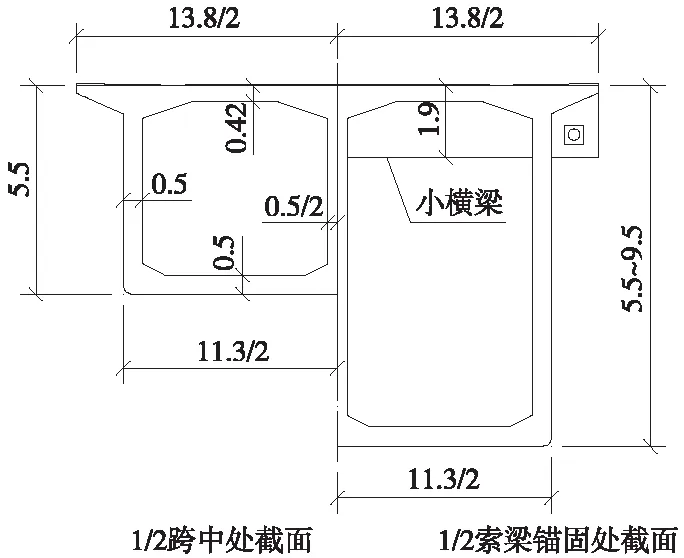
图2 主梁关键截面构造(单位:m)
主塔为双柱式混凝土桥塔,塔高28 m,主梁顶面2 m以下的塔柱采用C55混凝土,与主梁浇筑一体,其余部分塔柱采用C50混凝土,双柱间无横梁连接,见图3。塔柱采用带圆倒角的实体矩形截面,顺桥向宽3.5 m,横桥向宽2.0 m。主塔下桥墩为圆端形实心桥墩,采用C45混凝土,141号墩高18.5 m,142号墩高11.5 m。基础均为钻孔灌注桩基础,主墩基础桩径为2 m,边墩和辅助墩基础桩径为1.5 m。
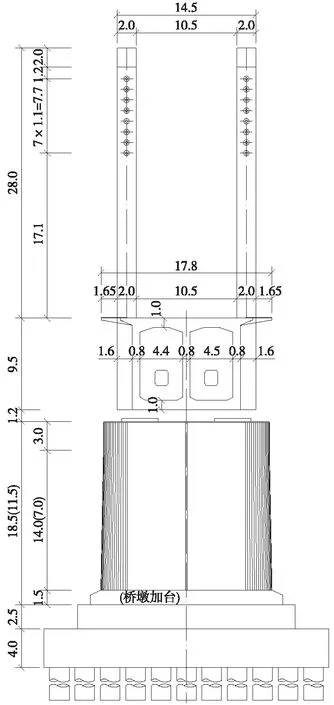
图3 主塔墩构造(单位:m)
斜拉索横向布置为双索面形式,立面布置为扇形形式,斜拉索锚固于塔柱上段1/3高度范围内,塔上索距为1.1 m,梁上索距为8 m。斜拉索通过索鞍构造在桥塔上连续通过,两侧对称锚固于梁体,索体采用环氧树脂钢绞线,规格为55-7φ5 mm和61-7φ5 mm两种。每个主塔设置8对斜拉索,全桥共16对斜拉索。
2 计算模型
采用Midas Civil 建立全桥有限元模型,主梁、桥墩和桥塔等构件采用梁单元模拟,斜拉索采用索单元模拟,桩基础刚度采用刚度矩阵模拟,共计245个梁单元、64个索单元,见图4。收缩徐变理论计算模型依据TB10092—2017《铁路桥涵混凝土结构设计规范》中相关条文执行,环境湿度取55%,加载龄期按3 d考虑。
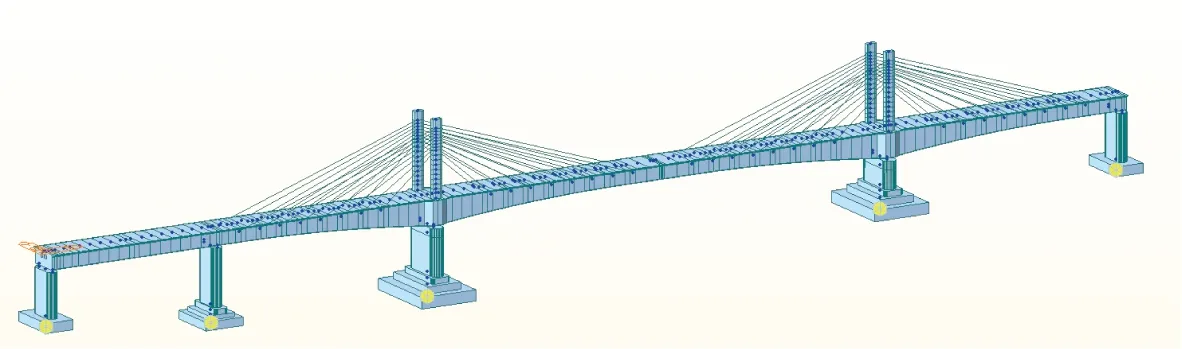
图4 全桥有限元模型
施工阶段按有索跨分节段悬臂现浇施工、无索边跨满堂支架现浇施工的设计步骤模拟,其中,终张拉斜拉索60d后铺设无砟轨道,取运营3个月、6个月、1年、3年、5年、10年、20年和30年等8个阶段,并分析收缩徐变对这8个阶段结构变形和内力的影响。
3 运营阶段收缩徐变效应分析
3.1 收缩徐变对结构变形的影响
收缩徐变对矮塔斜拉桥结构变形的影响主要体现在主梁、桥塔和斜拉索等三大主要构件的变形上。因斜拉索两端分别锚固在主梁和桥塔上,这里主要分析收缩徐变对主梁和桥塔变形的影响。
(1)收缩徐变对主梁变形的影响
以成桥时主梁线形为基准,在混凝土的收缩徐变作用下,主梁不同运营阶段的竖向挠度见图5(主梁挠度向下为负,反之为正),收缩徐变引起的第一至四跨跨中竖向挠度随时间的变化规律见图6。

图5 收缩徐变引起的主梁竖向挠度
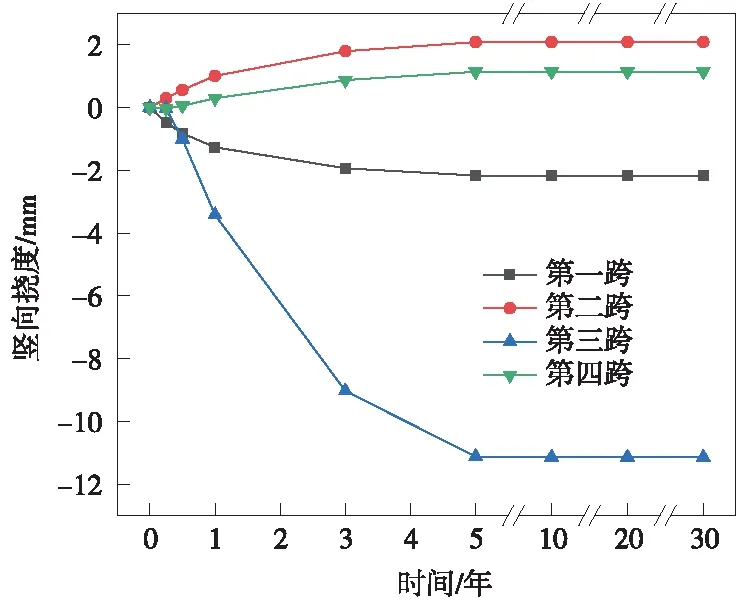
图6 收缩徐变引起的主梁各跨跨中竖向挠度
由图5、图6可知,运营期间,收缩徐变引起第一跨和第三跨下挠,最大竖向挠度分别为-2.17 mm和-11.14 mm;第二跨和第四跨上拱,最大竖向挠度分别为2.09 mm和1.14 mm。收缩徐变引起的主梁竖向挠度沿跨度方向总体呈光滑曲线分布,不存在变形突变点,距离支撑点越远的主梁截面挠度越大;随着时间的增加,收缩徐变引起主梁竖向挠度变化的速率越来越慢,收缩徐变效应逐渐减弱,运营3年后,约80%的主梁竖向挠度已经发生,运营5年后,主梁的竖向挠度趋于不变。
(2)收缩徐变对桥塔变形的影响
以成桥时主塔线形为基准,在混凝土的收缩徐变作用下,主塔塔柱不同运营阶段的纵桥向位移见图7(a)(主塔向大里程侧位移为正,反之为负)。考虑到本桥结构体系为塔梁固结、梁墩分离的连续梁体系,大里程侧桥塔处主梁设置活动支座,收缩徐变引起主梁纵桥向压缩位移,带动塔柱纵桥向位移。若剔除该效应,主塔柱的纵桥向位移见图7(b),收缩徐变引起的塔顶纵桥向位移随时间的变化规律见图8。由图8可知,运营期间,收缩徐变引起塔顶向主跨跨中位移,小里程侧塔顶最大纵向位移为2.33 mm,大里程侧塔顶最大纵向位移为-2.08 mm,且塔柱由低到高位移逐渐增大;随着时间的增加,收缩徐变引起塔顶位移的变化速率越来越慢,收缩徐变效应逐步减弱;运营3年后,约80%的塔柱的纵桥向位移已经发生;运营5年后,塔柱的纵桥向位移趋于不变,收缩徐变几乎停止。
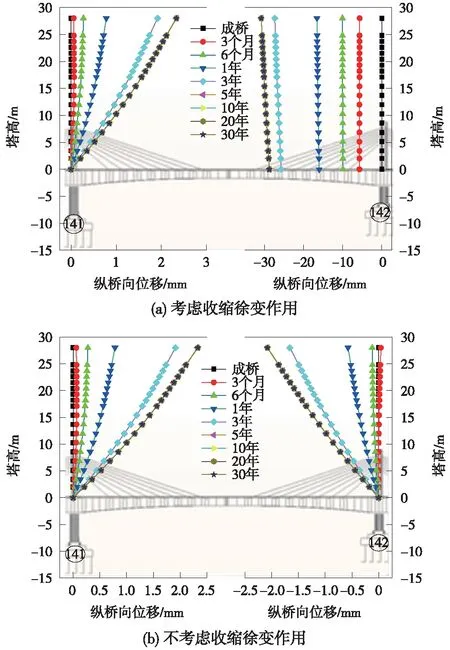
图7 收缩徐变引起的主塔柱纵桥向位移
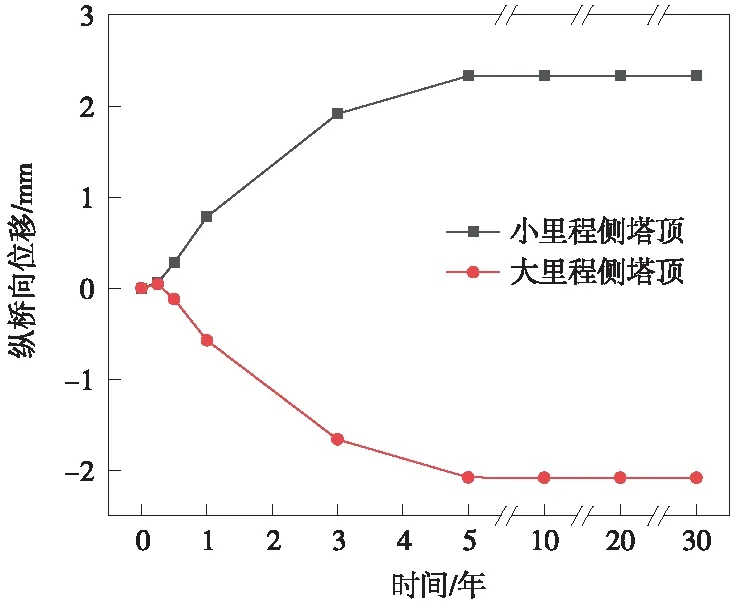
图8 收缩徐变引起的塔顶纵桥向位移
3.2 收缩徐变对结构内力的影响
(1)收缩徐变对主梁截面应力的影响
以成桥时主梁截面应力为基准,在混凝土收缩徐变作用下,不同运营阶段,主梁截面的上缘应力变化见图9(a),主梁截面的下缘应力变化量见图9(b)(截面应力受拉为正,受压为负,应力变化量为末值减初值)。铁路预应力混凝土矮塔斜拉桥常规设计时,主梁一般按照全预应力构件设计,即运营期间主梁各截面全截面受压。由图9可知,运营期间,收缩徐变引起第一跨主梁跨中附近截面上缘应力变化很小,截面下缘压应力减小;140号墩墩顶附近主梁截面上缘压应力减小,截面下缘压应力几乎不变;141和142号墩墩顶主梁截面上缘压应力减小,截面下缘压应力增大;主跨跨中附近主梁截面上缘压应力增大,截面下缘压应力减小;随着时间的增加,收缩徐变引起主梁截面上、下缘应力的变化速率越来越慢,收缩徐变效应渐渐减弱;运营3年后,约80%的主梁截面应力变化已经发生;运营5年后,主梁截面上、下缘的压应力趋于不变。
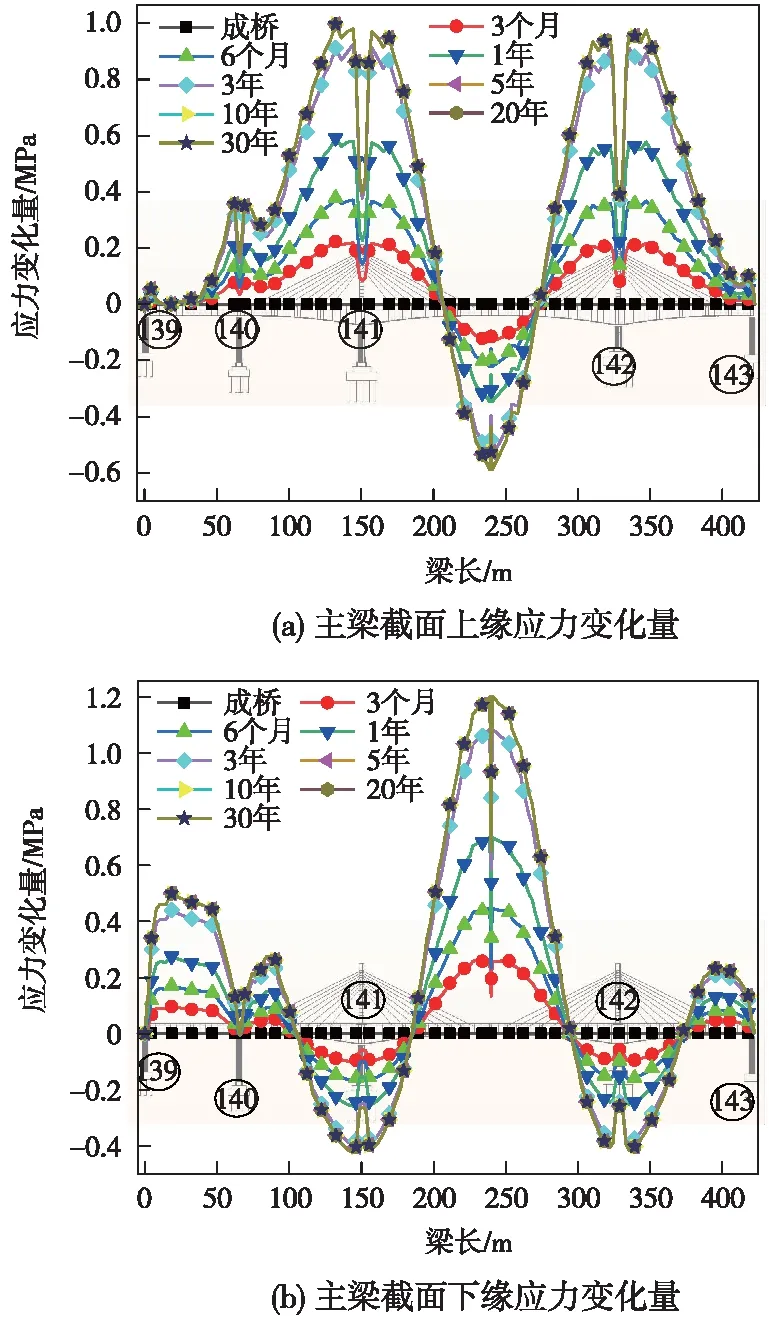
图9 收缩徐变引起的主梁截面上下缘应力变化量
(2)收缩徐变对塔柱截面应力的影响
以成桥时主塔塔柱截面应力为基准,不同运营阶段,在混凝土的收缩徐变作用下,主塔柱截面应力变化见图10。由图10可知,运营期间,收缩徐变引起塔柱截面压应力逐渐减小;随着时间的增加,收缩徐变引起塔柱截面压应力减小的速率越来越慢,收缩徐变效应减弱;运营3年后,约80%的塔柱截面应力变化已经发生;运营5年后,塔柱压应力趋于不变,收缩徐变几乎停止。混凝土结构压应力越大,徐变效应越大[20],一般情况下,收缩徐变引起塔柱截面应力变化量从上到下逐渐增大;混凝土强度等级越高,相同压应力水平下徐变越小,塔柱最下端的2 m段为C55混凝土,其余部分塔柱为C50混凝土。因此,该处收缩徐变引起的应力变化量相对较小。
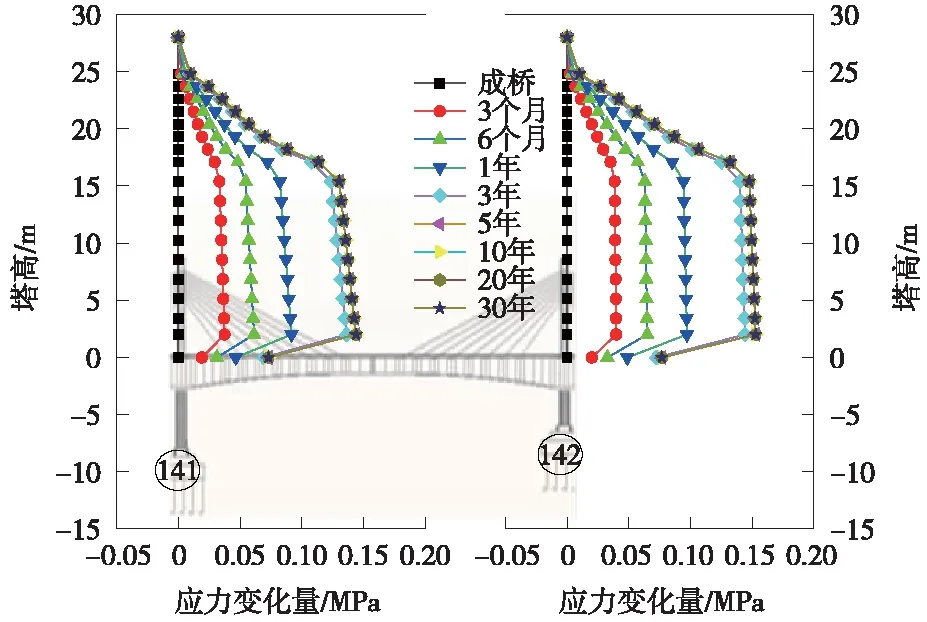
图10 收缩徐变引起的主塔塔柱截面应力变化量
(3)收缩徐变对斜拉索索力的影响
以成桥时斜拉索索力为基准,在混凝土收缩徐变作用下,不同运营阶段斜拉索索力变化量见图11(斜拉索索力受拉为正,反之为负,索力变化量为末值减初值)。由图11可知,运营期间,收缩徐变引起斜拉索索力逐渐减小;随着时间的增加,收缩徐变引起斜拉索索力减小的速率越来越慢,收缩徐变效应减弱;运营3年后,约80%的斜拉索索力变化已经发生;运营5年后,斜拉索索力趋于不变。
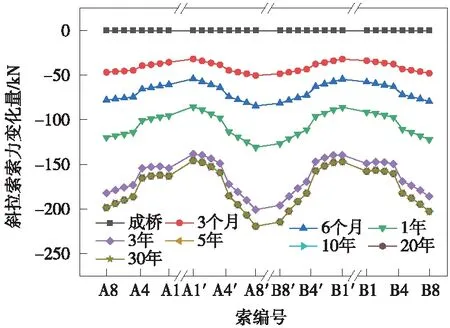
图11 收缩徐变引起的斜拉索索力变化量
4 非对称施工对结构收缩徐变的影响
受施工现场大里程侧高压输电塔拆迁等因素影响,潮白河特大桥主桥实际施工时,142号墩侧的主梁悬臂施工进度141号墩侧的主梁悬臂施工进度滞后约半年,存在非对称施工问题。可利用计算软件中的荷载功能模拟这种非对称施工过程,并分析其对运营阶段结构收缩徐变变形的影响。
4.1 对主梁收缩徐变的影响
以成桥时主梁线形为基准,在混凝土的收缩徐变作用下,不同运营阶段的主梁竖向挠度见图12。
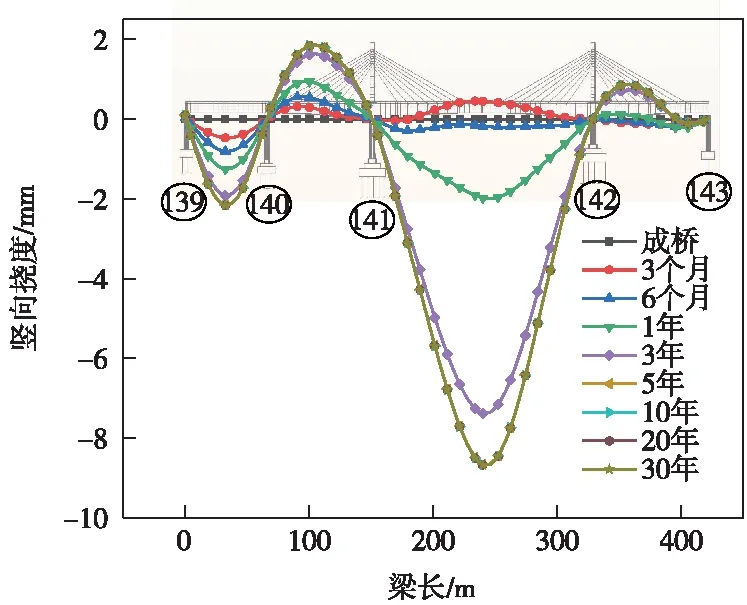
图12 收缩徐变引起的主梁竖向挠度
由图12可知,运营期间,收缩徐变作用下,早期第三跨主梁有上拱的趋势,第四跨主梁有下挠,后期第一跨和第三跨主梁下挠,最大竖向挠度分别为2.16 mm和8.68 mm;第二跨和第四跨主梁上拱,最大竖向挠度分别为1.84 mm和0.61 mm。相较于原设计,收缩徐变引起的运营阶段主梁竖向挠度有所减小,其中主跨(第三跨)主梁竖向挠度减小22.1%,对后期运营无不利影响。
4.2 对桥塔收缩徐变的影响
以成桥时主塔线形为基准,并剔除结构支承体系带来的大里程侧桥塔塔柱纵桥向位移,在混凝土的收缩徐变作用下,不同运营阶段的主塔塔柱纵桥向位移见图13。由图13可知,运营期间,收缩徐变引起塔顶向主跨跨中位移,小里程侧塔顶最大纵向位移1.79 mm,大里程侧塔顶最大纵向位移1.61 mm,且塔柱由低到高位移逐渐增大;相较于原设计,收缩徐变引起的运营阶段塔柱纵桥向位移有所减小,其中小里程和大里程桥塔塔顶纵桥向位移分别减小23.2%和22.6%,对后期运营无不利影响。

图13 收缩徐变引起的主塔柱纵桥向位移
5 结论
针对京沈高铁潮白河特大桥主桥,运用有限元方法分析了运营阶段高速铁路预应力混凝土矮塔斜拉桥的收缩徐变效应,得到以下结论。
(1)收缩徐变作用下,主跨主梁下挠,有斜拉索锚固的边跨主梁上拱,无斜拉索锚固的边跨主梁下挠,桥塔向主跨跨中变形的趋势,运营3年后,约80%的结构变形已经发生,5年后趋于不变。
(2)收缩徐变作用下,主塔处主梁上缘压应力减小,下缘压应力增大,主跨跨中处主梁上缘压应力增大,下缘压应力减小,运营3年后,约80%的主梁截面应力变化已经发生,5年后趋于不变。
(3)收缩徐变作用下,主塔塔柱和斜拉索的内力均减小,运营3年后,约80%的主塔塔柱和斜拉索内力变化已经发生,运营5年后,主塔塔柱和斜拉索内力趋于不变。
(4)收缩徐变对预应力混凝土矮塔斜拉桥结构的变形和受力影响呈现出早期大、后期小和早期变化快、后期变化慢的规律。运营3年后,约80%的结构变形和受力变化已经发生,运营5年后,收缩徐变对结构变形和受力的影响已很小,故常规设计中,计算成桥后5年的收缩徐变效应即可。
(5)相较于原设计,非对称施工时,运营阶段结构收缩徐变变形有所减小,主跨主梁跨中竖向挠度减小22.1%,小里程和大里程桥塔塔顶纵桥向位移分别减小23.2%和22.6%,对后期运营无不利影响。
