一种基于LMD-PSO-SVR的涉铁变形监测信号粗差探测与修复方法

陈旭升

(中国铁路设计集团有限公司，天津 300251)

涉铁变形监测主要有实时自动化监测方法和人工周期监测方法。在自动化监测过程中，静力水准仪等会受到温度、大气等各种环境因素以及传感器自身的影响，且自动化变形监测信号通常具有非线性、非平稳的多尺度特性[1]，易造成粗差，粗差会影响信号处理的正确性和信号分析的精确性。因此，针对自动化变形监测信号进行粗差探测与修复是信号预处理阶段中一项重要的任务[2]。

常用的粗差探测方法有狄克松判别法和t检验法等，但是针对非线性、非平稳的自动化变形监测信号，这些方法均有一定的局限性[3-4]。针对该类粗差探测与修复问题，已有许多学者开展相关研究，张金华等通过小波变换系数的模量极大值检测出周跳，然后通过小波变换重构GPS信号实现信号的修复处理[5]；王奉伟等通过LMD分解大坎原始监测数据的PF分量定位粗差位置并剔除，然后利用三次样条插值修复处理[6]。此外，还有学者提出组合预测方法，孔庆燕等利用粒子群算法(Particle Swarm Optimization，PSO)结合支持向量回归机(Support Vactor Regerssion，SVR)，建立了PSO-SVR的预报模型对低温雨雪冰冻过程的冷湿指数进行业务预报试验[7]；王仁超等采用布谷鸟搜索算法(Cuckoo Search，CS)结合核极限学习机(Extreme Learning Machine，ELM)，建立了CS-KELM预测模型并对某水坝坝体的变形位移进行预测[8]。

局部均值分解(Local Mean Decomposition，LMD)作为一种新的时频分析手段[9]，相较于传统的小波分析方法和经验模态分解方法有其自身的优势，使得LMD在非线性、非平稳的变形监测数据处理及分析中得到了广泛应用[10]。为了对铁路桥墩自动化变形监测信号进行粗差探测与修复，构造了基于LMD-PSO-SVR的粗差探测与修复方法：首先利用LMD对原始自动化变形监测信号进行分解处理，然后利用支持向量回归机对分解的各PF分量进行预测，利用粒子群算法对SVR的核心参数进行优化，以此完成自动化变形监测信号的粗差探测与修复工作。

1 粗差探测与修复方法

1.1 局部均值分解

对于给定的变形监测信号x(t)，其局部均值分解过程如下[9]。

(1)确定原始信号x(t)的所有局部极值点ni及其极值x(ni)，计算两个相邻极值点ni和ni+1的局部均值mi和局部幅值ai；采用滑动平均法处理局部均值和局部幅值，计算出局部均值函数m11(t)和包络估计函数a11(t)。

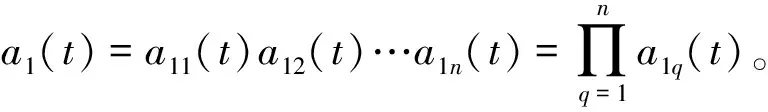
(3)将包络信号a1(t)与纯调频信号s1n(t)相乘，得到第一个乘积函数：PF1(t)=a1(t)s1n(t)。

(4)将PF1(t)从原始信号x(t)中剔除，得到新的信号u1(t)，整个过程需要重复k次，直至uk(t)单调。

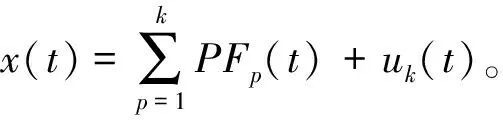
由基本原理可知，LMD算法包含有内外两层迭代循环的过程，其中内层循环的目的是得到纯调频信号，外层循环的目的是得到每一个乘积函数。

1.2 支持向量回归机

SVM在求解二分类问题中的目的是使到划分超平面最近样本点的“距离”最大，而SVR是使到最优分类面最远样本点的“距离”最小。用于解决回归问题的ε-SVR的基本型为[11-12]

(1)

(2)

式中，C为惩罚因子；ε为不敏感损失函数参数；ξ、ξ*为松弛变量。该基本型是一个凸二次规划问题，其对偶问题为

(3)

(4)

(5)

SVR的核心参数为惩罚因子C、核函数参数σ及不敏感损失函数参数ε，核心参数的选取是否合理，将会直接影响所建立的回归模型的泛化能力和精度。因此，选用PSO算法对SVR的核心参数进行优化，以达到最优回归结果。

1.3 粒子群算法

PSO算法是模拟鸟群觅食过程而提出的一种通过迭代循环求解最优参数解的算法，PSO算法原理如下[13-14]。

假设在D维空间中有m个粒子构成一个种群，则在时刻t粒子i的位置和速度分别为

(6)

(7)

在时刻t，粒子i及种群的历史最优位置分别为

(8)

(9)

在时刻t+1，粒子i的速度和位置分别为

(10)

(11)

式中，w为惯性权重因子；c1和c2为学习因子；r1和r2为属于[0，1]的随机数。

PSO算法优化SVR核心参数的步骤如下所述。

(1)初始化粒子群，设置PSO的基本参数，将初始种群中的每个粒子解码为SVR模型的C、σ及ε参数值。

(3)重复进行步骤(2)，直至迭代次数或全局最优解的适应度达到预设值，则获取最优Cbest、σbest及εbest，以此优化SVR回归模型。

1.4 LMD-PSO-SVR粗差探测与修复方法

为了探测变形监测信号中的粗差，构造基于LMD-PSO-SVR的变形监测信号粗差探测与修复方法：利用LMD对变形监测信号进行多尺度分解，粗差信息表现为监测信号中的奇异成分，且属于信号中的第一类间断点[15]，根据信号的奇异性检测原理，当出现粗差时，反映为PF分量瞬时幅值函数(即上文所述包络信号)极大值的位置[16]，便可以定位粗差，并且剔除粗差，然后利用PSO优化的SVR对剔除粗差后的监测信号进行修复处理。基于LMD-PSO-SVR的变形监测信号粗差探测与修复方法的基本步骤如下。

(1)对包含粗差的原始自动化变形监测信号执行LMD分解，得到k个PF分量和一个残余分量uk(t)。

(2)求取PF分量瞬时幅值函数的标准差σ，若瞬时幅值函数的模极大值大于3σ，表示该值为异常值[17]，实施粗差的探测过程，进而剔除粗差。

基于LMD-PSO-SVR的粗差探测与修复流程见图1。

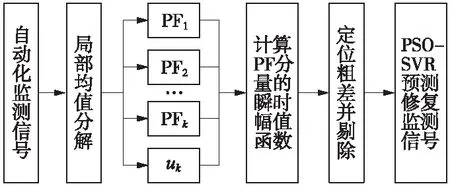
图1 基于LMD-PSO-SVR的粗差探测与修复流程

2 实例分析

2.1 粗差探测

涉铁监测项目中，要求采用自动化设备监测铁路建(构)筑物的变形情况，以此分析施工对铁路建(构)筑物带来的影响。液体静力水准仪采集的桥墩沉降信号通常具有非线性、非平稳及数据量大等特点，信号主要包含3个方面的内容：(1)基坑开挖、区域降水及桥墩自身荷载而产生的真实沉降，该分量通常表现为低频变化；(2)风力、温度变化等环境因素影响而产生的测量噪声，该分量通常表现为高频变化；(3)现场施工振动监测设备等影响而产生的测量粗差，该分量通常变形为突变异常变化。

依据《高速铁路工程测量规范》，铁路桥墩尤其是高铁桥墩属于变形比较敏感的重要工程设施，若自动化变形监测信号中包含粗差，则必然会影响信号处理和信号分析的准确性及真实性，甚至有可能会造成变形误报警等严重后果。因此，需要在监测信号预处理阶段对粗差进行处理。由上文分析可知，这种包含粗差的非线性、非平稳类型的自动化变形监测信号适合采用所提出的方法进行分析处理。

使用液体静力水准仪对下穿铁路某桥墩进行监测，获取共计1 024期的沉降监测信号，见图2。所采用的液体静力水准仪的标准量程为100 mm，数据采样间隔为1 h/期。图2中，纵轴表示桥墩累积沉降量，横轴表示监测期数。原始监测信号中不包含粗差，为说明提出的LMD-PSO-SVR粗差探测与修复方法的实用性，在原始监测信号第200期和第815期中分别加入已知粗差。加入粗差后的沉降监测信号见图3。

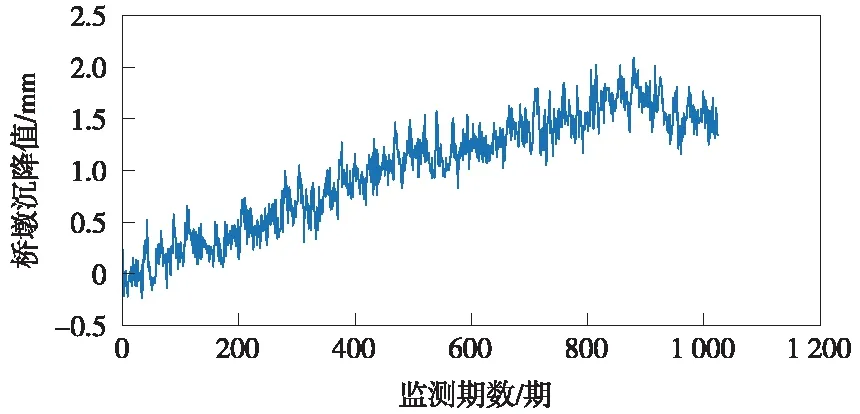
图2 桥墩沉降原始监测信号

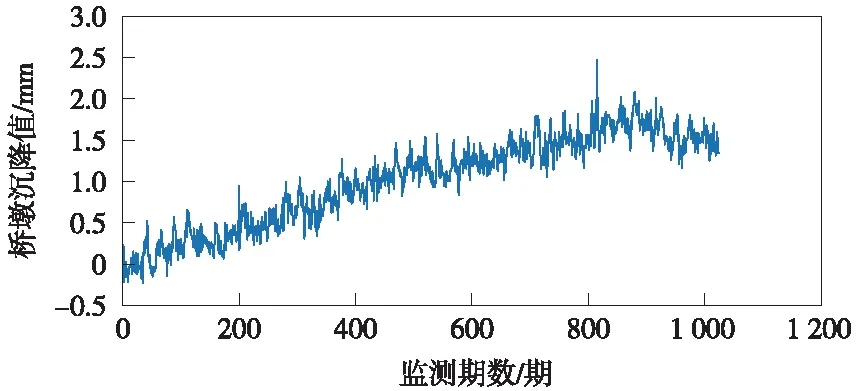
图3 桥墩沉降监测信号(包含粗差)

为了探测粗差，将非线性、非平稳的监测信号按照频率尺度特性分解得到较为平稳的PF分量，同时结合SVR较好的学习能力和泛化能力，构建基于LMD-PSO-SVR的粗差探测与修复方法对监测信号进行处理。此外，由于粗差表现为监测信号中的奇异成分，包含有粗差的监测信号经LMD分解后，粗差会被分解到高频PF分量中，故一般可以通过第一个或前几个高频PF分量反映[18]。桥墩沉降监测信号经LMD分解的结果见图4，求取各PF分量的瞬时幅值谱见图5。由图5可知，在第200期及第815期处的瞬时幅值函数出现极大值点且其值均大于3σ，其余历元处的瞬时幅值函数值未均大于3σ。因此，可以判断原始监测信号在这两个历元包含粗差，至此实现了粗差的探测过程。

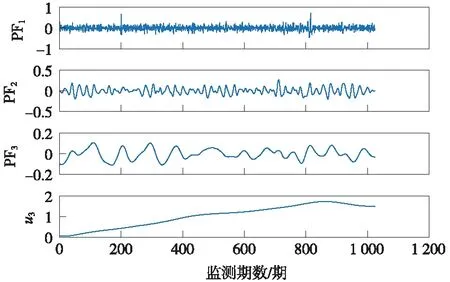
图4 桥墩沉降监测信号的LMD分解结果(单位：mm)

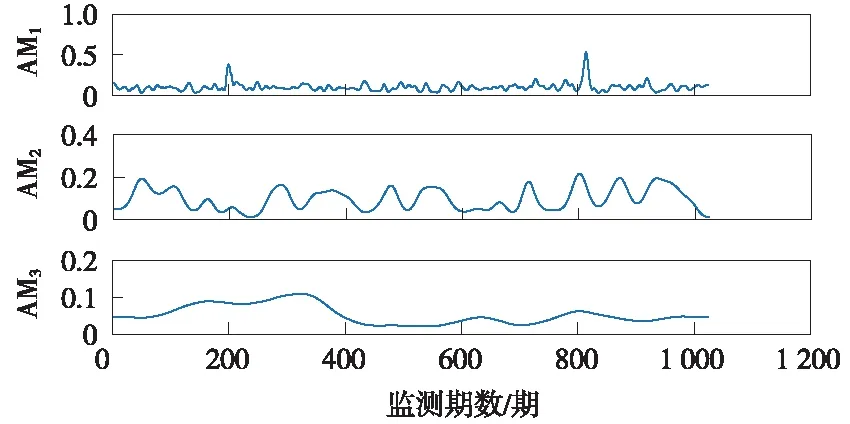
图5 PF分量的瞬时幅值谱(单位：mm)

同时作为对比，采用EMD法对桥墩沉降监测信号进行分解处理，EMD分解的结果见图6，求取各IMF分量的Hilbert谱见图7。由图6可知，相较于LMD的分解结果，EMD分解得到了更多数量的IMF分量，由于较多的IMF分量中可能包含伪分量，针对IMF伪分量的预测结果也无意义。由图7可知，EMD分解IMF分量的Hilbert谱在第326期、557期、735期及913期的模极大值点数值均大于3σ，即由EMD的分解结果出现多处误判的情况。EMD分解结果中，这两种现象对于变形监测信号粗差的探测与修复不利。从这个角度分析，提出的基于LMD的粗差探测方法优于基于EMD的粗差探测方法。

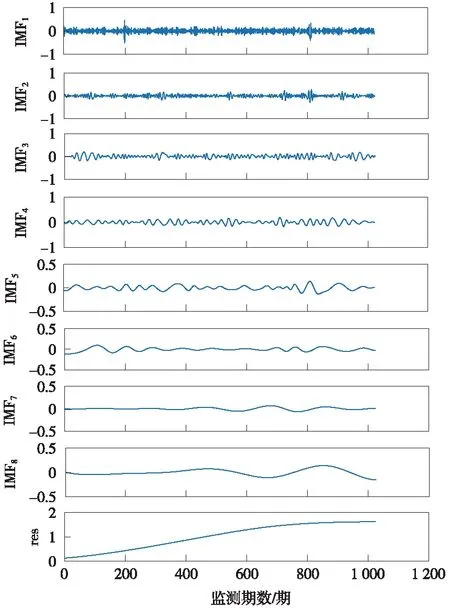
图6 桥墩沉降监测信号的EMD分解结果(单位：mm)

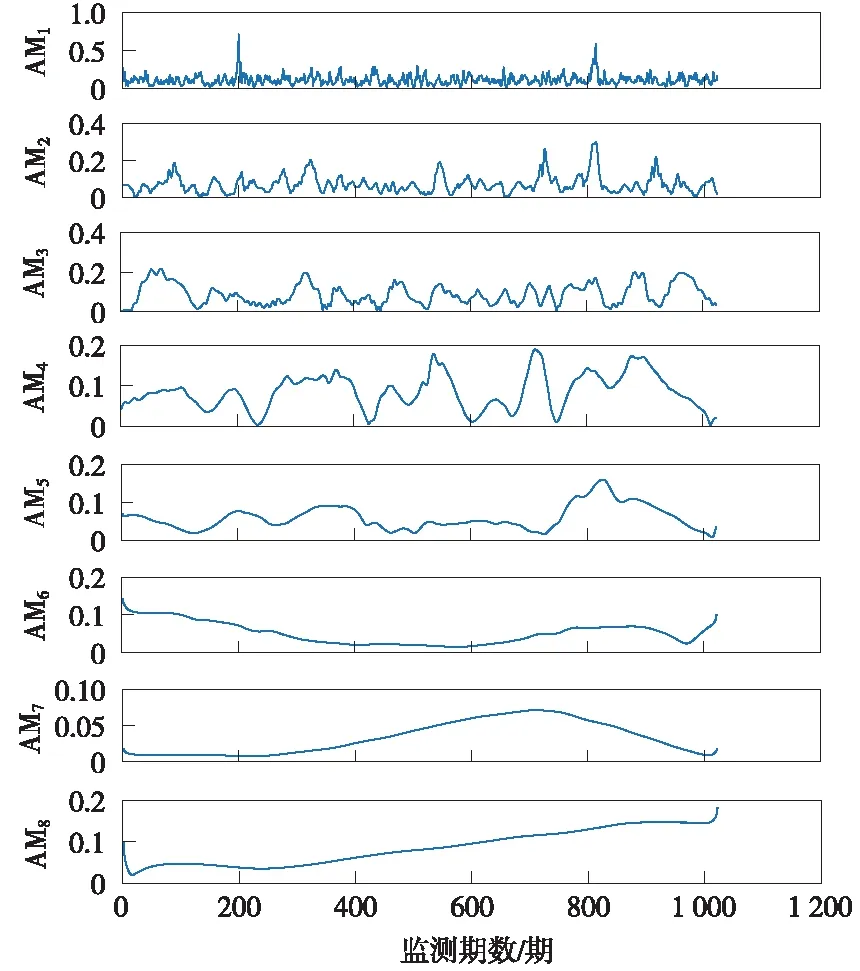
图7 IMF分量的Hilbert谱曲线(单位：mm)

2.2 粗差修复

定位粗差发生历元后便可剔除粗差，然后进行监测信号修复工作。分别利用LMD-SVR及LMD-PSO-SVR对监测信号的PF1分量进行预测修复实验，且取193-200期这8期的数据作为测试数据集用以评定两种方法的预测修复精度，两种方法的精度评价指标见表1。

表1 2种方法精度评价指标 mm

由表1可知，由于LMD-SVR未使用PSO优化选取SVR的核心参数C、σ及ε，虽然LMD-SVR的平均绝对误差和均方根误差较小，但其预测能力还有待进一步提高。而采用PSO优化选取SVR的核心参数后，使得LMD-PSO-SVR的预测精度更高，从而证明了该方法在信号预测修复方面的有效性和可靠性。

采用第2节所述的预测模型，利用粗差发生历元前的PF分量PF1～PF3及残余分量分别建立SVR的训练模型，同时对于SVR的3个核心参数采用PSO算法进行优化选取，以此得到粗差发生历元处的预测值u1～u4。其中，利用PSO优化的SVR对PF1分量预测时，设定种群个数为20，终止代数为100，最小权重因子为0.4，最大权重因子为0.9，学习因子为1.5，嵌入维数为10。对PF2、PF3及残余分量预测时的参数设置基本类似，这里不再赘述。各PF分量及残余分量的预测值，以及最终的修复值、实测值和残差绝对值见表2。采用不经过PSO优化参数的LMD-SVR预测模型的计算结果见表3。

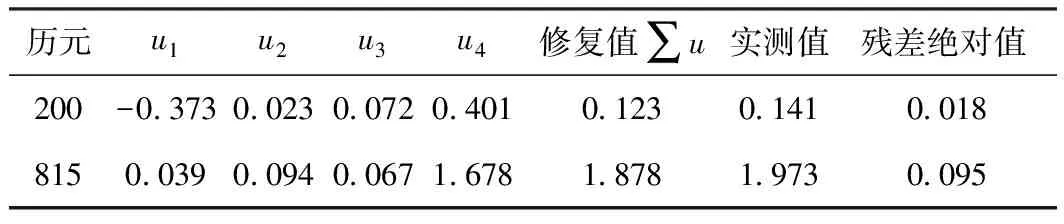
表2 LMD-PSO-SVR修复值与实测值对比 mm

表3 LMD-SVR修复值与实测值对比 mm

由表2、表3可知，在第200期和第815期处，采用LMD-PSO-SVR法对单个PF分量分别建立预测模型，然后叠加各个分量的预测值，各历元处的修复值与实测值的残差绝对值均小于0.1 mm，对监测信号的修复值与实测值基本一致，具有较高的预测精度；而采用LMD-SVR法对单个PF分量分别建立预测模型，然后叠加各个分量的预测值，在第815期处的修复值与实测值的残差绝对值大于0.4 mm，严重影响粗差的修复精度，LMD-SVR法对于粗差的修复精度远低于LMD-PSO-SVR法的精度。综上，提出的基于LMD-PSO-SVR的自动化变形监测信号粗差探测与修复方法具有一定的可行性，粗差探测效果良好，SVR修复值的可信度也较高。

3 结论

涉铁工程自动化变形监测采集设备受环境等多种因素的影响，使得测量信号中存在粗差，在变形分析及变形预报前需对其进行预处理，否则会影响信号处理的正确性和信号分析的精确性。提出一种基于LMD-PSO-SVR的自动化变形监测信号粗差探测与修复方法，将LMD、PSO及SVR相结合，原始自动化监测信号首先经LMD分解，利用PF分量瞬时幅值函数模极大值位置定位粗差发生的历元，然后利用PSO优化的SVR对信号进行预测修复处理，对液体静力水准仪采集的某铁路桥墩监测信号进行粗差探测处理，结果表明，该方法不仅可准确定位粗差位置，还可对剔除粗差后的信号进行较为精确的修复，各历元处的修复值与实测值的残差绝对值均小于0.1 mm。