半球形金属橡胶构件变刚度特性研究及建模

王玮，吴乙万，蒋奉，白鸿柏，路纯红

(1.福州大学机械工程及自动化学院,金属橡胶工程研究中心,福建 福州 350108；2.河北工业职业技术大学汽车工程系,河北 石家庄 050091)

0 引言

金属橡胶是由细金属丝按特殊工艺制成的具有橡胶特性的弹性多孔金属材料.在承受交变载荷时，金属橡胶内部金属丝之间将发生相互摩擦、滑移、挤压、变形，从而耗散振动能量，起到减振、缓冲的作用[1].因金属橡胶具有耐辐照、耐高低温、耐疲劳老化等高分子橡胶材料所不具备的特点，使其成为一种可被广泛运用于航空航天、尖端军事领域的新型高弹性、大阻尼材料.航空航天领域中众多精密仪器的特殊应用需求，对隔振器提出了更宽的隔振频带要求，这对金属橡胶的刚度特性提出了更苛刻的要求(更低的刚度乃至负刚度).

近年来,诸多学者对金属橡胶的力学性能及力学模型进行了研究[2-4].在力学性能研究方面，杨佩等[5]分析不同激振量级对金属橡胶-弹簧组合减振器振动特性的影响.邹广平等[6]对金属橡胶制品的压缩和剪切性能进行系统研究，得到相对密度与变形幅值是影响金属橡胶减振器隔振性能的两个重要参数.李拓等[7]制备不同密度和厚度的编织-嵌槽型金属橡胶并对其进行相关力学试验，结果表明密度和厚度的增加会增大金属橡胶的静态刚度.李静媛等[8]基于金属橡胶内部微元螺旋卷结构，分析在螺旋卷之间不同接触形式下的刚度公式并解释了载荷作用下刚度曲线不同阶段的特性.祝维文等[9]通过正弦激励加载试验,研究不同激振力、不同阻尼元件密度、不同预紧间距以及不同布置方式对新型减振器减振效果的影响.然而目前对具有变刚度特性的金属橡胶的研究尚少.

在力学模型方面，薛新等[10]将迟滞恢复力-位移曲线分解为非线性单值曲线和椭圆，基于阻尼等效理论，建立适用于粘弹性材料的宏观唯象力学模型.曹凤利等[11]提出基于变长度曲梁的细观结构单元以及曲梁间的接触作用模型.马艳红等[12]以圆柱螺旋弹簧理论为基础，考虑横向和纵向的微元体结构排列，建立金属橡胶迟滞力学模型.邵晓宙等[13]将金属橡胶构件的变形分为“等容部分”和 “体积部分”建立一种适用于工程计算和数值仿真的金属橡胶Mooney-Rivlin修正模型.Sherwood等[14]在研究泡沫铝材料的基础上建立包含密度、温度、应变率、形状函数项的经验力学关系Sherwood-Frost力学模型.李拓等[15]基于Sherwood-frost本构方程,并结合材料的特点对考虑温度效应的编织-嵌槽型金属橡胶本构方程的组成及各项的表达形式进行讨论及确定，最后通过仿真对本构方程进行验证.Qi等[16]针对泡沫铝内部结构的复杂性和不规则性,很难建立能够准确反映这种结构的三维模型的问题，提出球形泡沫铝三维建模的球形核分层算法，并利用该算法成功构建了具有随机孔隙的球形泡沫铝三维模型.

目前，金属橡胶材料常被制成圆柱形、方形、圆环形等常规形状，对刚度的降低空间十分有限.为使金属橡胶具备更低的刚度特性，改变金属橡胶构件的空间构型将是一个有益的探索方向.魏浩东等[17]研制一种草帽形金属橡胶隔振器，得出其平均刚度随相对密度增大而增大、随变形量的增大而递减的结论，但该结构并未出现明显的负刚度特性.

为满足某些极端工况对金属橡胶减振器的负刚度需求，克服金属橡胶低频减振极限，本研究设计并制作一种具有负刚度性能的半球形金属橡胶构件，并对其进行准静态压缩试验，对比研究不同相对密度的半球形金属橡胶构件的力学性能.另外，以Sherwood-Frost方程为基础，结合半球形金属橡胶构件的准静态压缩过程特点，建立半球形金属橡胶准静态压缩力学模型.

1 半球形金属橡胶构件的设计

为满足金属橡胶构件特殊的负刚度特性需求，突破金属橡胶减振器低频减振极限，设计一种具备负刚度效应的半球形金属橡胶构件.该构件采用特殊构型的模具分级冲压制备而成，半球形金属橡胶冲压模具及样件示意图如图1所示.

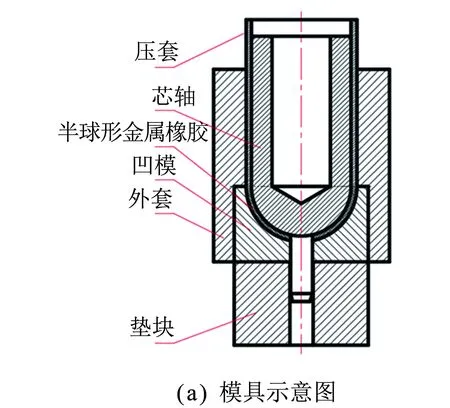
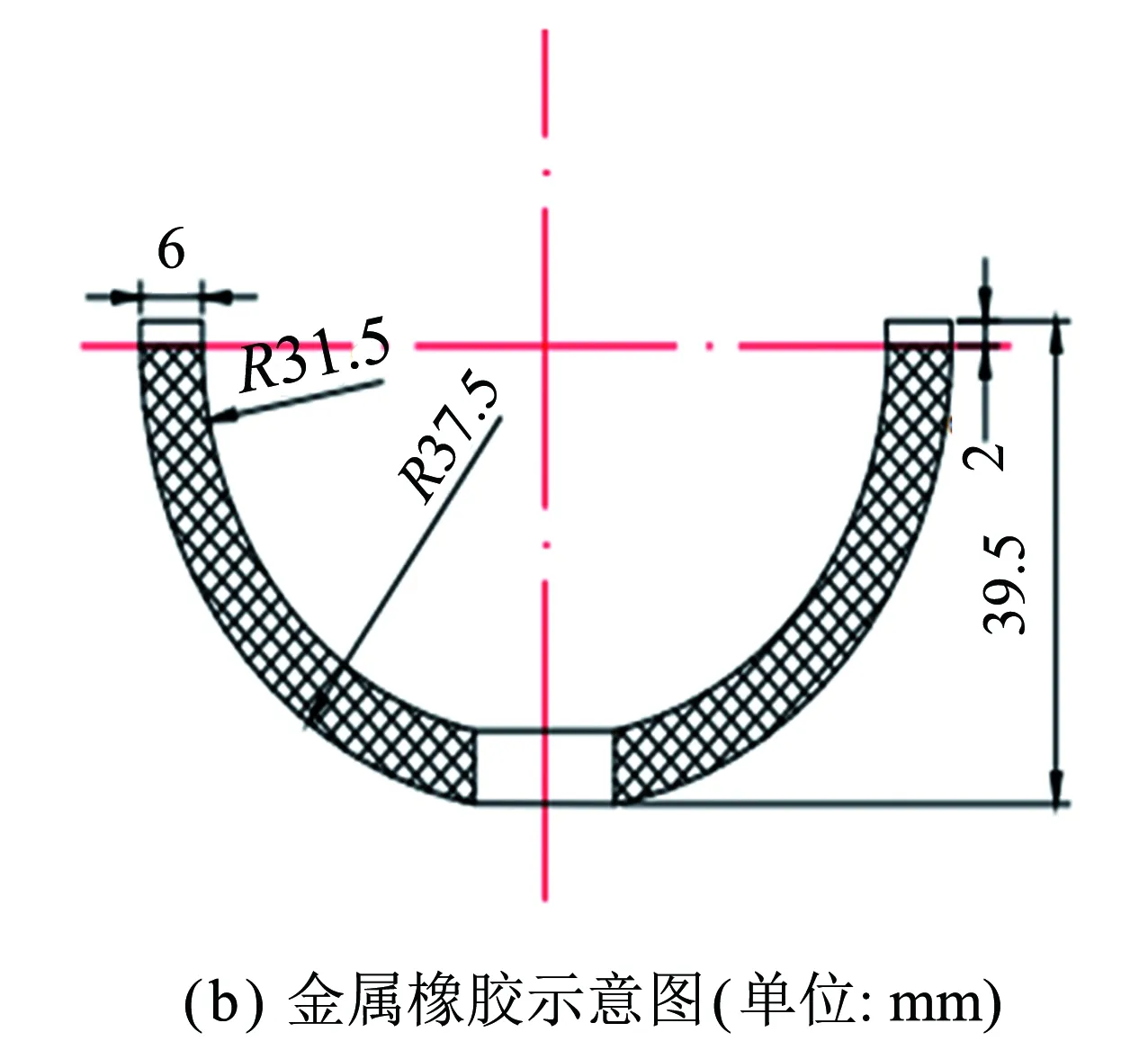
图1 成型模具及金属橡胶样件

采用丝径为0.3 mm的0Cr18Ni9Ti奥氏体不锈钢丝制作半球形金属橡胶构件.具体制作流程如下：① 将不锈钢密匝螺旋卷拉伸至螺距为3 mm的稀疏螺旋卷并均匀缠绕在芯轴上；② 将缠绕好的毛坯按图1所示方式组装好放入模具中；③ 进行分步冷压成型.为研究相对密度对试件力学性能的影响，制作3组不同相对密度试件，其相关尺寸如表1所示.

表1 半球形金属橡胶相关尺寸Tab.1 Hemispherical metal rubber related dimensions

(1)

式中：ρ为金属橡胶密度(g·mm-3);ρs为基体(304不锈钢丝)密度(g·mm-3);φ为金属橡胶材料孔隙率.

由式(1)可知，金属橡胶相对密度越小，孔隙率越大.

2 半球形金属橡胶静态压缩实验

2.1 实验设备及方法

采用济南天辰WDW-T200型电子万能试验机对半球形金属橡胶构件进行准静态加载实验.该试验机最大试验力200 kN，移动速度为0.01～500 mm·min-1，变形分辨率为0.001 mm，载荷分辨率为1 N.采用等速位移的加载方式对半球形金属橡胶构件进行加载，加载速度为1.5 mm·min-1，加载最大位移为25 mm.

2.2 表征量

图2 典型力-位移曲线Fig.2 Typical force-displacement curve

相对密度为0.29的半球形金属橡胶试件在准静态压缩条件下的典型力-位移曲线如图2所示.由图2可知，半球形金属橡胶刚度与位移量并不是单一的线性关系，而是包含了正刚度(图中‘A’)、准零刚度(图中‘B’)、负刚度(图中‘C’)等复杂非线性刚度特性.为更直观地表示这种刚度与压缩量之间的变化，用力-位移曲线中力增量ΔFm与变形增量Δxm的比值表征金属橡胶试件的刚度.当力增量与变形增量同步变化时，其刚度为正，反之为负.即当K>0时，金属橡胶表现为正刚度；当K<0时，金属橡胶表现为负刚度.其表达式为：

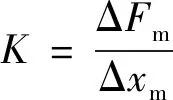
(2)

式中：Δxm为产生微位移的变形(mm)；ΔFm为产生微位移对应的力增量(N).

2.3 静态刚度特性及不同相对密度的影响

由图2可知，半球形金属橡胶的静态曲线可分为以下4个阶段.

1) 随着加载位移的增大，半球形金属橡胶恢复力逐渐增大，曲线斜率为正值，表现为正刚度特性；

2) 随着加载位移的增大，半球形金属橡胶恢复力先增大后减小，曲线斜率由正转为零再转为负值，表现出正刚度→零刚度→负刚度的特性；

3) 随着加载位移的增大，半球形金属橡胶恢复力逐渐减小，曲线斜率为负值，表现为负刚度特性；

4) 随着位移的继续增大，半球形金属橡胶恢复力先减小后增大，曲线斜率由负转为零再转为正值，表现出负刚度→零刚度→正刚度的特性.

由此可见，该半球形金属橡胶具有复杂的变刚度特性.

为研究不同相对密度对半球形金属橡胶构件静态力学性能的影响，制备了3组相对密度分别为0.26、0.29、0.32的试件.采用相同的试验方法，结果如图3所示.为便于对比分析刚度变化特性，对图3的结果进行进一步处理，获得刚度-位移曲线如图4所示.

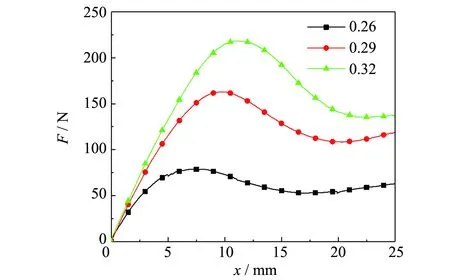
图3 不同相对密度下的力-位移曲线Fig.3 Force-displacement curves at different

图4 不同相对密度下的刚度-位移曲线Fig.4 Stiffness-displacement curves at different

由图3、4可以看出，随着相对密度的增大，刚度曲线的4个阶段均右移，这是因为随着相对密度的增大，金属橡胶内部单位体积的螺旋卷数目增加，其内部金属丝相互接触更充分，承载能力更强.另外，随着相对密度的增加，负刚度阶段形成区间逐渐增大，其负刚度峰值也显著增大，负刚度特性表现得越明显.这意味着，控制半球形金属橡胶的变形及相对密度，可获得不同的刚度特性，以满足不同的刚度需求.

采用最小二乘法对试验结果进行参数拟合，可得其刚度与位移量的函数关系：

K(0.26)=22.548-4.863x+0.224x2+0.002x3-0.000 2x4

(3)

K(0.29)=24.719+1.556x-0.974x2+0.069x3-0.001 3x4

(4)

K(0.32)=24.998+4.579x-1.256x2+0.070x3-0.001 1x4

(5)

式中：x为位移量；K为刚度.

3 半球形金属橡胶准静态力学模型的建立

图5 试件电镜图Fig.5 Electron microscopic view of specimen

金属橡胶试件微观结构的扫描电镜图如图5所示.由图中可见，金属橡胶内部各金属丝间互相交错勾连，接触状态十分复杂.在进行加载试验过程中，内部金属丝之间互相发生摩擦、挤压、滑移等运动，故对于金属橡胶材料难以像传统的高分子材料一样对其进行基于微观层面的建模.同时，本研究对象为半球形金属橡胶，其宏观空间结构的变形对半球形金属橡胶的力学性能影响较大，无法忽略空间外形对半球形金属橡胶的影响，故拟寻求一种包含形状参数项，且适用于金属橡胶试件的宏观力学模型.

20世纪90年代，Sherwood等[14]提出适用于多孔材料的较为全面的经验力学关系Sherwood-Frost模型，其一般表达形式为:

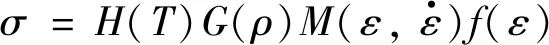
(6)

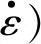
由于金属橡胶材料与泡沫铝材料都具有内部多孔的特征，其两者的弹性变形均来自于材料内部悬臂梁结构的弯曲变形，故该经验力学模型对半球形金属橡胶的力学模型的构建也同样适用.由于半球形金属橡胶的特殊空间构型，压缩应力并不是单一受压缩力的影响，由应力-应变曲线描述其准静态力学特性已不太适合，故采用力-位移曲线描述其准静态力学特性.对应地，应变率强化项转化为压缩速率项，则适用于本研究的改进Sherwood-Frost力学模型的一般表达形式为：

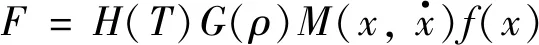
(7)

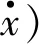
因本实验所考察的力学特性均在常温下进行测试，所选取的压缩速率较小，金属橡胶内部螺旋卷的滑移速度和内部接触点的接触状态没有明显变化，故压缩速率强化项及温度软化项可表示为：

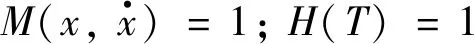
(8)

因此，常温下半球形金属橡胶准静态力学模型为：

F=G(ρ)f(x)

(9)

3.1 力学模型各参数的确定3.1.1 形状函数

金属橡胶的弹性力可由位移级数及密度项的乘积来表示，即：

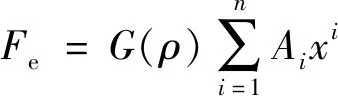
(10)

式中：Ai为多项式系数；n为多项式次数；ρ为金属橡胶的密度.

金属橡胶构件在压缩变形的过程中，其内部的金属丝之间会发生相对滑动，说明其内部还有摩擦力的存在，故金属橡胶内部所受力应包含弹性力Fe及摩擦力Ff.由文献[18]可知，金属橡胶内部摩擦力可确定为：

Ff=Feξ(1-e-λx)

(11)

式中：ξ和λ都是与内部结构接触点有关的比例系数，其与金属橡胶内部结构的接触点分布紧密相关.

因此，金属橡胶内部总的内力可表示为：

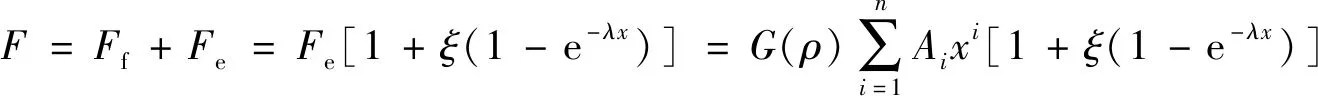
(12)

结合上式，可得形状函数的表达方式为：

(13)

3.1.2 密度项

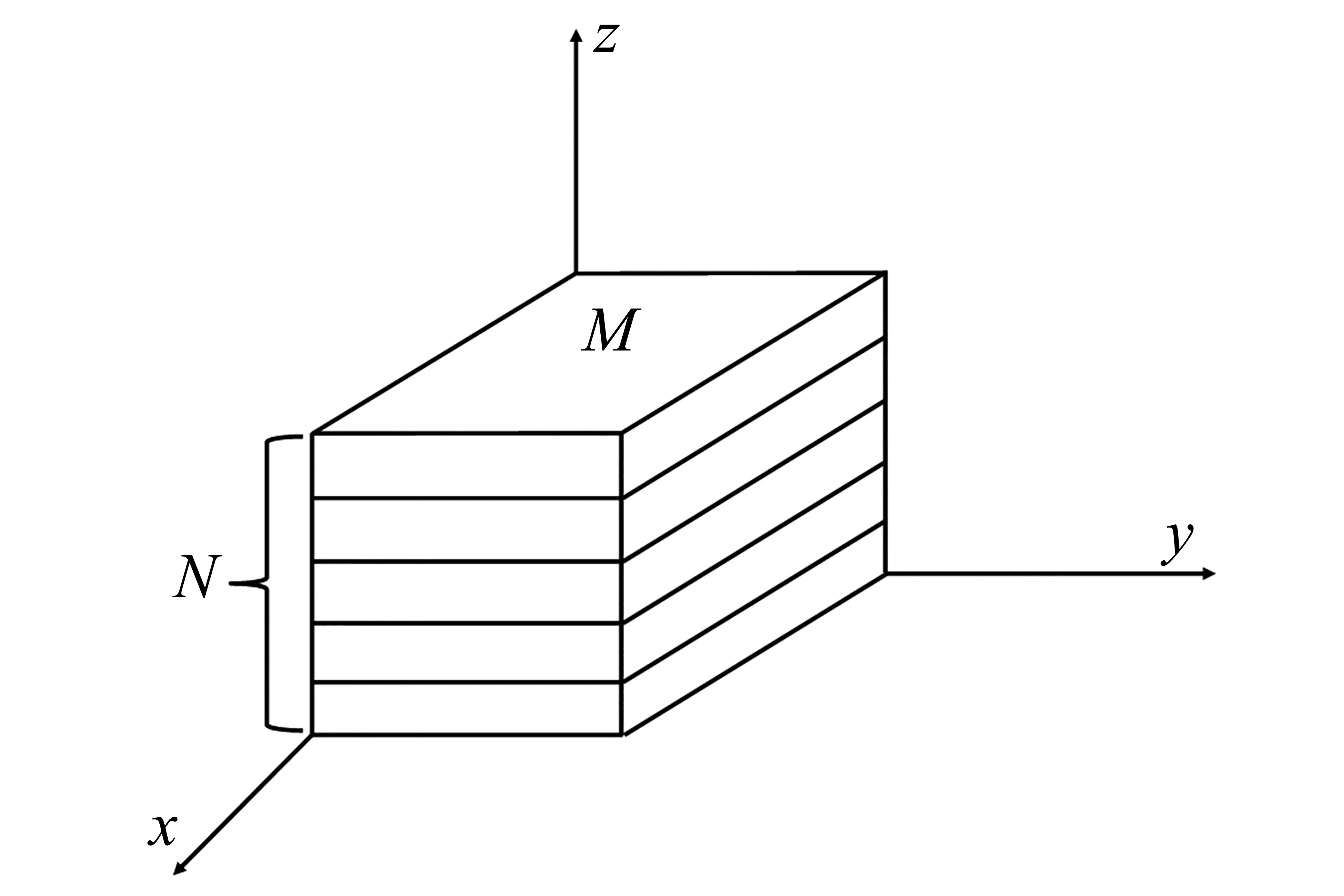
图6 串并联结构划分Fig.6 Division of series-parallel structure

建立金属橡胶细观模型时，研究人员常将金属橡胶内部简化为大量特征单元的串并联[19]，其简化结构如图6所示.

该体积单元在其成型截面上有M个结构单元，在成型界面的法向方向上有N个结构单元层，故对于一个单元体积的金属橡胶构件，可知:

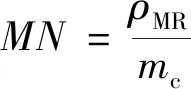
(14)

式中:mc为结构单元的质量(g).

为更好地表征密度项，做以下假设:

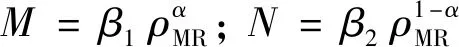
(15)

由于金属橡胶内部构造与泡沫铝材料相类似，忽略位移与密度间的耦合作用，结合以上各式，并将参考密度添加至密度项中，可知密度项的表达式为:

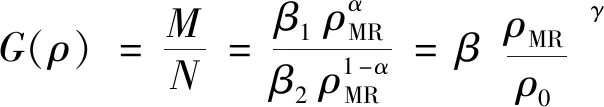
(16)

式中:β、γ均为串并联结构的比例因子，其与金属橡胶内部特征单元的排布有关.

综上分析，常温条件下半球形金属橡胶的准静态力学模型为:

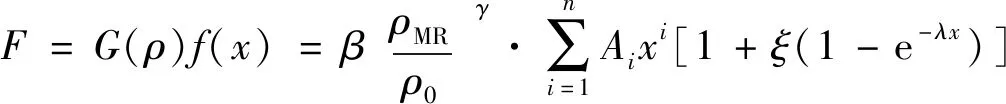
(17)

3.2 力学模型参数辨识3.2.1 形状函数的确定

设定参考相对密度，则相对密度为0.29的半球形金属橡胶在常温下的力-位移关系可表示为：

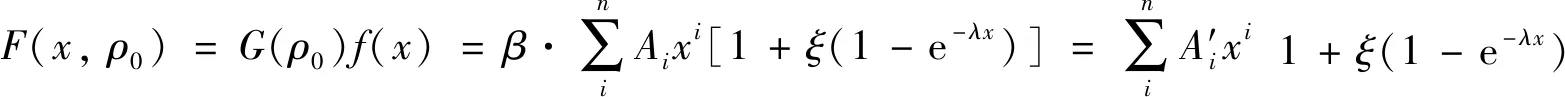
(18)

3.2.2 密度项的确定

由3.1.2可知，忽略位移与密度的耦合作用，密度项的表达式为:

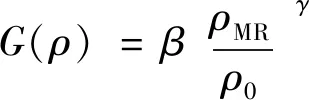
(19)

式中：β、γ均为串并联结构的比例因子；ρMR为试件相对密度；ρ0为试件参考密度.

为了得到表达式中的相关系数，取3种不同相对密度的半球形金属橡胶试件在常温下的试验数据进行最小二乘拟合，得到β=0.891 7，γ=4.099，拟合结果如图8所示.

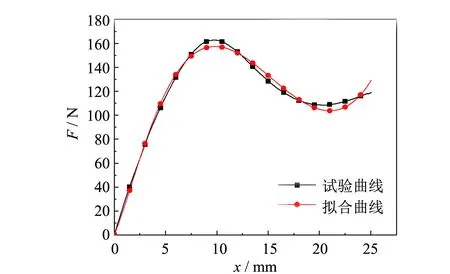
图7 形状函数拟合曲线Fig.7 Shape function fitting curve

图8 实验曲线及拟合曲线Fig.8 Experiment curves and fitting curves

为更系统地说明拟合曲线与实验曲线的贴合程度，选取位移值为5、10、15、20、25 mm的实验数据，3种试件的试验值、拟合值及误差列于表2.

表2 不同相对密度下试验值与拟合值比较Tab.2 Comparison between experiment and fitted values at different relative density

由图8及表2可知，3种不同相对密度试件的力-位移理论值与实验数据拟合较好，表明所建立静态力学模型基本能有效地预估半球形金属橡胶构件的力学性能.

4 结语

1) 设计并制备一种具有变刚度特性的半球形金属橡胶构件，研究分析相对密度对半球形金属橡胶力学性能影响，获得不同相对密度条件下的刚度-位移变化规律，可较好地预测半球形金属橡胶在不同相对密度及变形量条件下的力学变化趋势，为半球形金属橡胶在变刚度领域的应用提供借鉴.

2) 基于Sherwood-Frost力学模型，结合半球形金属橡胶构件的特点，建立由密度项及形状函数组成半球形金属橡胶准静态压缩力学模型.结合试验数据进行试验值与拟合值的对比，两类数据之间的误差大部分保持在20%以内，说明所构建的力学模型能够预测半球形金属橡胶在准静态压缩力学特性.

3) 重点考察金属橡胶相对密度对半球形金属橡胶构件力学性能特性的影响，金属丝径、制备工艺、金属橡胶几何尺寸等对其力学性能的影响仍有待进一步的研究及完善.

4) 从宏观力学建模角度出发，借鉴一般的研究思路建立适用于半球形金属橡胶的唯象力学模型，但从微观建模层面对于半球形金属橡胶力学模型的研究仍有待后续探究.