采用IEWT-SAE算法的配电变压器故障诊断方法
2022-11-25崔凤新卢思佳邱仕达
崔凤新,卢思佳,邱仕达
(1.福州大学至诚学院电气工程系,福建 福州 350002;2.福州大学电气工程与自动化学院,福建 福州 350108)
0 引言
变压器作为电力系统向用户供电的重要设备,在电能输送、分配等环节都起着要的作用,其运行状况直接影响电力系统的安全、稳定运行[1-3].变压器故障主要来自铁芯和绕组,变压器本体振动包含铁芯和绕组所在运行状态下的丰富信息[4-5].利用振动分析法对其运行状态进行辨识行之有效.文献[6]通过交叉小波变换提取变压器本体振动数据主成分,将其幅值和频率作为幅频特征量来诊断具体故障类型.文献[7]利用变分模态分解法对振动信号进行分解,对每个变分固有模态函数实施希尔伯特变换,提取时频信息作为特征量.文献[8]利用经验小波变换对变压器振动信号进行分解,并对分解后的各分量实施希尔伯特变换.为了量化特征,提取分量的多尺度熵,最后利用Fisher判别器完成故障分类.文献[9]利用无标签数据逐层训练堆栈自编码器(stacked auto-encoder,SAE),再使用有标签数据对模型进行微调,最后将提取的特征输入到随机森林中进行故障辨识.
上述处理方法在噪声干扰下分解效果不理想,主要表现为:交叉小波变换分解效果受小波基选择的影响,在提取高频分量特征时效果不好;经验小波变换需预先设置分解个数,在信号极值点的干扰下会导致频带划分不恰当.本研究使用顺序统计滤波包络法无需设置分解个数即可自适应分解信号,解决信号频带划分过密问题;使用K-L散度筛选分解后的信号,剔除信号中包含的直流分量、噪声等干扰成分;引入樽海鞘群算法(salp swarm algorithm,SSA)[10]实现SAE关键参数的自适应寻优.
1 算法设计
1.1 经验小波变换及其改进
针对经验小波变换[11]需预先设置分解个数、在极值点干扰下信号频段划分不恰当的问题,做如下改进,得到改进经验小波变换(improve empirical wavelet transform,IEWT).
1) 对输入信号f(n)进行傅里叶变换,得到傅里叶频谱.
2) 用顺序统计滤波包络法[12]中的最大值滤波器计算傅里叶频谱包络线.
3) 使用大津算法[13]对频谱进行自适应阈值提取,将频谱划分为两段,第一段为前景,第二段为背景.当两段的类间方差达到最大值时,将其定义为频谱阈值T.利用T对包络线进行修正,大于T的部分保持不变,小于T的部分直接置0.
4) 采用高斯加权移动平均滤波器对频谱包络线进行平滑处理,去除包络线中的平顶部分,使包络线变得平滑,不存在一阶不可导点.
5) 统计局部极大值个数,将其设置为要分解经验小波分量(empirical wavelet function,EWF)的个数.定位两个局部极大值中间局部极小值的位置,并将其位置频率按升序排序,作为频谱划分的依据.
6) 在每个频段内构造经验尺度函数和经验小波函数,后续处理与普通EWT一致,公式见文献[11].
1.2 K-L散度
K-L(Kullback-Leibler)散度[14]可定义为

(1)
其中:P代表原始样本;Q表示经过IEWT分解后的经验小波函数组;Q(i)是其中的第i个EWF.
K-L散度值越小,表明两个信号关系越近,该分量是信号的有效成分;反之,则是信号的干扰成分.振动信号经过分解后,解析出有效成分和一些无效的直流、噪声分量.通过比较分解后信号与原始信号间关系的远近,选取出较佳的分量,达到剔除无效成分的目的.
1.3 堆栈自编码器
SAE[9]由多个自编码器(auto-encoder,AE)堆叠而成.采用SAE进行分类的步骤为:
1) 训练第1个AE.通过编码器提取特征,再通过解码器重构输入向量,当输入和输出达到最小重构误差时,即完成AE的训练,获得网络的权重和偏差.此过程中采用的损失函数为:
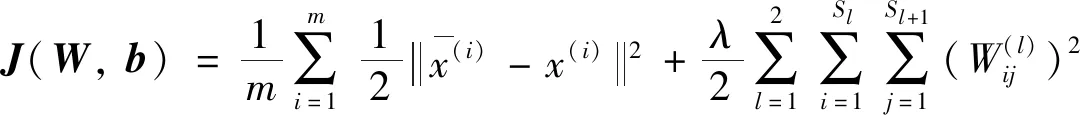
(2)
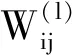
2) 将上一个AE的低维输出向量作为下一个AE的输入,利用步骤1) 的方法完成其余AE的训练.
3) 堆叠各AE编码部分,将前一层输出的特征作为下一层输入,构成特征逐层压缩提炼的SAE网络.
4)利用带标签数据对误差进行反向传播来更新整个网络参数,实现对SAE网络参数的微调.
首先利用前期初步训练获得的各层权重和偏差,计算各个节点的残差:
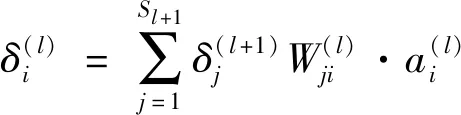
(3)

其次,利用残差计算权重和偏差的改变值,如下式所示,逐层对其进行反向更新,即可完成微调.

(4)
式中:μ为微调学习率.
5) SAE训练完成后通过Softmax分类层完成分类.
SAE模型训练过程中,存在预训练学习率(λ)和微调训练学习率(μ)两个参数需要设定.λ的大小将影响预训练产生的权重及偏差,μ决定目标函数是否能快速地收敛到局部最小值,二者对整个模型的训练具有关键作用,而手动调参繁琐且可能无法找到最优值.为了寻找到合适的参数值,本算法使用带启发式的SSA实现这两个参数的寻优.
1.4 樽海鞘群算法及其优化SAE过程
樽海鞘群算法(SSA)通过模拟樽海鞘的觅食和运动行为建立一种启发式模型,以解决优化问题[10].在参数寻优过程中,领导者带领着追随者在空间中移动并寻找食物,进行全局寻优;追随者利用自身的自由性进行局部探索,减少陷入局部最优的情况.SSA的主控制参数仅有1个,易调节,可避免传统启发式寻优算法因参数调节不当而找不到最优值的问题.在本应用中,实现步骤如下:
1) 初始化SSA参数,如种群规模、初始迭代次数、最大迭代次数等参数,设置种群的初始位置.
2) 初始化SAE两个参数的初始值及寻优范围[bl,j,bu,j],bl,j为参数寻优的下限,bu,j为上限.
3) SSA算法对SAE的参数进行寻优,领导者和追随者的位置更新利用下式完成,
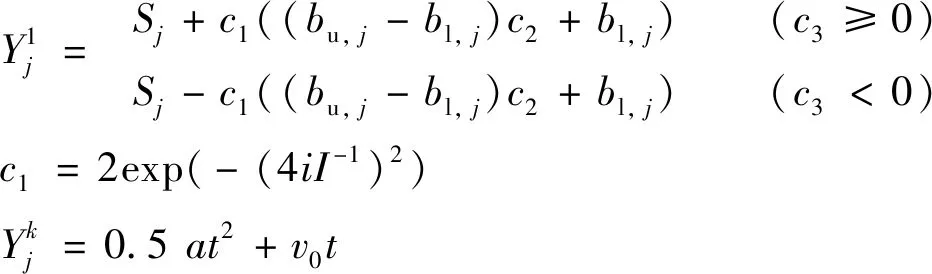
(5)
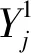
4) 在相应参数值下利用1.3节中SAE训练方法训练分类器模型.
5) 计算各组参数对应的分类器模型的目标函数值,更新并保留目前最优的目标值函数.
6) 判断寻优结果是否满足结束条件(测试集分类准确率达到期望值或达到最大迭代次数),若是,则保留当前最优参数并退出寻优过程;否则,返回步骤3继续迭代,直到满足条件.
2 配电变压器故障诊断模型
1) 采集变压器振动信号,构建变压器多状态样本数据库,并按比例随机分成训练集和测试集.
2) 采用IEWT对样本进行分解,获得一组经验小波分量.
3) 计算每个EWF与原始样本的K-L散度,选散度值较小的前n阶分量构成该样本的有效成分分量.
4) 将所有训练集样本(数量为N)所提取的有效成分分量聚合成输入矩阵X(维度为N× (x×n),其中x是单个样本的数据长度),并给每个样本打上对应的标签,生成标签矩阵Y(维度为1 ×N).
5) 用X和Y训练SAE诊断模型,此过程包括模型的预训练、模型微调整、SSA寻优确立模型参数,具体步骤可见1.4节.
6) 最后用测试集评估模型辨识精度.
3 实验结果与分析
3.1 实验装置及信号采集

图1 实验装置图Fig.1 Experimental device
选用油浸式10 kV变压器(S11-M-315/10)作为研究对象,实验装置如图1所示.振动信号采集装置包含NI-USB6212采集模块和LC0156A加速度传感器(量程为0~±3 g,灵敏度为1.491 Vg-1).文献[15]指出,油浸式变压器最佳的测量位置位于低压侧中部.为此,将传感器通过磁铁吸附在图1的2位置.实验中采样频率为1 kHz,采样时间窗口为0.7 s,每个样本包含了700个数据点.实验数据均从广东省某变压器厂实测获得,主要模拟的变压器运行状态包括正常运行、铁芯两点接地、绕组螺丝松动、绕组变形等4种,分别称为类1~类4,实验过程参考文献[9].4种状态各采集200个样本,总实验样本为800个.
3.2 IEWT分解结果分析
图2为一组变压器振动信号的原始波形.从图中可以发现,绕组变形时波形的幅值较小,形状接近于正弦波,与其他3种状态存在较大的差异;其余3种状态的波形幅值和形状都相近,肉眼难以分辨.此外,原始波形中包含了大量干扰成分,仅从时域波形无法看出信号特征.因此需要对信号进行分解,剔除无用成分,并从时域、频域等不同角度来提取特征.
图3为经IEWT分解后得到的傅里叶频谱及频带划分图.从图中可见,在0 Hz处,每个信号频谱都有较大的能量分布,说明不同运行状态的振动信号频谱中存在较大的直流分量,原因在于传感器自身测量误差和测量操作方式不同造成随机误差,与变压器自身运行状态无关.
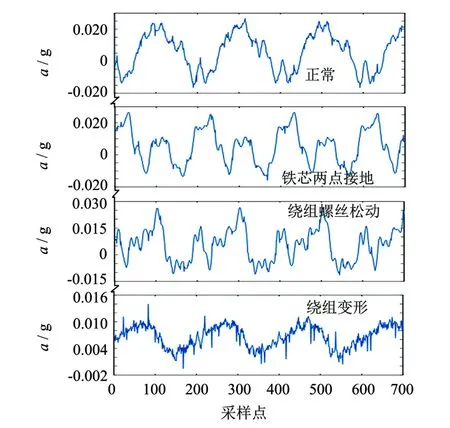
图2 各状态类别的原始波形图Fig.2 Original waveform of each category

图3 各状态类别的频谱分割图Fig.3 Spectrum segmentation results of all categories
从图中还可以看出,除去直流分量,信号在不同频带的幅值变化明显.IEWT可以根据信号自身特性自适应设置分解个数并划分频段,因此各信号的频带划分的范围和个数都不尽相同.这很好地避免了由于分解个数设置过少导致的分解不充分,以及分解个数设置过多导致过度分解问题.在100 Hz基频处,不同状态的信号都有能量分布,其中正常时最大,而异常时倍频分量,如200、300 Hz等频率分布处的能量会有所增加.相比于原始波形,经IEWT分解后4种信号间的区别较大,表达更为直观.
3.3 K-L散度值分析
为了剔除振动信号中包含的直流分量、噪声等干扰成分,同时考虑减少计算量,利用K-L散度来筛选有效分量.不同类别的振动信号经IEWT分解后各分量与原信号之间的K-L散度值列于表1中.从表中可以看出,4种类别样本的EWF2分量与原信号的K-L散度值最小,而EWF1的散度值最大.这说明EWF2与原信号的关系最近,是有效成分;EWF1与原信号关系最远,是无用成分.

表1 各类别样本的K-L散度值Tab.1 K-L divergence value of each category sample

表2 重构信号与原信号相似度值Tab.2 Similarities of reconstructed signal and original signal (%)
对于类4,即绕组变形,IEWT分解的分量个数为4,剔除含直流等干扰成分的EWF1,剩余3个分量.因此,选取K-L散度值较低的前1~3阶分量进行重构.重构信号与原信号的相似程度如表2所示.
当使用前1阶有效分量进行重构时,类2(两点接地状态)和类3(绕组螺丝松动状态)的相似度较低,只有78.25%和62.24%,不足以表征原信号.而使用前3阶分量进行重构时,每个类别的相似度均达到了95%以上,足以表征原信号.因此,选取K-L散度值较低的前3阶分量作为特征.
3.4 SSA寻优分析
将所有的样本经特征提取后,按3∶1的比例随机分成训练集和测试集,即600个训练样本,200个测试样本.训练集样本输入到一个7层SAE(结构为700-600-500-250-100-50-4)进行特征的二次挖掘,并训练一个具有4分类的分类器,此过程利用SSA进行参数寻优.
将预训练学习率和微调学习率设为待寻优参数,即x1和x2,寻优范围为[0,1],迭代次数为20,以训练集分类错误率为目标函数,寻优过程及结果如图4所示.
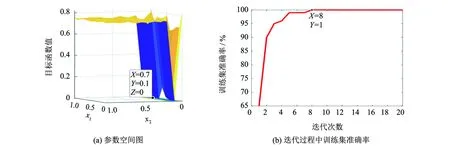
图4 寻优过程及结果Fig.4 Optimization process and result
图4(a)展示寻优过程中目标函数值在参数空间中的变化,最低点是目标函数的最小值,在图中用黑点标注.此时分类错误率为0%,对应的x1和x2分别为0.7和0.1.图4(b)展示寻优过程中训练集的分类准确率.可以看出,迭代一次后准确率达65%;再次迭代后准确率可达90%~96%;经过5次迭代,准确率可保持在99%;迭代8次后,准确率达100%,此时目标函数为0,为最优值,将此最优模型保存.
3.5 分类结果分析

图5 测试集分类结果Fig.5 Classification results of test set
测试集共有200个样本,各个类别的样本数量是随机的,将其输入到训练好的模型中进行验证,其分类结果的混淆矩阵如图5所示.图5中仅有1个样本出现误判,测试集的分类准确率可达99.50%,充分验证了本故障诊断算法的有效性.
图5中最后一行的前4个量表示分类准确率,类别1总共有59个,其中58个预测为类别1,有1个错误的预测为类别2,分类准确率为98.31%,其余3类的分类准确率都为100%.通过查看该错判样本的原始波形及频谱图发现,该样本的频谱图和铁芯两点接地状态十分相似,相应频率处的能量分布更接近铁芯两点接地状态,这与该样本取自于刚上电时刻,铁芯环流较小,谐波含量不大有关.
最后一列的前4个量表示分类精准率,即每个类别分类结果中正确分类的占比.由于存在1个类别1样本误判为类别2,导致类别2的分类精准率下降,但也达到了97.83%,其余3类的分类精准率都为100%.
3.6 对比实验分析
表3 不同方法对比结果Tab.3 Comparison results of different approaches
为了验证算法性能,与文献[8]和[9]中的方法进行比较,结果如表3所示.相比于其他两种方法,本方法的分类准确率更高,尽管训练时间长,但测试时间适中,且与文献[8]的结果差异不大.这里的训练时间指利用训练集样本训练模型需要的时间,测试时间指辨识1个测试集样本所花费的时间.它们是在具有i7-5500U的CPU、4 GB内存和Intel (R) HD Graphics 550集成显卡的运行环境中计算获得.文献[8]数据分解后直接提取多尺度熵进行故障辨识,不需要迭代训练网络,所以花费的时间较少;本方法采用SSA参数寻优,且训练1个7层的SAE花费时间较长,但当训练完成后,调用模型进行测试是十分迅速的;而文献[9]要训练1个4层的SAE和随机森林分类器模型,其训练和测试过程都相对比较漫长.
受仪器精度限制和环境的影响,振动信号通常含有一定量噪声,随着噪声强度的增加,诊断算法的误判可能性会增加.将具有不同信噪比(SNR)的高斯白噪声添加到测试集数据中[16],进一步研判3种方法的抗干扰能力和可靠性,结果如表4所示.所添加噪声的强度通过调整信噪比来控制[17].

表4 抗干扰实验结果Tab.4 Results of anti-interference experiment
表4表明,当SNR从50 dB变化到10 dB时,本方法分类准确率从99.5%降为98.0%,仅降低了1.5%,说明本方法的抗干扰能力出色.这得益于本方法通过IEWT分解出不同频率的信号分量,并应用K-L散度剔除直流和噪声等干扰成分,使得其在强噪声环境下依然具有很强的可靠性.文献[9]的抗干扰性最差,SNR在30~50 dB之间准确率高于86.0%,当SNR降到20 dB或10 dB时,其准确率大大降低.
4 结语
对配电变压器渐变性、潜伏性故障进行诊断是近年的研究热点.基于此,本研究通过采集振动信号构建IEWT-SAE算法对配电变压器运行状态进行监测,进而实现潜伏性故障诊断.经对比分析,结果表明:该方法分类准确率可达99.5%,明显高于文中的对比方法;单个样本的诊断时间为0.181 s,满足现场诊断需求;同时还具有强抗干扰性、自适应特征学习及参数寻优等特点,大大减少人为因素干扰.
