广义绝对值方程的区间算法

王爱祥

（1.中国矿业大学 数学学院，江苏 徐州 221008；2.常州工学院 航空与机械工程学院，江苏 常州 213032）

0 引言

考虑如下形式的广义绝对值方程：

绝对值方程（1）和（2）引起了许多学者的关注.不仅因为其简单和特殊的结构，还因为它可以作为研究线性规划、二次规划、双矩阵对策等优化问题的统一研究框架[1].近年来，绝对值方程（1）和（2）的研究集中在解的存在条件和求解算法上.在理论方面，研究了绝对值方程和线性互补问题的等价性[2]、可解性[3，4]、求解的复杂性[5]等；在算法方面，当绝对值方程存在唯一解时，提出了求解的逐次线性规划法[6]、牛顿型迭代法[7]、投影梯度法[8]和智能算法[9]等.

然而，仍有一些问题值得考虑.调查发现，目前较少有文献研究算法的近似解与绝对值方程的精确解之间的误差界.而两者在实际计算中是否接近是很重要的.可以看下面的例子.

例1考虑广义绝对值方程

容易检验，x*=（1，1）T是这个方程的准确解.但对于近似解，常用的检验标准是范数充分小.但若=（2，0）T，虽有=2.236×10-11，却并不能说明近似解和准确解x*充分接近.基于此，本研究的目的是建立数值稳定的求解广义绝对值方程的算法.

首先简要列举需要用到区间数学的基本概念和符号.对于任意区间定义中点、宽度和绝对值分别为

类似地，n×n的区间矩阵的中点、宽度和范数分别表示为

引理1[10]设A是一个n×n区间矩阵，X是n维区间向量，则.

定义1如果函数f（x）和区间函数F（x）满足F（x）=f（x），f（x）F（x），∀xX则称F（x）为的f（x）区间扩张.

有关区间数学的其他概念和内容可参见文献[10].

1 初始含解区间

在建立区间算法之前，首先构造含有广义绝对值方程准确解的区间.通篇用In表示n阶单位矩阵.对于矩阵A，用|A|表示矩阵A的所有元素取绝对值.λ（A）、ρ（A）和‖A‖分别表示矩阵A的特征值、谱半径和范数.

引理211]对于矩阵ARn×n，则ρ（A）＜‖A‖.

引理3[11]如果矩阵ARn×n满足ρ（A）＜1，那么

引理4[4]如果矩阵A是非奇异的且ρ（|A-1B|）＜1，那么对于任意bRn，广义绝对值方程（1）有唯一解.

定理1如果矩阵A是非奇异的且‖A-1B‖＜1，那么对于任意bRn，广义绝对值方程（1）有唯一解.

证明由引理2知，矩阵A是非奇异的且‖A-1B‖＜1，就有ρ（|A-1B|）＜‖|A-1B|‖=‖A-1B‖＜1.

定理2如果矩阵A是非奇异的且‖A-1B‖＜1.记x*是广义绝对值方程的唯一解，则

式中：⊿=（In-|A-1B|）-1|A-1B||A-1b|.

证明广义绝对值方程等价于x-A-1b=A-1B|x|.进一步，可以得到|x-A-1b|≤|A-1B||x|≤|A-1b||x-A-1b|+|A-1B||A-1b|，于是，（In-|A-1B|）|x-A-1b|≤|A-1B||A-1b|.由引理1得ρ（|A-1B|）＜1.那么，In-|A-1B|是非奇异矩阵.由引理2得到，（In-|A-1B|）-1=≥0.从而有：|x-A-1b|≤（In-|A-1B|）-1|A-1B||A-1b|.

记⊿=（In-|A-1B|）-1|A-1B||A-1b|，则|x-A-1b|≤⊿，即.证毕.

2 区间算法及其收敛性分析

定义映射f：D⊂Rn→Rn，

显然，f（x）的零点恰是广义绝对值方程（1）的根.f（x）的自然区间扩张为

假设矩阵A可逆，定义映射g（x）=x-A-1f（x）=A-1B|x|+A-1b.显然，f（x）的零点是g（x）的不动点.对于区间向量X，g（x）的中值型区间扩张为G（X）=g[m（X）]+G（′X）[X-m（X）]，G（′X）=A-1BD（X）.

定理3设x*为广义绝对值方程（1）的解，且x*X，那么x*G（X）.

证明对于任意向量xX，由泰勒公式得g（x）=g m（X）[ ]+A-1B·∂|ξ|（ξ-x）g m（X）[ ]+A-1B·D（X）[X-m（X）]=G（X），于是，（fx*）=0且x*=g（x*）.即x*=g（x*）G（X）.证毕.

推论1若X∩G（X）=Ø，则广义绝对值方程（1）在区间X中不存在解.

证明由定理1易知，若广义绝对值方程在X中存在解x*，则x*X∩G（X），与条件矛盾.证毕.

推论2若G（X）⊆X，则广义绝对值方程（1）在区间X中至少存在一个解.

证明由定理1知，G（X）⊆X说明g（x）把区间X映射到X本身.又g（x）是连续映射且X是闭凸集，由Brouwer不动点定理知，g（x）在区间X中至少有一个不动点，即f（x）在X中至少有一个零点.证毕.由此，可以构造区间迭代算法.

算法1

步骤1：由（3）式计算初始含解的区间，记为X（0）.设定ε＞0.

步骤3：如果w（X（k+1））≤ε，输出m（X（k+1））.否则，转步骤2.

定理4若矩阵A是非奇异的且‖A-1B‖＜1，则算法1产生的迭代序列{X（k）}满足：

证明由定理2知，f（x）在X上有唯一解，设其为x*.

1）由定理1知，x*X（0）∩G（X（0）），即x*X（1）.假设x*X（k），则x*G（X（k）），故x*X（k+1）.由归纳法，对一切的正整数k，成立x*X（k），且X（k）⊆X（k-1）⊆…⊆X（0）.于是算法得到区间向量序列{X（k）}，且w（X（k+1））≤m（X（k））.根据D（X）的定义知：‖D（X）‖=1.记q=‖A-1BD（X）‖，则q≤‖A-1B‖‖D（X）‖＜1.由引理2知，w（X（k+1））=w{G（′X）[X-m（X）]}≤‖A-1BD（X）‖w（X（k））=q·w（X（k））.

于是，w（X（k+1））≤q·w（X（k））≤q（k+1）·w（X（0））.从而

2）根据算法1，易知X（k+1）⊆X（k）且‖m（X（k+1））-m（X（k））.于是，任取p＞k（p是正整数），有

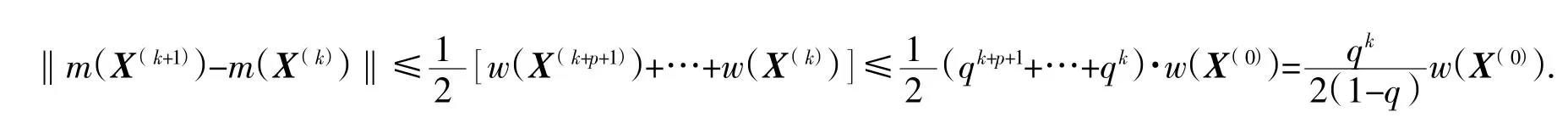
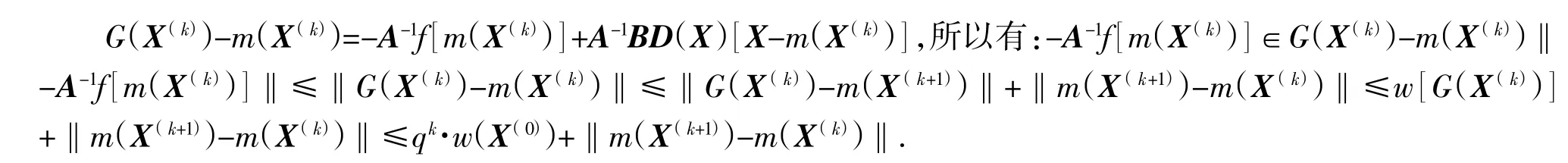
定理4不仅证明了算法的收敛性，还给出了每步迭代中近似解和准确解的误差关系.此外也说明了该区间算法收敛速度至少是线性的.为减少计算量，提高计算效率，利用点迭代来代替区间迭代.

定理5设算法1产生的迭代序列为{X（k）}.以任意x0X（0）为初值，点迭代xk+1=A-1B|xk|+A-1b（k=0，1，2，…）生成序列{xk}.该点序列{xk}收敛到广义绝对值方程（1）的解x*，且|xk-x*|≤βkw（X（0）），其中q=‖A-1B‖.

证明用归纳法证明.当任意点x0X（0），有xkXk，k=0，1，2，….当k=0时，成立.

假设k=m（m≥0），xmXm，有xm+1=A-1B|xm|+A-1bG（X（m））.也就是：xm+1G（X（m））∩X（m）=X（m+1）.由定理3知，由于xk，x*X（k），因此，|xk-x*|≤w（X（k））≤βkw（X（0）），其中q=‖A-1B‖.故当k→∞时，xk→x*.证毕.

定理5说明了虽然用点迭代代替区间迭代，仍然可以同步显示近似解和准确解之间的误差.下面总结点迭代的算法.

算法2

步骤1：由（3）式计算初始含解的区间X.取中点x0=m（X）.设定ε＞0.

步骤2：计算点迭代：xk+1=A-1B|xk|+A-1b，k=0，1，2，….

步骤3：如果‖Axk+1-B|xk+1|-b‖≤ε，输出xk+1.否则，转步骤2.

3 数值测试

为了测试算法的有效性，进行如下的数值实验.程序利用区间程序包Intlab5.4编写，在Matlab平台上实现.计算环境为酷睿i5，2.40 GHz，RAM 16 G.

例2（随机测试）考虑绝对值方程Ax-B|x|-b，其中

容易验证，‖A-1B‖=0.3947＜1.利用（3）式计算，得到含有准确解的区间是

例3[7]（线性互补问题）考虑线性互补问题LCP（M，q），其中M=N+μIRn×n，q=-Mz*且：是单位矩阵.

当m=3时，取μ=1，则‖A-1B‖=0.7553＜1，初始含解区间的最大宽度w（X（0））=57.3492，得到近似解满足：和

为保证得到初始含解区间，设定参数μ=4，选择不同维度n.计算结果见表1，其中n表示问题维数，ERR表示算法得到的近似解和准确解之间误差的欧氏范数，T表示算法的CPU时间，单位为s.

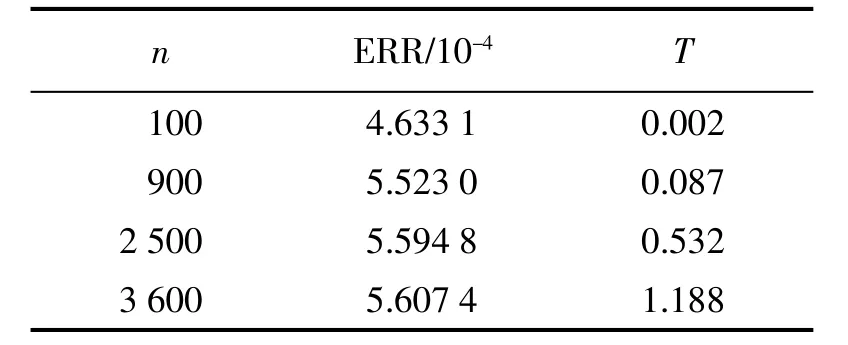
表1 例2的计算结果（μ=4）

4 结论

提出了广义绝对值方程的一类区间型算法.首先得到一个含有准确解的区间，然后用区间迭代的方法去缩小区间，得到准确解.由于区间运算的代价较大，提出用点迭代的方法来代替区间迭代.算例测试也验证了算法的有效性.但是，初始区间的运算涉及到矩阵求逆运算.对于大规模问题，求逆运算代价较大.如何优化初始区间计算，值得进一步考虑.