基于堆叠门控循环单元残差网络的知识追踪模型研究

2022-11-25黄彩蝶王昕萍陈良育刘勇

华东师范大学学报（自然科学版） 2022年6期

黄彩蝶,王昕萍,陈良育,刘勇

（1.华东师范大学软件工程学院,上海 200062;2.华东师范大学基础教育与终身教育发展部,上海 200062）

0 引言

随着大规模开放在线课程(Massive Open Online Course,MOOC)的普及,更多的学生和社会人士加入到了在线教育中.2020 年年初开始的全球新冠肺炎疫情让在线教育呈现出“井喷”态势,越来越多的在线教育品牌出现在人们的视野中,在线教育已成为教育领域的热门趋势.然而在线教育领域也存在一些技术瓶颈,例如,大部分的在线教育都采用直播授课、视频回放和社区交流结合的形式,而这些授课形式很难追踪到每个学生的学习情况.因此,针对学生知识点掌握情况的知识追踪任务就显得格外重要,如何精准地评估学生的知识状态是目前知识追踪领域的关键问题.为了对学生因材施教,实现教育领域和信息领域的融合,智能导学系统(Intelligent Tutoring System,ITS)[1]被提了出来,即借助人工智能技术,让计算机扮演虚拟导师向学习者传授知识,并提供一对一指导的专项服务.知识追踪作为智能导学系统中的关键性问题,其特点是自动化和个性化,其任务是根据学生的历史学习轨迹来自动追踪学生的知识水平随时间的变化过程,以便准确地预测学生在未来学习中的表现,从而为学生提供相应的学习辅导.在这个过程中,知识空间被用来描述学生知识的掌握程度.有教育学研究者认为[2],习题会考察一组特定的、相关联的知识点,学生对于习题所考察的知识点的掌握程度会影响其在习题上的表现,即习题考察是学生认知状态的外显.

多年来,基于循环神经网络(Recurrent Neural Network,RNN)一直是知识追踪方法的主导方法,有以下几点原因: ①基于神经网络(Neural Network,NN)的方法不需要人工选取特征;② 在线教育产生的数据众多,而题目的得分数据是学生知识空间最直接、相关性最强的外显数据,也是平台较为容易获取的数据,所以基于得分数据的神经网络研究方法的通用性更强;③RNN 及其变体的计算结合了过去时间步的输出,即将过去的信息融入当前时刻的计算,所以在知识追踪任务中,这类模型在具有时序性信息的数据集上能够取得较好的效果.

Piech等[3]提出的深度知识追踪(Deep Knowledge Tracing,DKT)模型将RNN 应用于知识追踪任务,在当时达到了最优的效果.但DKT 模型中的RNN 只有很少的层数,这就导致了序列学习容量不高.研究表明,叠加的RNN 可以减轻长期依赖的学习困难问题[4].所以Sha等[5]使用双层堆叠的长短期记忆网络(Long Short-term Memory,LSTM)来扩大序列学习容量,并使用残差连接减小训练难度.由于LSTM 中“门”的引入,导致LSTM 的参数是传统RNN 的4 倍,增加了过拟合的风险;而门控循环单元(Gated Recurrent Unit,GRU)可以以更少的参数达到与LSTM 相当的效果.所以本文提出了一种基于GRU 的残差网络,使用双层堆叠的GRU (Stacked-Gated Recurrent Unit,S-GRU)网络对学生作答序列进行学习,并采用残差连接的方式来降低模型训练的难度.

综上,本文的主要工作: ①提出了双层堆叠GRU 残差(Stacked-Gated Recurrent Unit-Residual,S-GRU-R)网络来处理知识追踪任务,预测学生在下一个时刻的答题正确率,追踪学生知识水平的变化;② 在Statics2011 数据集上进行了实验,并与其他多个模型预测的AUC (Area Under the Curve)和F1-score 进行了对比,结果显示本文提出的模型有更好的预测精度.

本文后续结构: 第1 章介绍相关工作,以对知识追踪任务有宏观的认识;第2 章定义本文要解决的问题;第3 章从模型的输入、网络结构、模型优化目标这3 个部分介绍本文提出的S-GRU-R 模型;第4 章介绍实验详情,包括数据集、评价指标、基线模型、实验细节、结果与分析;第5 章总结全文,并对未来的研究提出展望.

1 相关工作

知识追踪任务从研究方法上可分为3 种: 基于概率图的知识追踪、基于概率矩阵分解的知识追踪和基于深度学习的知识追踪[6].

1.1 基于概率图的知识追踪

贝叶斯知识追踪(Bayesin Knowledge Tracing,BKT)[7]模型是基于概率图模型的典型模型之一.该模型用1 组二元变量来建模学生的知识空间特征,每个变量代表学生是否掌握某种知识点;随着学生做题数量的增加,它通过隐马尔可夫模型(Hidden Markov Model,HMM)来维护代表知识点熟练度的二元变量[8].后来又有许多研究针对BKT 模型的不足提出了一些新的模型,从不同角度弥补BKT模型的缺点和不足,例如: 针对原始BKT 模型,假设学生不会遗忘已经学会的知识,Baker等[9]将猜测和失误加入到BKT 模型中进行预测,提升了预测的准确性;Pardos等[10]将个体的先验知识加入BKT 模型,以提高预测精度.以BKT 模型为代表的基于概率图的模型很好地运用了教育学理论,可解释性强;但是其预测效率极大程度上取决于概率图建立的合理性,当概率图建立不够合理时,其预测性能就会大幅度下降[6].

1.2 基于概率矩阵分解的知识追踪

概率矩阵分解(Probabilistic Matrix Factorization,PMF)[11]是推荐系统领域的经典算法.Chen等[12]提出的KPT (Knowledge Proficiency Tracing,KPT)模型通过教育先验来追踪学生的知识空间水平,该模型除了将HMM 引入使其可以根据时间调整学生知识点掌握矩阵外,还将记忆和遗忘理论融入到U(用户知识掌握程度的张量)的变化中.PMF 模型能够更好地利用题目包含的知识点信息,且可以利用Q矩阵(专家标记题目–知识点矩阵)较好地提升模型的预测效果,还能直观地反映学生知识点的掌握情况.但PMF 模型的可扩展性较差,难以加入除了题目知识点以外的其他相关信息,如题目文本、题目难度、学生的隐性反馈(做题停留时间)等[6].

1.3 基于深度学习的知识追踪

Piech等[3]提出的DKT 模型是深度知识追踪领域的基本模型,它是以RNN 模型为基础结构.由于RNN 模型是一种具有记忆性的序列模型,而序列结构不仅使其符合学习中的近因效应,并且保留了学习轨迹信息[13],所以RNN 模型及其变体成为深度知识追踪领域使用最广泛的模型,DKT 模型也成为了将深度学习应用于知识追踪的开山之作.尽管DKT 模型的预测性能优于当时的经典方法,但是DKT 模型缺乏深入分析知识交互的过程[14],具有可解释性差的弱点;DKT 模型有RNN 长期依赖的问题;另外,DKT 模型的输入为one-hot 编码的学生交互序列,输入类型单一,导致学习特征少,这也是DKT 的缺点之一.所以,可解释性差、长期依赖问题和学习特征少成为DKT 的3 个最显著的问题[15].许多研究者为了解决这3 个显著问题,对DKT 进行了深入研究,并提出了很多新的方法,例如:

(1) 针对可解释性差的问题,Dong等[16]在A-DKT 模型中使用Jaccard 系数计算知识成分之间的注意力权重,并结合LSTM和总注意力值得到最终的预测结果;Zhang等[17]提出了结合外部记忆模块与RNN 的动态键值对的记忆网络(Dynamic Key Value Memory Networks,DKVMN)模型,DKVMN 在RNN 的基础上加入了MANN (Memory-Augmented Neural Network)思想,用1 个静态矩阵存储配合1 个动态矩阵存储来更新学生的知识状态,提高了预测效果;Ai 等[18]进一步扩展了DKVMN 模型,使其支持人工标注的知识成分信息.

(2) 为解决长期依赖问题,Abdelrahamn等[19]使用Hop-LSTM 进一步扩大了LSTM 的序列学习容量,可以根据隐藏单元之间的相关性进行跳跃连接;还有研究指出,RNN 的层层叠加可以减轻LSTM 中长期依赖关系的学习困难问题[4],基于这个结论,Sha等[5]提出了一种双层堆叠LSTM 残差模型,简称NKT (Neural Knowledge Tracing)模型,该模型设计了一种双层堆叠的LSTM,并使用残差连接减小训练难度,实验证明,这种叠加的LSTM 可以有效地扩大序列学习的容量;Pandey等[20]提出的SAKT (Self-Attentive Knowledge Tracing)模型,首次将Transformer 模型应用于知识追踪领域;Choi等[21]提出了SAINT(Separated Self-AttentIve Neural Knowledge Tracing)模型,来解决SAKT模型的注意力层太浅和Q,K,V矩阵计算方法缺乏经验支持等问题;Pu等[22]改进了Transformer 的结构,在其中加入题目的结构信息和答题的时间信息.

(3) 针对缺少学习特征这个问题,Zhang等[23]采用特征工程的方式,将答题时间、答题次数和第一次动作(首先尝试解答还是直接寻求帮助)使用自动编码器(auto-encoder)降维后加入到LSTM 的输入层中;Nagatani等[24]在DKT 模型中加入遗忘特征;Cheng等[25]在其模型AKT (Adaptive Knowledge Tracing)中使用与EERNN (Exercise-Enhanced Recurrent Neural Network)模型相同的文本特征提取方法,并加入学生的猜测和失误行为特征;Tong等[26]在其EHFKT (Exercise Hierarchical Feature Enhanced Knowledge Tracing)模型中使用BERT (Bidirectional Encoder Representation from Transformers),从题目文本中提取出知识分布、语义特征和题目难度等有用信息.总地来说,相比其他两类方法,基于深度学习的知识追踪模型还是目前的主流方法.

2 问题定义

知识追踪任务是根据学生的做题信息对学生的知识掌握水平进行跟踪,对学生的未来表现进行预测.本文的模型输入可以表示为

假设有N个学生,每个学生答题数目为M,D代表数据集,Si={xi1,xi2,···,xit}为学生做题序列,在t时刻,xit包含两部分内容: ①当前时刻学生正在回答的知识点问题qit;② 学习者对该问题的回答情况ait(正确或错误),其中ait={0,1},0 表示学生回答错误,1 表示学生回答正确.将学生行为序列经过编码后输入RNN 进行训练,然后通过预测输出层得到学习者知识掌握水平yit,即预测下一个时刻xi(t+1)学生答题的正确率.正确率范围从0 到1,表示预测概率.

本文的基本任务如下.

(1) 预测学生未来答题表现,即下一个时间步的答题正确率.

(2) 跟踪学生的知识水平变化状态,并以此为依据对学生进行个性化导学.

3 模型介绍

本文使用双层堆叠GRU 残差网络来处理深度知识追踪任务,对传统RNN 进行改进;通过双层GRU 层加残差连接对学生做题序列进行处理,跟踪学生知识水平变化状态,预测学生未来表现.

3.1 模型输入

模型输入的是学生答题结果序列.先将源数据预处理成图1 左边的格式,从上往下的第一行是答题数,第二行是题目ID (Identity Document),第三行是对/错信息(1 为答对,0 为答错);然后将数据按最大时间分割成最小单位(如果答题分割后不足,最大时间步就用0 填充);数据分割后,将输入数据通过one-hot 编码成预处理后的数据进入网络,输入数据的维度为2 倍的知识点数.如图1 所示,设最大时间步为5,题目知识点数为5,某位学生的答题记录为图中左边框内数据所示;将其通过onehot 编码成图中的{0,1}二元格式xi1,xi2,xi3,xi4,xi5;最后将所有编码结果合并成1 项时间序列数据作为这个学生的输入序列xi={xi1,xi2,xi3,xi4,xi5}.

3.2 网络结构

知识追踪任务中的数据具有时序性,所以要求所用的算法能够处理数据中的时序性特征.RNN 及其变体LSTM、GRU 都具有记忆功能,适用于知识追踪任务中的时序性数据.RNN 比普通的神经网络增加了1 个循环机制,即将上一个隐藏层输出结果作为条件加入到当前隐藏层的计算中.其结构如图2 所示.

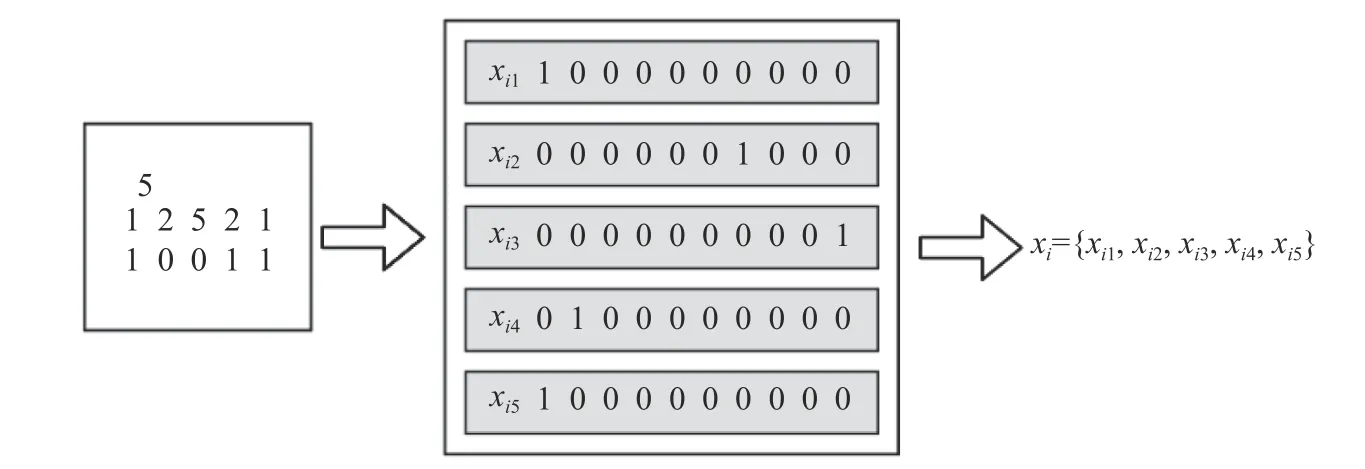
图1 模型输入Fig.1 Input of the model

图2 循环神经网络Fig.2 RNN (recurrent neural network)

RNN 的输入序列Si={xi1,xi2,···,xit}通过隐藏层计算得到序列hi={hi1,hi2,···,hit}和输出序列ki={ki1,ki2,···,kit}(学生的知识水平序列).其对应公式为

式(1)—(2)中:W*为系数(下同);b*为偏移量(下同);σ为激活函数(下同).

学生未来成绩的预测依赖于对学生历史做题时间序列的分析,时间序列越长,学生的知识水平变化越多,序列特征越多,预测的精度相应会更高.但是RNN 的记忆能力只在短时期内有效,对于时间跨度大的依赖则没有效果,当信息积累到一定长度,初始信息对于结果的影响便会消失.为了解决RNN 的长期依赖问题,LSTM 引入了门 (gate) 的概念,通过输入门、输出门、遗忘门来选择或遗忘数据特征,实现对序列中特征长期依赖的捕捉,一定程度上解决了RNN 梯度消失的现象.GRU 又在LSTM 的基础上进行了改进.其网络结构如图3 所示: GRU 只有2 个门,即重置门r和更新门z,去掉了LSTM 中的记忆单元,只通过隐变量h传递数据特征.

GRU 的更新可以分为如下几个步骤.

(1) 重置门:rt表示GRU在t时刻的重置门.其定义为

(2) 更新门:zt表示GRU在t时刻的更新门.其定义为

(3) 新记忆: 更新门zt决定了上一时刻的隐变量对当前时刻影响的大小.新的记忆h′是对新的输入xt和前一时刻隐藏层的输出ht-1重置结果的结合,既包含了当前输入信息,又包含了前一时刻的隐藏层输出信息.其定义为

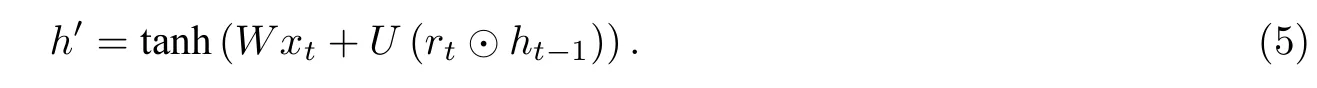
式(5)中:U为系数;⊙代表矩阵中对应元素相乘.

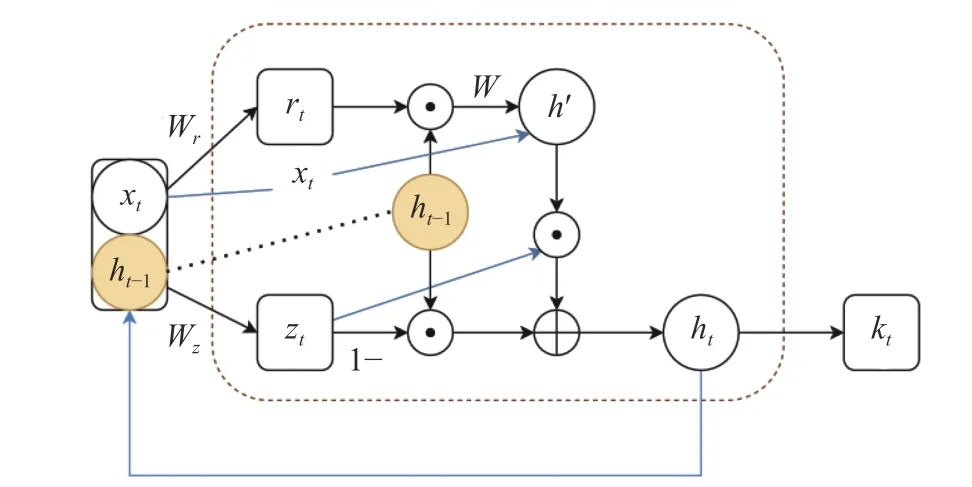
图3 门控循环单元Fig.3 GRU (gated recurrent unit)

(4) 隐藏层:t时刻的GRU 隐藏层状态ht是过去状态ht-1和当前状态h′的有权和,两者的权重由更新门zt控制.其定义为

GRU 只用2 个门同样实现了LSTM 中对长期依赖特征的捕捉,其参数比LSTM 更少,训练更快.

Sha 等[5]针对RNN 长期依赖训练困难的问题,提出了NKT,使用双层堆叠LSTM 模型和残差连接.受上述研究的启发,本文采用双层堆叠的GRU 残差连接网络来克服RNN 中长期依赖训练困难的问题.

本文提出的堆叠GRU 残差(S-GRU-R)网络结构如图4 所示.

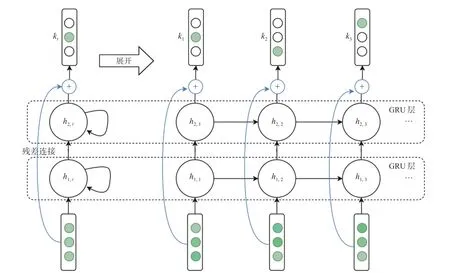
图4 双层堆叠GRU 残差(S-GRU-R)网络结构Fig.4 Structure of the stacked-GRU-residual (S-GRU-R) network

双层堆叠GRU(S-GRU)网络的定义为

由输入xt进入第一层GRU 网络得到隐变量h1,t;再由第一层GRU 网络的输出作为第二层GRU 网络的输入,得到第二层GRU 网络的输出h2,t;然后再由一层全连接层得到知识水平向量kt.

由于RNN 层数的增加会导致模型更难训练[27],所以模型又引入了残差连接[27-28].残差连接的加入可以让堆叠GRU 网络训练更容易.所以本文提出了加入残差连接的堆叠GRU 残差(S-GRU-R)网络.S-GRU-R 网络与S-GRU 网络的区别体现在

其中⊕代表向量拼接.

3.3 模型优化目标

本文通过最小化目标函数(学生答题结果的预测值kt+1(qt)和学生答题真实结果at之间的交叉熵损失函数)来优化各个参数.因为知识追踪任务预测的是下一个时间步的答题情况,所以与at对应的预测值为kt+1(qt).本文使用Adam 方法[29]优化参数,损失函数为

4 实验

4.1 数据集

本文所使用的公共数据集为Statics2011①Statics2011: https://pslcdatashop.web.cmu.edu/DatasetInfo?datasetId=507.该数据集来自一门学院级的工程静力学课程,包含333 个学生在1 223 个知识点上的189 927 条回答记录,平均每个学生回答记录数目为568.

4.2 评价指标

本文使用平均曲线下面积(Area Under the Curve,AUC)和平均F1分数(F1-score,F1)作为评估预测性能的指标.AUC 被定义为ROC (Receiver Operating Characteristic) 曲线与坐标轴围成的面积,AUC 值为50%时,表示随机猜测得到的结果,AUC 值越高,预测性能越好.

在评价体系中,准确率(Precision,P)和召回率(Recall,R)越高,表示算法性能越好.但在一些场景下,准确率和召回率可能是矛盾的,所以使用F1综合评价这2 个指标.相应公式为

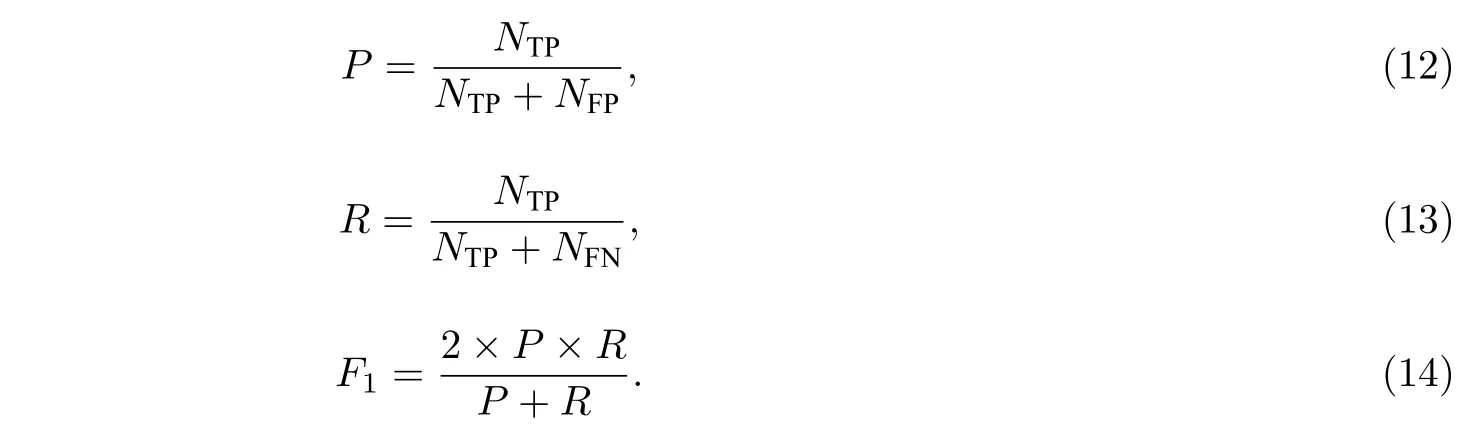
式(12)—(14)中:NTP(True Positive,TP)表示将正类预测为正类的数量;NFP(False Positive,FP)表示将负类预测为正类的数量;NFN(False Negative,FN)表示将正类预测为负类的数量.

对每个模型,本文都进行了20 次测试,取平均AUC 值和平均F1值.

4.3 基线模型

为了对比本文提出的S-GRU-R 模型与其他模型的性能,本文采用了2 种基线模型: 深度知识追踪(DKT)和堆叠LSTM 残差网络(NKT),另外还设置了消融实验S-GRU 模型.模型及其具体参数设置如下.

(1)深度知识追踪(DKT).本文实现了文献[3]中提到的以LSTM 模型为主体网络的方法.模型训练参数设置详情: 初始学习率为0.001,最大时间步为50,最小批次数量为128,学习轮次为100 次,LSTM 隐层维度为200,LSTM 层数为1,优化器选择Adam.

(2)堆叠LSTM 残差模型(NKT).本文实现了文献[5] 提出的双层堆叠LSTM 残差模型.模型训练参数设置详情: 初始学习率为0.001,最大时间步为50,最小批次数量为128,学习轮次为100 次,LSTM 隐层维度为200,LSTM 层数为2,优化器选择Adam.

(3)堆叠GRU (S-GRU)模型.S-GRU 模型采用双层堆叠的GRU 网络进行训练.模型训练参数设置详情: 初始学习率为0.001,最大时间步为50,最小批次数量为128,学习轮次为100 次,GRU 隐层维度为200,GRU 层数为2,优化器选择Adam.

4.4 实验

本文实验在CentOS 7 系统下进行.具体硬件环境: CPU 为i7-9700CPU@3.00 GHz;GPU 为GTX-2080Ti;DDR4 64 GB 内存.开发环境: Python3.7;PyTorch1.8.S-GRU-R 模型使用PyTorch 框架实现,以4∶1 的比例将数据集分为训练集和测试集.优化器选择Adam.

参数设置如表1 所示.

表1 模型参数设置Tab.1 Model parameter settings

4.5 结果与分析

知识追踪的基本任务是预测学生在下一题中的作答正确率和追踪学生知识水平变化.预测任务通过对比模型预测结果与真实结果的误差,比较模型的预测性能;追踪任务通过跟踪学生在某个时间段内知识掌握程度的变化来体现.

4.5.1 预测未来表现

为了评估模型的性能,本文选择深度知识追踪(DKT)和堆叠LSTM 残差网络(NKT)作为基线模型进行对比实验,堆叠GRU(S-GRU)网络作为消融实验,并分别计算每种模型测试的AUC 值和F1值,其中DKT 模型是基于LSTM 实现的.实验结果如表2 所示,其中最优值被加粗.图5 更加清晰地展现了各模型的预测AUC 值在训练过程中的变化.

根据表1和图5 中的数据可以得到以下结论.

(1)本文提出的S-GRU-R 模型的AUC 值明显优于DKT 模型和NKT 模型.

(2) S-GRU-R 模型比S-GRU 模型预测表现更好,在AUC 值和F1上都超过了后者.

(3) S-GRU-R 模型在训练8 个轮次后AUC 值达到峰值,DKT 模型和S-GRU 模型在训练12 个轮次后AUC 值达到峰值,NKT 模型则在训练到20 至40 个轮次阶段达到峰值.因此S-GRU-R 模型比其他模型更快得到最优性能.

表2 模型AUC 值和F1 值对比Tab.2 Comparison of the models’ AUC value and F1 value

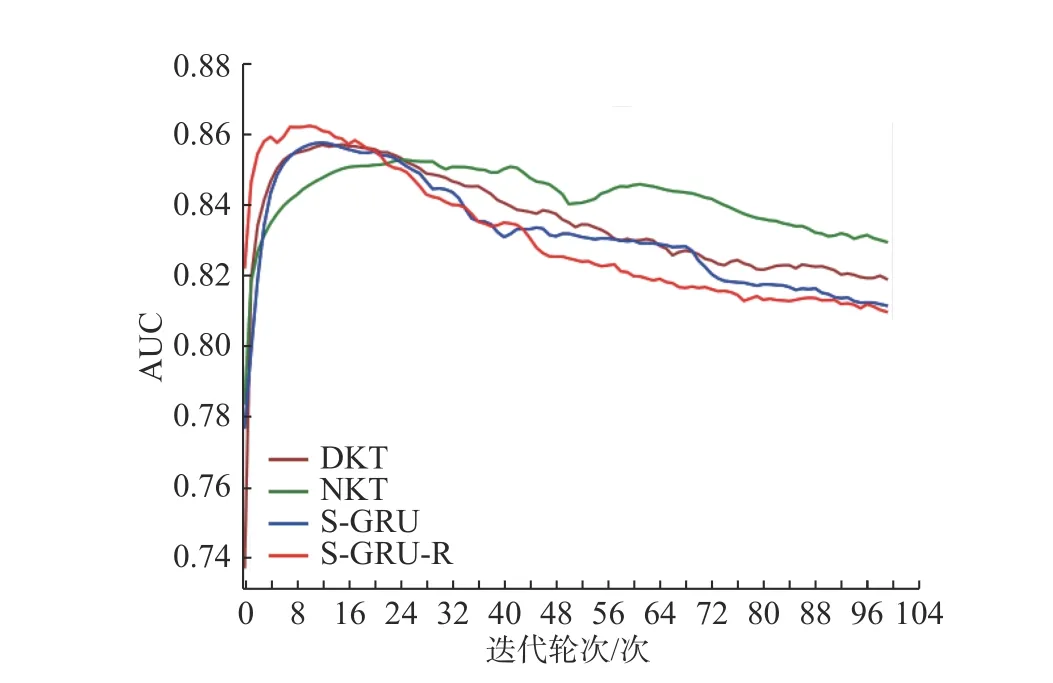
图5 模型AUC 值对比Fig.5 Comparison of the models’ AUC value

4.5.2 追踪知识水平

除了预测学生在下一时刻答题的正确率,知识追踪的另一任务是跟踪学生的知识水平变化.图6显示了S-GRU-R 模型对随机抽取的学生答题记录的知识水平跟踪结果.

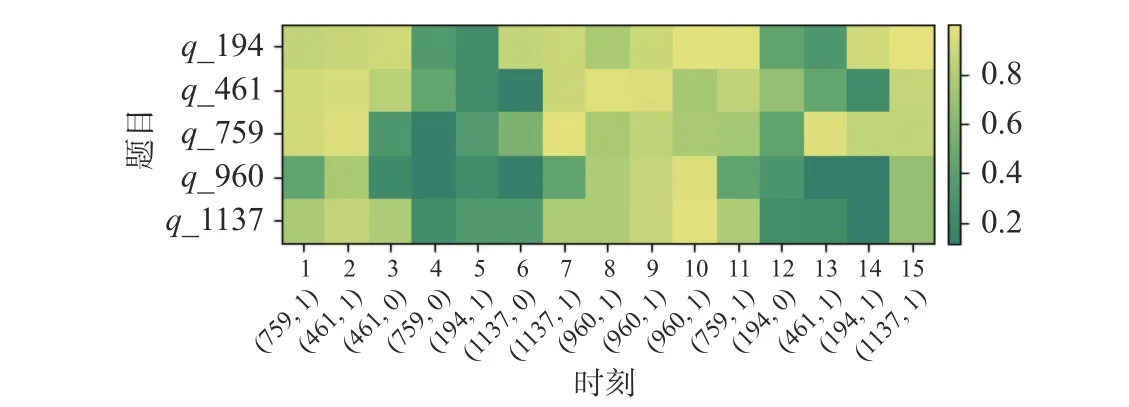
图6 S-GRU-R 模型追踪学生知识水平变化热力图Fig.6 Heat map of students’ knowledge level as tracked by S-GRU-R

图6 中,横轴代表学生答题的时间序列,用1 个二元组来表示学生的答题记录,例如第1 条(时刻1)记录(759,1)代表学生对759 号题目进行作答,作答结果为正确(正确为1,错误为0);纵轴代表学生解答过的题目(q_编号).图中每一个方格颜色的深浅代表了学生在当前时刻的知识掌握程度(范围为0～1): 颜色越深,表明学生对该题对应知识点的掌握越差;颜色越浅,表明该学生对该题对应知识点的掌握越好.模型共追踪了学生在15 个时刻上的知识点能力掌握值.聚焦编号为194 的题目结果,当时刻5 (该学生答对了194 号题目)发生时,结果显示学生在194 号题目上的知识点掌握能力值有上升趋势,即颜色由深变浅;当时刻12 (该学生答错了194 号题目)发生时,结果显示学生在194 号题目上的能力有所下降,所以颜色由浅变深;最后当时刻14 (学生答对了194 号题目)发生时,结果显示学生在194 号题目上能力值又有所提升,即颜色由深变浅.其他题目也有类似效果.

综上所述,当某时刻学生答题情况发生变化时(从正确到错误或从错误到正确),模型可以检测出此时刻学生知识点掌握程度的变化;根据这个变化,可以了解学生的知识空间水平,从而对学生进行个性化导学服务.