一些涉及二重级数的q-同余式

魏传安,余桐

（海南医学院 生物医学信息与工程学院,海口 571199）

0 引言

对任意的复数x,定义移位阶乘为

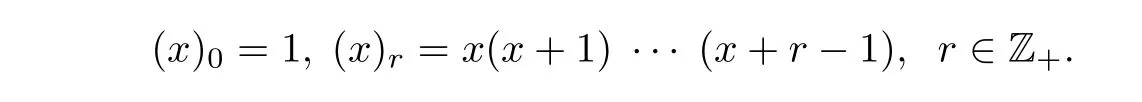
Long[1]提出了一个与二重级数有关的有趣猜想: 设p是任意奇素数,则

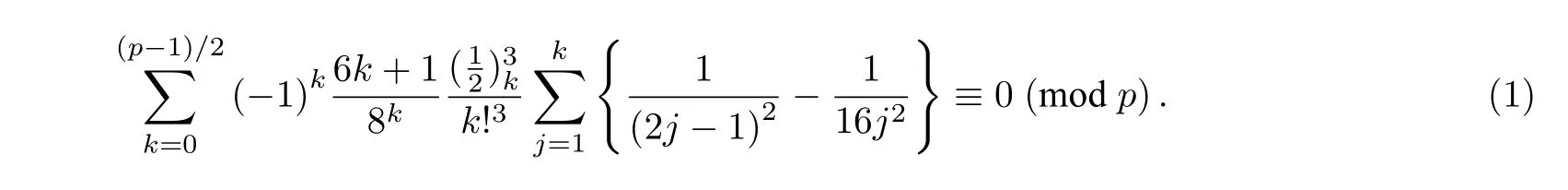
Swisher[2]证明了上述猜想.

设q和x是任意复数.定义q-移位阶乘为

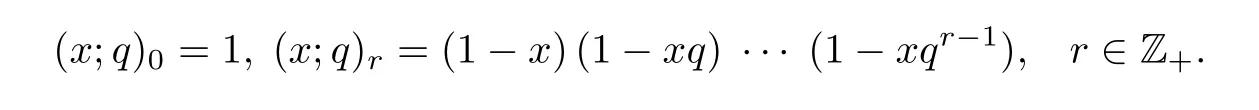
为了方便,有时候也会使用简化符号:

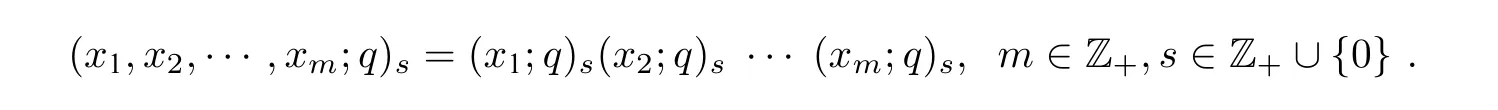
本文用[r]=1+q+q2+···+qr-1表示q-整数,用Φr(q) 表示q的第r阶分圆多项式:

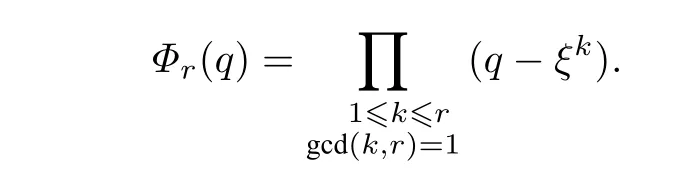
上式中:ξ是一个r次本原单位根.Gu等[3]给出了式(1)的一个q-模拟: 设n是任意的正奇数,于是

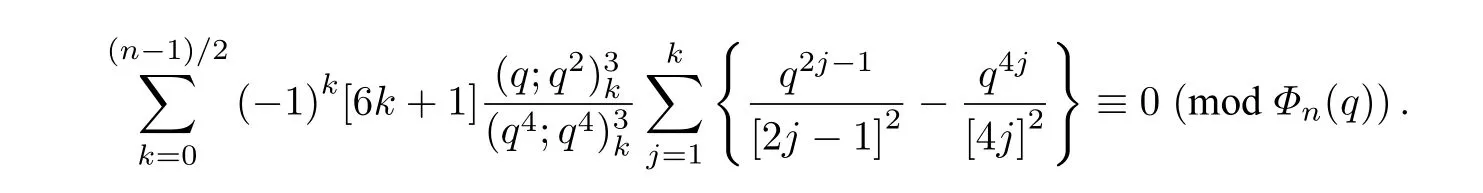
如果读者想了解最近出现的同余关系的q-模拟及相关的技巧,可以参见文献[4-11].

根据Gasper等[12]所提出的方法,可以把q-级数定义成

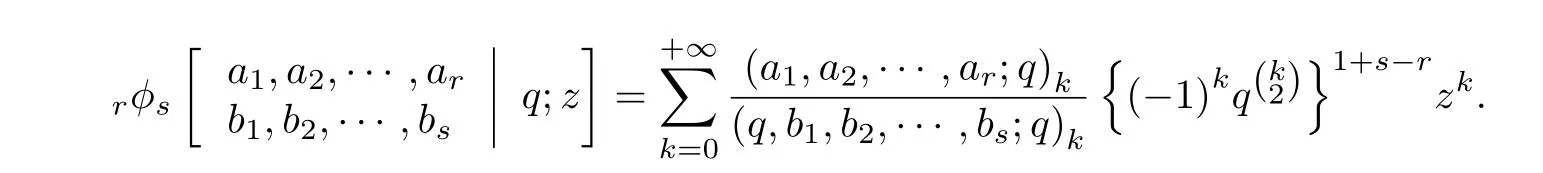
设n是一个非负整数,从而Watson的8ϕ7变换公式[12]可以表达为

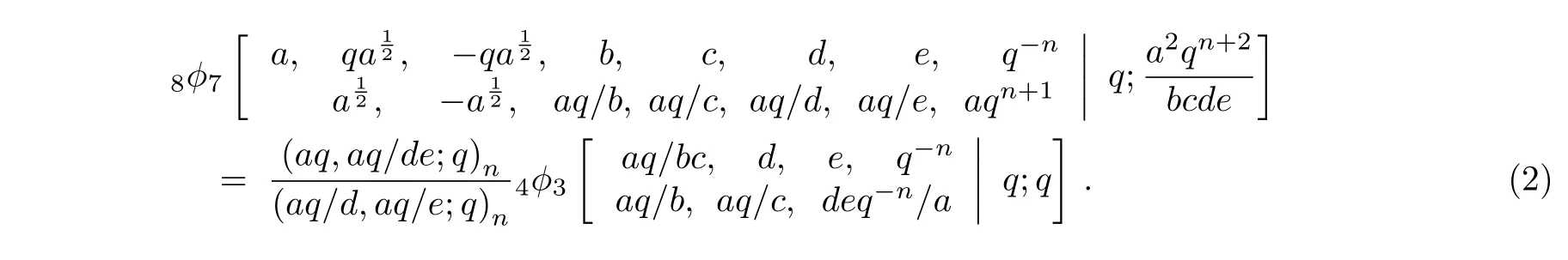
在式(2)中,令b→+∞,则有

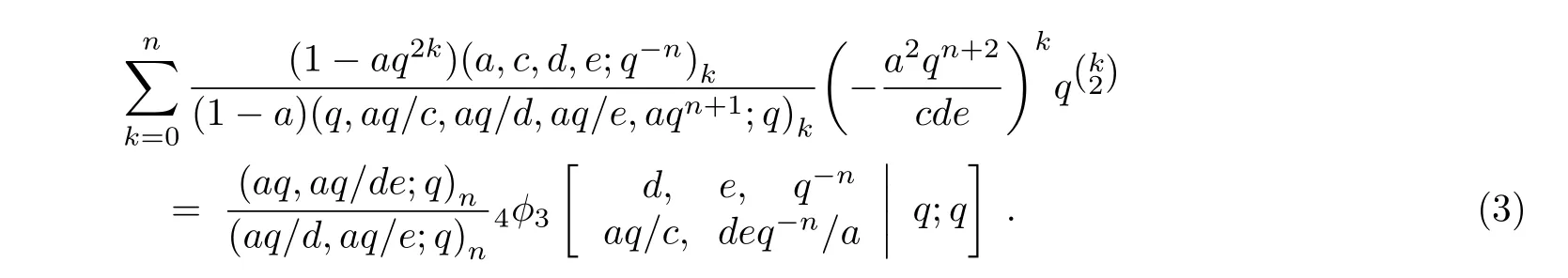
利用式(2)与式(3),本文证明下面3 个定理成立.

定理 1对任意的正奇数n,有

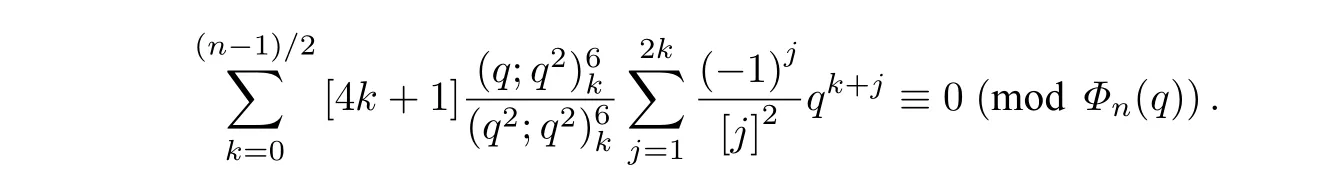
在定理1 中,取n为一个奇素数p,令q→1,则有推论 1 的同余式.

推论 1设p是一个奇素数,则

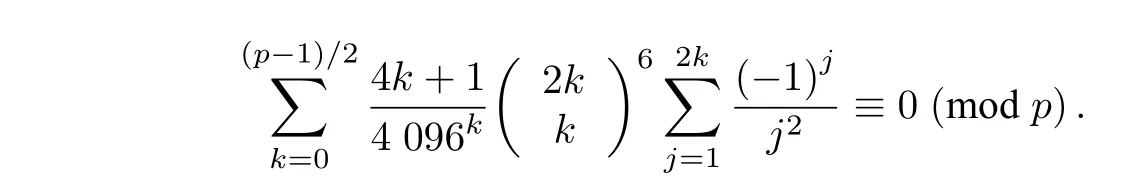
定理 2对任意的正奇数n,有

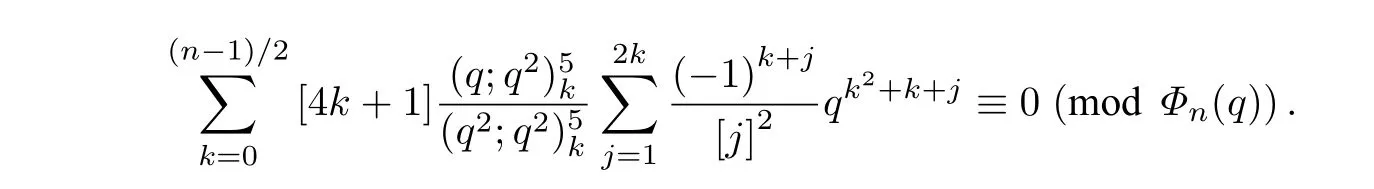
在定理2 中,取n为一个奇素数p,令q→1,则可推导出推论 2.

推论 2设p是一个奇素数,则

定理 3对任意的正奇数n＞1,有

上式中:[n]q2=1+q2+(q2)2+···+(q2)n-1.

在定理3 中,取n为一个奇素数p,令q→1,则可得推论 3.

推论 3设p＞3是素数,则

1 定理1 的证明

对式(2)进行参数变换:

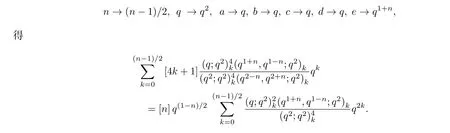
之后,可以继续下面的计算过程:

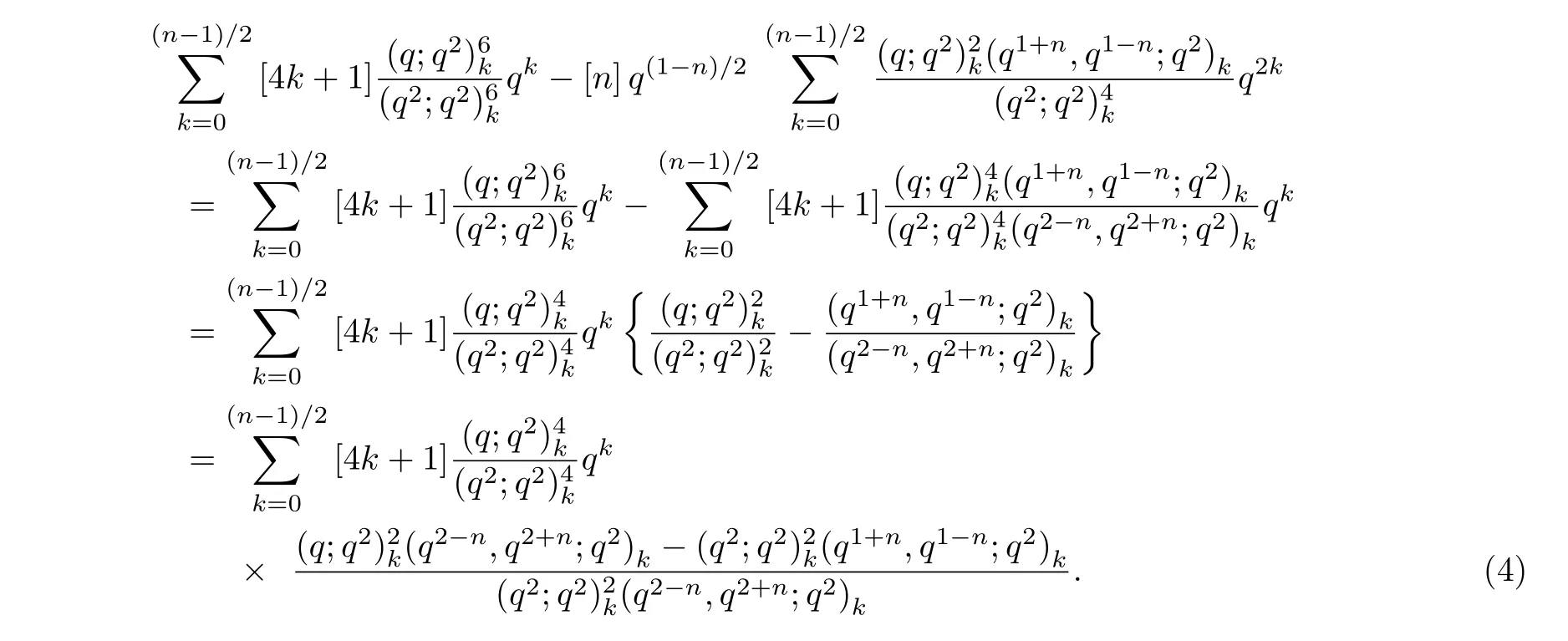
通过关系式:

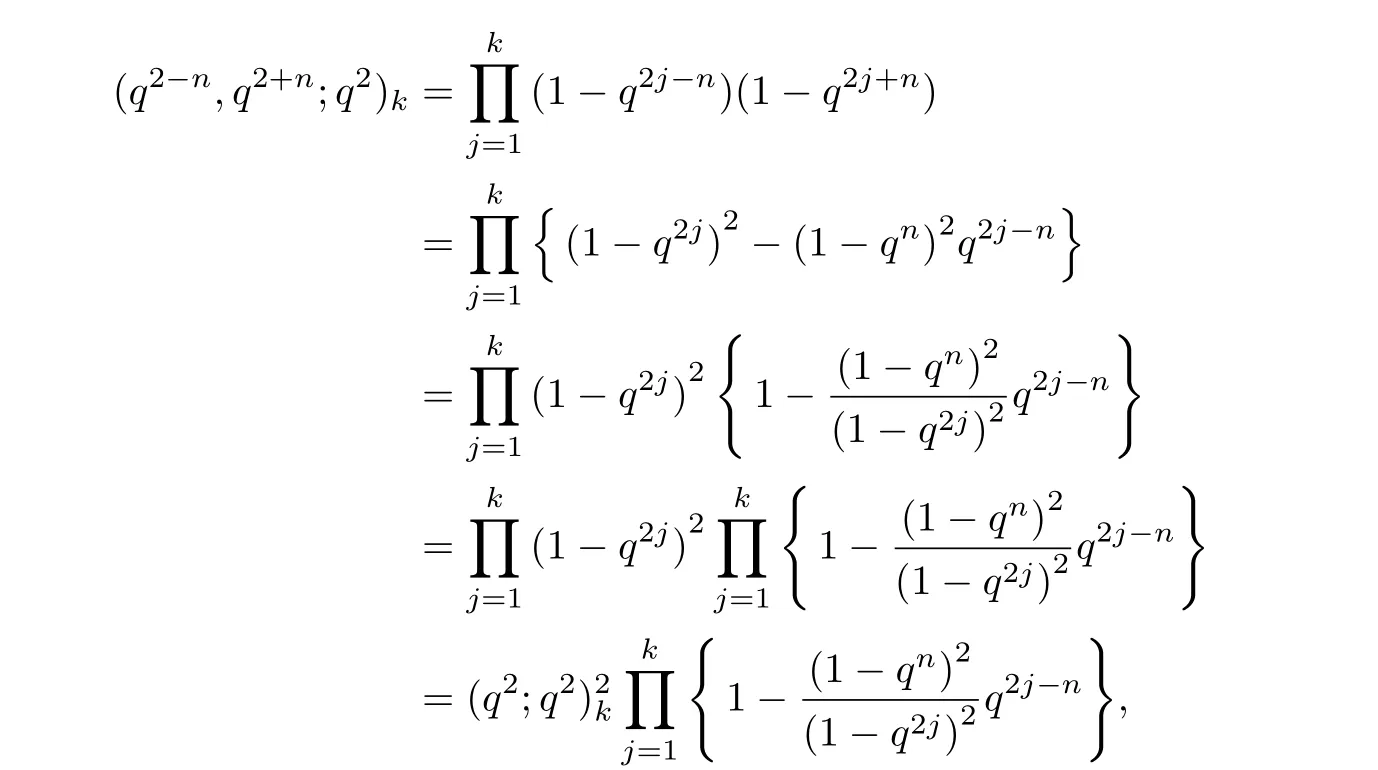
并且注意到

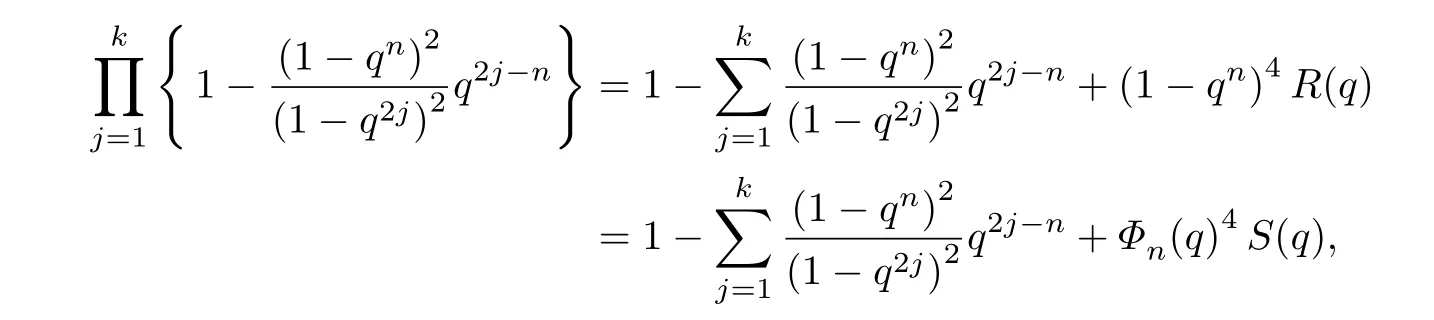
其中R(q) 与S(q) 表示展开式中的剩余部分,能够推导出

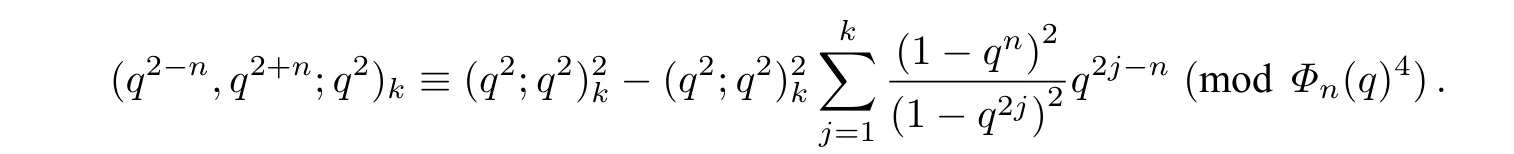
类似地,有

由这两个q-同余式得

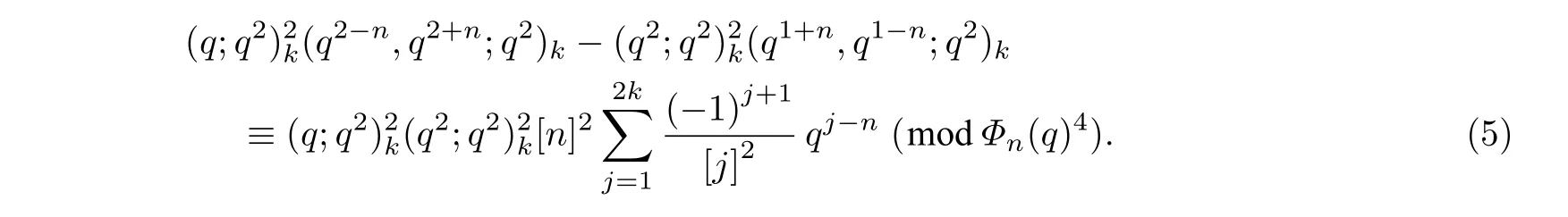
由一个已知的q-同余式[5]改写得

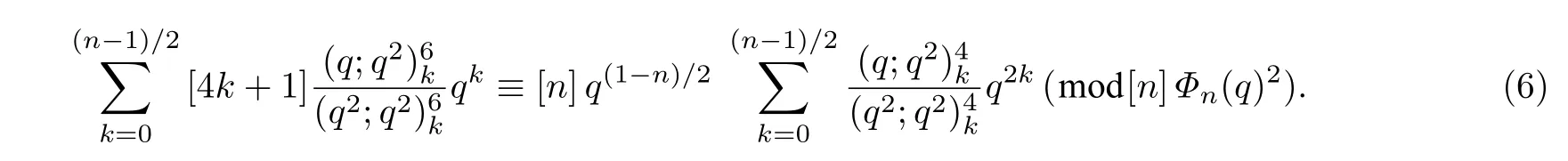
将式(5)和式(6)代入式(4),有

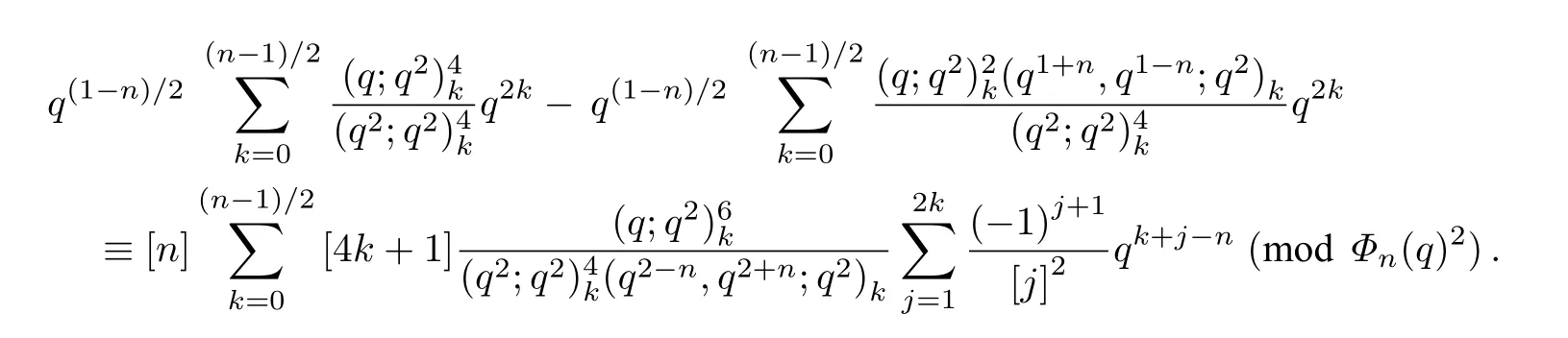
根据关系式

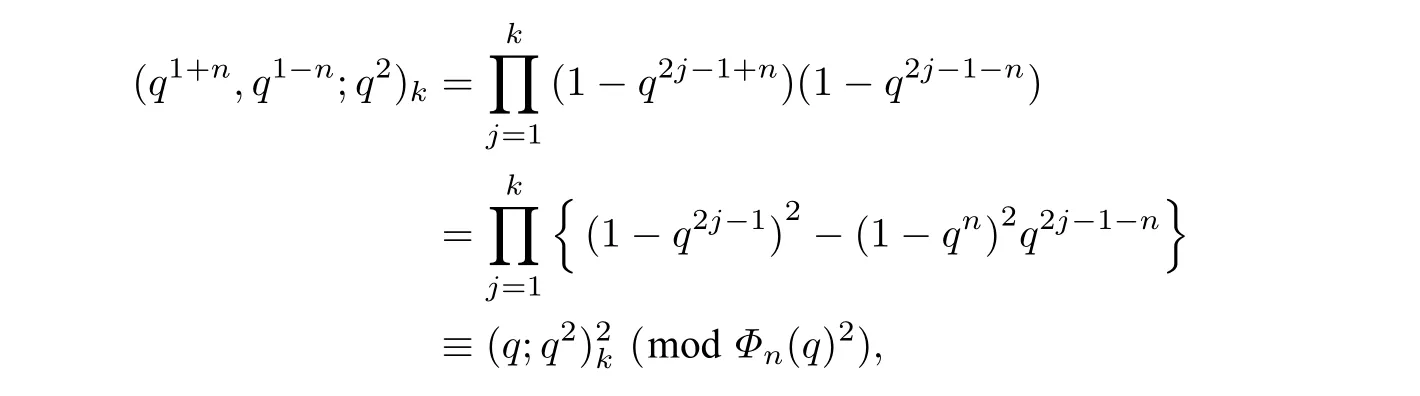
可推导出

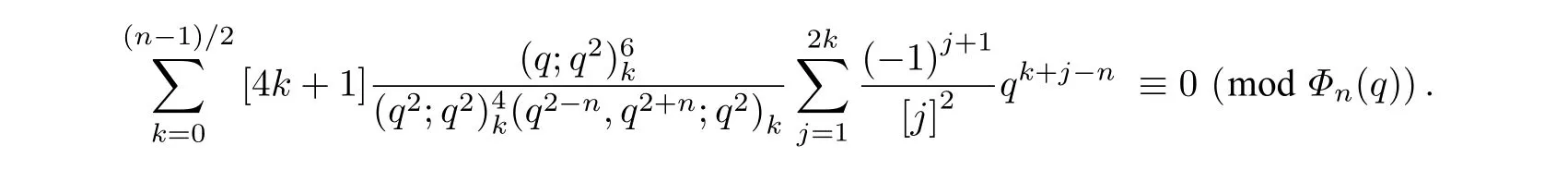
2 定理2 的证明

对式(3)进行参数变换:

与定理1 的证明类似,把式(5)和式(8)代入式(7),得到

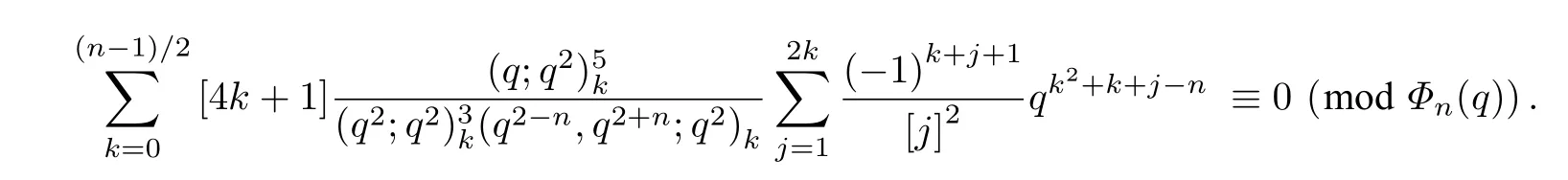
考虑到这个公式与定理2 等价,于是定理2 得证.

3 定理3 的证明

通过式(2),能够建立下列等式:

在式(5)中,用q2替换q,有

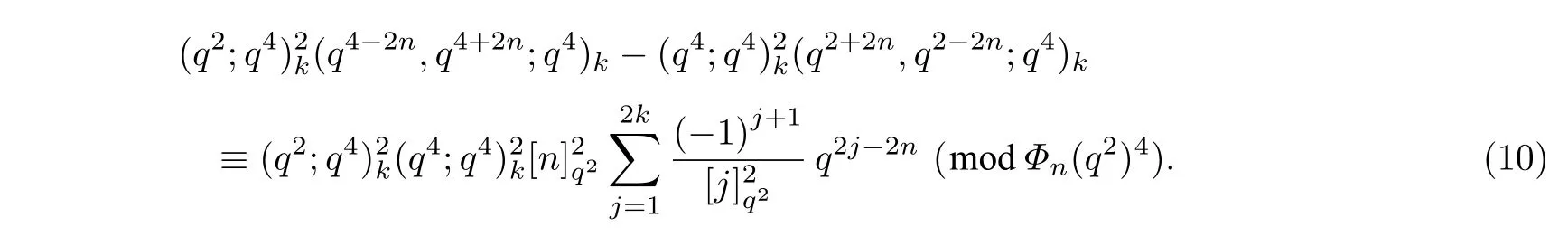
由一个已知的q-同余式[4]得

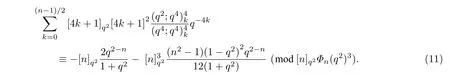
把式(10)和式(11)代入式(9),可以推导出

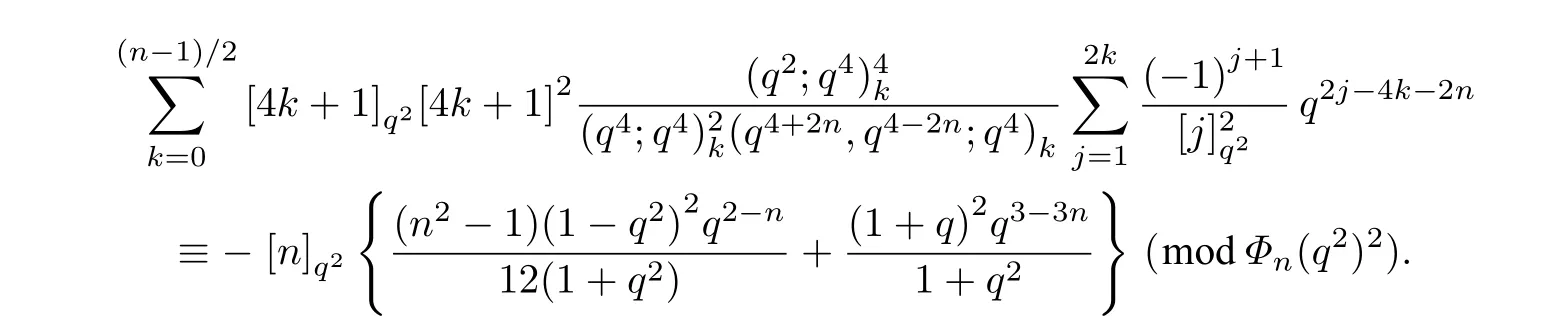
定理3 得证.