基于全局滑模控制的线控转向控制器设计

2022-11-25王艺淇辛世界曲宝军魏家晓曲浩

山东理工大学学报（自然科学版） 2022年1期

王艺淇，辛世界，曲宝军，魏家晓，曲浩

(山东理工大学机械工程学院，山东淄博 255049)

转向系统是汽车底盘的重要组成部分，线控转向(steer-by-wire，SBW)系统采用驱动电机、控制器和多传感器技术提供主动转向等功能并作为新一代转向系统得到了国内外专家的关注[1-2]。

SBW系统中存在许多不确定性因素的干扰，很难对目标进行有效控制，传统的PID控制器难以协调不同工况下的需求[3-5]。汽车行驶中对前轮转角的跟踪速度和跟踪误差要求相对较高[6-7]。为提高系统抗干扰性能和动态响应速度，本文设计了一种新型快速全局滑模控制器(fast global sliding mode control,FGSMC)，并用仿真实验证明了该控制器的有效性和实用性。

1 线控转向系统动力学模型

SBW系统转向执行机构如图1所示，采用电机代替传统转向系统的机械连接装置，通过转向电机产生转矩使齿轮齿条转向器产生齿条位移，最后通过转向臂传递给前轮，保证前轮可以准确跟踪目标转角。

图1 SBW系统转向执行机构

本文采用永磁同步电机(PMSM)作为转向执行电机，不考虑减速器和齿轮齿条的传动误差，SBW系统动力学方程可以表示为

(1)

式中：Je为转向执行电机转动惯量；Be为转向电机阻尼系数；fe为作用在转向执行机构上的等效摩擦力矩；Te为转向执行电机的输出转矩；Jfw为前轮绕主销的转动惯量；Bfw为前轮主销的阻尼系数；δf为前轮转角；Tat为前轮转向回正力矩；kr为转向执行机构传动比。

前轮转向回正力矩Tat主要由主销回正力矩和轮胎拖距回正力矩组成，在正常行驶条件下，假设轮胎拖距为常量，其计算公式为

(2)

式中：Q为车轮载荷；D为主销内移量；γ为主销内倾角；ξ1为气胎拖距；ξ2为后倾拖距；m为汽车质量；v为车速；l为轴距；lr为质心到后轴距离；lf为质心到前轴距离；Cr为后轮侧偏刚度；Cf为前轮侧偏刚度。

为方便研究，将方程(1)改写为

(3)

由方程(3)可以得到SBW系统的状态空间方程

(4)

2 滑模变结构控制器设计

2.1 趋近律设计

SBW系统是一个强耦合、多变量的非线性系统，在设计控制器前，本文对指数趋近律进行改进，引入幂次项和正切函数，实现了更快的收敛速度和控制精度。

指数趋近律为

(5)

式中：k1、k2为常数。

式(5)中趋近律可以在初始状态时快速逼近滑模面，但在逼近过程中速率会逐渐变慢，系统精度降低，造成系统抖振。因此本文对该指数趋近律进行改进，即

(6)

其中sat为切换函数，且

(7)

式中：0<α<1；sn=|s0|+σ，s0为初始状态，σ为正数；ε为抖振指数，ε>0。

在式(6)中，引入的|s|s/(|s|+α)可以加速靠近原点时趋近律收敛速度，正切函数项在接近初始状态时有更大的导数值，通过对σ参数的调节实现更快速的收敛速度，通过以上组合可以实现全局更大限度的快速收敛。用改进的切换函数sat代替原有的符号函数，通过对抖振指数ε的调节，在保证系统精度的情况下抑制了抖振的发生。

2.2 滑模控制器设计

本文定义系统滑模面函数为

s=ce1+e2，

(8)

根据式(8)设计的滑模面和式(6)设计的指数趋近律，设计了FGSMC，即

(9)

式中Dc为待设计与干扰相关的参数。

根据式(5)—式(9)可以将方程(4)描述的SBW系统中的电机控制转矩Te设计为

k2s+k3tan(s/sn)}。

(10)

由式(10)可以看出，当系统状态变量远离滑模面时，通过指数项实现快速收敛，通过正切函数项实现全局更大限度的快速收敛，在接近原点时变指数项提供收敛加速。该控制器有效地解决了收敛速度和抖振问题，并能保证整个系统状态快速精准地收敛到平衡状态。

利用李雅普诺夫理论对系统稳定性进行分析。选取

(11)

滑模面导数为

k1|s|s/(|s|+α)sat(s/ε)-

k2s-k3tan(s/sn)-Dc}。

(12)

因此当s≠0，|s/ε|>1时，

k2s-k3tan(s/sn)-Dc)}=

{cse2-k1s|s|s/(|s|+α)sgns-

k2s2-k3stan(s/sn)-Dc)}≤

-k1(|s|s/(|s|+α)ssgns)≤0；

(13)

当s/ε≤1时，则

k2s2-k3tan(s/sn)s-Dc}≤

-k1s(|s|s/(|s|+α)s/ε)≤0。

(14)

3 仿真与试验

3.1 模型参数选择

在Matlab/Simulink环境下搭建SBW系统仿真模型，模型参数见表1。

表1 模型参数

设定本文所提出快速全局滑模控制器(FGSMC)参数为：c=5，k1=10，k2=10，k3=20，α=0.5，ε=0.05，σ=1，Dc=15，初始转角δf=0 rad。

为验证FGSMC的有效性，将传统滑模控制器(SMC)作为对比控制器进行仿真分析。

3.2 仿真结果与分析

3.2.1 角阶跃信号输入仿真

设车辆纵向速度vx=15 m/s，直线行驶1 s后设置前轮转角的角阶跃输入为0.5 rad，取扰动为0 rad，仿真结果如图2和图3所示。

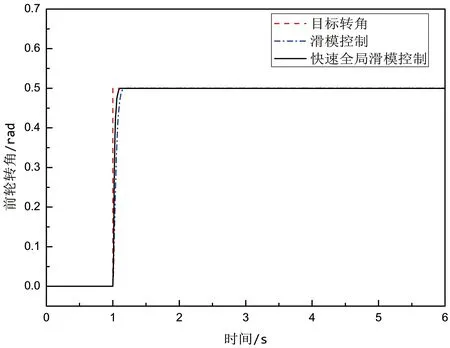
图2 角阶跃信号前轮转角跟踪效果

图3 角阶跃信号前轮转角跟踪误差

由图2可以看出，FGSMC和GSMC可以快速有效地跟踪设定的转角，但FGSMC速度更快，在1.2 s时就达到了稳定状态。由图3可以更加直观地看出FGSMC和GSMC二者误差都在可承受范围内，但在阶跃输入的瞬间FGSMC的误差更小，有更强的鲁棒性。

3.2.2 正弦参考信号输入仿真

设置车辆纵向速度vx=15 m/s，前轮目标转角δfr=sintrad，设置系统干扰随时间取以下不确定扰动：D=0,t∈(0,15]；D=15sin(0.5t),t∈(15,30]；D=30sin(t),t∈(30,50]。图4和图5为SBW系统前轮转角跟踪效果和跟踪误差。

图4 正弦信号前轮转角跟踪效果

图5 正弦信号前轮转角跟踪误差

由图4可以看出，本文提出的FGSMC可以快速准确地跟踪转角设定值，而SMC跟踪出现一定程度的滞后，跟踪速度较慢。由图5可以看出，在扰动发生变化的15 s和30 s时，SMC的误差出现明显波动，FGSMC的波动很小，变化不明显。这表明，本文设计的控制器稳定性和跟踪性能都优于传统的SMC，可以使汽车行驶更加稳定，从而提高了安全性能。