基于模态局部化的耦合悬臂梁能量收集分析
2022-11-25胡帅钊邵明玉刘汉彪张洪瑜马驰骋李波
胡帅钊,邵明玉,刘汉彪,张洪瑜,马驰骋,李波
(山东理工大学 交通与车辆工程学院, 山东 淄博 255049)
生活中的振动能无处不在,如何通过特殊的能量收集器将振动能收集起来转化为其他能量为人类所利用是当前的一个研究热点。压电能量收集方式具有绿色环保、投入成本低、适应环境能力强等优点。随着国内外对能量收集技术的研究,压电收集技术被社会所重视并深入研究,现在已经成为能量收集领域的热门对象之一。振动能收集的方式可分为三种:电磁式、压电式和静电式。
国外关于压电能量收集技术的研究开展较早,已经取得丰富的研究成果。Ajitsaria等[1]建立了双晶型压电悬臂梁的动力学模型,分析了结构的能量收集效率,表明该结构可以提供传感器和数据传输的充足电力。Shi等[2]基于多项式形式的应力函数和归纳函数,分析了不同载荷作用对功能梯度压电悬臂梁能量收集的影响。Izadgoshasb等[3]进行了压电悬臂梁的实际应用,采用理论集中模型把实验测量的加速度作为输入数据预测电压输出。Johnson等[4]设计出微变形的压电悬臂梁,将小振幅机械振动转换为可用于低功耗电子设备的能源。Zhao等[5]基于有限元方法设计压电悬臂梁,进行了低频振动实验设计和性能分析,结果表明低频条件对能量收集效率有所提高。Lin等[6]提出了一种耦合压电效应的瞬时最优闭环控制算法,进行了自适应控制分析,分析了两者之间的耦合作用。Bonello等[7]基于能量捕获光束的替代建模原理,提出了一种双晶型能量收集结构。
国内关于压电能量收集技术的研究开展稍晚,但是近年来取得了丰硕的研究成果和应用产品。李彬[8]进行了低频宽频带压电振动能量收集研究,设计出能在低频、宽频带条件下高效收集振动能量的六阶折叠悬臂梁压电收集器。刘红俊[9]基于压电效应原理建立相应的数学模型和有限元分析模型,旨在优化和改善低频换能器结构,增加工作振动频率带宽,提高输出响应性能。于斌[10]研究低频驱动悬臂梁振动能量收集器,设计出低频驱动悬臂梁能量收集器实物,并对采集器进行了物理测试。费立凯[11]基于电站低频环境影响,设计和分析压电振动悬臂梁结构,通过结构理论分析确定出合适的模型。杨炯炯[12]将非线性弹簧与传统的双稳态压电式俘能系统相结合,提出了含非线性弹簧的双稳态压电式振动俘能装置,从而达到更好的动力学输出响应。查宏[13]进行了压气机离心叶轮错频叶盘结构的模态和振动响应分析,比较了不同模态局部化下叶轮的模态振型和强迫振动响应幅值。洪婧[14]基于模态局部化的四耦合悬臂梁质量感知方法,确定了最优耦合因子。李晓东[15]基于模态局部化的耦合悬臂梁质敏机理,建立了耦合悬臂梁结构的弹簧-质量-阻尼模型,分析了系统的模态局部化振动特性,提出了外界扰动对系统谐振特性的作用机制。学者侧重对低频带环境以及能量收集器的外形研究,很少考虑模态局部化对系统的影响,模态局部化能够改变系统的固有频率,降低制作成本。针对研究结构的不足,为了提高能量采集的实用性,本文提出基于模态局部化的耦合压电悬臂梁的设计,以降低压电振动能量收集器的固有频率,提高能量收集效率。
1 数学方程
基于模态局部化的原理,本文采用图1所示的结构进行能量收集研究,该结构由两个悬臂梁通过中间部分弹性连接,两个悬臂梁的长度分别为a+d、a+d-δ,厚度为h,弹性模量为E,密度为ρ,中间的连接长度为c。
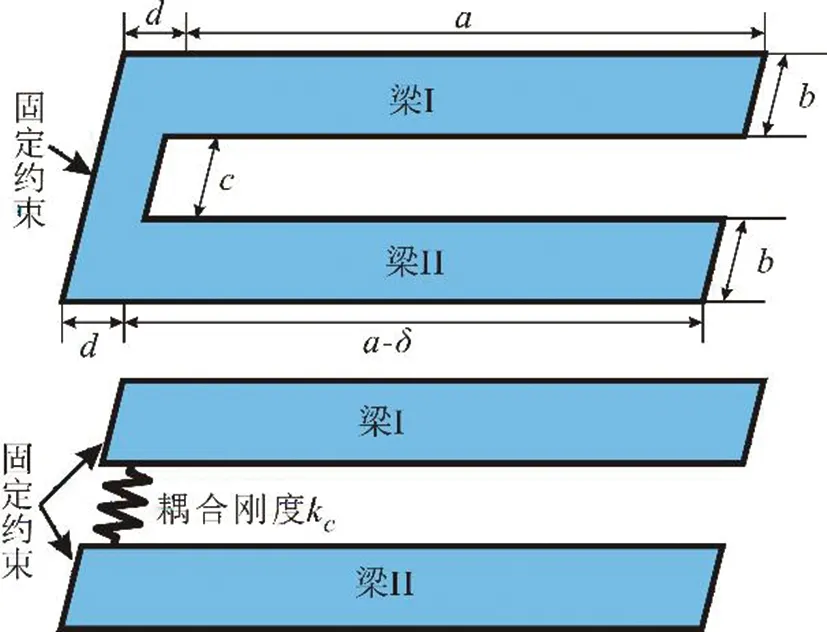
图1 机械式耦合悬臂梁简化力学模型
对于图1所示的系统,根据简化力学模型,其弹性变形能V和动能T可以通过Euler-Bernoulli梁理论得到:
(1)
(2)
式中:Kc为耦合刚度;w1为左悬臂梁的挠度;w2为右悬臂梁的挠度;Ib为横截面对中性轴的惯性矩;A为横截面的面积。
(3)
为求解微分方程(3),需要施加必要的边界条件,由于梁结构为悬臂梁,因此对于梁I和梁II,边界条件为:
(4)
(5)
根据模态叠加法(mode superposition method,简称MSM),式(1)的解可以表示为模态组合的形式,即
(6)
式中:n表示模态阶数;qi(t)为广义坐标;φi(x,t)为瞬时模态。
机械式耦合悬臂梁的左、右梁均采用等截面的类型。其边界条件满足一端固定,另一端自由振动,因此可以用等截面横向振动频率方程进行求解。等截面横向振动频率计算式为:
cos(βl)ch(βl)=-1,
(7)
Yi(x)=Ci[cos(βix)-ch(βix)+
ri(sin(βix)-sh(βix))],
(8)
ri=(sin(βil)-sh(βil))/(cos(βil)+
ch(βil)),
(9)
式中:Ci代表常数;βl为等截面梁频率方程的根;l为悬臂梁的梁长。
通过定积分求出与固有频率相关的系数,定积分为:
(10)
(11)
(12)
(13)
通过Galerkin方法可以得到变质量梁系统的振动控制方程:
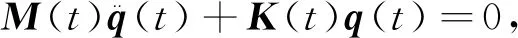
(14)

(15)
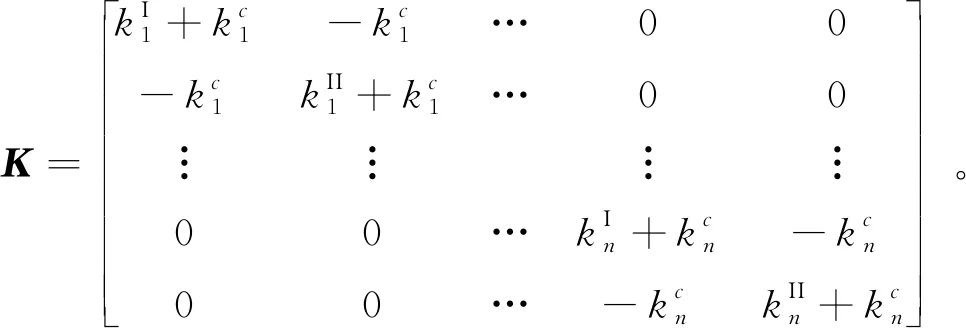
(16)
当仅考虑梁I和梁II的第一阶振型时,系统的质量矩阵和刚度矩阵为:
(17)
采用Rayleigh比例阻尼形式,C=αM+βΚ, 则阻尼矩阵为
(18)
首先计算结构的无阻尼频率,简化后的模型如图2所示,其中M1代表左悬臂梁,M2代表右悬臂梁;K1代表左悬臂梁的刚度系数,K2代表右悬臂梁的刚度系数,二者之间的连接可以看成刚度系数为Kc的弹簧连接;左右两端进行固定。
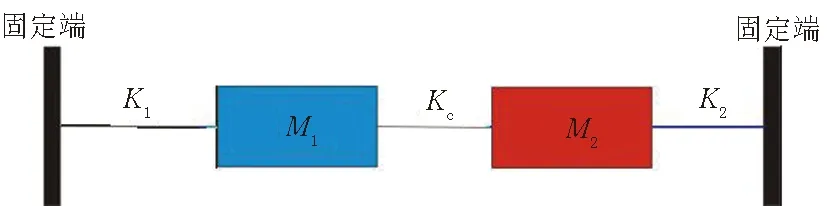
图2 简化后的悬臂梁模型
将式(10)—式(13)的计算结果代入式(14),可以得出质量矩阵M和刚度矩阵K,然后通过MATLAB软件进行编程求(M,K)的特征值,进而求得只含Kc的结果。
取铝合金悬臂梁,其梁长为0.2 m,横截面积A=0.002×0.025 m2为例,通过理论公式的推导计算,求出该悬臂梁的第一、二阶固有频率分别为41.1、257.7 Hz。通过软件仿真结果分别为41.2、259.9 Hz。理论公式推导的计算结果与ANSYS仿真结果非常接近,这说明了推导公式的正确性,为后续实验验证提供了理论依据。
2 模型设计
通过文献阅读,在压电式振动能量收集器的研究成果中,降低谐振频率或者提升带宽是提高压电能量收集器能量收集效率的关键因素。本文设计不同尺寸的矩形压电悬臂梁,仿真与实验分析输出响应的影响因素。
2.1 能量收集器的整体结构
能量收集器的整体设计分为4个步骤,分别为建模分析、仿真实验、实物制作和实验验证。本文设计的压电悬臂梁能量收集器主要由3部分组成:铝合金悬臂梁,靠黏液粘贴的压电片和2根电路导线。压电片比较薄,在设计的同时,还要保证压电片不被破坏,因此选择硬度相对较弱的悬臂梁。压电片的厚度为0.5 mm,长和宽分别为4 cm和2 cm。结构示意如图3所示。红色部分表示悬臂梁,蓝色部分表示压电片,铝合金悬臂梁由2个悬臂梁左右耦合而成,左端黑色部分表示约束,也就是说整体能量收集器被固定。采用激振器不断地给系统提供的激振力,使得系统发生振动,从而达到收集能量获得电能的目的。为了获得较大的能量输出效应应将压电片粘贴在悬臂梁的根部。

图3 压电悬臂梁的结构图
2.2 压电悬臂梁的仿真分析
利用ANSYSAPDL软件对压电悬臂梁进行仿真分析,其有限元分析的具体过程分为4个阶段,分别为制作压电悬臂梁、建立几何模型、有限元模型模态分析、获得结果。通过设置尺寸和坐标对压电悬臂梁进行有限元建模,为了缩短建模时间和改变尺寸时方便建模,后续采用命令流的方式进行建模。建立的实体模型如图4所示。

图4 悬臂梁的实体建模
本文共设计9组悬臂梁模型,先对其中1个模型进行仿真。压电悬臂梁的俯视图如图5所示。
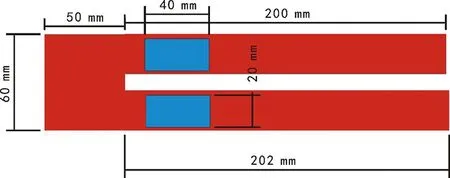
图5 悬臂梁模型的俯视图
耦合刚度Kc不能直接获取。通过模态叠加法计算出单悬臂梁的刚度矩阵和质量矩阵,耦合悬臂梁由左、右悬臂梁以及弹簧耦合组成,通过振动微分方程列出含耦合刚度Kc的运动方程,将ANSYSAPDL仿真结果与理论结果进行对比进而求出Kc,得到Kc随d的变化曲线如图6所示。左、右悬臂梁可以看成由一个弹簧连接,这个弹簧的刚度系数为Kc,耦合长度为d,当d从10 mm变化到20 mm时,Kc从40.8变化至10.1,从而可以得出随着d的增加,Kc呈减小趋势。
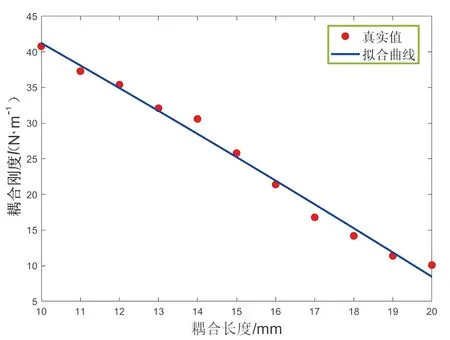
图6 耦合刚度与耦合部分长度的关系曲线
利用ANSYSAPDL软件对建模后的模型进行网格划分。为研究压电悬臂梁能量收集效率的影响因素,本文设计不同尺寸的悬臂梁。为使研究更有说服力和针对性,设计出只改变左右悬臂梁长度的不同规格悬臂梁。模型序号为1—9,表1、表2为不同尺寸d的压电悬臂梁的前两阶固有频率。
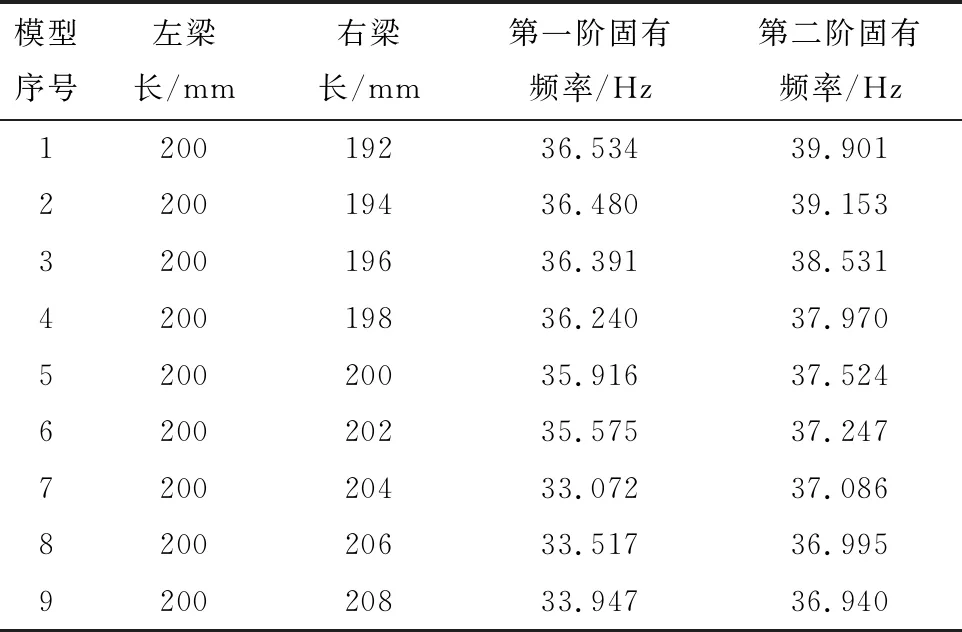
表1 d=10 mm时压电悬臂梁的前两阶固有频率
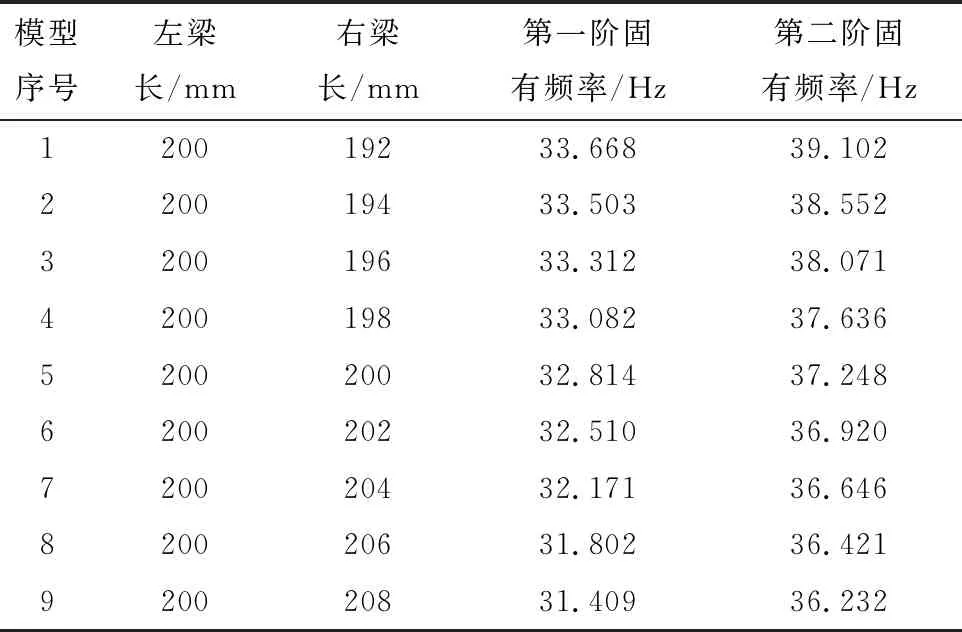
表2 d=20 mm时压电悬臂梁的前两阶固有频率
由表1、表2可知,当d=10、20 mm,悬臂梁按不同的方式固定,系统会出现不同的固有频率。随着右悬臂梁的长度逐渐增加,压电悬臂梁的前二阶固有频率均逐渐减小。此时,压电材料发生正压电效应的能力逐渐变强,能量收集效率也会逐渐提高。系统的固有频率与耦合长度也有联系。随着d的增大,系统的固有频率呈现降低的趋势,不同类型的压电悬臂梁都有效地将前二阶固有共振频率控制在30~40 Hz范围内,这意味压电悬臂梁满足在低频环境中供电的条件,适当改变悬臂梁的梁长,系统的谐振频率也会发生改变。因此根据实际环境中的自然振动频率,有效改变悬臂梁的长度,可以有效地提高能量收集器的收集效率。
3 压电悬臂梁的实验测试
3.1 振动能量收集器的制作
振动能量收集器制作由4个部分组成,分别为制作压电悬臂梁、压电片的粘结、引出电极以及压电片尺寸的选择。
3.2 实验测试和结果分析
主要设备有HVP-1070B功率放大器、DG1032信号发生器、激振台、示波器和电源,实验平台示意如图7所示。整个实验平台的工作原理是:打开电源,信号发生器输出正弦波信号,该信号被传递给功率放大器;功率放大器将收到的信号通过驱动信号传递给激振器,从而激振器为压电悬臂梁提供持续激励;示波器测出能量收集器的输出电压与时间的关系曲线,并以Excel的形式导出数据。

图7 实验平台
仿真、理论计算与实验测试系统固有频率与悬臂梁尺寸的关系曲线如图8所示。由图8可知,悬臂梁长度的差值从-8 mm变化为8 mm且耦合长度为10 mm时,能量收集器系统的第一阶固有频率从38.92 Hz下降到36.90 Hz,系统的第二阶固有频率从43.13 Hz下降为41.21 Hz;耦合长度为20 mm时,系统的第一阶固有频率从34.04 Hz下降到31.04 Hz,系统的第二阶固有频率从41.94 Hz下降到38.89 Hz。从变化结果可以得出改变悬臂梁的梁长范围,可以有效降低系统的振动频率,从而有效提高能量收集效率。仿真与实验结果在误差范围以内,这证明了实验的准确性。

(a)耦合长度10 mm
通过示波器测出振动能量收集器的电压,绘制在d=20 mm时压电悬臂梁的电压随时间变化关系曲线如图9所示。激振器为系统提高基础激励,随着时间不断变长,系统所提供的外界激振频率不段增加,压电悬臂梁发生的形变不断增加,当外界激振频率与系统的谐振频率相等时,系统发生共振,压电悬臂梁达到最大的形变,从而系统发出最大的电压。因为不同模型的悬臂梁长度差值不同,导致了系统的固有频率也不尽相同,系统达到共振要求也不同,适当改变系统的谐振频率,系统更容易达到共振,从而压电悬臂梁发生最大形变,为系统提高最大的电压,进而提高系统的能量收集效率。将示波器测定的电压与时间关系经过傅里叶变换得到图10。悬臂梁左右梁长度差值的变化,影响系统的固有频率,当给系统提供基础激励时,因其固有频率不同,压电悬臂梁发生的形变也存在差异,形变的大小影响系统的电压输出。如果在一定的基础激励下,系统所需要的固有频率越低,那么系统越容易达到要求,越能尽快地达到最大形变,进而提供最大的电压输出,从而提高能量收集效率。由图10可知,振动能量收集器的固有频率与悬臂梁的长度差值呈负相关关系,固有频率低的悬臂梁,对外界激振频率要求低,更有利于能量收集。系统中首先是主悬臂梁发生共振,然后耦合悬臂梁发生共振。因此能量收集效率和输出电压不仅受悬臂梁尺寸的影响,还和压电悬臂梁所固定的位置有关。
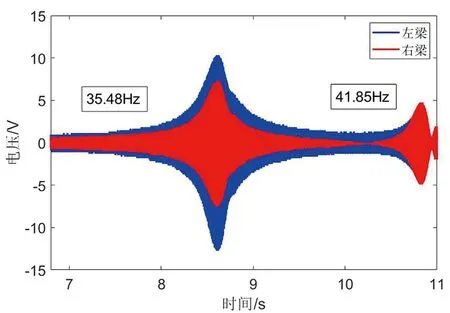
(a)右、左梁长度差值-8 mm,耦合长度20 mm
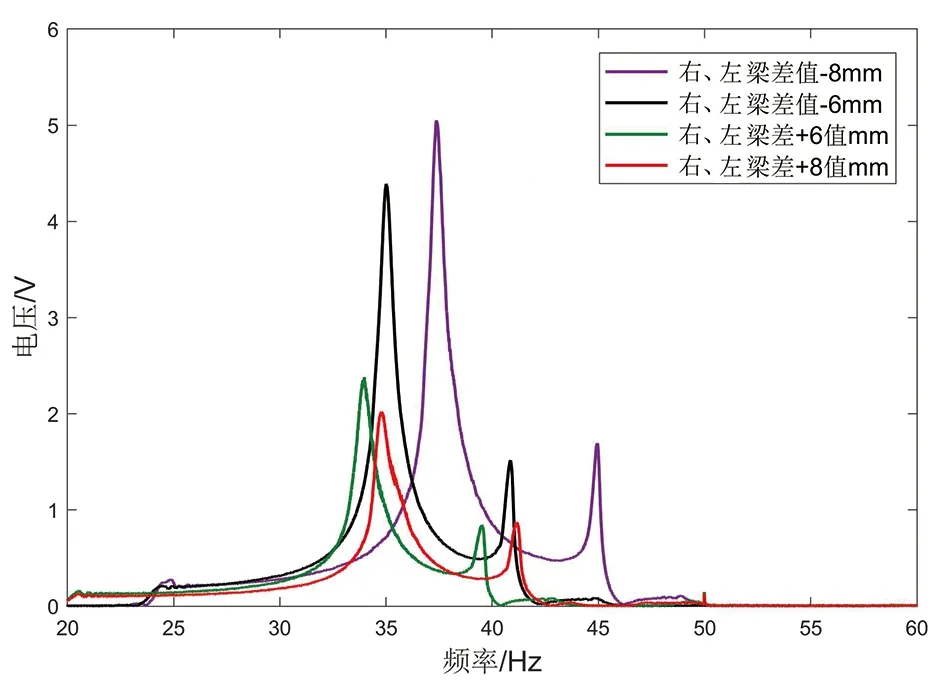
图10 傅里叶变换图
图11为图9所示5组模型的电压与功率对比图。当系统发生共振时,耦合悬臂梁发生最大的形变,系统得到最大的电压和功率。从图11可知,改变悬臂梁的左右悬臂梁长度,从而减小系统的固有频率,增大压电悬臂梁的最大形变,系统的电压和功率得到了有效提高。

图11 5组模型电压与功率对比图
4 结论
本文设计不同尺寸的压电悬臂梁,通过ANSYSAPDL软件对振动能收集器进行仿真,根据仿真结果制作9组压电悬臂梁能量收集器实物样机,并针对其输出电压、固有频率及能量收集效率进行了实验与仿真。实验结果与仿真结果相互佐证。分析了影响压电悬臂梁能量收集器能量收集效率的因素,得出以下结论。
1)压电悬臂梁振动能量收集器的固有频率与悬臂梁的尺寸呈负相关关系,实验结果与仿真结果显示,当改变悬臂梁的尺寸时,系统的固有频率会发生改变,为了让能量收集器适应工作环境,因此根据周围振动环境的振动频率,制作出符合环境要求的能量收集器,提高振动能量收集器的能量收集效率。
2)本文所设计的9种压电悬臂梁在保证输出功率的前提下能够在低频环境下收集振动能量。从实验结果来看振动能量收集器的特征频率大约在33~40 Hz之间,这表明了该振动能量收集器能够在较宽的频带中进行工作,基于模态局部化的耦合悬臂梁可以提高系统的共振频率频宽,提高收集能量的效率。
