马铃薯片热泵干燥动力学研究及其干燥工艺优化

刘海波 , 王佳倩, 李 耀, 金雪冻, 朱 静, 王 辉, 刘 雄

(信阳农林学院1，信阳 464000) (西南大学食品科学学院2，重庆 400715) (贵州省生物技术研究所3，贵阳 550006)

马铃薯(SolanumtuberosumL.)，又名土豆、洋芋、山药蛋等，作为三大主粮的补充，富含碳水化合物、蛋白质、无机盐和维生素等营养物质，具有“营养之王”的美称[1-3]。除了鲜食和饲用外，大量的马铃薯要进行长期储存保藏，但新鲜的马铃薯含水量在80%以上，由于其含水率高、上市量集中且运输成本高，不便于长期储藏，若不及时处理较易腐烂变质，造成严重的资源浪费[4，5]。因此，干制马铃薯片成为新鲜马铃薯的主要加工产品，对满足市场需求具有重要意义。

干燥是制作马铃薯片中必不可少的工序，其主要目的是除去水分，防止细菌、霉菌等微生物的滋生造成营养物质的流失[6]。在食品工业中，常用的干燥方式有喷雾干燥、真空冷冻干燥、微波干燥、对流干燥、热泵干燥等[7-11]。热泵干燥是以热空气为干燥介质，将热量传递给物料，使其表面的水分汽化，内部和表面之间产生水分梯度差，内部的水分因此以气态或液态的形式向表面扩散，从而达到干燥的目的，具有高效节能、操作简单、适用范围广、经济环保且能保证产品质量的优点，因此被用于粮食、水果等产品的干燥[12]。Taseri等[13]进行了葡萄渣的热泵干燥动力学研究及品质参数的测定，发现空气流速度对干燥时间略有影响，但在相同温度下空气流速对功耗没有显著影响；Wang等[14]以山楂饼为干燥原料，利用热泵干燥机进行结构优化，设计出具有更高效率的热泵干燥系统；Xiong等[15]研究发现热泵干燥的荔枝果渣粉末中的结合酚含量高于热风干燥的荔枝果渣粉末；Aguirre-alonso等[16]开发了热泵和N2喷雾干燥香草乙醇提取物的状态空间热力学模型，模型表明热泵喷雾干燥的热效率可达58%，而传统喷雾干燥只有30%。

限于现代干燥技术，要实现物料在干燥过程中水分的实时监测仍是个难题，因此，了解干燥过程中水分的变化规律，对工业生产和提高产能具有重要意义。在食品干燥过程的研究中，动力学模型正是可以描述物料水分比随干燥时间变化的函数，然而目前鲜见国内外学者对马铃薯片热泵干燥的动力学模型部分的研究。因此，本实验将对马铃薯片热泵干燥过程中的动力学模型进行研究，并探索适宜的干燥工艺，为热泵干燥在马铃薯等农产品中的应用提供参考。

1 材料与方法

1.1 实验材料

实验中所用的马铃薯为同一批次的新鲜马铃薯，品种为合作88，初始含水量为(82.65±0.32)%；块茎成熟度及大小均匀，芽眼较少，表皮无霉变、无发绿及机械损伤。

1.2 仪器与设备

HH-6D型数显恒温水浴磁力搅拌器，WB-KQ01型热泵(移动除湿烘干机)，DHG-9070型电热恒温鼓风干燥箱，UltraScan PRO型测色仪。

1.3 样品制备

原料挑选→清洗→去皮→切片→漂洗→沸水烫漂(3 min)→凉水冷却→沥水、擦干表面水分→热泵干燥→马铃薯干片。

1.4 方法

1.4.1 水分含量的测定

采用常压干燥法，按照GB 5009.3—2016 《食品安全国家标准 食品中水分的测定》[17]测定。以样品的干基含水率为准，取各时刻的样品进行水分含量测定，平行3次实验，取平均值。按式(1)计算样品的含水率。

(1)

式中：Mt为物料干燥至t时刻的干基含水率/g水/g干物质；mt为物料干燥至t时刻的质量/g；mg为绝干物料质量/g。

1.4.2 试样干燥速率

(2)

式中：Dr为物料干燥速率/g/(g·h)；Mt+Δt为物料(t+Δt)时刻的干基含水率/g/g(g水/g干物质)；Δt为干燥间隔时间/h。

1.4.3 物料水分比

(3)

式中：MR为物料水分比，无量纲；Me为物料干燥到平衡时的干基含水量/g/g；Mt为物料干燥到t时刻的干基含水率/g/g；M0为物料初始干基含水率/g/g。由于平衡干基含水量Me远小于Mt，可以忽略不计，所以式(3)可以近似简化为式(4)。

(4)

1.4.4 有效水分扩散系数计算

扩散系数的大小反映了特定条件下样品失水能力的大小[18]，是反映干燥设备好坏的重要指标之一。将薄片状物料近似无限平板，通过Fick第二定律表示为：

(5)

实验干燥时间较长，即n=1，并对MR取对数，则公式化简为：

(6)

式中：Deff为有效水分扩散系数/m2·s-1;L为马铃薯片厚度/m。

由式(6)可知，有效水分扩散系数由-lnMR与干燥时间t的趋势线斜率的关系为：

(7)

(8)

1.4.5 色泽的测定

将样品粉碎，过30目筛，装入自封袋后使用测色仪对样品进行色差测定，依次读取L*值、a*值、b*值，并计算ΔE*值，平行8次测量，取平均值。L*值表示亮度；a*表示红绿值，“+”表示偏红，“-”表示偏绿；b*表示黄蓝值，“+”表示偏黄，“-”表示偏蓝；ΔE*表示干制品的色泽与新鲜样品色泽差异大小，ΔE*值越小越好，其计算公式为：

ΔE*=

(9)

式中:L0、a0、b0分别表示新鲜样品的亮度、红绿值、黄蓝值。

1.4.6 复水比的测定

将干燥不同时长的各组样品分别取2 g左右放入水浴锅中，90 ℃恒温浸泡30 min后取出放在无风处沥水20 min，再用滤纸吸去表面水分，最后称质量，计算复水比[19]。按式(10)计算样品的复水比。

(10)

式中：m1为样品复水后沥干水分所称得的质量/g；m0为样品复水前的质量/g。

1.4.7 干燥动力学模型研究

目前干燥研究大多认为扩散是水分迁移的主要途径[20],物料内部水分扩散是一个复杂的传质过程，涉及分子扩散、毛细流动、水力学流动和表面扩散等现象[21]。要利用动力学模型描述物料在干燥过程中水分随时间的变化规律。

1.4.7.1 干燥动力学模型的选择

物料干燥的过程中涉及到很多复杂的传热传质过程，因此建立物料干燥动力学模型对研究干燥规律及工艺参数具有重大意义。同时，模型选择的合适与否也将直接影响实验值与预测值的误差大小。依据文献报道的果蔬干燥动力学模型，对马铃薯片热泵干燥过程，进行数据拟合验证，用决定系数(R2)评价模型的适用性，R2越接近1，说明模型的匹配度越高。计算公式为：

(11)

式中：MRexp,i和MRpre,i分别为第i个数据点的实验测定MR与模型预测MR；N为实验数据点的数量。

1.4.7.2 马铃薯切片干燥实验

选用同批次、大小相近的土豆进行热泵干燥实验，将马铃薯洗净去皮后切片，厚度为3～5 mm，在物料托盘上均匀平铺一层，确保物料仅在上下表面进行传质。在干燥过程中，由于物料厚度远小于其直径，所以物料可被假定为大平板。忽略温度梯度导致的水分扩散，物料中的水分扩散可被假设为沿物料内部厚度方向的一维扩散过程。干燥过程中，每隔30 min(根据实验实际操作情况及条件而定的间隔时长)将物料迅速取出并称质量，记录不同时刻马铃薯片的质量后将物料放回继续干燥，直至物料含水率不大于13%(湿基)，此时水分比达到0.03，即认为已达到平衡含水率，停止干燥[20]。

以切片厚度、干燥温度、样品装载量为单因素，控制其他因素不变进行干燥实验，根据样品在各条件下的干燥曲线和感官品质综合情况分别对各因素范围进行初筛选，为正交设计因素水平的选取做准备，实验方案见表1。

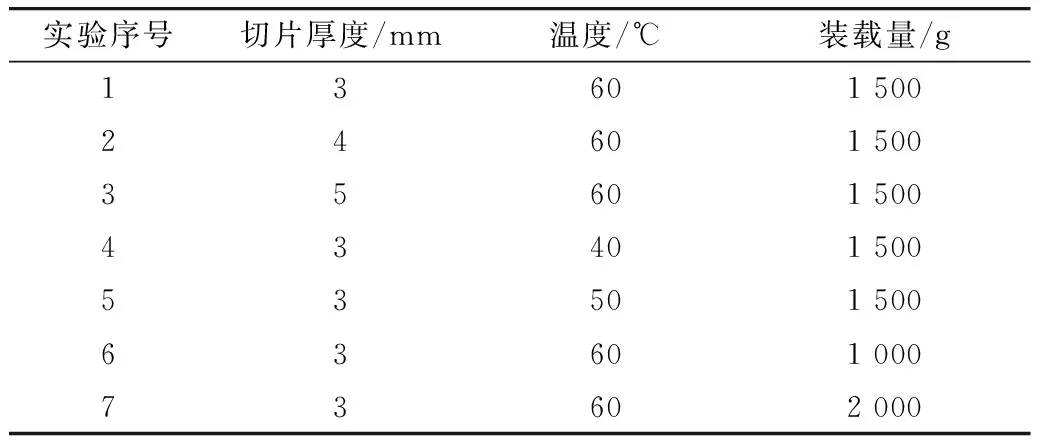
表1 马铃薯切片干燥方案

1.5 正交设计实验

在干燥实验的基础上，选取切片厚度、干燥温度、样品装载量3个因素，以马铃薯干片的色差(ΔE*)和复水比为考察指标，进行三因素三水平的L9(34)正交实验。正交实验因素水平见表2。

表2 正交实验因素水平表

1.6 数据统计与分析

所有的实验结果均用平均值±标准偏差(n=3)表示，使用Excel 2010与SPSS 22.0版统计软件对实验数据进行处理和显著性分析(显著性水平P<0.05)，用Origin 8.6软件制图、回归分析并进行模型拟合。

2 结果与分析

2.1 不同切片厚度对干燥过程的影响

在热泵干燥温度60 ℃，装载量1 500 g时，马铃薯切片的厚度(3、4、5 mm)对干燥过程的影响，见图1和图2。由图1可知，随着切片厚度的减小，马铃薯水分下降速率加快，经相同时间干燥物料的水分比值也越小，这是因为马铃薯片越薄，单位体积的表面积增大，与热空气的对流换热面积增大，传热传质速率增加[20]。干燥至水分比为0.03(含水率为13%)时，3 mm厚度的切片用时3.5 h，相较于4、5 mm分别缩短了41.67%(6 h)、46.15%(6.5 h)，很大程度提高了干燥速率。由图2可知，随着干燥的进行，不同厚度的切片干燥速率整体均呈现先升高后下降的趋势，且切片厚度越小，干燥速率越大。不难发现，厚度为3 mm的切片干燥速率远大于干燥速率较为接近的4、5 mm的切片。因为切片厚度越小，致使传质阻力越小，干燥速率就越快，越早达到平衡含水率，有利于干燥的进行，节省能源。但预实验发现当切片厚度小于3 mm时，蜷曲较大且易碎裂，影响外观品质和包装、运输性能，故切片厚度选择3 mm适宜。

图1 不同切片厚度下的MR-t关系曲线

图2 不同切片厚度下的干燥速率曲线

2.2 不同温度对干燥过程的影响

在马铃薯切片厚度为3mm，装载量1 500 g时，热泵干燥温度(40、50、60 ℃)对干燥过程的影响见图3和图4。由图3可知，马铃薯切片的水分比随着干燥时间的延长而下降，且温度越高，干燥曲线越陡，样品达到相同含水率的时间越短，水分比值越小。这是因为温度升高不仅使得传热速率增加进而加速了样品表面水分的蒸发速度，而且降低了热泵干燥室内空气的相对湿度，使得样品表层水分向干燥气体的扩散动力增加，进而缩短物料的干燥时间。由曲线的斜率可以看出，前中期干燥速率快，后期逐渐减少，这是由于随着干燥的进行，物料的水分不断减少，水分梯度的作用越来越小，干燥界面内移，干燥过程由表面传质控制转化为内部扩散控制，干燥曲线的斜率越来越平坦[20]。另外，由图3可知50 ℃和60 ℃的干燥曲线很接近，干燥至目标含水率13%用时均约3.5 h，而40 ℃干燥则需要6.5 h，耗时长，效率低。由图4可知，温度越高，马铃薯切片的干燥速率越大。随着干基含水量的降低，干燥速率呈现出短时间的上升和长时间的下降趋势，即可将干燥过程主要分为加速和降速两个阶段，且降速阶段远长于加速阶段。这是因为随着物料内部含水量的逐渐减少，水分从内部迁移到表面的速率和从表面蒸发到周围空气中的速率都随之降低，从而导致干燥速率逐渐减小[22]。其中，40 ℃和50 ℃条件下有一小段恒速阶段，而60 ℃并未出现此情况，反而出现一段先降速后加速的阶段，这可能是由于干燥温度过高使得切片表面水分迅速扩散殆尽，而切片内部水分还未来得及扩散转移至切片表面蒸发所致。在物料含水量(干基)相同的情况下，温度越高，物料干燥速率越大，干燥时间就越短，但在整个干燥过程中，50 ℃和60 ℃的干燥速率差别不明显。故综合考虑，50 ℃干燥较为适宜。

图3 不同干燥温度下的MR-t关系曲线

图4 不同温度下的干燥速率曲线

2.3 不同装载量对干燥过程的影响

在马铃薯切片厚度为3 mm，温度为60 ℃时，不同装载量(1 000、1 500、2 000 g)对干燥过程的影响见图5和图6。由图5可知，在切片厚度、干燥温度相同的情况下，装载量越小，马铃薯切片干燥耗时越短，含水率降低越快。将物料干燥至含水量(湿基)≤13%时，装载量分别为1 000、1 500、2 000 g对应的干燥时间分别为3.0、3.5、5.0 h。装载量越大导致干燥时间延长，这可能是因为随着装载量增加，干燥过程中所要除去的水分也相应增加， 而单位时间内蒸发排出水分的能力是一定的，从而导致时间延长。由图6可知，在整个干燥过程中，不同装载量的干燥速率整体均呈现出先短时上升后长时下降的趋势，可看出装载量为1 000 g时平均干燥速率最大，装载量为2 000 g时干燥速率最小。这是因为在热泵干燥初期，干燥介质供给的热量主要用于提高物料温度，用于使物料水分蒸发的热量较少，因此随着装载量的增加，干燥速率变慢[23]。另外，装载量为2 000 g时表现出较为典型的干燥速率曲线，与1 000 g和1 500 g的情况略有不同。可能是因为装载量为2 000 g时样品总含水量比较多，在干燥过程中物料表面水分蒸发用时延长，使得内部水分有更多时间扩散迁移至表面，不会出现物料过少时干燥速率先下降后上升的特别现象。

图5 不同装载量下的MR-t关系曲线

图6 不同装载量下的干燥速率曲线

2.4 干燥动力学模型研究

2.4.1 干燥动力学模型的选择

目前常用的薄层物料干燥模型主要有几种：

1)指数模型Lewis[24]：MR=exp(-kt)，该模型主要考虑了物料表层及边界层对水分扩散运动的阻力[25]。

2)单项扩散模型Henderson and Pabis[26]：MR=Aexp (-kt)，该模型已被用于描述带穗谷物、小麦和玉米等物料的干燥动力学特性。

3)Page方程：MR=exp(-ktn)，该模型是对Lewis修正后得到的，用于描述玉米、向日葵、稻谷、大豆、人参、罗非鱼鱼片等多种物料的薄层干燥特性[27]。

4)Logarithmic[28]模型：MR=Aexp (-kt)+c

5) Wang and Singh[29]：MR=1+at+bt2

6)Midilli[30]：MR=Aexp (-ktn)+bt

7)Verma[31]：MR=Aexp (-ktn)+(1-a)exp (-gt)

将这7种常用的干燥动力学模型方程进行线性化处理，找出其线性关系以便于后续进行模型的筛选、分析和比较，各模型方程线性化处理结果见表3。另外，由图1、图3和图5所示的MR-t图可以看出，其变化呈曲线关系，故需要对其实验数据进行分析和处理，分别作出-lnMR—t和ln(-lnMR)—lnt的关系曲线图，见图7～图12。

表3 常用的干燥模型及其线性化处理

图7 不同切片厚度下的-lnMR-t关系曲线

图8 不同切片厚度下的ln(-lnMR)-lnt关系曲线

图9 不同干燥温度下的-lnMR-t关系曲线

图10 不同干燥温度下的ln(-lnMR)-lnt关系曲线

图11 不同装载量下的-lnMR-t关系曲线

图12 不同装载量下的ln(-lnMR)-lnt关系曲线

由图7和图8可知，马铃薯片在3、4、5 mm不同厚度情况下，-lnMR与t、ln(-lnMR)与lnt呈正相关，且马铃薯片在3 mm厚度时-lnMR-t关系曲线的斜率最大，说明切片越薄干燥速度越快，3 mm切片干燥速度明显大于4、5 mm切片；在40、50、60 ℃不同干燥温度下，马铃薯片的-lnMR与t、ln(-lnMR)与lnt呈正相关，见图9和图10，干燥温度在 60 ℃时，-lnMR-t关系曲线的斜率最大，50 ℃时的干燥曲线斜率与60 ℃差别不大，40 ℃时的干燥曲线斜率最小，说明50 ℃和 60 ℃温度下干燥速率无较大区别，为避免高温对马铃薯片营养成分的影响，50 ℃的干燥速度更合适；不同马铃薯片装载量的-lnMR-t和ln(-lnMR)-lnt关系曲线图见图11和图12，-lnMR与t、ln(-lnMR)与lnt同样呈正相关，装载量在1 000 g时，-lnMR-t关系曲线的斜率最大，说明装载量越小干燥速度越快。使用Origin将图 7～图12所示的ln(-lnMR)-lnt和-lnMR-t的关系曲线

进行线性回归拟合，得到的回归方程、相关系数、决定系数R2以及各个实验条件下马铃薯切片的有效水分扩散系数如表4所示。

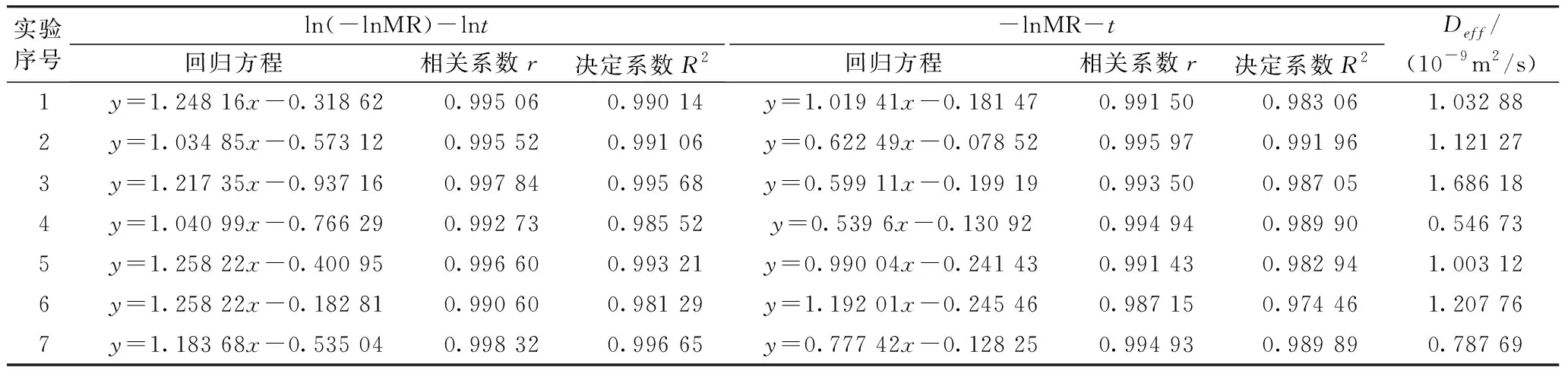
表4 回归方程、相关系数、决定系数及有效水分扩散系数

在马铃薯切片干燥过程中，实验数据在ln(-lnMR)-lnt坐标系内相关系数r变化范围是0.990 60～0.998 32，回归方程拟合优度R2范围是0.981 29～0.996 65；实验数据在-lnMR-t坐标系内相关系数r变化范围是0.987 15～0.995 97，回归方程拟合优度R2范围是0.974 46～0.991 96。由回归方程的相关系数r和方程拟合优度R2的范围可知，实验数据在-lnMR-t和ln(-lnMR)-lnt坐标系内均具有较好的线性关系，因此表3中所示的7种干燥模型中，Lewis和Henderson and Pabis模型的-lnMR与t呈线性，Page模型的ln(-lnMR)与lnt呈线性，这3种模型均适合做马铃薯切片的干燥动力学模型，其余模型均不适合。但进一步对比分析可发现，实验数据在ln(-lnMR)-lnt坐标系内线性拟合精度更高，对ln(-lnMR)-lnt进行指数转换即得Page方程，说明Page模型更适合描述本实验马铃薯切片干燥过程。

由表3知，Page方程线性化得到ln(-lnMR)=nlnt+lnk，其中物料的导热性和水分扩散性等特性通过Page方程中的k表现，待定系数n指物料本身特性对干燥的影响。表4中ln(-lnMR)关于lnt的方程的斜率即为n，截距为lnk；由-lnMR关于t的方程的斜率可求得不同实验条件下的有效水分扩散系数Deff，范围在0.546 73×10-9～1.686 18×10-9m2/s。将实验中的MR-t数据代入Page方程，可以得到各实验条件下的k、n值以及与之对应的拟合优度R2，结果见表5。不同的实验条件对应不同的模型参数值，决定系数R2值在0.993 55～0.999 51之间变化，说明线性回归拟合得到的结果较好，即Page模型可以很好地描述马铃薯切片干燥过程。

表5 不同实验条件下的模型参数值

2.4.2 干燥动力学模型参数值的确定

由于本实验中k，n的值受实验因素条件(切片厚度、干燥温度、装载量)所影响，故可令：

k=a+bX1+cX2+dX3

n=e+fX1+gX2+hX3

式中：X1为切片厚度/mm；X2为干燥温度/℃；X3为装载量/g；a、b、c、d、e、f、g、h为待定系数。使用Origin软件将实验数据代入2个方程中，并进行多元线性拟合，求得方程各待定系数，去除不显著项。得到的回归方程为：

k=0.808 92+0.164 19X1+0.011 78X2-0.000 214 77X3，R2=0.918 94

n=0.631 85-0.021 01X1+0.010 56X2+0.000 032 13X3，R2=0.989 79

回归方程的显著性分析如表6所示，Page模型参数k和n的F值对应的概率值均小于显著性水平0.05，所以方程回归效果显著。因此，可以得到马铃薯切片干燥动力学方程为：

MR=exp[-(0.808 92+0.164 19X1+0.011 78X2-0.000 214 77X3)·t0.631 85-0.021 01X1+0.010 56X2+0.000 032 13X3]

表6 方差分析表

2.4.3 干燥动力学模型的验证

为检验Page模型对马铃薯片热泵干燥过程预测的准确性，选取厚度为3 mm，热泵温度50 ℃，装载量1 500 g条件下进行验证实验，得到水分比(MR)-时间(t)关系曲线。实验中的实测值和根据模型方程得到的预测值之间的关系如图13所示。由图可知，马铃薯片热泵干燥过程中水分比的实测值与Page模型的预测值拟合程度较高，说明Page模型能较准确地描述该干燥过程中马铃薯片的水分变化情况，对马铃薯片热泵干燥过程具有较好的预测作用。

图13 相同干燥条件下水分比实测值与预测值的比较

2.5 正交设计实验结果分析

实验结果及正交极差分析如表7所示。从极差分析表中可以看出，空列的极差值均小于因素列的极差值，故A、B、C各因素的水平效应的差异是存在的。由表分析可知，在切片厚度、干燥温度和装载量3个因素中，切片厚度对干制品的色差(ΔE*)影响最大，其次是温度，装载量对干制品的色差值影响最小，较优组合是A2B2C1；而干燥温度对于干制品的复水比影响最大，其次是切片厚度，装载量对复水比影响最小，较优组合是A2B2C1。在色差值和复水比2个指标中，较优组合均为A2B2C1，因此可确定马铃薯片最佳的热泵干燥工艺参数，即切片厚度3.0 mm，温度50 ℃，装载量1 500 g。在此条件下，干制品的色差值最小，与新鲜样品颜色差异最小，复水比达到最大值，复水性最优，干制品综合品质最佳。

表7 L9(34)正交实验结果与极差分析

3 结论

本研究通过建立动力学模型预测马铃薯片在热泵干燥过程中的水分变化规律，得到描述其规律的Page数学模型：MR=exp (-ktn)，式中：k=0.808 92+0.164 19X1+0.011 78X2-0.000 214 77X3，R2=0.918 94；n=0.631 85-0.021 01X1+0.010 56X2+0.000 032 13X3，R2=0.989 79，方程回归效果显著。验证发现，Page模型的预测值与实测值吻合良好，可用于描述马铃薯片热泵干燥过程的水分变化规律。通过正交实验证明马铃薯片最佳的热泵干燥工艺参数为切片厚度3.0 mm，干燥温度50 ℃，切片装载量1 500 g。实验结果可为热泵干燥处理方式在马铃薯等农产品中的生产应用提供参考依据。

马铃薯片在热泵干燥过程中，热空气作为干燥介质将热量传递给新鲜切片，使其表面的水分汽化，内部和表面之间产生水分梯度差而逐渐除去水分，但在干燥过程中水分子的迁移和扩散、水分相态变化、以及水分状态变化对马铃薯片色泽、质构等品质特性影响的机制尚不清楚，后续可以借助核磁共振等技术手段进一步探究。