基于遗传算法求解的射电望远镜主动反射面的形状调节策略分析

王震，王思懿，王鑫，吴铮

（1.南京信息工程大学 长望学院，江苏南京，210044；2.南京信息工程大学 计算机与软件学院，江苏南京，210044）

0 引言

中国天眼（简称FAST）是我国发明的目前世界上口径最大的射电望远镜[1]，它的主要组成部分包括主动反射面、信号接收系统（馈源舱）等。其中主动反射面是一个可调节球面，由主索网、反射面板、下拉索、促动器等部件构成，反射面板、主索网的连接示意图如图1所示。主动反射面不工作时处于基准态，呈现为一个半径R约300米。

图1 反射面板、主索网的连接示意图

口径约500米的基准球面。当FAST对目标天体进行观测时，底端固定在地面上、沿基准球面径向安装的促动器，通过改变径向伸缩量，拉动连接的主索节点，从而调节反射面板位置，使得主动反射面调节为合成工作面，将来自天体的电磁波经反射汇聚到馈源舱。合成工作面的口径为300米，馈源舱接收平面中心的移动轨迹形成的焦面与基准球面同心，半径差为F=0.466R，天体S的方位用方位角α和仰角β来表示。

结合上述背景，在确定理想抛物面方法的基础上，当天体S位于方位角α= 36.795°，仰角β= 78.169°时，确定此时的理想抛物面，并建立反射面板的调节模型，使得相应促动器在调节后，形成的反射面尽可能贴合得到的理想抛物面。最后，得到理想抛物面的顶点坐标、合成工作面所包含的主索节点的编号、位置坐标，以及各促动器的伸缩量。

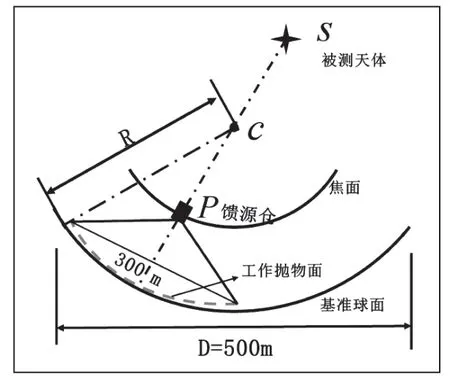
图2 剖面图

1 问题分析

需要找到满足促动器伸缩比在合适范围内，最接近抛物面的合成工作面。原信号入射角并非垂直向下，而抛物面方程在正向为坐标轴方向的情形下，具有最容易求解的形式，因而旋转坐标系，使信号沿z轴射入。主索节点随促动器的伸缩与下拉索的转动，具有高自由度。为了简化求解难度，将主索节点限制在预设的合成工作面上，从而减少了主索节点的自由度。另一方面，主索长度变化不能超过0.07%，直接处理这些几何约束会导致极大的计算复杂度，因而通过将长度约束转化为面积约束，建立由基准球面向抛物面的投影模型。最后，以调整后主索节点到抛物面的距离平方和为优化目标，促动器伸缩极限为约束条件，求得最佳的合成工作面以及对应的主索节点坐标。

2 模型假设

为使建立的模型得到简化，本文进行了以下合理假设：

天文观测中，信号源距离地球十分遥远，可以假设电磁波信号沿直线平行入射到主动反射面。

表1 符号说明

3 主动反射面调节模型

除了需要确定理想抛物面，还根据确定的抛物面，调节与反射面板相连接的促动器的伸缩量，使得信号汇聚效果达到最优状态。

■3.1 坐标系旋转变换

设天体的方位角α为36.795°，仰角β为78.169°，此时，理想抛物面的顶点相比于位于基准球面球心正下方，空间上会偏移一定的角度，方位为( -α,-β)。然而因为大多数情况下，当抛物面的焦点位于z轴上时，抛物面的方程易得，所以需要先进行坐标系的旋转变换，这里，以天体所在方位(α,β)为例，给出变换过程，如图4所示。首先，将(a)中的SC绕z轴旋转θ角，θ= -α，转到(b)中的位置，此时SC处于xCz平面，旋转矩阵为：

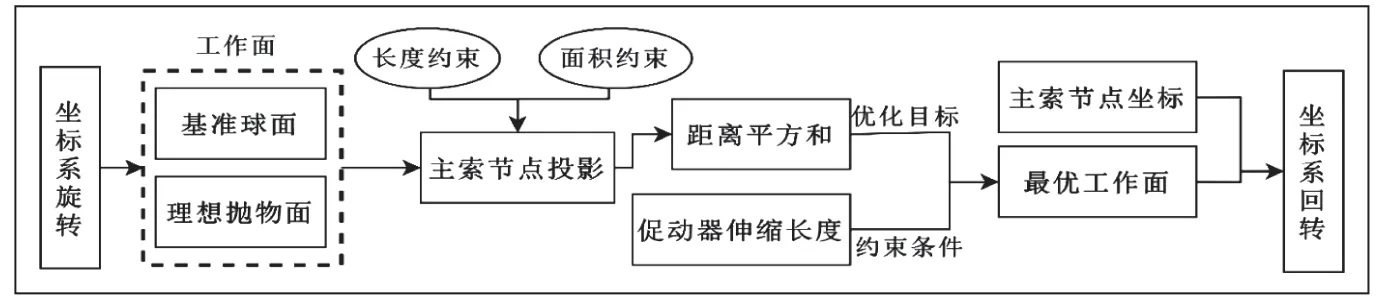
图3 流程图

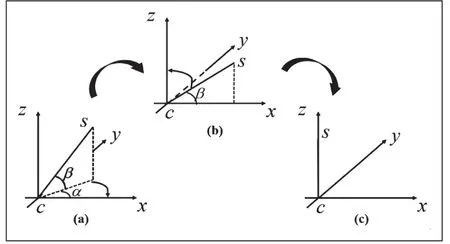
图4 坐标变换过程

接着，将SC从(b)中的位置绕y轴旋转φ角，φ= 90°-β，转到(c)中的位置，旋转矩阵为：

此时旋转结束，SC从最初的方位(α,β)旋转到了方位( 0,90°)，即旋转到了z轴上。两次变换过程的总旋转矩阵为：

将总旋转矩阵应用到坐标系中主索节点，转换为新坐标系下的坐标，并对新坐标根据其到z轴的水平距离，找出水平距离在150m以内的所有点，共有692个，由近及远进行编号，其中D23旋转后的坐标的水平距离最接近顶点。最后，再通过坐标系回转，可以得到原来坐标系中点的坐标。

■3.2 基准球面到合成工作面投影模型

3.2.1 合成工作面方程

下拉索可以任意角度旋转，这使得每个主索节点具有三个自由度，大大增加了求解难度，因此我们假设存在这样的合成工作面，它由基准球面f1(x,y,z):x2+y2+z2=300和理想抛物f2(x,y,z):x2+y2-560z-78109=0面组合而成，所有的主索节点可以完全落于这个面上，方程为：

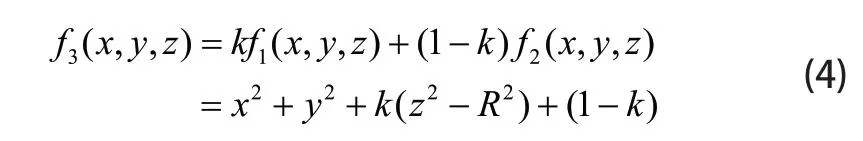
为了保持求解方法的适应能力，令k随坐标变化取不同的值，另一方面，因为基准球面与理想抛物面的模型均关于z轴中心对称，因而同样希望k关于垂直z轴的各个方向同性，最终建立k的函数形式：

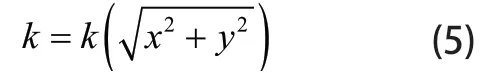
3.2.2 主索投影的长度约束

为了使策略更准确规定相邻主索节点间距离变化幅度不超过0.07%，给了每个主索节点很强的位置约束，利用这种位置约束关系可以进一步降低主索节点的运动自由度。图5给出了因为促动器伸缩导致主索上下位移的示意图，主索距离基准球面的微小位移为Rδ，可以认为下拉索的用力变化ropeFδ与之具有一定的线性关系：

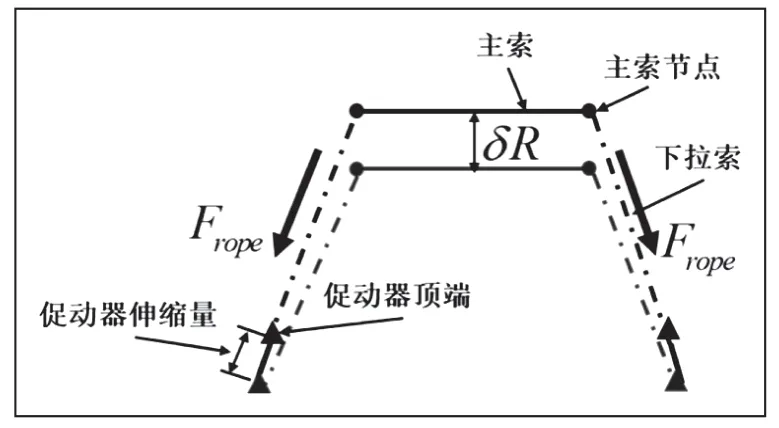
图5 主索下拉图

根据胡克定律，弹性介质受力的微小变化与其形变成正比，假设下拉索的用力变化为主索形变的主要原因，则可以得到如下的关系：

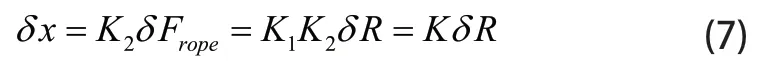
其中，xδ为主索的形变量。

对于主索两端距离基准球面微小位移不同的情形，且认为当两端促动器均下移0.6m时，主索受力最大，达到形变极限0.07%：

3.2.3 基于长度约束的逐点投影方法

基于上述的长度约束建立逐点投影方法，确定合成工作面上各主索节点的位置方案如下。

假设合成工作面上有相邻已知点A(xA,yA,zA)、B(xB,yB,zB), 需求解与两点相邻的另一未知点C(xC,yC,zC)。可以建立如下的约束方程组：

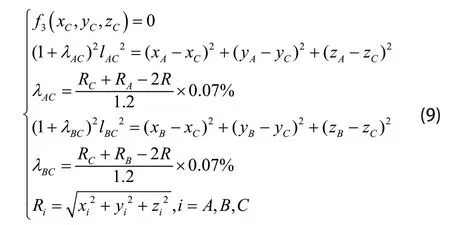
其中BCλ与ACλ分别为BC段主索与AC段主索的拉伸比，BCl与ACl分别为BC段主索与AC段主索的原长。一个合成工作面约束、两个长度关系约束可以完全求得未知点C的坐标。

3.2.4 基于面积约束的逐点投影方法

上述的迭代生成方法对于每个合成工作面可以完全确定其上主索节点的坐标，但是每一次生成点需要求解一组非线性方程，每一张合成工作面需要生成上百个点，计算复杂度非常高，且计算点时虽然可以从中心向边缘依次求解，但微小的偏移会导致误差无限放大，因而并不可行。

鉴于此，需要进一步简化模型，因为基准球面和抛物面由1286个反射面板拼接而成，因而可以将离散面简化为连续面，并且采用面积约束代替长度约束进一步简化约束条件。

因为作为连续面的基准球面与抛物面皆是关于中心轴各向同性的曲面，因而将各主索节点的水平方向坐标转化到极坐标系中，为：

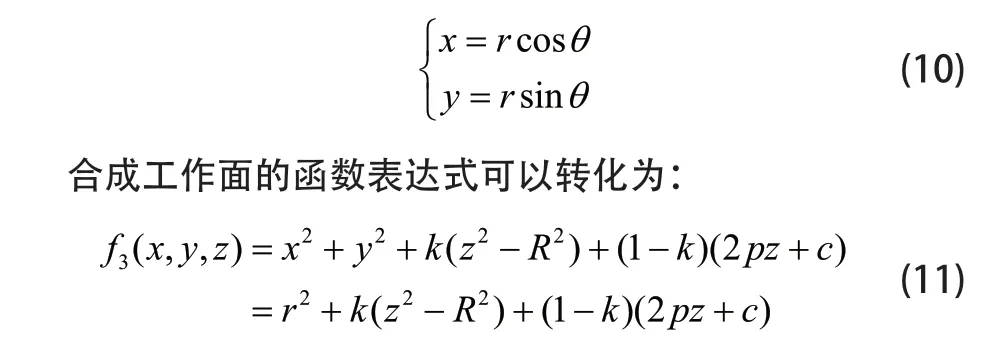
因为连续地合成工作面与基准球面具有各向同性的性质，所以基准球面向合成工作面的投影不会改变坐标方位角θ。基准球面上的坐标 (r0cosθ,r0sinθ,z0)，投影到合成工作面上的坐标为(r1cosθ,r1sinθ,z1)，投影过程如图6所示。

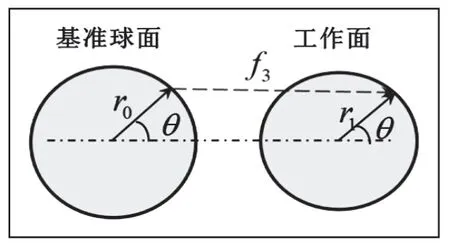
图6 基准球面向合成工作面的投影

为建立0r到1r具体的投影关系，转而考虑基准球面向合成工作面面元间的映射关系。因为主索节点之间的距离变动幅度并不大，各反射面的面积变化同样不大，通过前文所述的投影长度变换，得到合成工作面面元相较于基准面面元的放大比为：

将合成工作面面元面积除以放大比得到与它对应基准球面上的面元面积，对这些面元进行积分。认为水平方向半径在0r以内的基准球面面元的面积与1r以内除以放大比之后的抛物面面元的面积积分相等，得到如下的方程组：

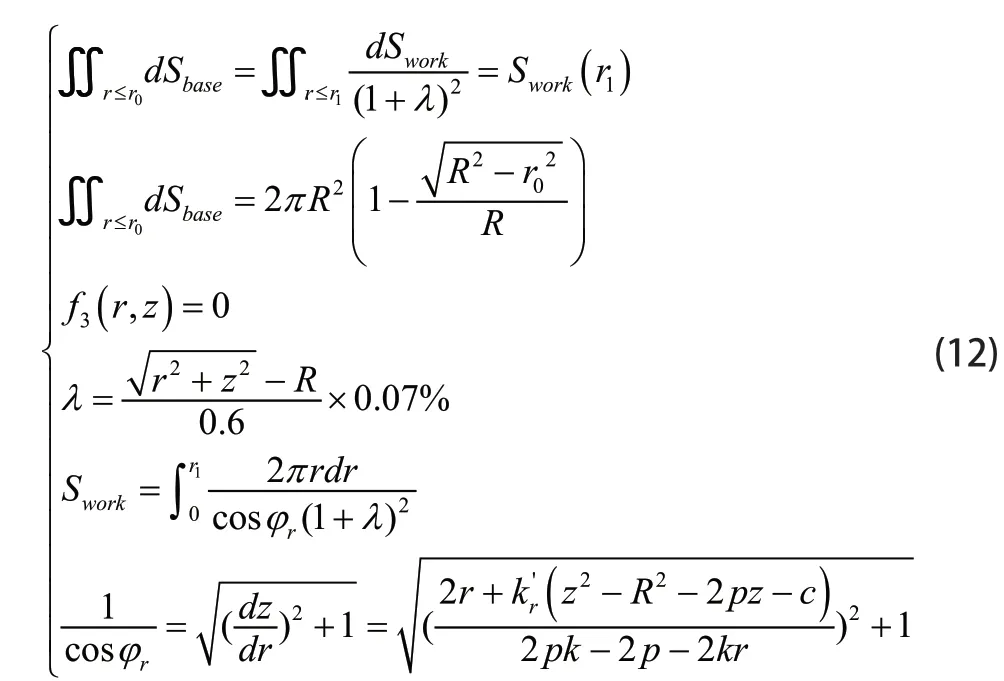
式中，base为基准球面面元，work为合成工作面面元。

dSdS

■3.3 基于投影模型的反射面板调节模型

3.3.1 促动器伸缩量根据官方给的基准态时促动器上端点坐标和促动器下端点坐标，可以解出促动器在基准状态下的初始长度约为1.98m。根据基准态时主索节点的坐标和促动器上端的坐标，即每个节点对应的一根下拉索的长度，范围约为

关于促动器的伸缩量，由促动器伸缩后的长度和初始长度得到伸缩量。促动器伸缩后的长度可以结合下拉索以及主索节点，构成如图7所示的一个长度三角形。图中的

图7 长度三角形

因为促动器伸缩方向不变，故用初始上端点和固定的下端点的坐标，刻画促动器的方向。由于之间会有一个偏移角，设为iφ，可以得到：

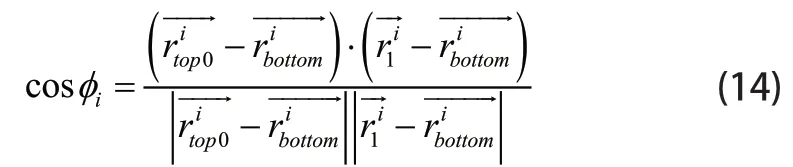
由三角形的余弦定理：

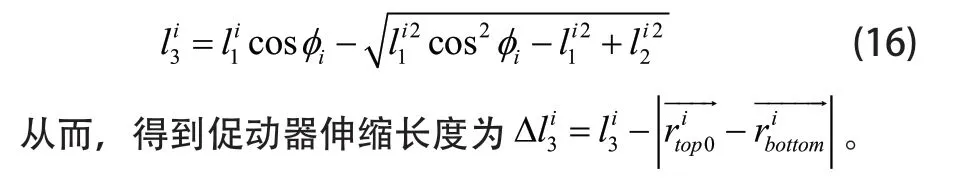
3.3.2 目标优化模型

（1）k为线性函数

一般情况下，k不会是完全的常值函数，因为不同半径处的基准圆面在逼近抛物面时，具有不同的特征，所以需要随着r的变化，在不同坐标处会取不同的值。

令k ar b=+，对于不同的a，可以借助上文中的优化模型，找出最小的b值，即可以得到a值对应的最接近抛物面的合成工作面。为在这些合成工作面中找到最合适的合成工作面，以调节后主索节点与理想抛物面上的点的距离平方和为优化目标，建立改进的目标优化模型：

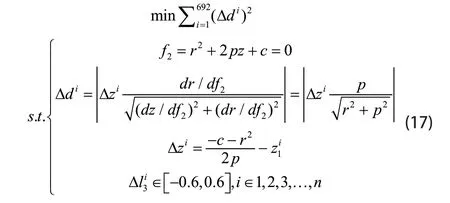
其中，第i个主索节点坐标与理想抛物面的径向距离Δdi是通过结合抛物面法线方向与到抛物面的垂直距离近似求解得出。

■3.4 利用遗传算法求解与分析

（1）k为常数函数

以0.01为步长，遍历k值，画出促动器伸缩量不满足约束条件的主索节点数的变化见图8。从图中可见，随着工作面逐渐接近理想抛物面，但是不满足约束条件的主索节点数也随之迅速震荡增长。而当其经过0.4时，超越约束范围的主索节点数目趋于稳定，并在k= 0.50时，达到满足所有约束条件的最小值，此时的距离平方和147.4469。

（2)k为线性函数

令k=ar+b，其中a与b为搜索变量，搜索区间分别为[-0 .01,0.01]与■■0 .001,1■■，并满足k∈ (0,1■■，需要满足所有约束条件时，距离平方和最小。

由图8可见，随着k的变化，函数具有明显的震荡特征，一般的梯度下降法易陷入局部最优解。另一方面，这是一个多变量单目标优化问题，遍历求解的计算复杂度较高，因而通过遗传算法求解模型，解得距离平方和最小为138.9363，此时a= 0.0014，b= 0.3254。

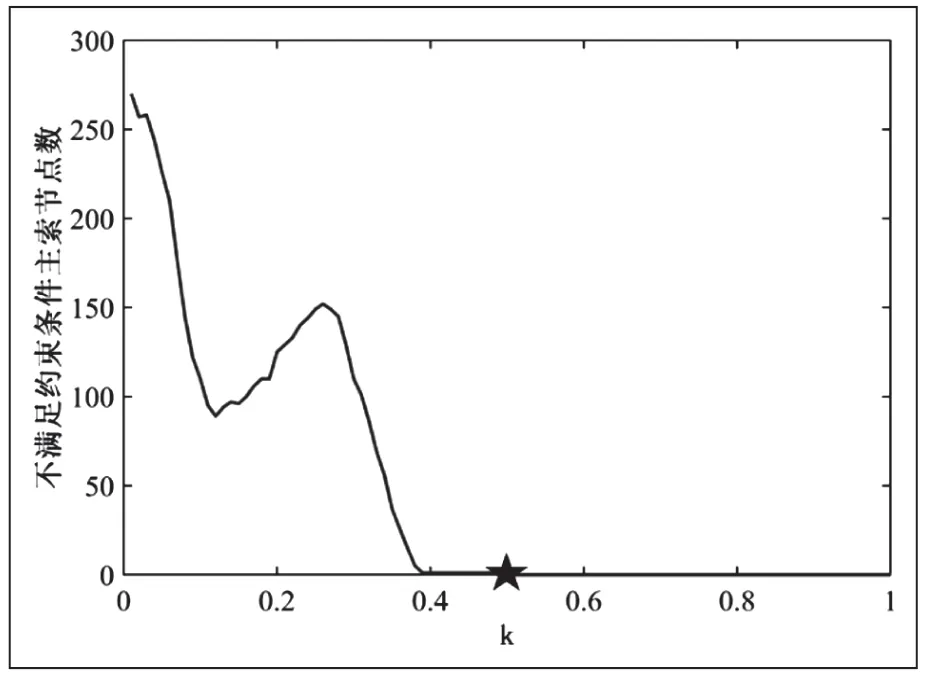
图8 不满足约束条件的主节点数随k值的变化

图9为上文求得的两种k值对应的促动器伸缩量随水平坐标的变化图，以及k为线性函数时促动器伸缩量与k为常值函数时的差值。由图可见，两者之间的差距极为贴近，但是，因为加入了与水平半径成正比的扰动项，求得的主索节点位置变化（通过促动器伸缩量表示）在低值处更低，而在高值处更高，最终使得求出的工作面更贴近理想抛物面。

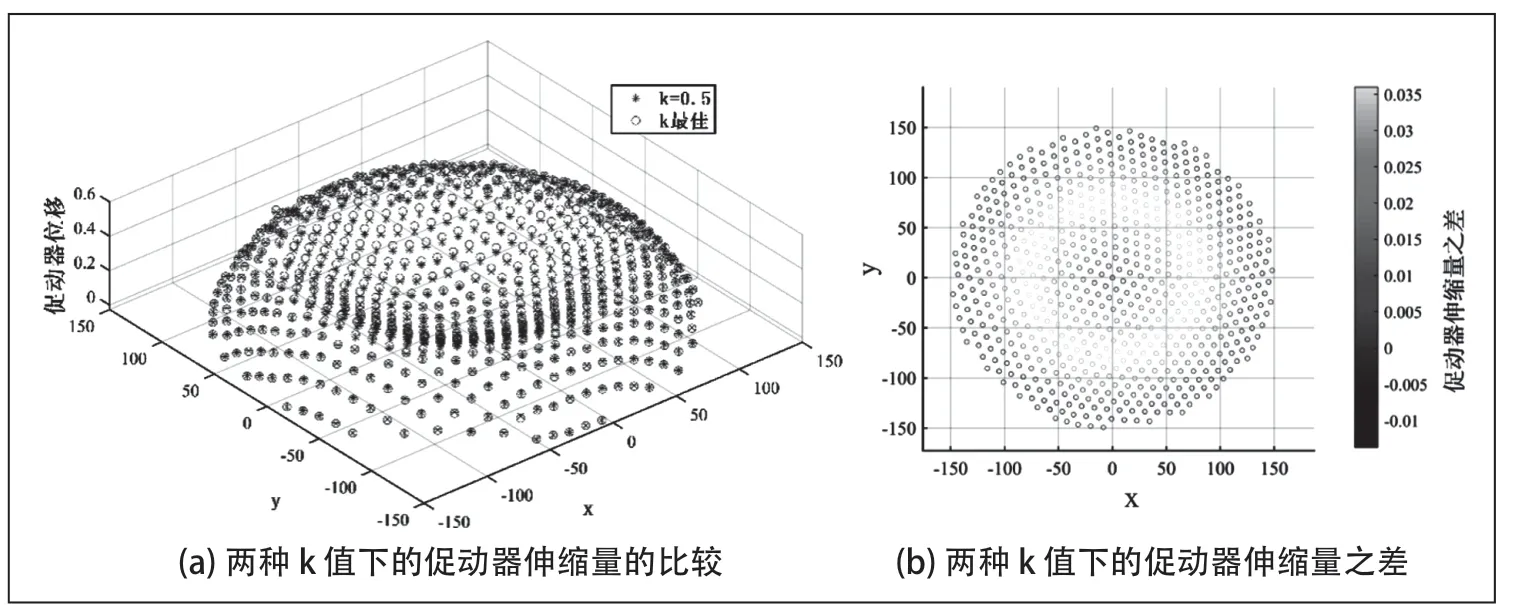
图9

将工作面上的主索节点与促动器伸缩量结合，画出主动反射面上每个主索节点对应的促动器伸缩量，得到图10中的立体图和平面图。结合两张图可以看到，此时的工作面因为观测天体相对于z轴有一定的偏移，所以工作面整体会偏向平面的第三象限。再观察图10(b)，可以发现工作面顶点处的促动器伸缩量几乎为0，说明顶点即周围一小片工作面是非常贴近基准球面的，这与理想抛物面相对于基准球面的位置关系是比较符合的。

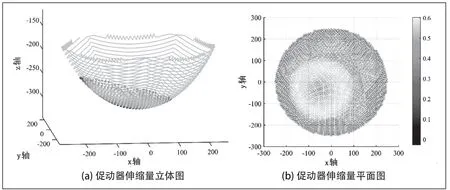
图10

这里给出求得的部分调整后的主索节点坐标和对应的促动器伸缩量，如表2所示。

表2 部分主索节点坐标和连接的促动器伸缩量