空气质量监测数据校准研究

吴 杰，陈 辉

（安徽商贸职业技术学院基础教学部，安徽芜湖 241002）

0 引言

随着人们环境保护意识的提高，空气质量问题受到广泛关注。目前，国内的空气质量网络监测系统主要由国控点和自建点构成。国控点监测数据较为准确，但成本高，布控范围小；微型空气质量检测仪花费小，能够兼顾污染物和环境参数的监测，在自建点得以广泛应用。然而，设备故障、特性漂移、空气交叉干扰等原因导致了数据不可靠。[1]因此，利用国控点对自建点数据进行校准，成为了亟待解决的问题。

近年来，国内外工作者对空气质量预测做了大量研究。周杰等[2]、黄伟健等[3]结合时间序列特征和空间变化特征，对空气质量数据进行了全面预测，提高了预测精度，降低了均方误差。杨涛锋等改进PSO 的ARIMA-SVM 模型[4]通过最大限度提取污染物浓度信息，建立混合核SVM，优化粒子群算法，解决了局部最优解和震荡的问题，取得了良好的预测效果。程蓉等[5]解决了数据过度拟合、算法耗时等问题，在局部空气质量的预测上有一定的优势。李萍等[6]提出基于时间序列的空气质量预测模型，改进了萤火虫算法，降低了预测方差，提高了预测精度，具有较高的稳定性。空气质量数据的预测需要依据观测数据的可靠性，而微型空气质量检测仪监测数据不准确，利用较为精确的国控点数据进行校准，是研究的重要方向。目前，国内监测数据的校准研究还较少。游晋峰等[7]、吕宁宁等[8]建立多元多回归校准模型，利用Pearson 相关系数对两个观测点数据的差异因素进行了分析，得出了污染物与环境因素之间的相关性，但忽略了各因素之间的交叉影响。李艳午等[9]采用偏最小二乘回归，提取各变量之间的主成分，建立空气质量回归方程，解决了数据之间的多重相关性问题。

我们提出零点量程漂移校准模型和BP 神经网络校准模型，并利用具体环境监测数据[10]对模型的效果进行检验，取得了较好的效果。

1 数据处理与分析

1.1 数据处理

通过对国控点和自建点数据分析，我们发现部分数据分布异常且游离于主要数据之外。为提高分析的可靠性，我们剔除该部分数据。

鉴于国控点数据主要为整点数据，为保证数据的时间序列性和预测的精确性，我们以整点时刻Ts(s=1，2，...)为中心，利用线性拟合，建立国控点整点附近的数据库，运用相同方法，在自建点数据中拟合出与国控点数据相对应时刻的观测值。

1.2 数据分析

以Ts(s=1，2，...)为横坐标，绘制出国控点与自建点 PM2.5、PM10、CO、NO2、SO2、O3观测数据的对比图，如图1 所示。

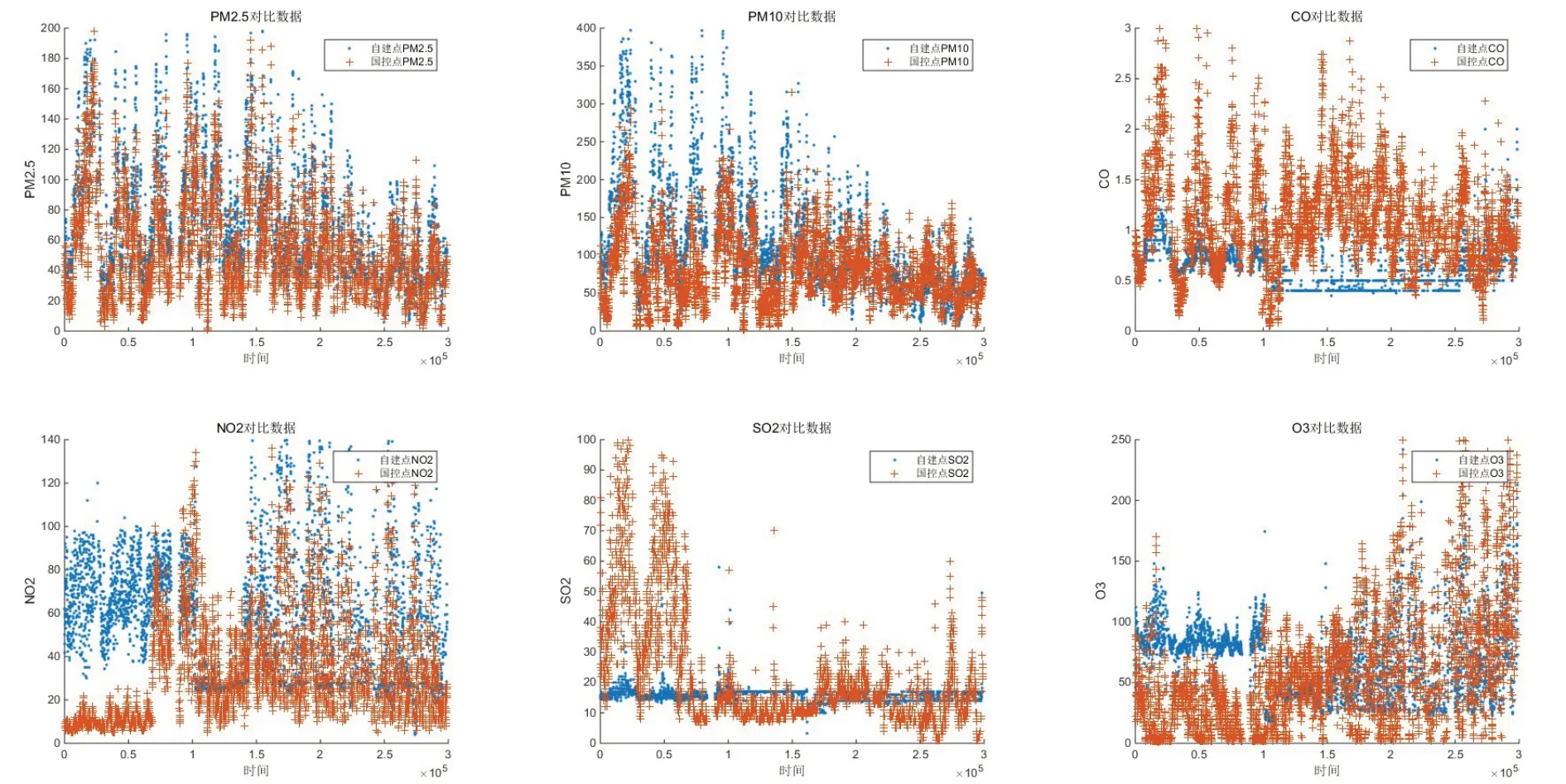
图1 国控点与自测点观测数据对比图

通过对比，国控点和自建点的PM2.5、PM10相关性显著。

以自建点数据为横坐标，国控点数据为纵坐标，绘制出对照图，如图2 所示。

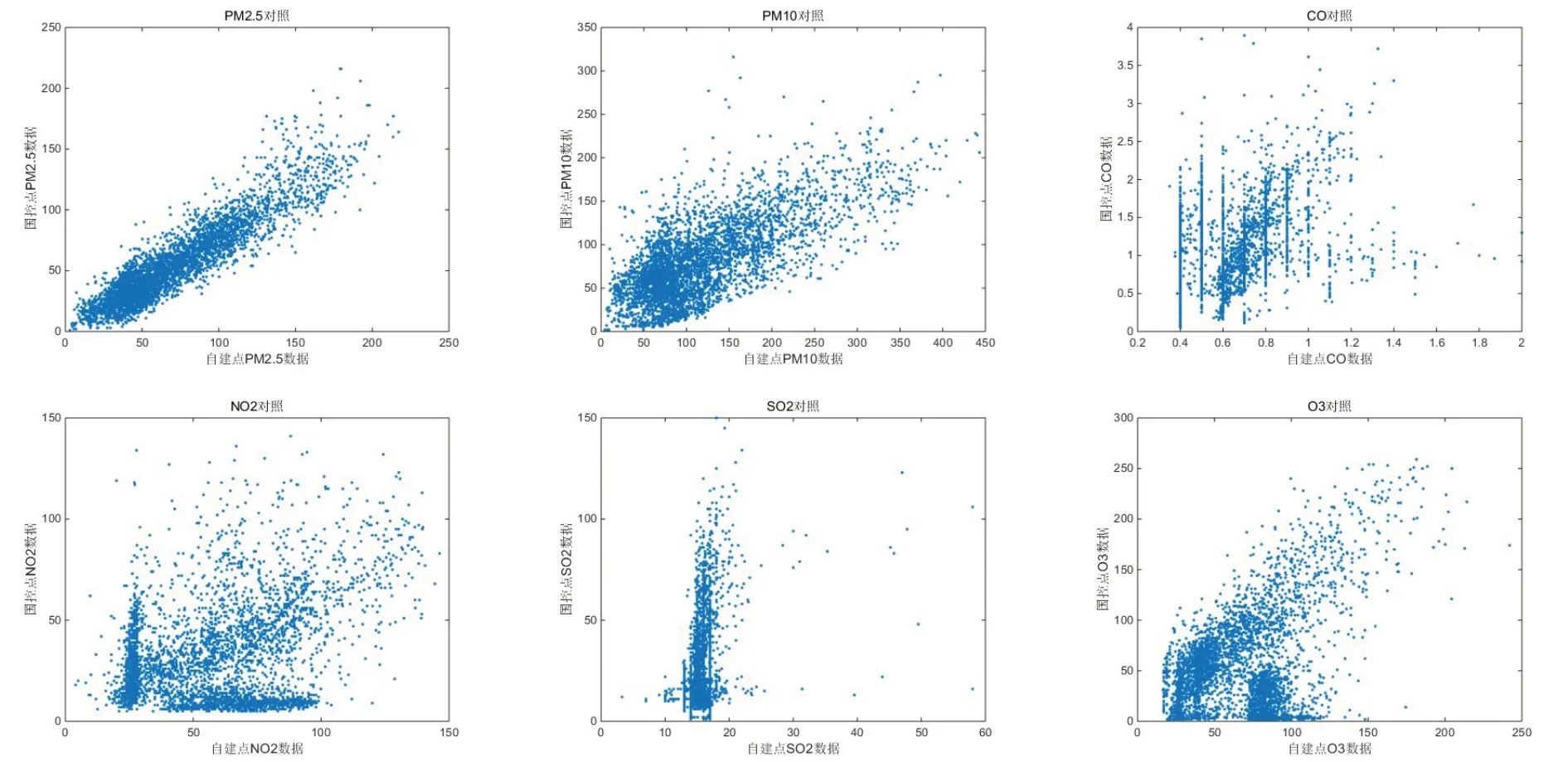
图2 国测点与自建点数据对照图

PM2.5 和PM10 的对照图在直线y=x 附近。计算出它们之间的相关系数，国测点与自测点PM2.5 的相关系数为0.9162，正相关显著；PM10的相关系数为0.7134，正相关较强；O3的相关系数为0.43，正相关性较弱；其余污染物之间相关性不强。

PM2.5 和PM10 是粉尘污染，属于物理属性，具有较好的稳定性，检测数据进行了漂移，可以通过零点和量程漂移修正进行校准；CO、NO2、SO2和O3是化学污染物，需要通过电化学反应进行检查，而化学反应又跟温度、湿度、降雨等环境因素相关，检测数据与环境之间呈现复杂的非线性关系，与相关研究结果相吻合。[11]

2 零点量程漂移校准模型

2.1 零点漂移与量程漂移

首先对污染物PM2.5 和PM10 的数据进行校准。利用环境监测数据[10]，计算出两观测点PM2.5 和 PM10 误 差 分 布 。

误差数据集中在x 轴上方，监测数据产生了零点漂移。

记 i(i=1，2，···，11)分别表示 PM2.5、PM10、CO、NO2、SO2、O3、风速、压强、降水量、温度和湿度，X=（X1，X2，···，X11）为自建点污染物观测数据矩阵，Y=（Y1，Y2，···，Y6）为国控点污染物观测数据矩阵。计算自建点数据在相邻整点时刻附近观测值的极差Ds，即

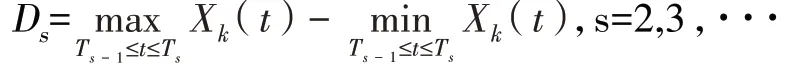
PM2.5 和PM10 量程有轻微减小的趋势。综上所述，经过适当的零点和量程漂移修正后，可以对部分数据进行有效的校准。

2.2 零点量程漂移校准模型

设观测值Xi是由实际值X̂i发生零点漂移Xi0和量程漂移Hi得出，则Xi=HiX̂i+Xi0，可得校准值为

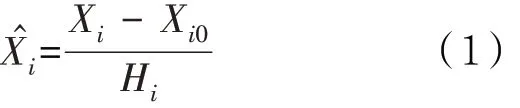
根据零点漂移和量程漂移特性，设

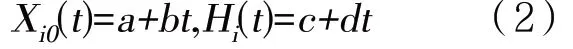
则整点Ts时刻自建点数据的零点和量程漂移校准值据此，建立最小二乘拟合模型如下：

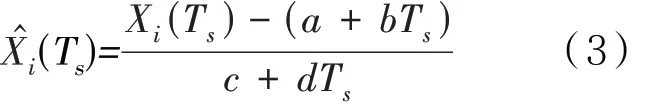
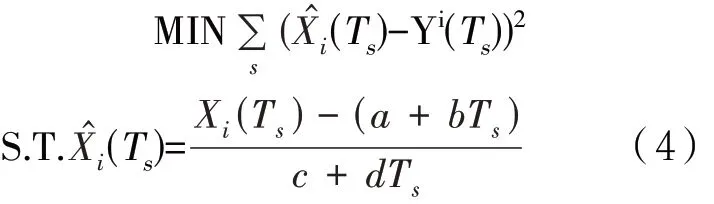
其中Yi(Ts)为整点Ts时刻国控点数据。

对PM2.5、PM10 数据进行拟合，得出零点量程漂移校准模型，对应的参数和均方误差如表1 所示。

表1 零点量程漂移校准模型求解结果

利用校准模型对自建点数据进行修正，得出 修正数据与国测点数据对比图，如图3 所示。

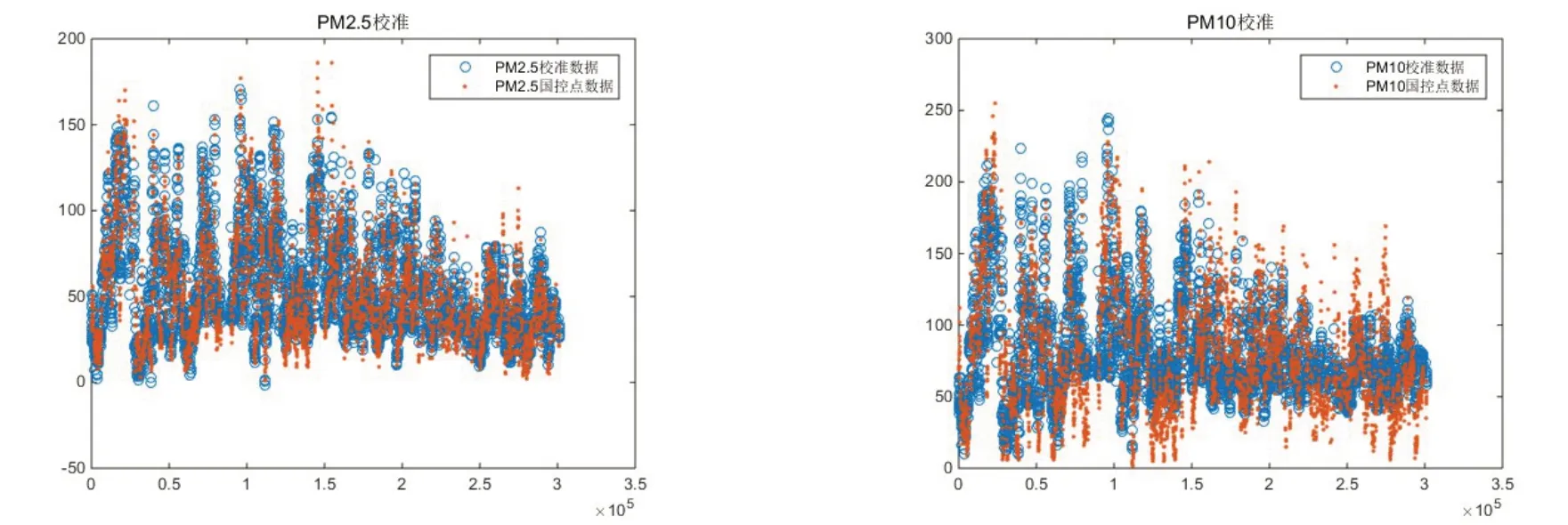
图3 零点和量程漂移修正效果图

将图3 与图1 对比，发现修正数据与国测点数据大部分重合，拟合效果较好。对应修正后的误差如图4 所示。

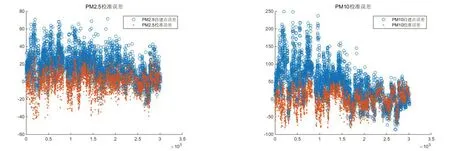
图4 零点和量程漂移修正误差效果

观察图4，发现修正后误差围绕x 附近分布，且误差幅度显著减小。作出修正后的数据对照图，如图5 所示。

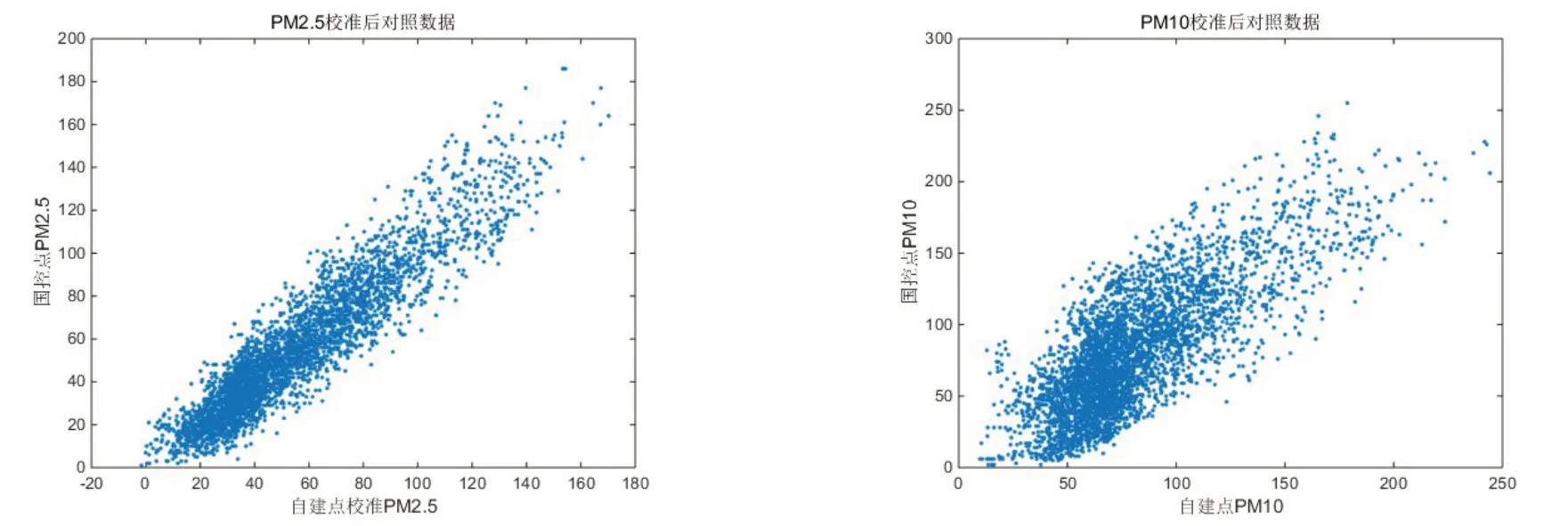
图5 零点和量程漂移修正对照图

PM2.5 自建点校准数据与国控点数据紧紧围绕在直线y=x 附近，校准效果较好。PM10 自建点校准数据与国控点数据围绕在直线y=x 附近，也取得了较好的校准效果。

运用类似方法，对 CO、NO2、SO2、O3进行零点与量程漂移校准，具体校准结果见表2。

表2 零点量程漂移校准模型校准结果

由表2 可见，CO、O3自建点得到了一定的修正，但仍与国控点数据有较大差距；NO2、SO2自建点数据经过模型修正，取得效果甚微。这与上节的分析相吻合，它们属性化学污染物，仅通过零点与量程漂移进行校准是不够的，还需要考虑到其他环境因素。

3 BP 神经网络校准模型

BP 神经网络是一种按误差逆传播算法训练的多层前馈网络，有很强的非线性映射能力。其主要由输入层、隐含层和输出层构成，且网络的隐含层可根据具体情况设定，灵活性很大，为了降低网络的复杂性，仅设定一个隐含层。[12]对于隐含层神经元数目k 的确定，目前没有严格的规

其中，m 为输入层神经元数，n 为输出层神经元数，δ ∈[1,10]为整数。

鉴于自建点观测数据受其他环境因素影响较大，且观测数据之间线性相关性不强，环境因素之间的交互作用难以显化，因此我们可以通过BP 神经网络学习这个隐藏的特定关系，进而修正自建点的观测数据。具体步骤如下：

步骤1：对数据进行归一化处理，将自测点观测数据X=（X1,X2,...,X11）和整点时刻T 作为输入层，国测点观测数据Y=（Y1,Y2,...,Y6）为输出层，建立具有12 个输入变量和6 个输出变量的BP 神经网络，如图6 所示。

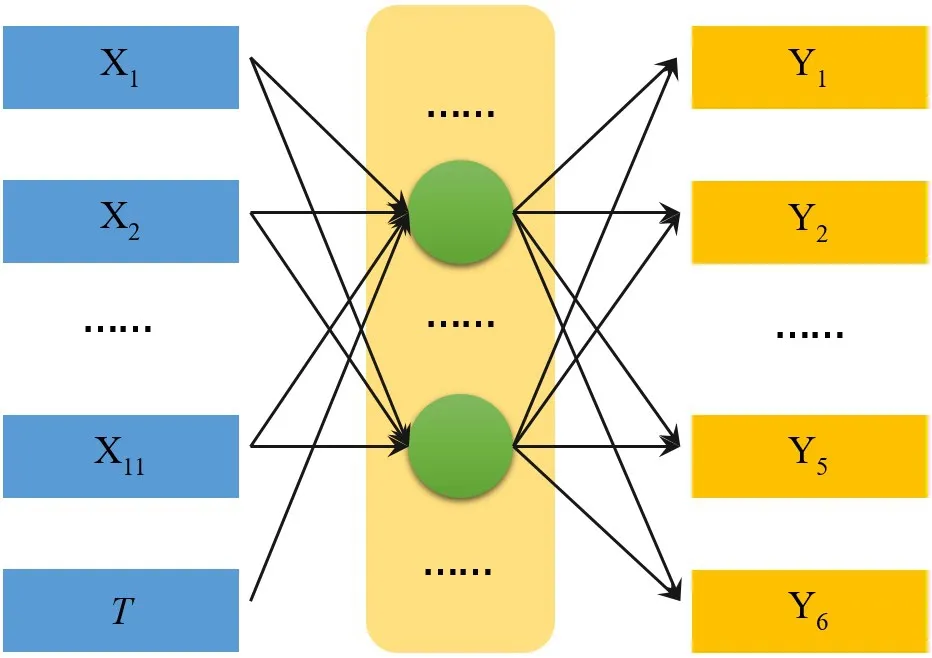
图6 BP 神经网络

步骤2：初始化输入层、隐含层、输出层之间的连接权重矩阵A,B 和隐含层、输出层的阈值矩层输出矩阵H 和输出层输出矩阵O：

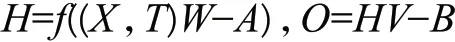
步骤3：计算网络预测误差e=Y-O。若误差e已达到预测精度，直接输出结果；若误差e 未达到预测精度，更新网络连接权值矩阵和节点阈值矩阵[14]，返回步骤2，重新训练。

利用MATLAB 神经网络工具箱进行求解，得出计算结果如表3 所示。

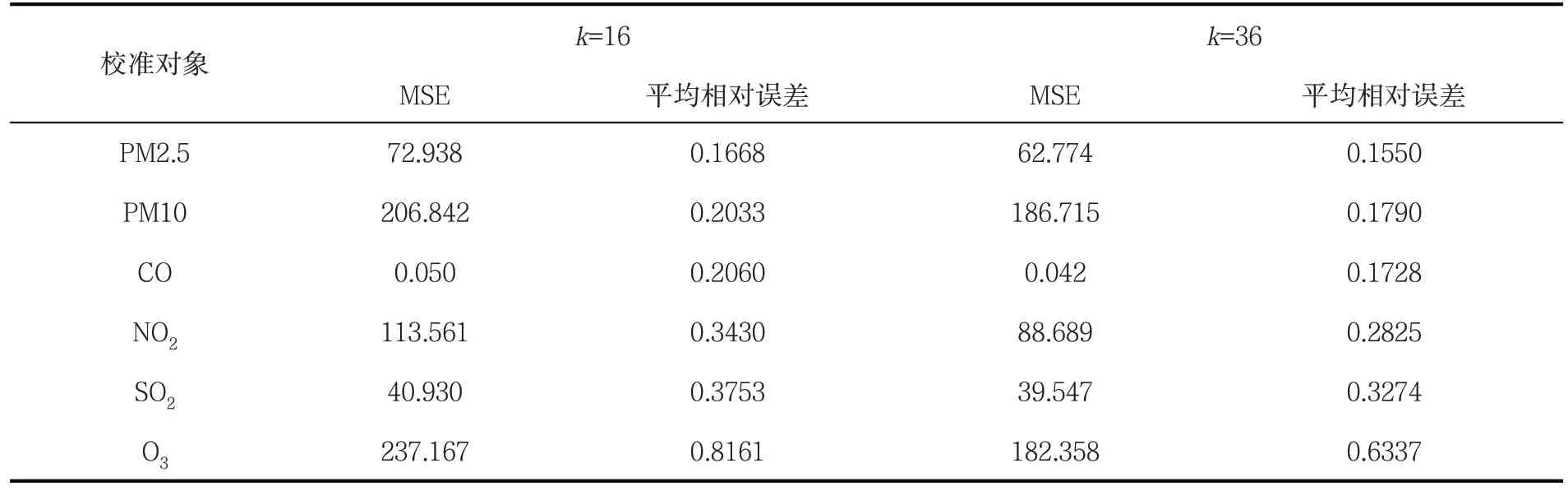
表3 BP 神经网络拟合校准结果

由于数据量较大，通过训练发现，适当提高隐含层的神经元个数，可以取得较好的拟合效果。对比表 1 和表 2，PM2.5、PM10 的均方误差和平均相对误差都变小，CO、NO2和SO2均方误差和平均相对误差较小，可见，BP 神经网络统筹考虑了不同因素之间的交互作用，经过充分学习训练后，获得更好的校准效果。而对于O3的校准，效果不理想，通过不断调整隐含层的个数，仍未取得较好的效果，与BP 神经网络的高拟合效果违背，这可能是监测数据出现异常所致。

绘制出BP 神经网络校准数据与国测点数据对比图，如图7 所示。除了O3的后半段数据，其余校准数据与国测点数据重合率较高，说明通过BP 神经网络训练，机器学习到了各污染物之间的特定关系，取得了较好的校准效果。

图7 BP 神经网络拟合对比图

由此可知，BP 神经网络校准误差数据紧靠x轴上下波动，且呈现出正态分布，表明BP 神经网络已经充分利用已有信息，误差得到有效控制。

将BP 神经网络校准数据与国测点数据进行对照可知：对照数据紧密分布在直线y=x 附近，说明校准数据与国测数据已经高度吻合，校准效果显著。

4 结语

基于监测数据之间隐含的零点漂移和量程漂移特征，我们建立零点量程漂移校准模型，利用线性回归分析理论进行拟合，不仅对自建点数据进行了一定的修正，而且揭示了环境因素对监测数据复杂的影响规律。基于数据间的多重相关性，我们建立BP 神经网络模型，通过大规模的训练，学习数据之间复杂的非线性关系，得出了各污染物数据校准模型。多种模型循序渐进、逐层深入，取得了较好的校准效果。

零点量程漂移校准模型建立了各污染物之间校准函数，模型直观，但对部分污染物校准效果不明显，尤其对气态污染物的修正，发挥作用不显著。BP 神经网络模型取得了较好的校准效果，但各因素之间的影响规律和交互作用缺乏可读性。因此，建立更精细的非线性回归模型是我们未来改进和完善的一个方向。