基于遗传算法的Delta 并联机器人机械结构工作空间逆解研究

张广祥，李玉爽，查子延

（1.芜湖职业技术学院信息与人工智能学院，安徽芜湖 241003；2.芜湖职业技术学院智能制造学院，安徽芜湖 241006；3.南京理工大学机械工程学院，江苏南京 210094）

0 引言

随着工业自动化、智能化的发展，在生产制造中人工无法完成或工作效能较低的情况下，工业机器人发挥着越来越重要的作用，正在逐渐替代人工体力劳动。目前并联机器人的主要特点是质量轻、速度快、精度高和稳定性高，在提高工作效率的同时，其结构也比较稳定，能够在不同环境下进行作业。并联机器人现已广泛应用于食品医疗、物流分拣等领域。在廉价劳动力逐渐减少、人口红利逐渐削弱的时代，采用并联工业机器人替代人工进行生产作业，可以提高企业的生产效率、有效降低企业人工的劳动成本。[1]

1 并联机器人工作空间分析

并联机器人的逆运动学研究分析主要是根据动平台位置坐标求解驱动关节角度的变化，当一定的约束关系在机器人的各结构上设定后，其动平台中心所能够企及的范围就构成了工作空间。机器人工作空间是评估机器人机械运动性能的一项关键指标[2]，对于工作空间的分析和计算是设计研究并联机器人的重要组成部分。

1.1 建立尺度综合目标函数

尺度综合是指在给定工作空间的条件下求解未知的机器人结构特征参数尺寸，旨在使其结构运动性能达到最佳。已知Delta 并联机器人工作空间∅1200 ×300 mm，需要求解以下参数：（1）主动臂长度 L1；（2）从动臂长度 L2；（3）动静平台半径差e；（4）工作空间上极限位到静平台距离 H。建立向量P =[L1，L2，e，H ]T，使得根据条件已建立的函数值最小，即minF(P)，从而求得尺度综合参数的最优解。

1.2 尺度综合主函数

可达工作空间是指动平台上的点在整个机构进行最大限度运动时所能到达的点的集合，而设计工作空间是指机器人在实际应用场合或需求空间下对其所限定的工作空间。由对工作空间的分析可知，要想使机器人结构满足原始条件，可达工作空间要大于设计工作空间。在设计工作空间上选取八个点Q1～Q8，保证可达工作空间包含这八个点即满足要求。假设这八个点到可达工作空间表面的距离为h，h 数值越小表示空间越接近，利用极限思想可将问题转化为：求取h 最小值。

定义主函数

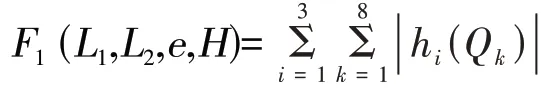
设计工作空间内接底面边长均为a、高为b的长方体上八个顶点的坐标如图1 所示。其中四边形A0B0C0D0对角线长度为设计工作空间的圆柱底面直径R，长方体高度为设计工作空间高度。

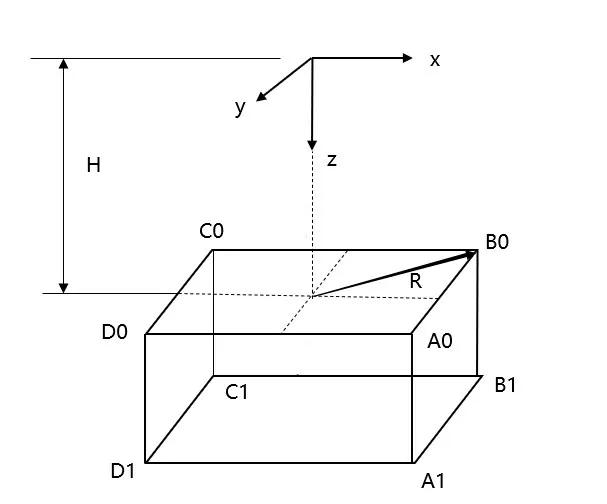
图1 设计工作空间坐标图

当hi＜0 时，设计工作空间任一点P 位于可达工作空间内部；当hi＞0 时，点P 位于工作空间外部；当hi=0 时，点P 在工作空间的边界上。若设计工作空间上的八个点都在工作空间范围内[3]，则有主函数：

1.3 基于空间点位置的惩罚函数

如果设计工作空间上的部分Qk点在可达工作空间范围之外，则不符合机器人结构的设计要求，为保证所有的点都包含在空间内，则定义第一个惩罚函数：

其中，

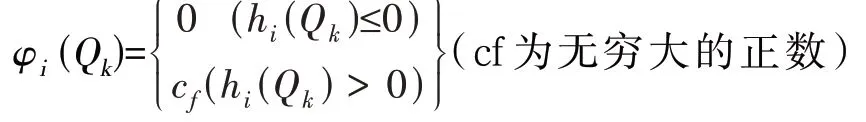
1.4 基于机械结构运动性能的惩罚函数

F1 和F2 两个函数只能保证结构满足设计工作空间要求，但要使机械结构保持较好的运动性能，则需要考虑其运动性能指标。为此，我们通常选用雅可比矩阵J 的条件数T。当T＜5 时，机械结构具有较好的运动学性能；当T＞5 时，其运动性能变差，甚至出现奇异位形。现引入运动性能指标雅可比矩阵条件数T=cond（J）。

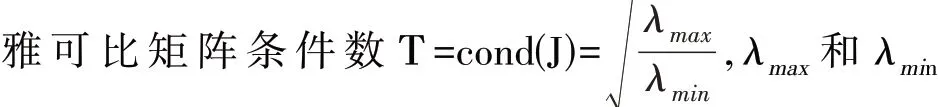
分别是其最大的特征值和最小的特征值。

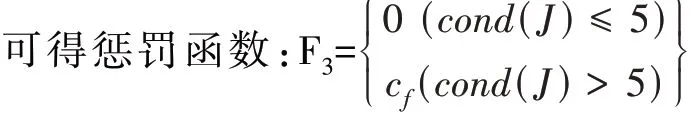
2 基于遗传算法的最优值求解

在经过进化、基因突变和自然选择之后，种群里最能适应生存环境的物种会逐渐出现。将这种生物学遗传方式延伸至数学分析上，类比于自然选择而对实际应用问题进行转化，在生成初始种群之后，我们需要计算其适应度数值并对每个个体的环境适应度进行评估，然后判断其是否符合需求。该种群经过交叉组合、变异等操作过程，新的种群得以产生，而后我们对其进行新一次的适应度评估，最后可以寻得最优结果。根据适者生存的理念，我们反复进行上述操作，直至对环境适应度较高的种群产生。[4]

2.1 基于遗传算法的程序

在并联机器人尺度综合问题的分析和计算中，需要求解四个特征参数 L1、L2、e、H 及其对应遗传算法中种群的四个个体。这四个参数不断交叉、变异，产生新的一组参数，我们通过计算目标总函数F=F1+F2+F3的值来选择种群。此算法在进行一定迭代之后，最优解就会产生，其优化过程如图2 所示。

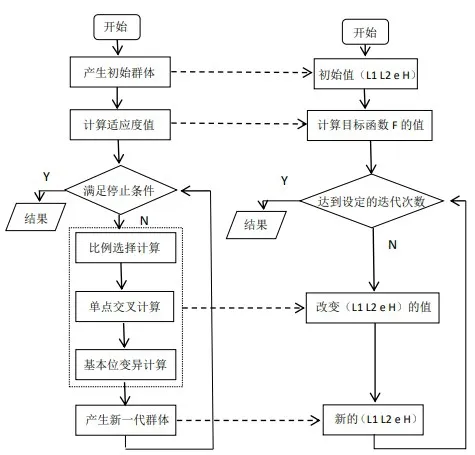
图2 基于遗传算法的综合流程图

2.2 遗传算法的参数设定

遗传算法的计算是利用MATLAB 的“Optimization Tool”中的“Genetic Algorithm”算法进行尺度综合计算的，需要设定其参数，且为避免种群早熟，需要按一定规则进行选取，具体规则如下：（1）种群规模：如果规模太小，就会出现近亲交配，导致有效基因缺失；规模太大，会使得结果难以收敛。一般建议取值为0～100。（2）变异概率：如果概率太小，会引起多样性下降得太快，造成有效基因的缺失；概率太大，虽能保证基因多样性，但高阶模式被破坏的概率也随之增加。一般建议取值 0.0001～0.2。（3）交配概率：概率太大，则容易破坏有利模式，错失最优个体[5]；概率太小，则无法保证种群更新。一般建议取值0.4～0.99。（4）进化代数：如果代数太小，结果不容易收敛；代数太大，则种群早熟不可能收敛。一般建议取值10～500。

所选取各参数如表1 所示，各参数取值范围如表2 所示。

表1 遗传算法参数

表2 变量取值范围

4 个变量取值范围设定为[0 0 0 0]～[1000 1000 1000 1000]，将表1 遗传算法参数输入到MATLAB 的“Genetic Algorithm”计算界面，依据函数进行计算，运算结果如表3 所示。

表3 最优尺寸参数

由运算结果可知，动静平台半径差为160 mm，考虑到静平台上需要一定空间安装电机支架以及减速器等部件，所以动平台半径的取值可初步考虑为90 mm，静平台半径为250 mm。

3 工作空间绘制

我们根据运动学模型编制MATLAB 程序，即在已知主动臂、从动臂、静平台和动平台尺寸的条件下，通过MATLAB 软件进行编程并运行相应程序，绘制出了3 个工作空间视图，如图3、图4和图5 所示。

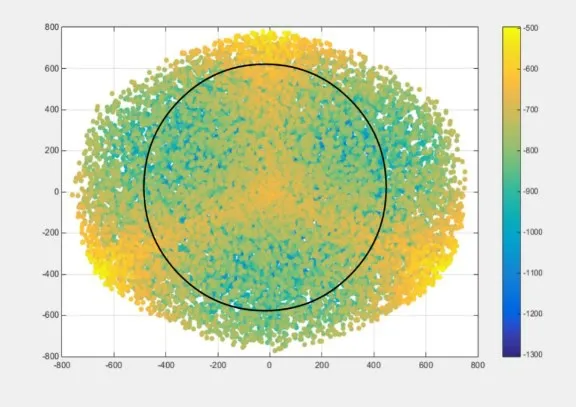
图3 工作空间XY 平面视图

图4 工作空间XZ 平面视图

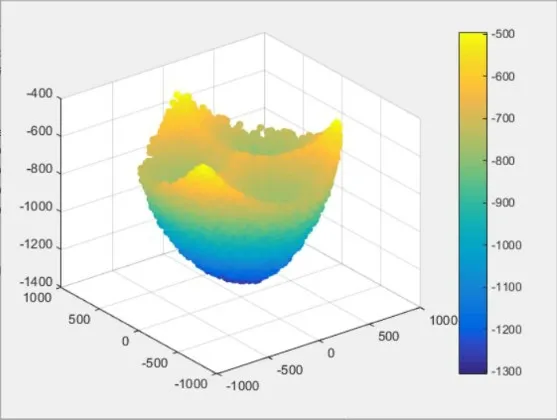
图5 机器人工作空间

由图3、图4 和图5 可知，所设计机器人的可达工作空间为一椭球形状，所要求的设计工作空间包含在该设计结构的可达工作空间范围之内，该机械结构尺度综合参数值为：( )L1,L2,e,H =(370,950,160,900)，满足工作空间的要求。

4 结论

并联机器人的尺度综合设计是机器人设计研究过程中的重要部分，其工作空间逆解的研究，对于提高机器人的运动精度和运动性能具有重要意义。我们利用遗传算法优化计算，并得到了尺度综合参数的最优解。另外，工作空间视图的绘制也验证了遗传算法计算结果的合理性。[6]遗传算法的引入，提高了并联机器人机械结构设计尺寸的精确度，优化了并联机器人的运动学和动力学性能。