指向高阶思维的圆锥曲线解题教学
2022-11-24滕诗媛浙江省温州市第八高级中学325000
滕诗媛 (浙江省温州市第八高级中学 325000)
圆锥曲线是高中数学知识中的重要内容之一,也是高考的一个高频考点,往往出现在选择或填空题的靠后位置和大题的倒数第二题,其难度和重要程度不言而喻.圆锥曲线主要考查学生的直观想象、数学运算和逻辑推理等核心素养,难点在于计算量大和几何条件代数化.
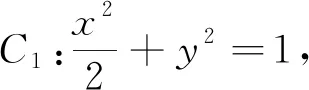
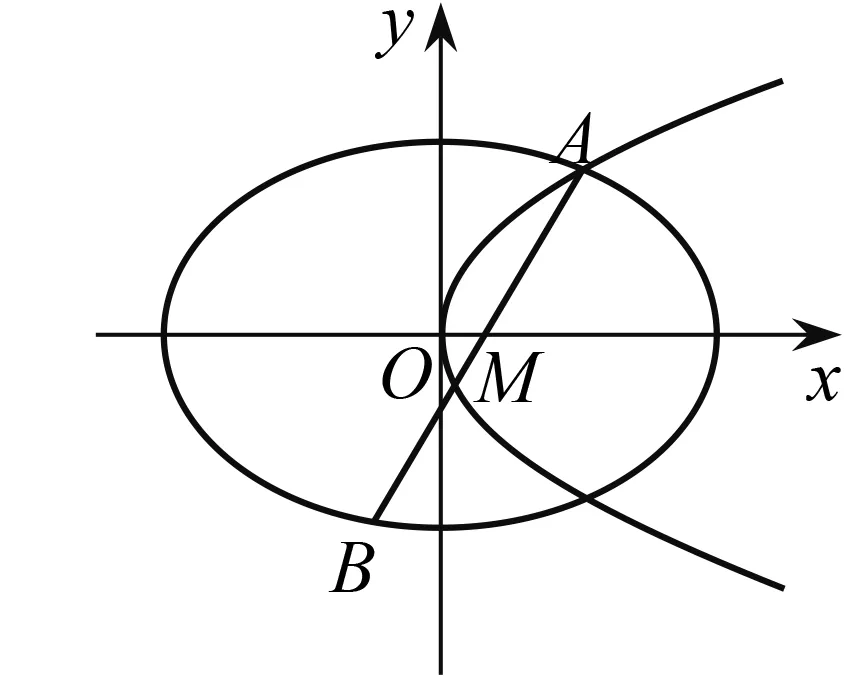
图1
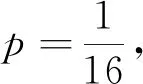
(2)若存在不过原点的直线l,使得M是线段AB的中点,求p的最大值.
本题的第(1)题比较简单,本文重点对第(2)题进行研究.学生拿到题目按照以往的惯性思维进行解题:设点A(线)、联立(抛物线和椭圆方程)、建立目标函数求最值[1].解题思路自然,但解法繁琐,学生没有足够的时间将题目解完整,甚至没办法将目标函数与已知条件联系起来.究其原因是学生未能思考问题本质进而形成自己的解题策略,而教师也往往停留在常规解题方法进行教学,没有分出时间与精力处理学生这一个性化问题.
布鲁姆教育目标分类原理将认知过程分为记忆、理解、应用、分析、评价、创造六个维度[2].以 本题而言,考查的是学生逻辑思维能力(即能正确领会题意,明确解题目标,能寻找到实现解题目标的方向和合适的解题方法,对应应用与分析目标),运算求解能力(即能根据法则、公式进行正确运算变形,根据问题的条件和目标,寻找多种途径,设计较为适合的方法进行运算、变形,对应应用与评价目标)和综合应用能力(即能对具体问题陈述的材料用数学语言正确地表述,用所学的数学知识、思想和方法解决问题,对应分析、评价以及创造目标).对照布鲁姆六大认知能力,这道题乃至这类题目的解题思维显然属于后三种的高阶思维.在此类题目的解析过程中,几何条件与代数表达进行互化无疑是引导学生形成高阶思维的能力载体,因此如何引导学生利用已有几何性质来分析与比较解题方法并将计算简化、将几何条件与代数表达进行互化成了教师必须研究的问题.
1 溯本清源,理清学生思维症结
笔者根据布鲁姆六大认知目标,对本题进行能力知识二维目标的编码分析,形成了问卷,试图通过学生答题结果与问卷调查的对应分析,找出学生“卡脖子”的具体原因,进而提出对应的解决方案.
问卷的问题大致设置如下:
1.本次考试你的得分为分.
2.第21题你的得分为分.
3.第(1)题若未得满分,你失分的原因是( ).
A.抛物线定义忘记了B.计算出错
C.其他
4.为了建立目标函数,第(2)题你选取的自变量是( ).
A.k(直线l的斜率)B.点A坐标
C.m(直线x=my+t) D.其他
5.第(2)题若未得满分,你失分的原因是( ).
A.设出直线方程,与椭圆联立后不知道该怎么做
B.用韦达定理得到点M,B坐标后,算不下去了
C.运算过程出错,导致后面做不下去
D.想利用抛物线方程把点M和A坐标表示出来,有思路,不会算
E.想利用M是中点,用点差法转化为斜率问题,没算出答案
F.无从入手
G.其他
6.在解决这道题的过程中,你认为自己还存在哪些问题( ).
A.椭圆抛物线的几何性质不熟练
B.运算能力不强
C.自变量选取和目标函数的判断
D.动抛物线问题识别不出来
E.解题时,不会比较方法优劣
F.其他
问卷的第1题和第2题统计学生整卷和第21题的得分情况,区分学生水平层次,结合问卷的问题设置,将不同水平学生的失分原因进行区分.学生水平与得分情况成正相关,整卷得分在80分以下的学生第21题的第(2)题得分很低,这部分学生基本属于事实性知识和概念性知识没有掌握,比如忘记抛物线性质,中点条件用不起来,是记忆、理解问题.
参照布鲁姆六大认知目标,分解学生答题过程,问题3~6罗列了学生可能出现的错误、可能会用的解题方法以及存在的问题,试图对照错因与解题方法找出学生在程序性知识和元认知知识上存在的问题.统计学生第(2)题失分原因,如 表1所示.
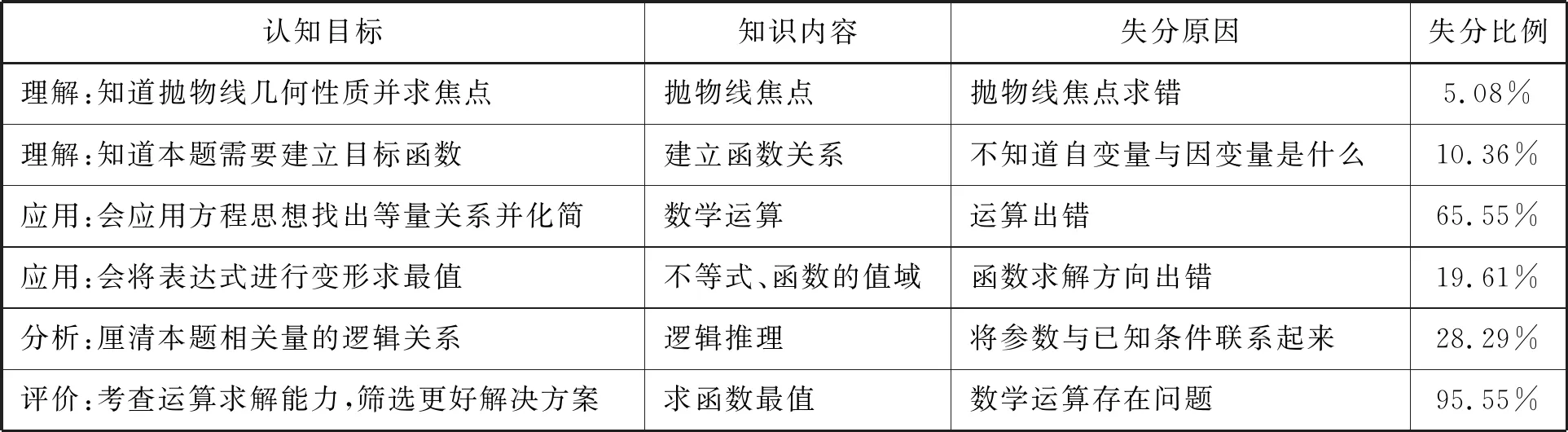
表1 布鲁姆认知目标下学生解题失分原因分析表
由表1可知,大部分学生在事实性知识和概念性知识的应用上已经熟练掌握,也都清楚解析几何解答题的变量最值问题的常用方法,但对于方法的选取以及数学运算等程序性知识和元认知知识的问题又显得无从下手.多数学生失分点集中在选取合适的变量与方法进行求解,将方程、函数、不等式进行转换,对应认知目标属于分析、评价过程出现问题.因此课堂教学的目标应聚焦于审清题目要求,以及为了解决问题如何引导学生整理思路,找到数学方法简化数学运算进而完成解答上.
通过以上问卷调查的数据分析,从低阶到高阶,学生的失分率越来越高,说明本题“卡脖子”的原因在于学生的高阶思维存在不足.
2 策略引导,变换技巧寻求突破
上题考查椭圆、抛物线的简单几何性质,直线与椭圆、抛物线的位置关系,线段的中点,这些知识点对高三学生来说都很熟悉,但大部分学生却做不出来,其原因在于缺乏对解决问题的路径进行规划,在变量的选取、方法的选择等问题上仍有欠缺,关键问题在于数学运算素养亟待提高.
数学运算是指在明晰运算对象的基础上,依据运算法则解决数学问题的素养.主要包括:理解运算对象,掌握运算法则,探究运算思路,选择运算方法,设计运算程序,求得运算结果.在解析几何问题中,运算素养主要体现在变量的选择、条件的代数解读、问题的代数解析.
常规做法很多时候不是最好的方法,在高考时间紧、难度大的背景下,若能对这一类题形成解题策略,学生便能提高得分率,更重要的是能引导学生从解题技巧的提高走向解题策略的提炼,成为以高阶目标驱动技巧方法、提升思维能力的教学.为了引出仿射变换,寻求椭圆与圆之间的联系,给出一道联考试题进行变式:
对以上变式,常规解题路径包括运用中点弦、联立方程用韦达定理、刻画三角形面积等,思路清晰计算量却巨大.引导学生思考:是否还有其他方法?
椭圆可以看成是圆保持横坐标不变、纵坐标压缩后得到的图形.圆有很多很好的性质,若能够得到椭圆与圆之间的变换关系(即压缩比),解题就会简化很多.解法如下:
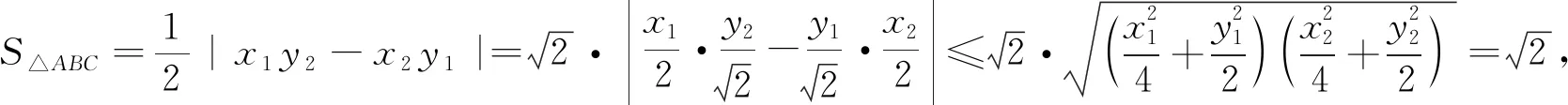
3 目标高阶,驱动性问题促进教学
一题多解在高中数学解题技巧中很常见,简化运算的本质是提高解题过程的思维含量,因此教师在教学过程中借助问题进阶将思维路径可视化显得尤为重要.
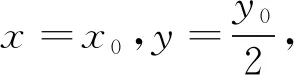
分析 课本上借助坐标关系求解轨迹方程的推理过程,旨在寻求点M与点P坐标之间的关系,以点P为中间量,得出点M横纵坐标之间的数量关系,这一过程揭示椭圆与圆的几何与代数关系,将学生不太熟悉的椭圆问题转化为圆的问题简化运算,将逻辑关系聚焦几何问题坐标化上,引导学生理解问题本质.
引导学生猜想:圆具有良好的几何性质,如垂径定理等,能否将椭圆变成圆,利用圆的有关性质来辅助解决椭圆的相关问题?
为了更好地剖析问题,引发学生深度思考,对照布鲁姆教学目标,设置以下几个思考问题,如表2所示.
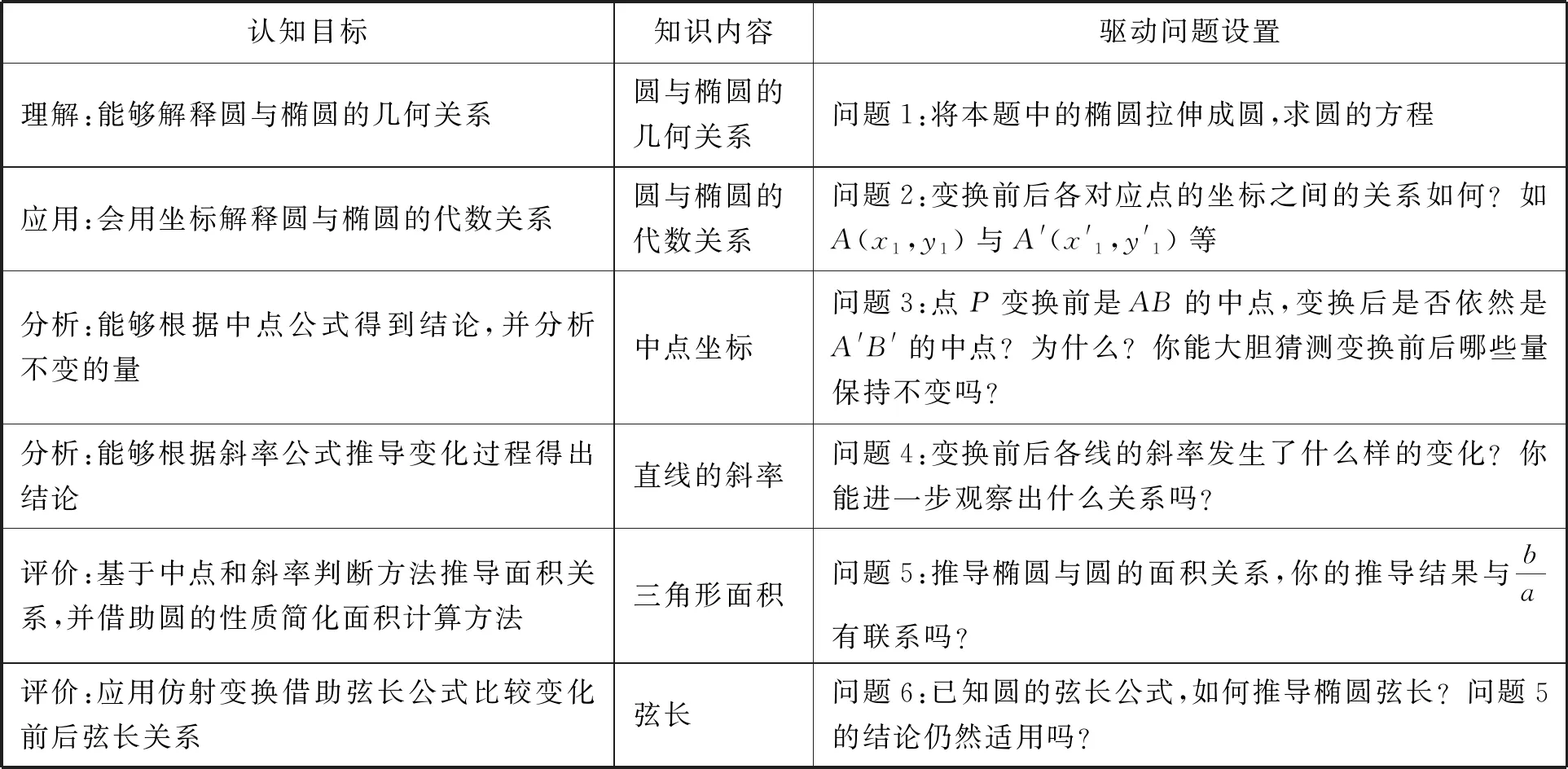
表2 认知目标与驱动性问题设置的对应关系