螺旋管内幂律流体流动传热优化模拟研究
2022-11-23王艳静陈为花包晓琳
张 浩, 张 志, 王艳静, 陈为花, 包晓琳
(1.山东建筑大学 热能工程学院, 山东 济南 250101; 2.山东省绿色建筑协同创新中心,山东 济南 250101; 3.山东英才学院 工学院, 山东 济南 250104; 4.山东省建筑设计研究院有限公司, 山东 济南 250001; 5.青岛腾远设计事务所有限公司, 山东 青岛 266100)
1 概述
螺旋管作为一种重要的工业管道[1],其特殊的结构使其传热效果远好于水平管,但相对于水平管的流动阻力更大[2]。因此,幂律流体在螺旋管中的流动传热优化研究相当重要。Guo等人[3]、陈群等人[4]在传统传热理论基础上,从多场协同角度综合考虑流动与传热,提出了强化传热场协同的基本概念。吕金升等人[5]在场协同原理下基于最小能耗散原理,建立不可压缩湍流模型,揭示了流体质点物理量间协同规律对强化传热和流动减阻的影响。黄云云等人[6]对圆形、椭圆形、矩形截面螺旋管内流动情况进行数值模拟,在湍流下获得温度场、速度场分布,探究流动过程温度场与速度场夹角对传热强化的影响。Pimenta等人[2]在实验过程中保持管道壁面温度一定,通过改变螺旋管半径、曲率、长度、螺距等,分析总结螺旋管内层流下牛顿流体与非牛顿流体对传热系数的影响。
目前,场协同原理用于螺旋管内幂率流体流动传热优化的研究鲜有报道。本文分别建立不同几何参数的螺旋管,采用模拟方法,对管内幂率流体流动传热进行场协同分析。为强化螺旋管内幂律流体流动传热,在螺旋管长度方向上分别增加矩形、三角形沟槽,分析沟槽形状、尺寸对改善管内流动传热的效果。
2 数学模型
2.1 几何模型
螺旋管三维几何模型见图1。螺旋管进口位于xOz面,原点O位于进口圆心,y轴垂直于进口截面。综合考虑螺旋直径、曲率等参数,设计了3种模型,尺寸参数见表1。
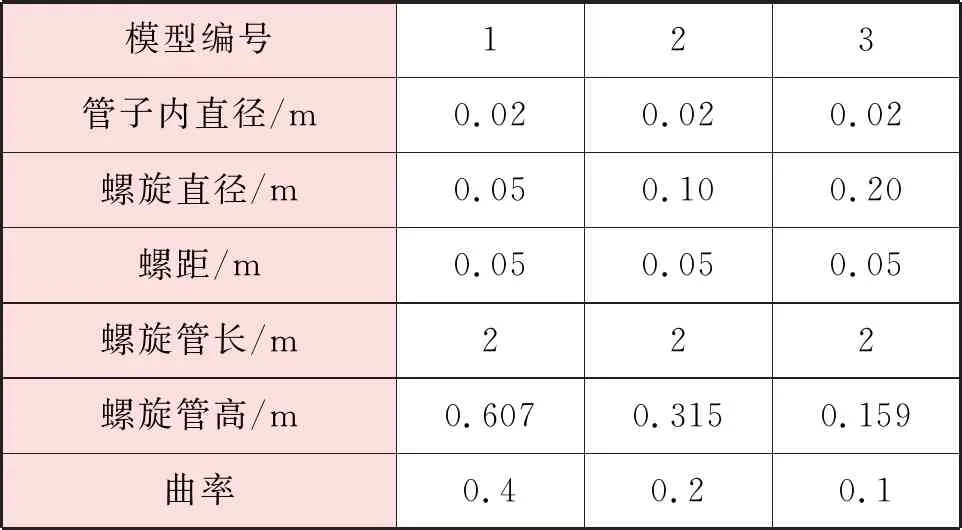
表1 3种模型尺寸参数

图1 螺旋管三维几何模型
螺旋管曲率κ的计算式为:
式中κ——螺旋管曲率
d1——管子内直径,m
d2——螺旋直径,m
2.2 控制方程
螺旋管内幂率流体的流动传热过程遵循流体流动的连续性方程、动量方程、能量守恒方程[7],螺旋管内湍流流动采用RNGk-ε模型[8]进行描述。湍流下,流体在近壁处的流动由黏性主导,在近壁处的传热采用增强壁面函数法描述。
幂率流体选用质量分数2%的羧甲基纤维素溶液(CMC溶液),稠度系数为3.58 Pa·sn,幂律指数n取0.5。比定压热容为4 200 J/(kg·K),密度为1 011 kg/m3。
2.3 边界条件
幂率流体进口温度设定为298.15 K,螺旋管壁面温度恒定为318.15 K。忽略模型进口效应,进口处为充分发展段[9]。幂率流体进口流速由设定雷诺数根据文献[10]提供的方法计算得到。出口相对压力为0,大气压力为101.325 kPa。
分别对层流、湍流进行模拟。层流、湍流下管子相对粗糙度选取0.000 075、0.033 300。
2.4 摩擦阻力系数求解方法
摩擦阻力系数f的计算式为:
式中f——摩擦阻力系数
Δp——幂率流体进出口压差,Pa
ρ——幂率流体密度,kg/m3
u——幂率流体进口流速,m/s
L——螺旋管长,m
根据尼古拉兹实验:层流时,摩擦阻力系数与管子相对粗糙度无关,仅与雷诺数有关。流体在过渡区时,摩擦阻力系数与管子相对粗糙度、雷诺数均有关。针对本文螺旋管模型,计算临界雷诺数得到[11]:当雷诺数为1 000~5 000时,为层流。当雷诺数为25 000~45 000时,为过渡区。
3 网格划分与模型验证
为保证计算精度和收敛速度,选用非结构化网格对几何模型进行网格划分[12]。以模型1为例,管子相对粗糙度0.000 5,雷诺数24 000~28 000,分别选取网格数17×104、37×104、58×104进行网格独立性验证。当网格数为17×104、37×104、58×104时,幂律流体出口温度分别为298.159、298.194、298.194 K。由此可知,从37×104开始,幂律流体出口温度基本不随网格数变化,因此网格数选为37×104。
为验证模型准确性,对水在相对粗糙度为0.000 075螺旋管内的湍流流动过程进行模拟。雷诺数变化范围为24 000~28 000,螺旋管壁面温度318.15 K,水进口温度为298.15 K。将摩擦阻力系数、努塞尔数模拟结果分别与采用文献[13]、[14]提出的关联式的计算结果进行比较。
摩擦阻力系数、努塞尔数模拟结果与关联式计算结果见图2。由图2可知,摩擦阻力系数模拟结果与关联式计算结果的相对误差小于5%,努塞尔数模拟结果与关联式计算结果的相对误差小于10%,且模拟结果与关联式计算结果变化趋势一致。说明模型具有一定准确性。

图2 摩擦阻力系数、努塞尔数模拟结果与关联式计算结果
4 流动传热优化分析
4.1 场协同分析
场协同理论综合考虑速度场与温度场,对二者协同程度对流动传热性能的影响进行评价。本文根据周俊杰等人[15]的分析,选用模点积平均角(为了评价整体区域速度场与温度场的协同程度,引入的全场平均协同角)作为螺旋管幂率流体流动传热场协同评价指标。为方便叙述,本文在名称上用场协同角代替模点积平均角。当场协同角为0°时,流动传热效果最好。当0°<场协同角<90°时,场协同角越小,流动传热性能越好;场协同角越大,流动传热性能越差。
管子相对粗糙度为0.000 075时,模型1~3场协同角随雷诺数变化见图3。由图3可知,管子相对粗糙度一定时,模型1~3场协同角均随雷诺数增大而增大。雷诺数一定时,场协同角随螺旋管曲率增大而减小。因此,曲率越大的螺旋管,温度场与速度场的协同程度越好,流动传热性能越好。
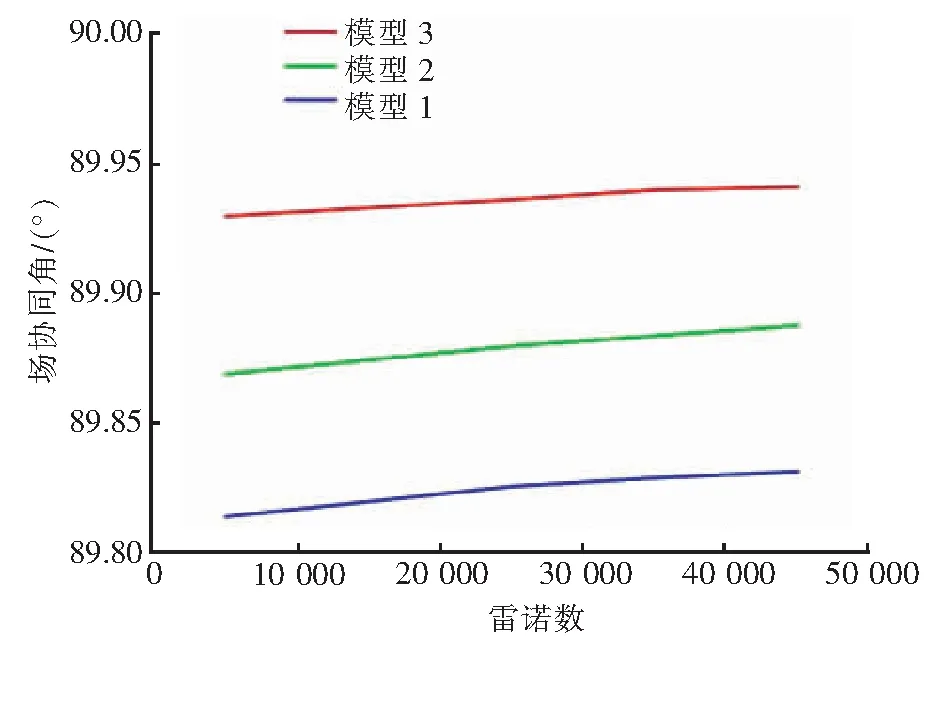
图3 管子相对粗糙度为0.000 075时3种模型场协同角随雷诺数变化
4.2 螺旋管结构优化
相对于直管,螺旋管可改变流体流动形态,减小边界层厚度,增强管内流体湍流强度,并有效促进管内物质混合。但螺旋管对流动传热的改善是有限的,为了强化螺旋管内幂律流体流动传热,在场协同原理指导下,对螺旋管结构进行优化。
选取模型3作为研究对象,在螺旋管长度方向上分别增加矩形、三角形沟槽,分析沟槽形状、尺寸对改善管内流动传热的效果。将增加沟槽后的模型分别命名为模型4~9,沟槽形状和尺寸见表2。增加沟槽后的螺旋管截面见图4。
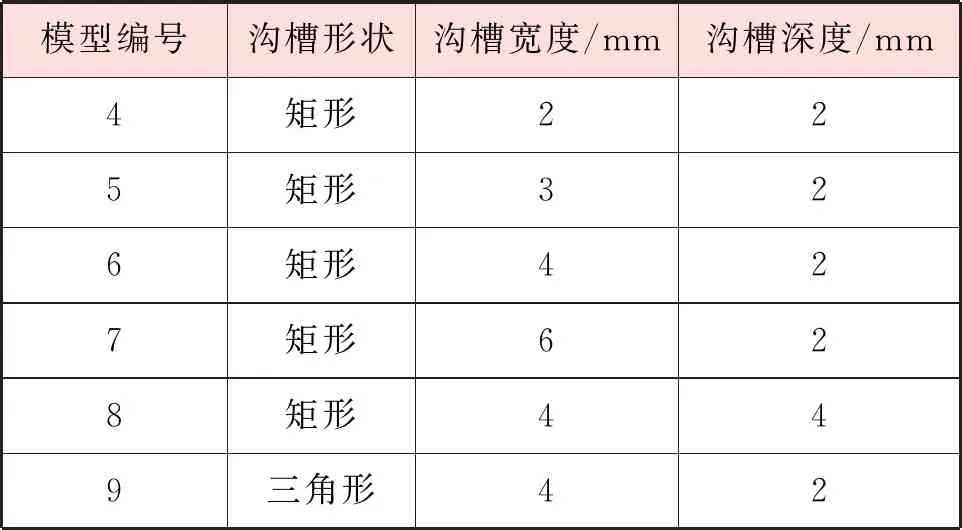
表2 模型4~9增加的沟槽形状和尺寸

图4 增加沟槽后的螺旋管截面
对模型4~9采用非结构化网格进行网格划分。以模型4为例,在管子相对粗糙度0.033 3、雷诺数35 000条件下分别选取网格数25×104、47×104、68×104进行网格独立性验证。由模拟结果可知,3种网格数对应的幂律流体出口温度分别为298.16、298.20、298.20 K。由此可知,网格数47×104、68×104对应的幂律流体出口温度相同,因此模型4网格数选取47×104。模型5~9的网格密度与模型4保持一致。
4.3 模型优化分析
① 摩擦阻力系数
管子相对粗糙度为0.000 075时,层流下模型3~9摩擦阻力系数随雷诺数的变化见图5。由图5可知,层流下,模型3~9摩擦阻力系数均随雷诺数增大而减小。与原型螺旋管相比,增加矩形、三角形沟槽后的螺旋管摩擦阻力系数增大,矩形沟槽的影响更加明显。对于增加矩形沟槽的螺旋管,当沟槽深度一定时,摩擦阻力系数随沟槽宽度增大而增大,沟槽深度的影响比宽度影响更大。
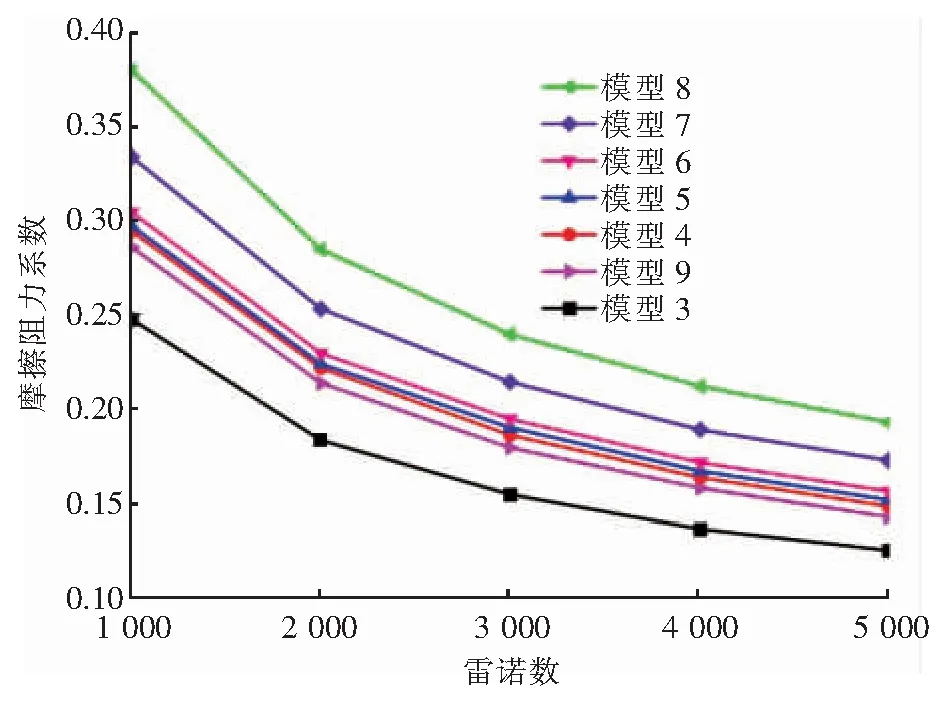
图5 管子相对粗糙度为0.000 075时层流下模型3~9摩擦阻力系数随雷诺数的变化
管子相对粗糙度为0.000 075、0.033 300时,湍流下模型3~9摩擦阻力系数随雷诺数的变化分别见图6、7。由图6可知,管子相对粗糙度为0.000 075时,湍流下模型3~9摩擦阻力系数的变化情况与层流基本一致,均随雷诺数增大而减小。由图7可知,管子相对粗糙度为0.033 300时,湍流下模型3~9摩擦阻力系数随雷诺数的变化情况与层流相反,均随雷诺数增大而增大。

图6 管子相对粗糙度为0.000 075时湍流下模型3~9摩擦阻力系数随雷诺数的变化

图7 管子相对粗糙度为0.033 300时湍流下模型3~9摩擦阻力系数随雷诺数的变化
② 努塞尔数
管子相对粗糙度为0.000 075时,层流下模型3~9努塞尔数随雷诺数的变化见图8。由图8可知,层流下,模型3~9努塞尔数均随雷诺数增大而增大。与原型螺旋管相比,增加矩形、三角形沟槽后的螺旋管努塞尔数增大,矩形沟槽的影响更加明显。对于增加矩形沟槽的螺旋管,当沟槽深度一定时,努塞尔数随沟槽宽度增大而增大,沟槽深度的影响比宽度影响更大。

图8 管子相对粗糙度为0.000 075时层流下模型3~9努塞尔数随雷诺数的变化
管子相对粗糙度为0.000 075、0.033 300时,湍流下模型3~9努塞尔数随雷诺数的变化分别见图9、10。由图8~10可知,与层流相比,湍流可增强流动传热强度。由图9、10可知,湍流下模型3~9努塞尔数均随雷诺数增大而增大。与管子相对粗糙度0.000 075相比,管子相对粗糙度为0.033 300时模型3~9努塞尔数更高。因此,增大管子相对粗糙度有助于增强流动传热强度。
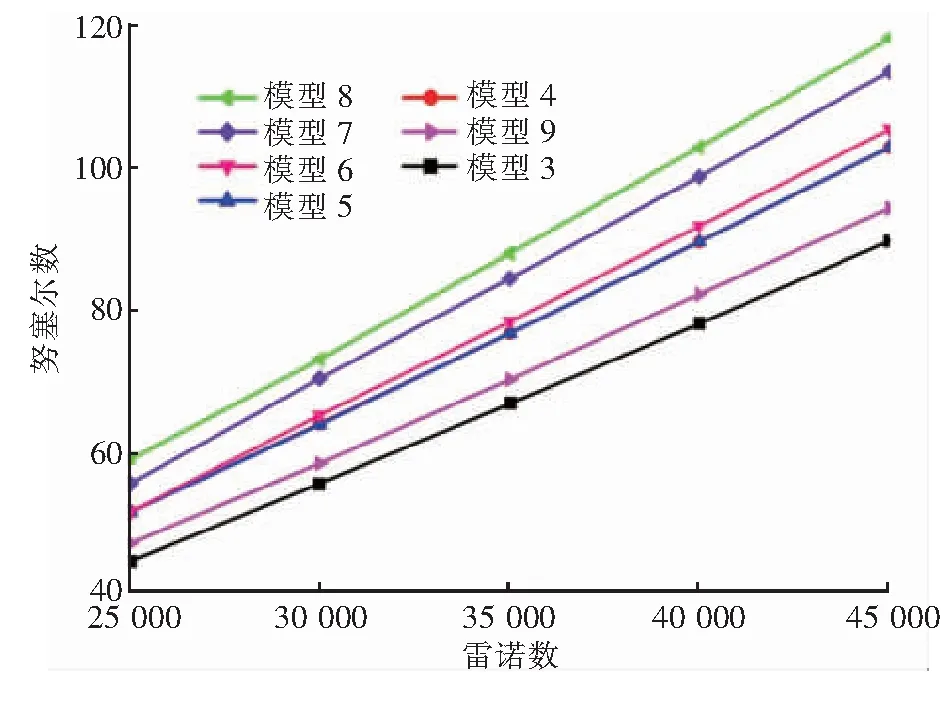
图9 管子相对粗糙度为0.000 075时湍流下模型3~9努塞尔数随雷诺数的变化

图10 管子相对粗糙度为0.033 300时湍流下模型3~9努塞尔数随雷诺数的变化
4.4 综合性能评价
传热强度得到加强的同时,一般易伴随流体阻力增大。为此,采用综合性能评价因子综合评价螺旋管的传热与阻力特性。综合性能评价因子φ的计算式为[16]:
式中φ——综合性能评价因子
Nui、Nuo——改进后、改进前螺旋管努塞尔数
λi、λo——改进后、改进前螺旋管摩擦阻力系数
综合性能评价因子同时考虑了摩擦阻力系数、努塞尔数。综合性能评价因子大于1,说明改进后螺旋管的综合性能得到加强,反之则说明综合性能降低[17]。综合性能评价因子越大,螺旋管综合性能越好。仍以模型3作为基准对象,改进前努塞尔数、摩擦阻力系数取模型3的努塞尔数、摩擦阻力系数。
管子相对粗糙度为0.033 300,模型4~9综合性能评价因子随雷诺数(1 000~45 000)的变化见图11。由图11可知,模型4~9综合性能评价因子均大于1,说明增加沟槽使螺旋管的综合性能得到加强。在模型4~9中,采用较大宽度、深度矩形沟槽的模型8的综合性能最佳,采用三角形沟槽的模型9的综合性能最差。
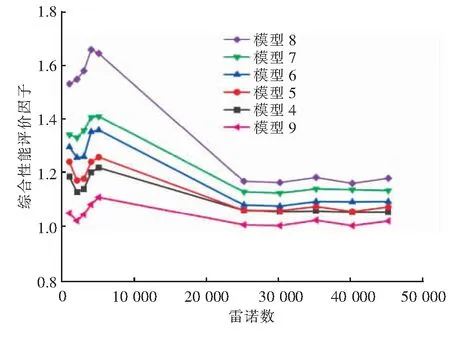
图11 管子相对粗糙度为0.033 300时模型4~9综合性能评价因子随雷诺数的变化
管子相对粗糙度为0.033 300、雷诺数为35 000,以模型7为例,模拟得到xOz截面场协同角云图(见图12)。由图12可知,进口段场协同角比较小,随幂律流体不断流动,场协同角逐渐增大直至稳定状态。管壁外侧的场协同角小于管壁内侧,说明管壁外侧的流动传热性能更好,宜针对管壁内侧适当采取强化传热措施,以提高换热效率。
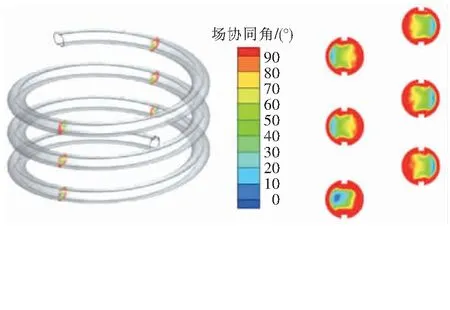
图12 模型7的xOz截面场协同角云图
5 结论
① 曲率越大的螺旋管,温度场与速度场的协同程度越好,流动传热性能越好。
② 与原型螺旋管相比,增加矩形、三角形沟槽后的螺旋管摩擦阻力系数、努塞尔数均增大,矩形沟槽的影响更加明显。对于增加矩形沟槽的螺旋管,当沟槽深度一定时,摩擦阻力系数、努塞尔数均随沟槽宽度增大而增大,沟槽深度的影响比宽度影响更大。
③ 与层流相比,湍流可增强流动传热强度,增大管子相对粗糙度有助于增强流动传热强度。
④ 增加沟槽使螺旋管的综合性能得到加强。采用较大宽度、深度矩形沟槽的螺旋管综合性能最佳,采用三角形沟槽的螺旋管综合性能最差。
⑤ 管壁外侧的场协同角小于管壁内侧,宜针对管壁内侧适当采取强化传热措施,以提高换热效率。
