海上核应急救援无人方舱稳性研究

李 铁 骊， 周 燹， 蒋 晓 宁， 林 焰*,2

( 1.大连理工大学 船舶工程学院, 辽宁 大连 116024；2.大连理工大学 工业装备结构分析国家重点实验室, 辽宁 大连 116024 )

0 引 言

随着海上经济和军事活动增多，诸多核电站、核动力舰船等事故被引发，救援难度大、核污染严重、人员无法靠近、固定维修设施易遭敌方打击等[1]，使得远海核应急快速响应及有效救援问题变得十分重要和迫切．无人艇相对于中大型救助船而言成本低、隐蔽机动性好、智能化程度高和快捷，可在较恶劣海况及在深远海域自主航行，避免人员伤亡[2-3]．因此将无人艇和核应急专用设备及装置有机结合，设计出适用于远海核应急救援的无人方舱，可适用于国产AG600救援飞机空投入水，具有在恶劣海况下自主航行抵达事故现场的能力，对海上核事故能做出快速响应，并进行检测、维修和补给．由于该方舱区别于常规船舶，尺寸小、自重轻，且搭载救援折叠吊臂等专用设备，因此在海上更容易发生失稳而倾覆，无法执行任务．因此，方舱外形设计要适合运载飞机的机舱空间要求，并采用流线形曲面[4]以减小航行阻力，提升快速性、耐波性、稳性及自扶正性能等[5]．在初步设计阶段，本文主要确定方舱主尺度及船型参数，研究静水力特性、稳性和自扶正性能，并绘制静水力曲线和稳性随重心高度zG变化图谱，基于自扶正需求确定极限zG，为后续设计、检验和性能研究等提供技术数据．

国内外学者对海上救援和无人艇稳性等方面展开了许多相关研究．文献[6]描述了东海舰队某基地装备部针对军舰应急保障需求研制出舰船装备机动保障的修理方舱组，其具有适应性强、集约性高、灵活机动性好等特点，但不适用于核应急救援．刘森林[7]开发了用于海上救援的无人艇，采用底部加载固定压块的方法满足自扶正性能，但降低了营救能力．Akyildiz等[8]从稳性角度综合分析了船型扶正法、充气袋法、活动压载法3种自扶正方法的优缺点，其中船型扶正法虽具有挑战性，但仍是最佳选择．方舱采用船型扶正法，可以节省布置空间、降低成本．Bai等[9]通过理论分析无人艇稳性随横摇变化情况，得知恢复时间对zG非常敏感；郑志江[10]通过分析中大型艇在静水和波浪中的自扶正能力，发现zG对其自扶正性能有很大影响，但都没有给出稳性随zG变化图谱．林志勇等[11]针对高速执法艇的自扶正能力需求，计算了不同参数对自扶正能力的影响，得知降低船舶重心是提高自扶正能力的主要措施．刘锦邦等[12]采用STAR CCM+对无人艇稳性进行仿真，并分析无人艇的自扶正性能随排水量和zG的变化情况，不过缺少对初稳性研究．

综上所述，无人艇应用于海上救援是一种创新，而且优势明显，但针对核应急救援方面研究尚少．为增强救援能力，方舱须具备优良的静水力特性、稳性及自扶正性能，其中zG是影响稳性的重要因素．因此，研究方舱在不同浮态下的静水力特性和稳性，确定自扶正要求的zG可行域对后续设备选型和总体设计有重要意义．本文先假定zG，研究稳性变化情况，以限定zG可行域．研究稳性主要与横倾后浮心位置有关，计算浮心位置与方舱静水力性能有关，而方舱主尺度及船型参数对静水力性能有重大影响，也是研究稳性的基础．所以首先确定方舱主尺度及船型参数；然后基于方舱静水力计算原理，采用等排水量计算法得到正浮、倒浮和向右横倾90°典型浮态下的静水力特性曲线，并分析其初稳性随吃水d和zG的变化情况；最后通过理论分析方舱稳性，得出自扶正计算流程，再计算满载工况和空载工况下，自扶正性能随zG变化情况，并对计算结果进行样条曲线拟合，得到满足自扶正性能的最大重心高度zGmax．

1 主尺度及船型参数确定

由于方舱单次运输能力越大越好且为保证救援能力，应满足自扶正等需求，因此采用单体全封闭形式以增加主尺度，并保证其总布置、浮性和稳性等要求．但这势必增加航行阻力，所以外形设计为流线形，以降低阻力，提高操纵性和稳定性等性能[13]．考虑到核应急快速响应需求，首选AG600救援飞机空投方舱，因此其主尺度和船型参数设计应考虑机舱空间的限制[14]，并达到最大载重能力．综合以上各方面需求，方舱主尺度及船型参数如表1所示，表中L为型长、B为型宽、D为型深、d1为满载吃水、d2为空载吃水、Δ1为满载排水量、Δ2为空载排水量、∇1为满载排水体积、∇2为空载排水体积、b1为满载时正浮浮心、b2为空载时正浮浮心、Cw为水线面系数、Cm为中横剖面系数、Cb为方形系数、Cp为棱形系数、Cvp为垂向棱形系数．为便于描述，建立如图1所示的坐标系Oxyz，设坐标系原点O是中线面、基平面和尾平面的交点，中线面和基平面交线为x轴，船首方向为正；尾平面和基平面交线为y轴，右舷方向为正；尾平面和中线面交线为z轴，向上为正．

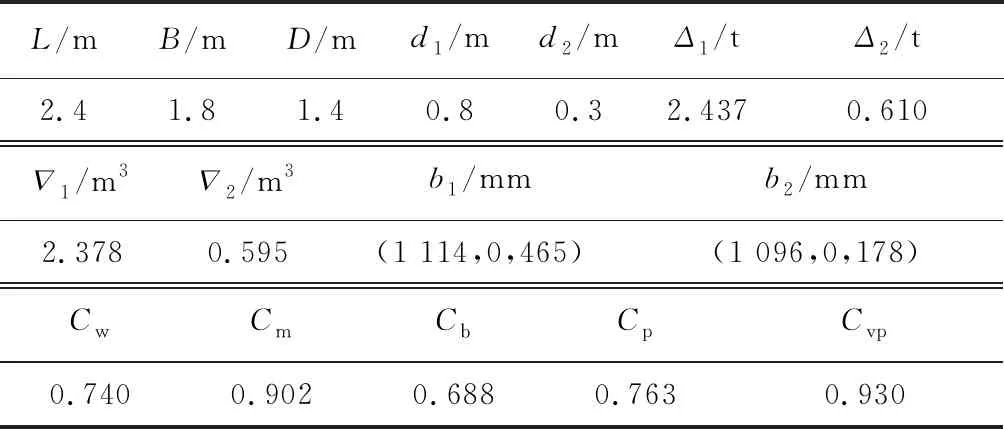
表1 方舱主尺度及船型参数

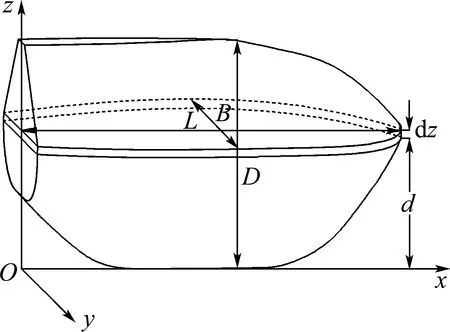
图1 方舱坐标系

2 方舱静水力特性研究

2.1 静水力计算原理

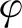
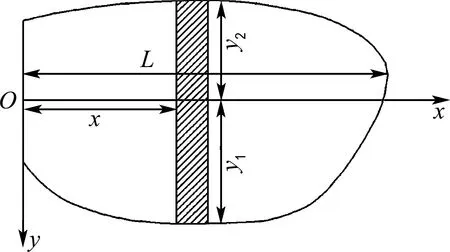
图2 横倾时水线面

(1)

(2)

(3)

式中：y1、y2分别为水线面左右半宽，MOy和MOx分别为Aw对x轴和y轴的静矩，f垂向坐标zf等于该横倾状态下的d；将Aw沿d方向进行积分便得到∇，即

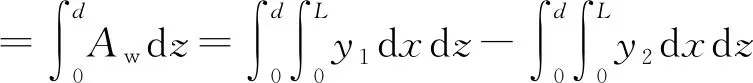
(4)

由∇乘以海水密度ρ可得到相应的Δ，计算∇对各个平面的静矩，进而得到Bφ坐标(xB，yB，zB)，即

(5)

(6)

(7)

式中：MyOz为∇对x轴的静矩，MxOz为∇对y轴的静矩，MxOy为∇对z轴的静矩．

方舱横倾时不再左右对称，不同d下Bφ可能不在同一铅垂线上，因此稳心M也不在同一铅垂线上，不过若只考虑M高度变化，仍可计算BφM和KM．下面假定某一d下任意横倾状态的方舱继续倾斜小角度φ时，Bφ移动曲线是以M为圆心、BφM为半径的圆弧，倾斜前后浮力作用线均通过M点．这样既使计算问题简化，又可较为准确地描述影响初稳性的各种因素．

如图3所示，等体积小角度横倾时，倾斜轴线通过f，出水、入水楔形体积都等于V，可认为倾斜后排水体积是由出水楔形W0OW1移至入水楔形L0OL1处，其形心自g2移至g1，方舱浮心由Bφ移动到Bφ，移动轨迹曲线的大小近似等于BφBφ，可知：

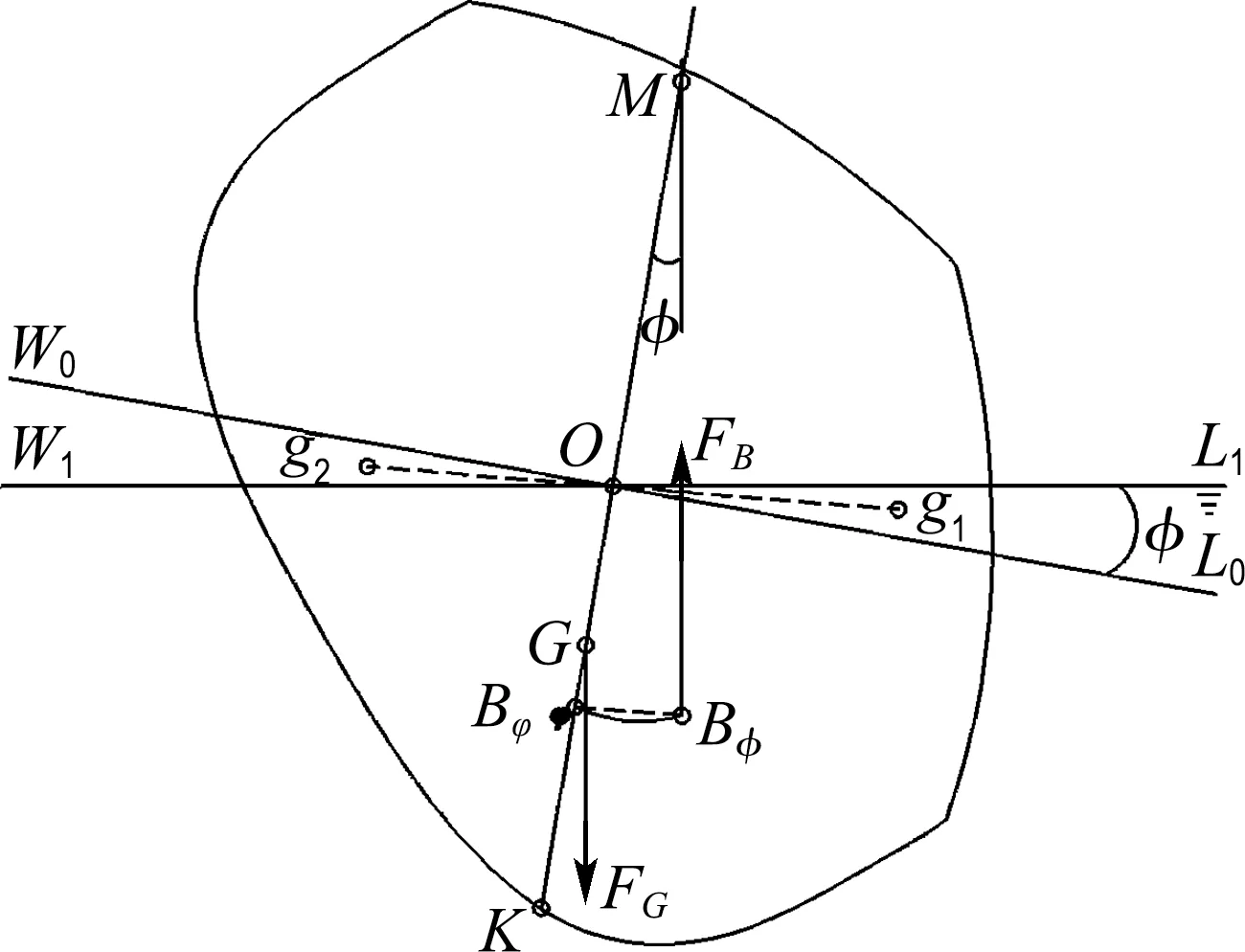
图3 稳心与稳心半径

(8)

式中：g1OV和g2OV是V对倾斜轴线O-O的静矩，其中入水楔形如图4所示，由图4可知：

图4 入水楔形

(9)

同理可得

(10)

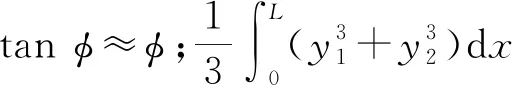
(11)

将式(11)代入式(8)得

BφM=It/∇

(12)

假定zG可得到GM，即

GM=KBφ+BφM-KG

(13)

式(13)中，KBφ=zB，KG=zG．基于静水力计算原理，可求得不同d下的Aw及其f坐标(xf，yf，zf)、∇及Bφ坐标(xB，yB，zB)、Δ、BφM和KM，并假定zG计算GM．为便于表述方舱浮态和初稳性随d的变化规律，将f坐标(xf，yf，zf)和Bφ坐标(xB，yB，zB)单位换算成mm，并根据计算结果绘制静水力曲线图和GM曲面图谱．

2.2 静水力曲线图和GM曲面图谱

方舱在不同作业工况和特殊浮态下，特别是其吊臂伸展作业时，可能使zG发生较大变化，甚至超出其主尺度范围，直至稳性失效而发生倾覆．为满足救援工况需求，初稳性要求方舱正浮时GM大于零，以保证抗倾斜能力，横倾和倒浮时GM都小于零，促使方舱倾斜而回到正浮状态．可根据KM计算结果，假定足够的zG，绘制GM曲面图谱，确定GM为零的临界线，由于GM=KM-KG，则此时zG与KM随d的变化规律相同，可将临界线投影到d-zG平面上，进而得到不同d下满足初稳性要求的zG可行域．为便于描述，分别采用相应坐标系对正浮、倒浮和向右横倾90°典型浮态进行静水力计算，并绘制静水力曲线图和GM曲面图谱，其计算流程如图5所示，最后将结论汇总在图1坐标系下．

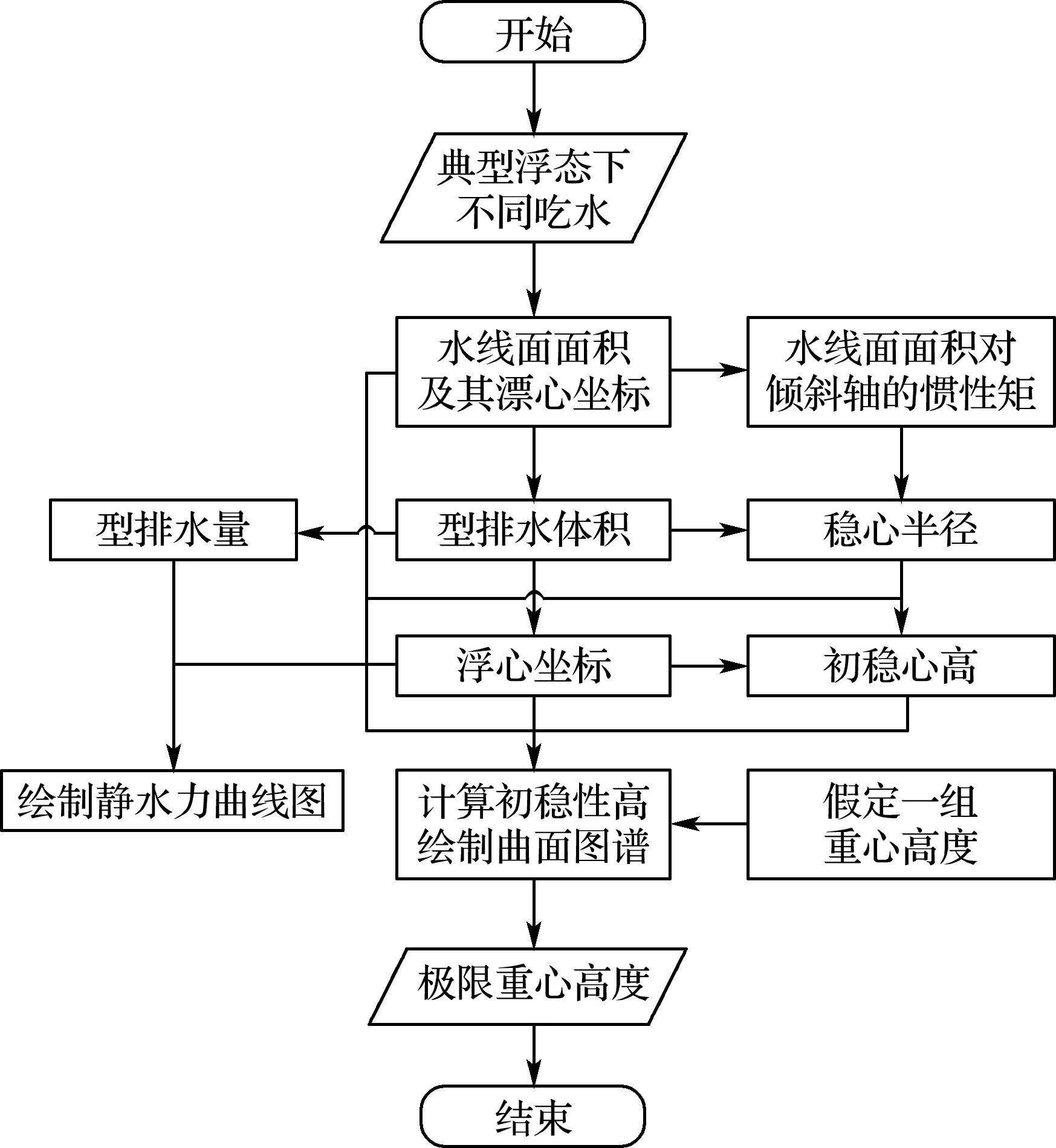
图5 静水力和初稳性高计算流程图

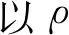
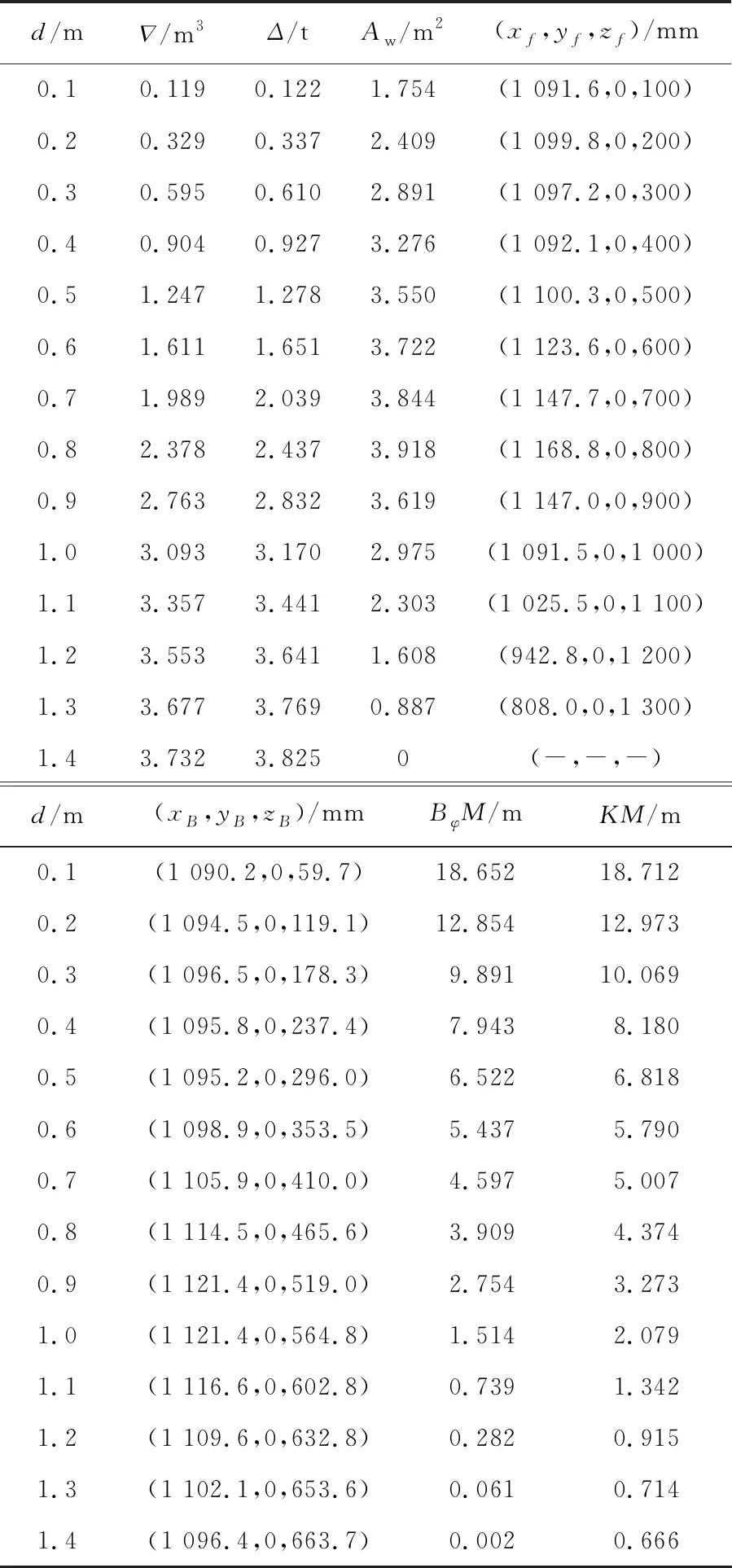
表2 正浮时静水力计算结果

基于上述结果绘制静水力曲线图，如图6所示，横坐标为归一化各量．

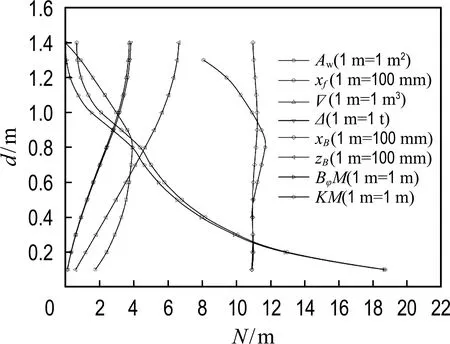
图6 正浮时静水力曲线图

根据KM计算结果，对于假定zG可以计算对应GM，并绘制在不同d和zG下的GM曲面图谱．如图7所示，GM随d和zG的增大而减小，当d=0.1 m，zG=0时，GM最大值为18.712 m；当d=0.8 m时出现拐点，曲线迅速下降．临界线上d=1.4 m时zG=666 mm，即d为0～1.4 m任意值时，zGmax为666 mm．在满载工况下，d=0.8 m，zGmax=4 374 mm；空载工况下，d=0.3 m，zGmax=10 069 mm．

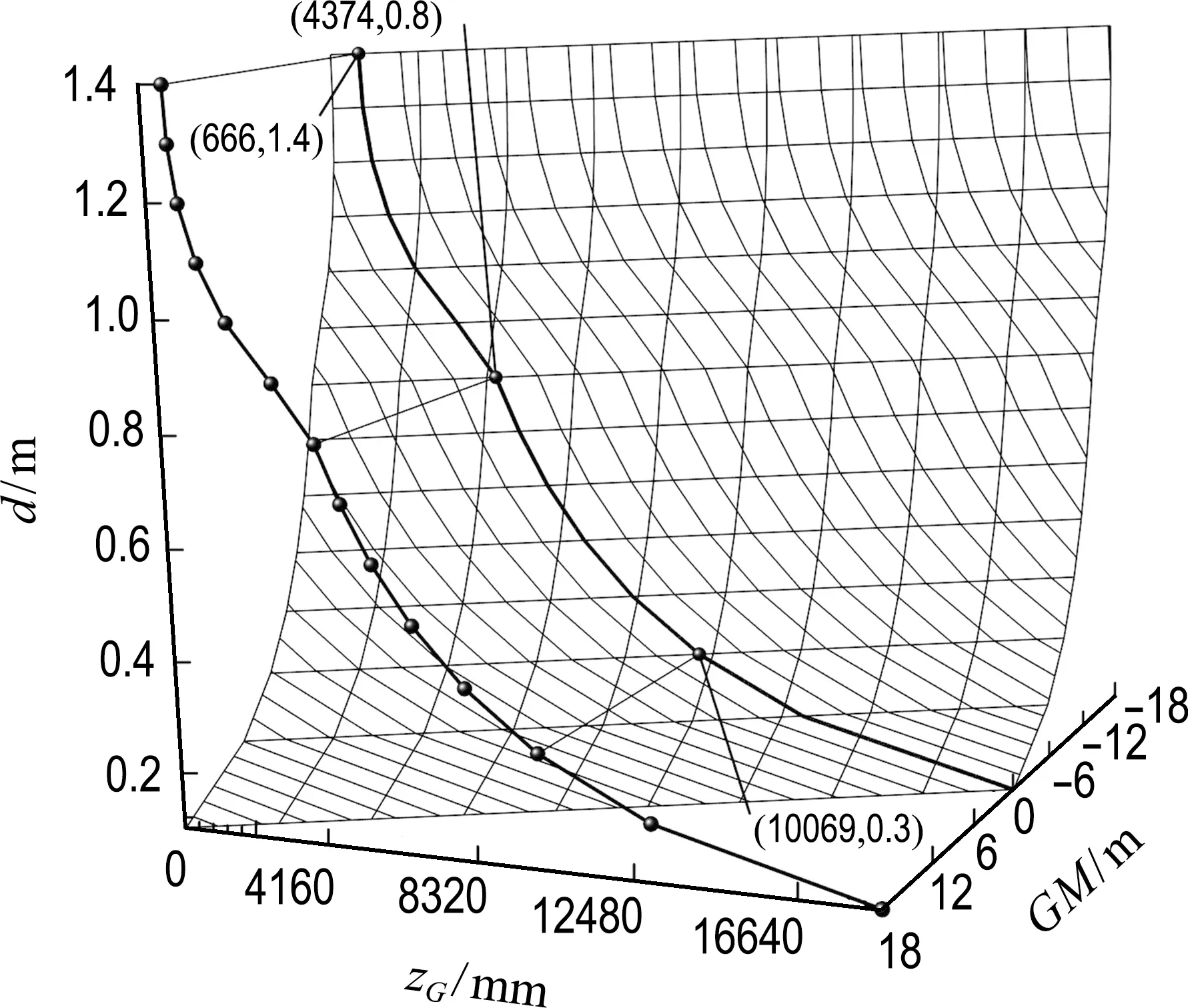
图7 正浮时GM曲面图谱

2.2.2 倒浮时静水力特性和初稳性图谱 方舱空投、航行或吊臂伸展作业时都有可能倾覆而产生倒浮状态，因此需计算倒浮时静水力特性和初稳性，其坐标系如图8所示．采用2.1中计算方法，可求得不同d下的Aw及其f坐标(xf，yf，zf)、∇及Bφ坐标(xB，yB，zB)和Δ，计算Aw对倾斜轴的惯性矩，可得BφM和KM，结果如表3所示．

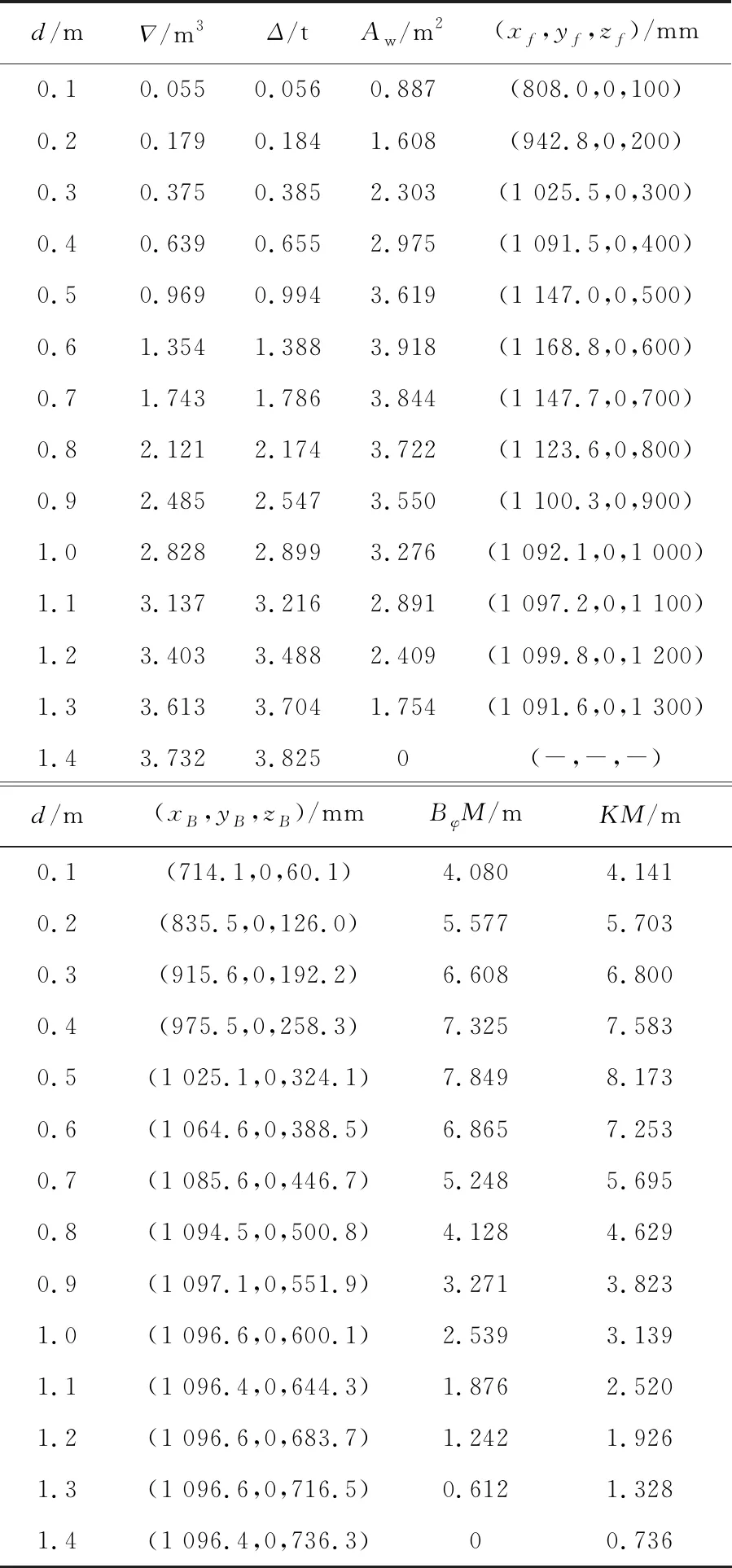
表3 倒浮时静水力计算结果

图8 倒浮时坐标系

由上述结果可绘制静水力曲线图，如图9所示．

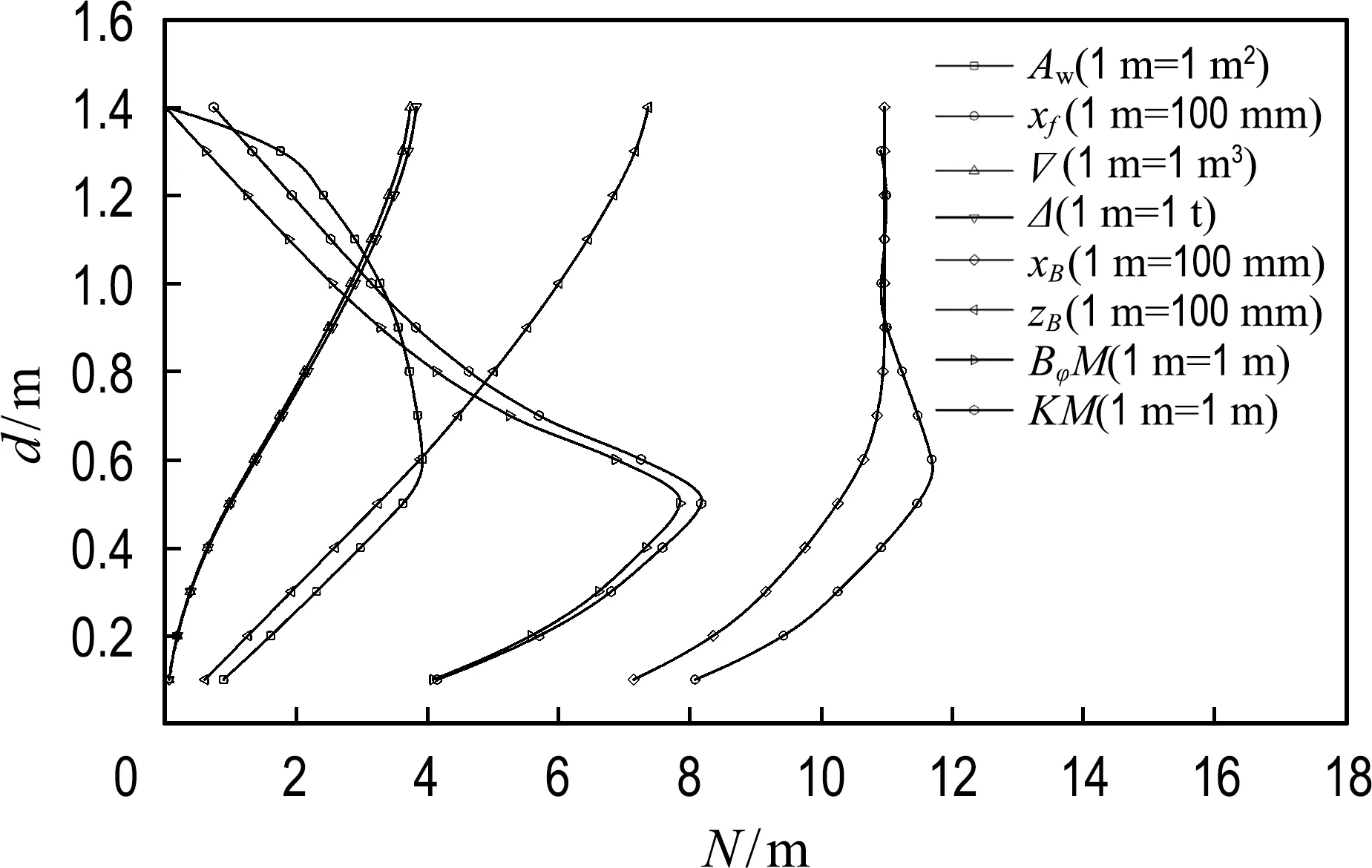
图9 倒浮时静水力曲线图

基于KM计算结果，可绘制GM曲面图谱，如图10所示．GM随zG增加而降低，但随d增加而先增加后降低，当d=0.5 m时(方舱上下壳体交线处，即正浮d1时)，GM出现峰值，在zG=0时，最大值为8 173 mm，当满足稳性要求的zGmin=8 173 mm时，GM=0，即图1坐标系下，d为0～1.4 m的任意值时倒浮，zGmax=-6 773 mm．临界线上d=1.4 m时，zGmin=736 mm，相当于图1坐标系下，zGmax=664 mm．由静水力曲线可知，方舱满载倒浮时，相同Δ下的d=0.871 m，zGmin=4 060.7 mm，相当于图1坐标系下的zGmax=-2 660.7 mm；空载倒浮时，d=0.383 m，zGmin=7 451.2 mm，即图1坐标系下zGmax=-6 051.2 mm．

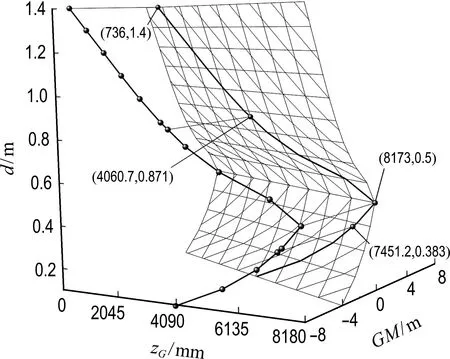
图10 倒浮时GM曲面图谱

2.2.3 横倾90°时静水力特性和初稳性图谱 方舱航行、作业或破损时会受力发生倾斜，不再关于x轴左右对称，下面只考虑M的高度变化，计算其静水力特性．以向右横倾90°典型浮态为例，坐标系如图11所示，采用2.1中计算方法可求得不同d下的Aw及其f坐标(xf，yf，zf)、∇、Δ及Bφ坐标(xB，yB，zB)、BφM和KM，结果如表4所示．

表4 横倾90°时静水力计算结果

图11 横倾90°时坐标系

由上述结果绘制静水力曲线图，如图12所示．

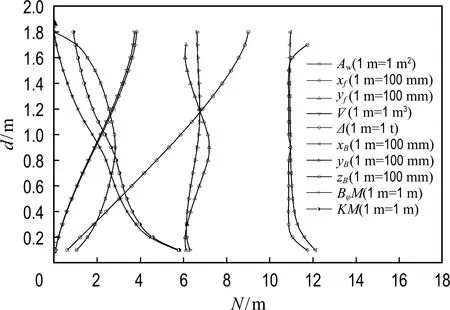
图12 横倾90°时静水力曲线图

同样根据KM计算结果，绘制GM曲面图谱，如图13所示．GM随着d和zG的增加而降低，在d=0.9 m(方舱中纵剖面)处出现拐点，zGmin=2 651 mm．d=0.1 m时GM最大值为5 805 mm，当zGmin=5 805 mm时，GM=0，即图1坐标系下，d为0～1.4 m任意值时右倾90°，满足稳性要求的yGmax=-4 905 mm．相应的d为0～1.4 m任意值时左倾90°，满足稳性要求的yGmin=4 905 mm．临界线上d=1.8 m时zG=900 mm，即向右横倾90°时，d=1.8 m处的zGmin=900 mm，同理左倾90°时，d=1.8 m处的zGmin=900 mm(图11坐标系下)，相当于图1坐标系下，d=1.4 m、yG=0时左右横倾90°初稳性都满足要求．满载右倾90°时，相同Δ对应的d=1.084 m，zGmin=2 102.9 mm，相当于图1坐标系下，yGmax=-1 202.9 mm，同理满载左倾90°时，yGmin=1 202.9 mm；空载右倾90°时，相同Δ对应的d=0.408 m，zGmin=3 607.9 mm，相当于图1坐标系下，yGmax=-2 707.9 mm，同理空载左倾90°时，yGmin=2 707.9 mm．

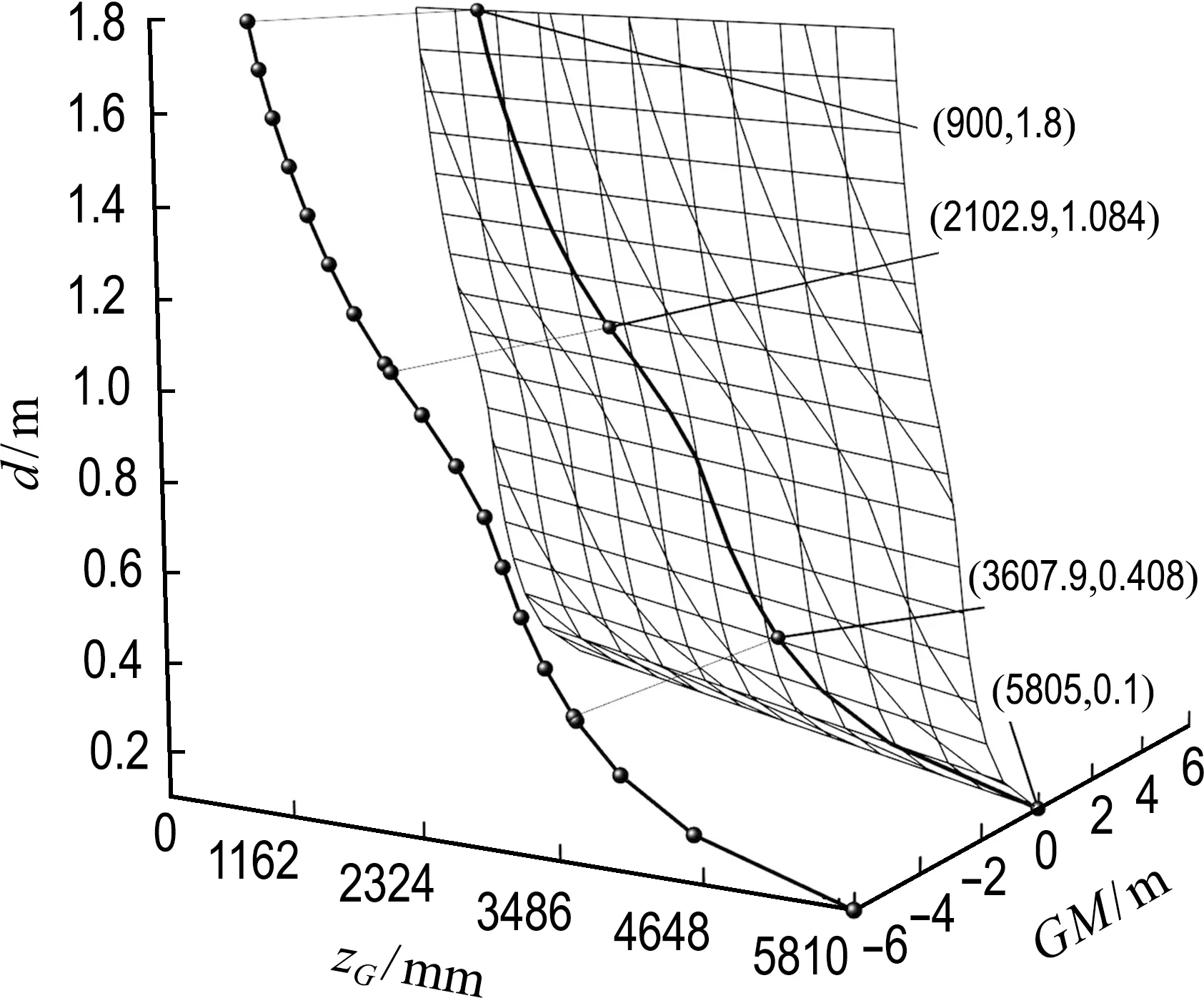
图13 横倾90°时GM曲面图谱

由结论可知yG越偏向外侧越容易倾斜，虽然满载、空载下横倾90°时yGmax和yGmin已经超出型宽范围，但实际情况更靠近船中，因为伸展吊臂时zG增大会促使方舱继续倾覆或者收回吊臂后zG减小促使其回正，两者都满足初稳性要求，不过设计时更倾向于zG偏小．

3 方舱自扶正特性研究

方舱稳性是指在受到外力作用下发生倾斜，当外力消失后仍能够依靠自身恢复到原平衡状态的能力[14]，而当横倾角为0°～180°内任意角度时，在外力消失后，都能够自行回到原平衡位置，则认为其具备自扶正性能[16]．通过概念分析可看出方舱自扶正问题是外力作用下的大倾角稳性问题，即在静稳性基础上进一步研究极限稳性，可采用大倾角稳性理论知识进行研究，并假定zG绘制静稳性曲线图谱，根据图谱判断其自扶正特性．

3.1 稳性计算原理

Mr=ΔGZ=Δl

(14)

Mr为正时可促使方舱恢复到原平衡位置，其中GZ是重心向浮心作用线作的垂线，垂足为Z，GZ大小可代表复原力臂l的数值大小[4]．由图14可知l计算式为

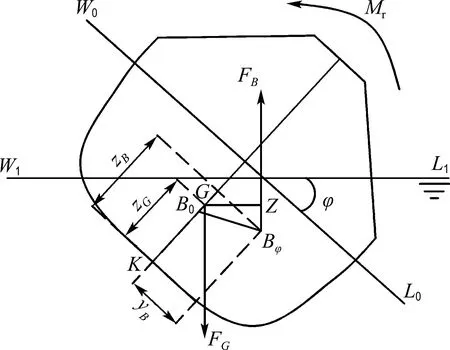
图14 复原力矩组成

(15)

3.2 自扶正性能计算流程

对于艇型确定的方舱，Bφ仅与d有关，按2.1 中的方法可求得Bφ坐标(xB，yB，zB)，当假定zG后，可计算l，进而验证其自扶正性能．首先基于2.1中的计算原理求得满载、空载工况下0°～180°的Bφ坐标(xB，yB，zB)，然后假定zG计算l并绘制静稳性曲线图谱，最后确定满足自扶正要求的zG可行域，并对zG和0°～180°横倾角下相应的lmin进行样条曲线拟合，以得到两种工况的zGmax．其计算流程如图15所示．

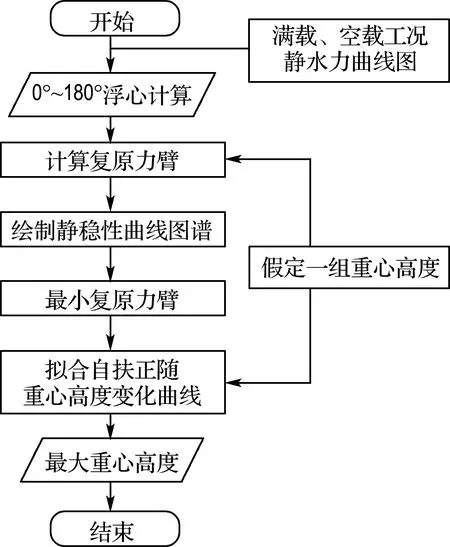
图15 自扶正性能计算流程图

3.3 自扶正性能分析

为研究方舱航行时的稳性及自扶正性能，分别绘制满载工况和空载工况下，l随zG变化的曲线图谱，并对lmin和zG采用Akima样条曲线插值拟合，以得到zGmax．其中样条曲线插值拟合是用低次多项式曲线作为每一小段区间的拟合曲线，该多项式曲线通过样本点且一、二阶导数连续，具有一定的光顺性，比较符合自扶正性能随zG的变化规律．

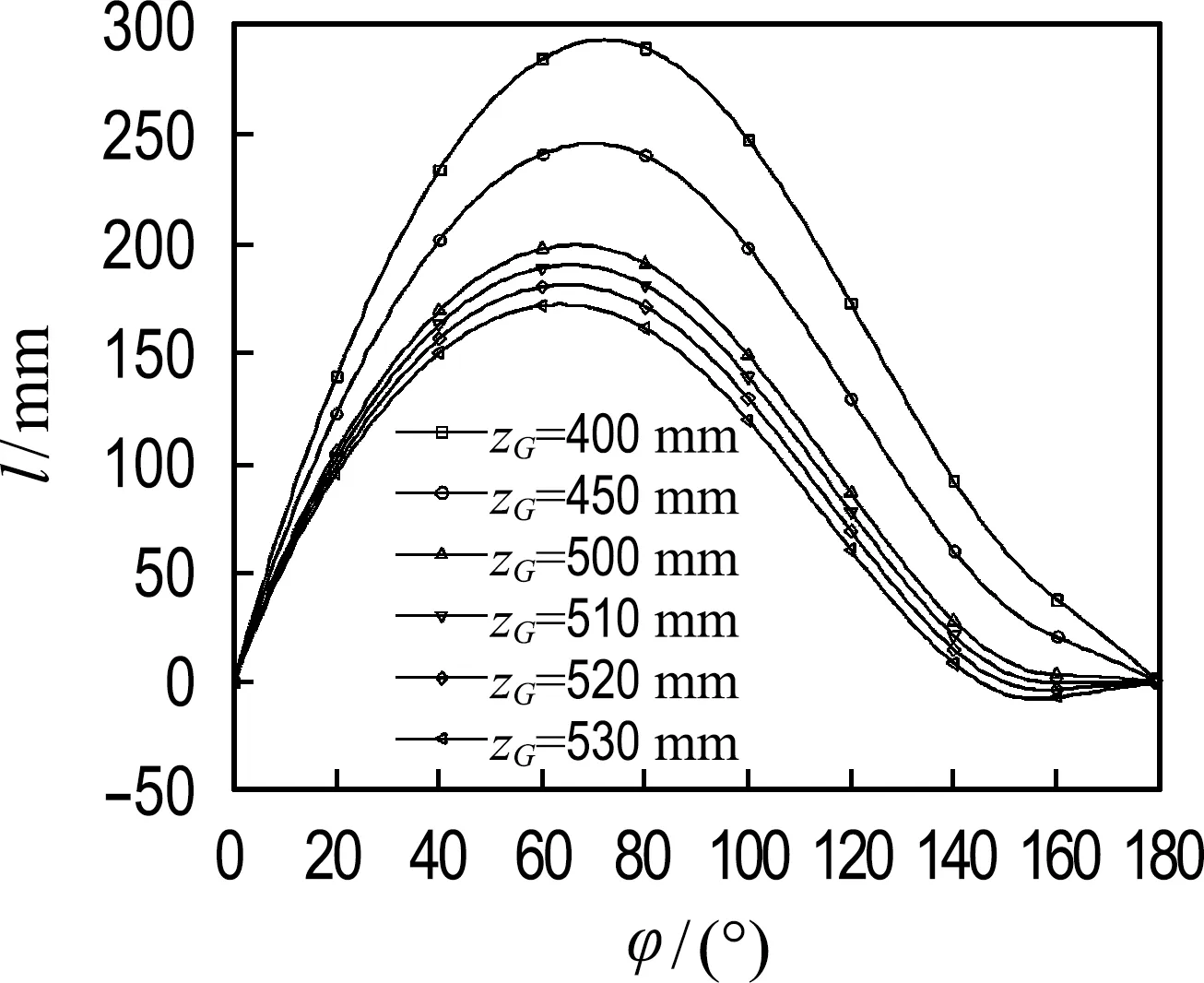
图16 满载工况下静稳性曲线图谱

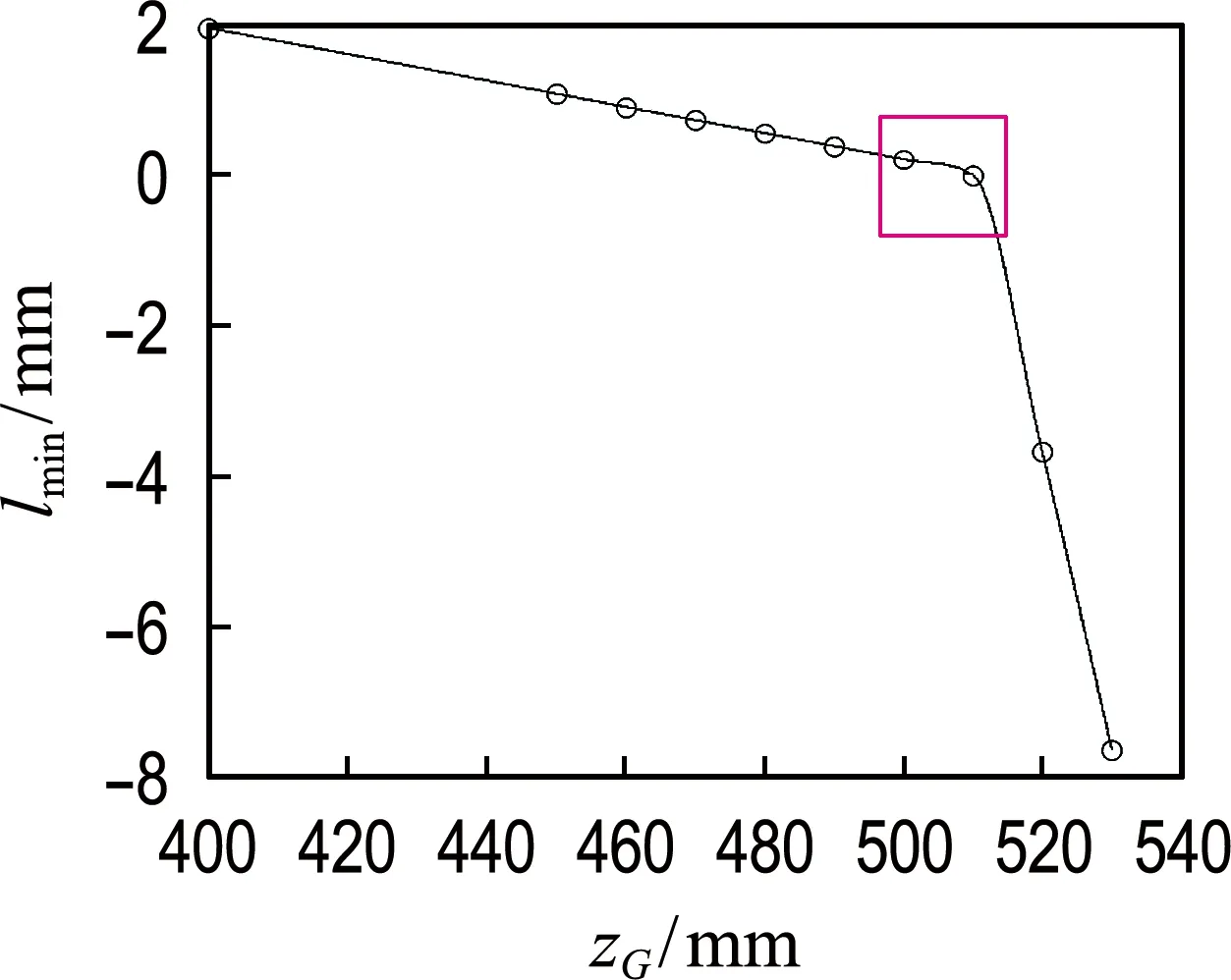
如图17所示，将lmin作为因变量，zG作为自变量，采用样条曲线拟合，可知zGmax=509.9 mm．

(a) 整体图

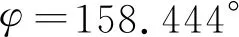
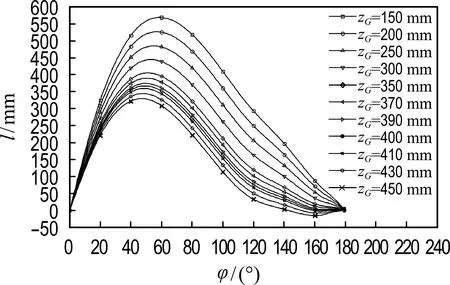
图18 空载工况下静稳性曲线图谱

如图19所示，将lmin作为因变量，zG作为自变量，采用样条曲线拟合，得到zGmax=401 mm．

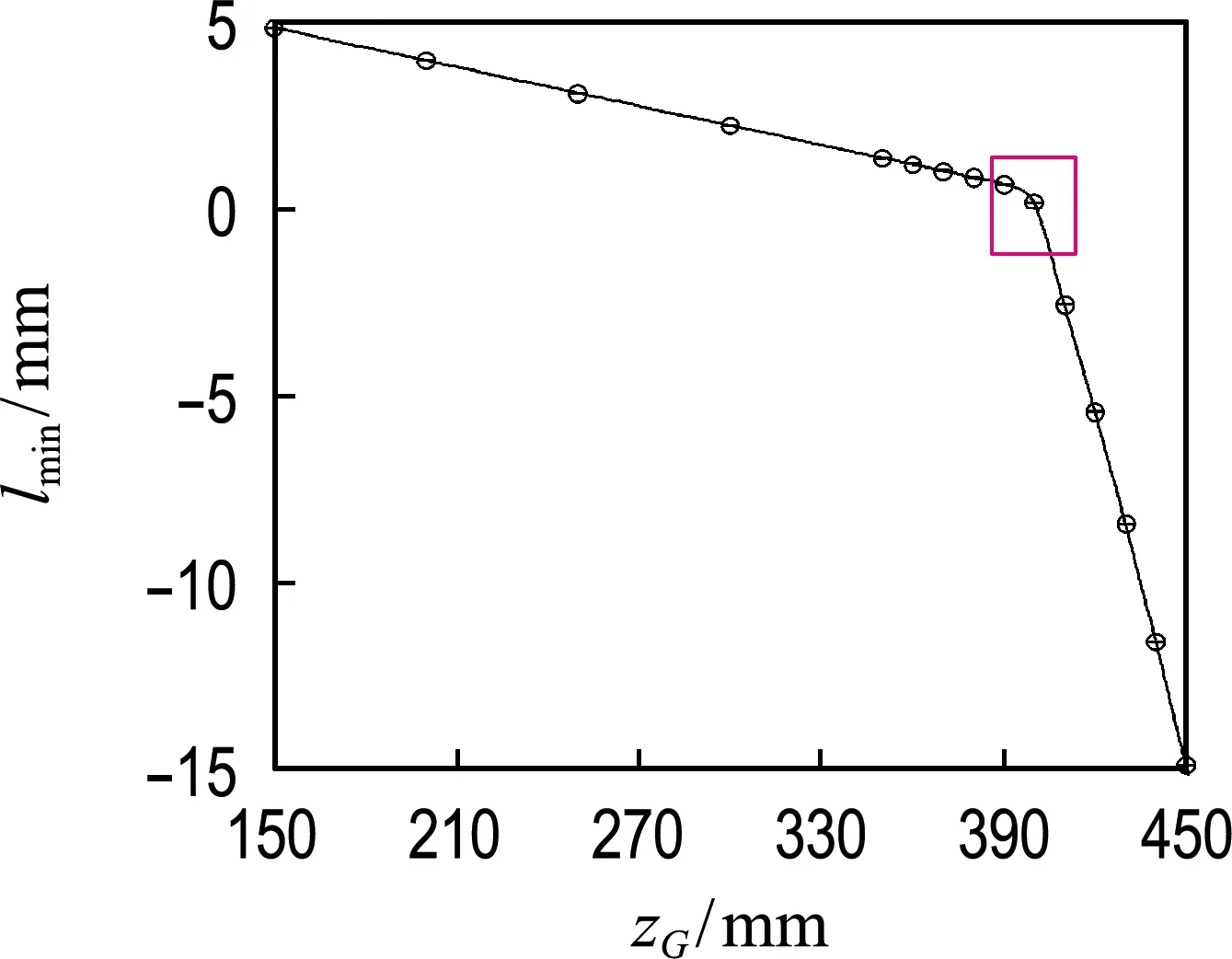
(a) 整体图

4 结 论

(1)本文设计的方舱适用于AG600飞机空投，考虑到机舱空间限制，并结合其总布置、最大载重量、稳性和快速性等需求，确定了主尺度及船型参数．

(2)基于等排水量计算法和初稳性计算原理，绘制了正浮、倒浮和向右横倾90°典型浮态下的静水力曲线图和GM曲面图谱，并得知GM随zG增大而减小，随d的变化规律与静水力曲线KM相同．在图1坐标系下，d为0～1.4 m的任意值时，满足初稳性要求的正浮zGmax=666 mm，倒浮zGmax=-6 773 mm，右倾90°时yGmax=-4 905 mm，左倾90°时yGmin=4 905 mm；满载工况下，正浮zGmax=4 374 mm，倒浮zGmax=-2 660.7 mm，右倾90°时yGmax=-1 202.9 mm，左倾90°时yGmin=1 202.9 mm；空载工况下，正浮zGmax=10 069 mm，倒浮zGmax=-6 051.2 mm，右倾90°时yGmax=-2 707.9 mm，左倾90°时yGmin=2 707.9 mm．

(3)根据静稳性曲线图谱，可知满载工况满足自扶正要求的zGmax取值范围在500～510 mm，采用样条曲线插值拟合得到zGmax为509.9 mm．空载工况满足自扶正要求的zGmax取值范围在400～410 mm，采用样条曲线插值拟合得zGmax=401 mm．因此其他工况满足自扶正要求的zGmax应在401～509.9 mm．

本文研究了方舱横倾状态下的静稳性，为研究其破损稳性和自由纵倾状态下的稳性及自扶正性能打下了基础，后续将进行模型试验和实际运营工况验证[18]．