不同应力路径下饱和重塑黄土的力学特性

2022-11-23赵丹旗付昱凯侯晓坤李同录

水文地质工程地质 2022年6期

赵丹旗，付昱凯，侯晓坤，李同录，李萍，李燕，张林

（1.长安大学地质工程与测绘学院, 陕西西安 710054；2.黄土高原水循环与地质环境教育部野外科学观测研究站, 甘肃正宁 745399；3.中国科学院地质与地球物理研究所, 北京 100029）

土体的力学特性不仅取决于土体本身性质，而且受到应力状态、应力路径等因素的影响，因此实际工程中要尽量选择可真实反映土体应力状态、加载方式、排水条件的应力路径进行试验[1-2]。

三轴试验可进行多种不同应力路径的试验，通常采用的是围压或平均主应力增大、减小或不变的路径，借此研究各类土体在不同应力路径下变形强度的差异[3-6]。早期学者对砂土进行试验研究发现了应力路径对土体应力-应变特性的影响，探讨了应力路径与本构模型的相关性[7-8]。江美英等[9]研究应力路径对饱和黄土孔隙水压力的影响，结果显示常规压缩、减围压压缩和等平均主应力路径下孔压差别较大，且轴向应变较小时孔压基本不受初始固结压力影响。许成顺等[10]试验发现了砂土在压缩条件下的剪胀性比拉伸条件下大，在减压压缩、常规压缩、增压压缩条件下的剪胀性依次减小，在压缩路径下的内摩擦角比拉伸条件下小。

以上应力路径可以模拟实际工程中的加载、卸载过程，而在边坡中常常遇到地下水位上升引起土体中应力路径变化的情况[11-12]。Brand[13]曾建议在室内试验中，通过增加孔隙水压力来模拟降雨引起的边坡破坏过程，即土体所受偏应力不变、平均有效应力减小的排水剪切路径。戴福初等[14]利用该路径分析了雨水入渗条件下剪缩型、剪胀型和临界状态型土的应力-应变特点与滑坡发生机理的关系。Chu 等[15]根据固结排水、固结不排水和常剪应力排水剪试验结果，提出了一种用修正状态参数和临界状态线描述砂土失稳条件的方法。赵春宏等[16]通过固结不排水和常剪应力排水剪试验，分析了填土滑坡的发生机理，结果显示该边坡是由于地下水位上升导致土体发生静态液化，从而形成了流滑。董全杨等[17]通过常剪应力排水剪试验验证了松散砂土在排水条件下会发生快速塑性变形。上述常剪应力排水剪试验在砂土中开展比较广泛，而黄土在该路径下的变形和强度特点仍需进一步研究。

我国黄土集中分布于陕西、甘肃、山西及宁夏地区[18]。这些地区的黄土不仅是一种自然沉积物，而且大量地作为土工材料，如地基、路基和建设场地等的填料。在这些填筑工程中，其含水率一般控制在最优含水率，底部设有排水设施。然而，随着时间推移，自然降水、绿化人工灌溉引起地表水下渗、周围高地向地下汇水或排水设施老化造成堵塞，会使地下水位不断上升，孔隙水压力增大，导致填土斜坡滑移，甚至挡墙破坏，将对正在运营的工程造成威胁。目前对这类由地下水位上升引起的滑坡机理研究多采用固结不排水试验，然而常剪应力路径能更好地描述该类滑坡。因此，本文制取饱和重塑黄土试样，使用GDS 三轴试验系统进行固结不排水（CU）和常剪应力排水剪（CSD）三轴试验，分析2 种路径下饱和重塑黄土的变形和强度特点，以便为实际工程选取合理的变形和强度指标提供参考。

1 研究方法

1.1 试样制备

试验土样取自陕西延安新城北区某一填土边坡，测得其比重为2.71，天然含水率为10.0%，液限为28.5%，塑限为18.7%，塑性指数为9.8，根据《土的工程分类标准》（GB/T 50145—2007），定名为低液限黏土[19]。用Bettersize 2000 激光粒度分布仪测得土样粒径分布曲线如图1 所示，可见黏粒（≤0.005 mm）质量占比为9.3%，粉粒（0.005～0.075 mm）为77.0%，砂粒（0.075～2 mm）为13.7%。黄土风干碾碎后过2 mm 筛，将筛下散土平铺于土工盘中，按照制样含水率10%计算加水量并将水均匀喷洒在土样上，用保鲜膜密封静置24 h 后充分拌匀，再置于保湿器中使土中水分布均匀。采用分层压制法制取干密度为1.40 g/cm3、直径50 mm×高100 mm 的圆柱试样，制样孔隙比为0.936。

图1 黄土试样粒径分布曲线Fig.1 Particle size distribution curve of the loess sample

1.2 试验方案

试验在GDS 三轴试验系统上完成。试验前采用常水头渗透和反压饱和相结合的方法对试样进行饱和，具体为：对试样施加20 kPa 围压和10 kPa 反压，打开试样与外界相通的排水阀门，在常水头下形成稳定渗流，并带出土体内气体；待水连续均匀流出排气完成后，关闭排水阀门；保持围压比反压大10 kPa，并以1 kPa/min 的速率同步增加围压和反压，最终围压增加至300 kPa 左右。孔压系数B（B=Δu/Δσc）通过增加围压测定孔压的方式获得，当B≥0.98 说明试样饱和。

饱和完成后，进行CU 或CSD 试验。CU 试验包括等压固结和剪切，具体为：饱和完成后，维持反压不变，并以恒定速率增加围压，使有效固结应力分别达到60，110，210 kPa，但实际值略有偏差。等压固结完成后，关闭试样与反压控制器的连接阀门，将加载方式由应力控制转换为应变控制，并按0.1 %/min 轴向应变速率进行剪切试验，试验结束的标准是轴向应变达到25%以上。

CSD 试验包括等压固结、偏压固结和常剪应力剪切。等压固结方法及有效固结应力设置同CU 试验。等压固结完成后，保持试样与反压控制器的连接阀门开启，对试样进行偏压固结，加载速率按0.01 %/min轴向应变控制。当偏应力q达到设定值时进入常剪应力剪切阶段，该阶段偏应力保持不变，以0.20 kPa/min的速率增加反压，直至试样破坏。具体试验方案如表1 所示。

表1 试验方案Table 1 Test schemes

2 试验结果分析

下面分析中，围压、轴向应变分别用σc、ɛa表示。平均应力p、平均有效应力p′、偏应力q的表达式如下：

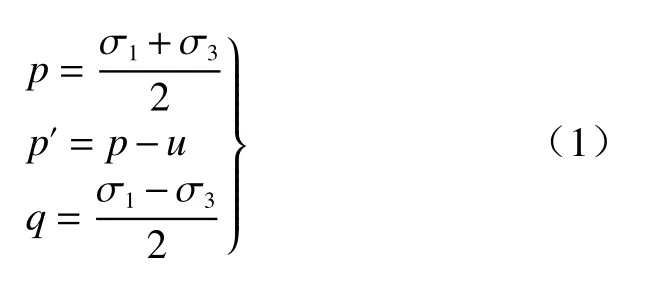
式中：σ1、σ3—最大、最小主应力/kPa；

u—孔隙水压力/kPa。

2.1 固结不排水路径下饱和重塑黄土的变形特点

图2 为CU 应力路径的试验结果。首先为等压排水固结阶段，偏应力为0，应力路径自原点沿p轴右移。然后进入应变控制不排水剪切阶段，总应力路径沿45°线上升到峰值偏应力，再原路返回到残余偏应力；有效应力路径随孔隙水压力不断增大而偏离总应力路径，在偏应力上升的同时，平均有效应力小幅增大后减小，偏应力达到峰值后开始下降，最后沿着破坏线继续下降。

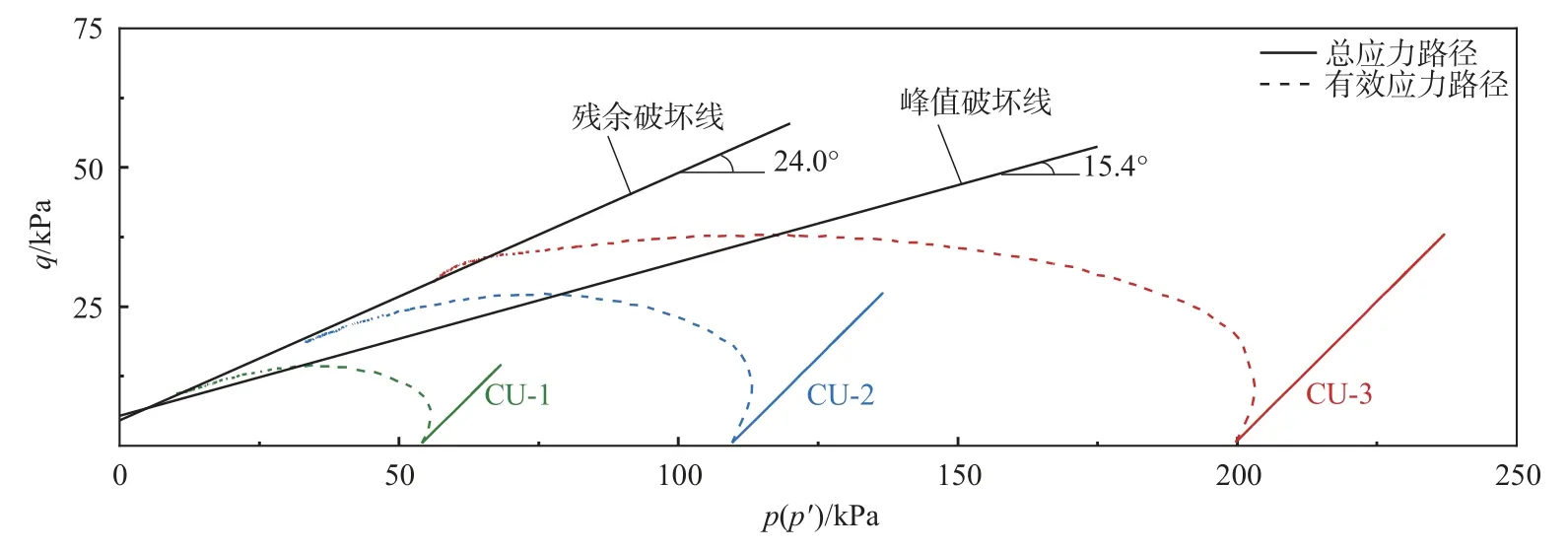
图2 CU 试验应力路径Fig.2 Stress path of the consolidated undrained tests

图3 中实线为不同围压下的应力-轴应变曲线。在3 种围压下，曲线均呈弱软化型，即偏应力达到峰值后有小幅度下降。以偏应力峰值为界，将曲线划分为2 个阶段。第1 阶段，偏应力随轴向应变的增大而陡升，围压越大增速越快，当轴向应变达到1%左右，偏应力达到峰值。第2 阶段，偏应力随轴向应变的增大而缓慢下降，当轴向应变达到15%时，偏应力趋于稳定，土体达到残余状态。偏应力峰值对应的应力状态点为峰值破坏点，轴向应变25%时对应的应力状态点为残余破坏点，用直线拟合即可得到峰值破坏线和残余破坏线[20-21]。

图3 应力q、孔压u 与轴应变ɛa 关系曲线Fig.3 Curves of q-ɛa and u-ɛa

图3 中虚线为孔隙水压力随轴应变的变化曲线。可以看出，围压越大，初始孔压随轴向应变的增速越快，最终稳定值也越高。在偏应力达到峰值前孔压呈非线性快速增长，孔压增速减缓时，偏应力开始减小。当应变为5%时，孔压趋于稳定。CU-1、CU-2、CU-3的孔压终值分别约为围压的98.1%、86.9%、86.5%，也就是低围压下，孔压几乎接近围压。孔压上升是土样应变软化的原因，也表明土体在剪切阶段发生了剪缩。试样最终呈中部鼓胀破坏，如图4（a）所示。

图4 2 种应力路径下土样都呈现鼓胀破坏Fig.4 Swelling failure of the soil samples under both stress paths

2.2 常剪应力路径下饱和重塑黄土的变形特点

图5 中实线为CSD 试验的应力路径，虚线为轴应变随平均有效应力的变化曲线，图6 为孔隙水压力随轴应变的变化曲线。3 种围压下的试验曲线形态一致，故以CSD-3 为例进行分析。

图5 CSD 试验应力路径与轴应变-平均有效应力曲线Fig.5 Stress path of the constant shear drained tests and ɛa-p′ curves

图6 孔压-轴应变曲线Fig.6 Curves of u-ɛa

O—A3和A3—B3段分别为等压和偏压固结阶段，都在排水条件下进行，孔压接近0。应力路径先沿p轴右移，再沿45°线到目标应力点。这2 个阶段产生少量轴向变形，围压越大变形越多。

B3—D3段为常剪应力剪切阶段，维持偏应力不变，通过施加反压使平均有效应力减小，应力路径水平左移达到破坏线。为ɛa-p′曲线开始出现上升趋势的临界点，以此为界将常剪应力剪切阶段分为2 段。B3—C3段，随着孔压增大，试样仍处于稳定状态，几乎没有产生轴向变形。C3—D3段，轴向变形加速发展，试验过程中可观察到试样中部开始鼓胀。CSD-1、CSD-2、CSD-3 在Di（i=1,2,3）点的应变分别为10.3%、15.4%、16.4%。3 种围压下Ci、Di点的孔隙水压力情况列于表2。

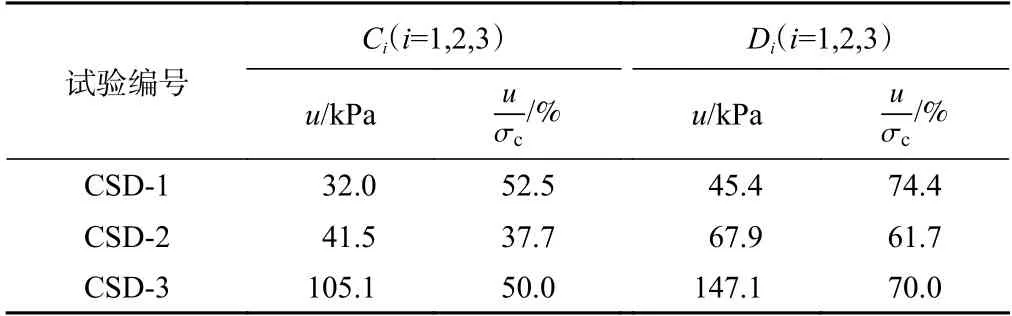
表2 Ci、Di 点的孔隙水压力Table 2 Pore water pressure at Ci and Di

D3—E3段为破坏阶段，偏应力不能维持常数，而是沿破坏线下降。该阶段轴向变形失控，突然增长，试样快速鼓胀破坏，如图4（b）所示。

由于常剪应力剪切阶段偏应力为常数，因此这里取ɛa-p′曲线开始出现上升趋势的临界点对应的平均有效应力点Ci为等效峰值破坏点，其拟合直线即为CSD 路径的等效峰值破坏线。另外，取偏应力失稳下降点Di为残余破坏点，从而确定残余破坏线的位置。

2.3 2 种应力路径下饱和重塑黄土的强度

图2 和图5 在p-q坐标上分别绘制了2 种应力路径下的峰值和残余破坏线。将这2 组强度破坏线放在同一个图上比较，如图7 所示。再利用p-q坐标下破坏线的倾角α和截距a，由式（2）求得相应的有效内摩擦角和有效黏聚力，计算参数和计算结果汇总于表3。

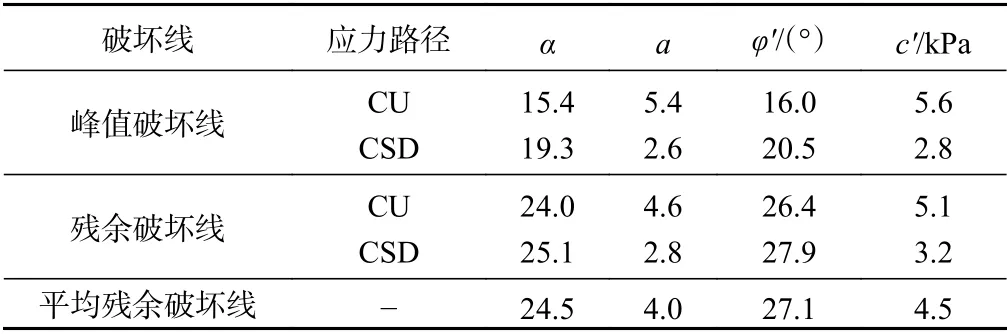
表3 2 种应力路径下饱和重塑黄土的有效抗剪强度指标Table 3 Effective shear strength indexes of the saturated remolded loess under two stress paths

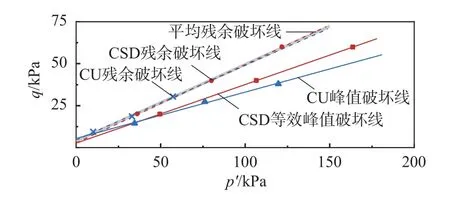
图7 2 种应力路径的破坏线Fig.7 Failure lines of two stress paths

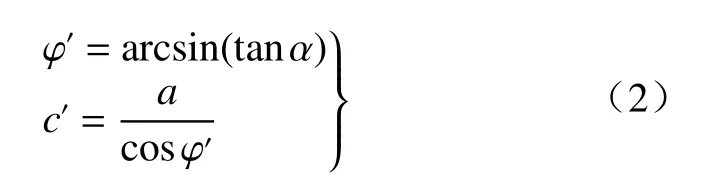
式中：α—破坏线与p′轴的夹角/（°）；

a—破坏线在q轴上的截距；

φ′—有效内摩擦角/（°）；

c′—有效黏聚力/kPa。

由图7 可见，CSD 与CU 路径下，峰值破坏线的位置相差较大，而残余破坏线的位置相差较小，也就是说应力路径对有效峰值强度的影响比较大。换算为有效内摩擦角和有效黏聚力，可见在CSD 路径下的峰值内摩擦角比CU 路径下大4.5°，残余内摩擦角比CU 路径下大1.5°，峰值黏聚力、残余黏聚力比CU 路径下小2.8 kPa、1.9 kPa。2 种路径下土体有效残余强度指标的差异是缘于在各自独立的坐标下计算出来的。由图7 可以看出，2 种路径下的残余值散点几乎分布在1 条直线上。将2 种路径下的残余破坏点按1 条直线统计，可得其平均倾角和平均截距，再由式（2）换算为φ′和c′，分别为27.1°和4.5 kPa，其值一并列于表3 中。2 种应力路径下的有效残余强度很接近，说明有效残余强度是重塑黄土的内在属性，不受外在应力边界条件的影响。