考虑预报偏差的迭代式集合卡尔曼滤波在地下水水流数据同化中的应用

杨 运，吴吉春，骆乾坤，钱家忠

（1.南京大学地球科学与工程学院水科学系，江苏 南京 210023；2.水利部淮河水利委员会，安徽 蚌埠 233001；3.合肥工业大学资源与环境工程学院，安徽 合肥 230009）

集合卡尔曼滤波（Ensemble Kalman Filter，EnKF）是一种顺序数据同化方法，可以融合多源观测信息实现系统状态动态更新[1-6]。其在大气科学[7]、海洋科学[8]、石油工程[9]等诸多领域得到了广泛的应用。在水文地质领域，研究者通过同化水位数据[10]、浓度数据[11]、地球物理数据[12]等观测资料，开展了水文地质参数反演、地下水污染源识别、地下水水流和污染物运移预测等研究。同时，为使EnKF 方法适应强非线性、非高斯问题，一些学者对其进行了改进。南统超等[13]引入局域化修正方法，减小了小集合样本抽样带来的伪相关的影响。张秋汝等[14]提出一种改进的全局迭代集合卡尔曼滤波方法，并通过非饱和土壤水数据同化问题研究了不同迭代式方法在降低参数和变量不一致性上的性能。周海燕[15]提出正态转换—集合卡尔曼滤波方法，在正态分布空间里进行同化更新，成功用于非高斯含水层参数识别，并进一步用于识别非高斯含水层中地下水污染源[16]。

预报模型是集合卡尔曼滤波方法的重要组成部分，以往研究多建立在预报模型准确的基础上（即预报模型不存在错误或预报模型仅存在服从零均值高斯分布的白噪声）。许多实际问题如地下水水流数据同化，由于野外水文地质条件复杂及认知的局限性，地下水水流模型结构很难准确刻画，模型概化存在不确定性，而模型概化不准确必将导致预报偏差[17-20]。研究表明忽视这种偏差会造成数据同化效果不佳，带来错误的系统估计或低估系统的不确定性[21]。针对模型概化存在不确定性的数据同化问题，目前处理方式主要有2 种：（1）基于贝叶斯模型平均理论，采用几种备选预报模型分别进行数据同化，再对同化结果进行模型平均从而降低单个备选模型预报偏差的影响。如Xue 等[22]将EnKF 集合到模型平均框架中，应用于地下水水流模型边界水头大小和渗透系数场变异函数模型不确定条件下的数据同化。实际问题中很难判断备选模型是否已涵盖所有合理的模型结构[23]，因此采用这种方式存在一定局限性。（2）给预报模型增加一个偏差项，偏差项也利用观测数据同步更新，获得的预报模型认为是无偏的模型参与数据同化。Kollat等[24]用这种方式求解了砂箱实验中地下水污染物泄露过程不确定情况下的污染物运移预测问题，研究表明基于偏差的EnKF 方法能够预报得到接近于真实情况的浓度穿透曲线。Erdal 等[21]研究了非饱和带土壤分层结构不确定条件下的水分运移问题，基于偏差的EnKF 方法显著优于未考虑偏差的数据同化结果。然而，在基于偏差的EnKF 方法的应用中，对于引入偏差项可能增大参数和变量不一致性的问题并未进行深入分析，且其适用性也需进一步研究。

因此，本文提出考虑预报偏差的迭代式集合卡尔曼滤波（Biasaware Ensemble Kalman Filter with Confirming Option，Bias-CEnKF）方法，并将其应用于地下水水流模型中边界条件、初始条件、源汇项等分别存在概化不准确的情形时非均质含水层渗透系数场识别和地下水水流预测问题。

1 研究方法

1.1 标准集合卡尔曼滤波（EnKF）

标准EnKF 通过模型预测和同化更新2 个步骤实现数据的顺序同化。主要过程为：

（1）定义tk时刻增广状态矩阵Sk，包括状态变量矩阵mk、模型参数矩阵θk，即：

（2）对tk时刻状态变量进行预测得到mfk：

式中：F—预报算子；

—tk-1时刻同化更新后的状态变量；

模型参数；

（3）定义tk时刻的观测数据矩阵dobs,k：

式中：Hk—观测算子；

Strue,k—tk时刻真实状态向量；

ɛk—观测误差矩阵。

（4）利用观测数据进行同化更新：

—预测的状态矩阵；

Kk—卡尔曼增益矩阵；

Rk—观测误差协方差矩阵；

—状态误差协方差矩阵；

—预测的状态均值向量；

N—集合样本数目；

j—集合样本编号。

1.2 考虑预报偏差的迭代式集合卡尔曼滤波（Bias-CEnKF）

由于EnKF 在观测时间点对状态变量和模型参数同时做一次线性校正，没有考虑参数和变量之间的非线性关系，可能造成两者的不一致性。当考虑预报偏差后，偏差项也同时进行线性校正，进一步增加了不一致性。Wen 等[25]提出的迭代式集合卡尔曼滤波（Ensemble Kalman Filter with Confirming Option，CEn-KF）是一种从上一时刻到当前时刻的局部迭代方法，在保证计算效率的前提下能够有效降低不一致性影响，获得了广泛的应用[14，26-27]。本文采用该迭代式方法构建Bias-CEnKF 方法，相比于标准集合卡尔曼滤波，主要变化为：

（1）增加一个偏差项bk，将bk与状态变量mk、模型参数θk一起组成增广状态矩阵Sk，即式（1）修改为：

（2）对偏差项进行预报，并将其直接反馈至状态变量预报模型，对模型状态变量预测值进行修正，即式（2）修改为：

—tk-1时刻同化更新后的偏差项；

Λk—偏差项的时间相关系数；

wk—偏差噪声；

—tk-1时刻经过同化、重新预测后的状态变量。

（3）在式（4）中，偏差项与状态变量、模型参数一起进行同化更新，然后将更新后的返回至tk-1时刻，重新进行tk时刻的模型状态变量预测：

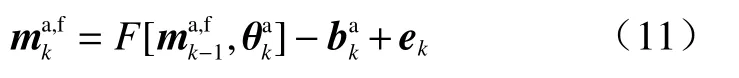
—tk时刻同化更新后的偏差项。

将f作为下一时段的初始状态变量，顺序开展数据同化。

2 算例

2.1 算例概况

如图1 所示，研究区为一个二维承压含水层。含水层东西方向长500 m，南北方向长300 m，垂向厚2 m，平面均匀离散成50×30 个网格。含水层东部和西部边界为定水头边界，水头值分别为100，103 m，南部和北部为隔水边界。含水层内有2 口抽水井和2 口注水井，自初始时刻开始运行，流量均恒定为100 m3/d。研究区共设置64 个水位（H）观测点（含抽、注水井所在位置），12 个对数渗透系数（Y）观测点。设定含水层渗透系数场（Y=lnK）服从对数正态分布，二阶平稳并可用二维可分离指数型协方差函数描述。真实Y场均值为0.5 m/d，标准差为1.2，x、y方向相关长度分别为120，60 m。采用Karhunen-Loeve(K-L)展开[28]生成一个对数渗透系数场，作为Y参考场，见图1（b）。该渗透系数场下含水层的初始流场为无其他干扰情况下水流达到稳定状态时的流场，见图1（a）。模型模拟期总时长10.0 d，分为20 个时段，时间步长0.5 d。采用MODFLOW 代码模拟真实的水流模型，获取水位观测点每个时段的水位观测数据[29]。模拟期前15 个时段的水位观测值用于数据同化，后5 个时段的水位观测值用于预测检验。

图1 研究区初始流场与观测位置和对数渗透系数Y 参考场（文献[26]有修改）Fig.1 Initial flow field and observation locations (a) and reference field of Y (b) (modified from Ref.[26])

2.2 情景设置

本次研究将对数渗透系数场作为未知参数，通过数据同化对其进行识别。同化系统中地下水水流模型概化存在不确定性，对模型初始条件、边界条件、源汇项的概化可能不准确，设置4 种情景：

情景1：真实地下水水流模型东西边界为定水头边界，同化系统中地下水水流模型东西边界为隔水边界。

情景2：真实地下水水流模型东部和西部边界水头值分别为100，103 m，同化系统中地下水水流模型的东部和西部边界分别为99.5，103.5 m。

情景3：真实地下水水流模型的初始流场见图1（a），同化系统中地下水水流模型的初始水头均设定为100 m。

情景4：真实地下水水流模型包含降雨入渗补给过程，入渗补给量0.001 m/d，同化系统中地下水水流模型未考虑降雨入渗补给过程。

2.3 参数设置

集合样本数目设置为500，经验证能够保证本文模拟结果的统计稳定性。初始Y场统计特征与真实场有一定差距，均值为0，标准差为1.1，代表对Y场的先验认知。水位观测点观测误差服从均值为0、方差为2.5×10-5的高斯分布。Y观测点观测误差服从均值为0、方差为1×10-6的高斯分布[10]。偏差噪声服从均值为0、方差为0.01，x和y方向相关长度分别为300，180 m 的空间相关高斯分布。偏差项的时间相关系数设置为0.99[24]。

2.4 数据同化实现过程

采用Bias-CEnKF 同化水位观测数据，识别对数渗透系数场的主要过程为：

①首先生成初始对数渗透系数场样本。

②针对每个渗透系数场，采用MODFLOW 计算得到时段末各网格点水位预报值。

③预报偏差项，并修正时段末各网格点水位预报结果。

④根据修正后的各网格点水位预报值集合，计算状态误差协方差矩阵、卡尔曼增益矩阵。

⑤利用本时段水位观测数据，同化更新各网格点对数渗透系数、水位、偏差项。

⑥重新返回到时段初，将同化更新后的对数渗透系数场代入MODFLOW 计算得到时段末各网格点水位值，利用更新后的偏差项予以修正。

⑦将修正后的各网格点水位值作为下一时段的初始状态变量，重复步骤②～⑦，至同化结束。

考虑预报偏差的集合卡尔曼滤波（Bias-EnKF）与Bias-CEnKF 相比，少了迭代过程，即无上述步骤⑥，直接采用同化更新后的水位作为下一时段的初始状态变量。标准EnKF 与Bias-CEnKF 相比，无偏差项，也无迭代过程。

2.5 同化效果评价标准

采用常用的均方根误差（RMSE）作为评价标准，RMSE越小，代表估计量与真实值越接近。RMSE计算公式为：

式中：M—网格点数目；

—网格点i处的集合均值；

—网格点i处的真实值。

3 结果

3.1 同化结果

采用标准EnKF、Bias-EnKF 和Bias-CEnKF 分别对设置的4 种情景进行数据同化。

图2 表示含水层Y场的同化结果与参考值的RMSE随同化时间的变化情况。EnKF 计算得到的RMSE均大于Bias-EnKF 和Bias-CEnKF 的计算结果，且对情景1、情景3 和情景4 而言，随着同化的进行，基于EnKF的RMSE逐渐增大或趋于一个较大值，说明滤波发散，集合未能收敛到一个合理的状态。而在4 种情景下，Bias-EnKF 和Bias-CEnKF 计算得到的RMSE均随着同化的进行逐步减小至稳定。在情景1 和情景2 下，随着同化步数的增加，Bias-CEnKF 的RMSE均小于Bias-EnKF。说明Bias-CEnKF 考虑了参数和变量的非线性关系，降低了两者的不一致性，同化效果优于Bias-EnKF。如对情景1 而言，Bias-EnKF 和Bias-CEnKF 计算得到的RMSE分别收敛到0.79，0.75。图3列举了情景1 下3 种方法同化得到的Y均值场。可以看出，在初始Y均值场比较均匀，与参考场（图1b），差距较大的情况下，EnKF 同化得到的Y均值场与参考场显著不同，而Bias-EnKF 和Bias-CEnKF 得到的Y均值场与参考场相似，基本反映了参考场的非均质分布特征。

图2 不同情景下含水层对数渗透系数场RMSE 变化情况Fig.2 RMSE of Y under different scenarios

图3 情景1 不同方法同化得到的对数渗透系数均值场Fig.3 Mean field of Y identified with different methods under scenario 1

图4 为含水层水头场的RMSE随同化时间的变化情况。与Y场同化效果类似，EnKF 同化得到的水头场RMSE最大。这表明存在模型预报偏差时，随着同化的进行，观测数据提供的信息不但未改善EnKF 的预测性能，而且对情景1 和情景4 而言，其对模型状态的刻画反而变得更差。相比之下，Bias-EnKF 和Bias-CEnKF 同化得到的水头场RMSE在同化的中后期趋于稳定，同化水头场与真实水头场接近。图5 列举了情景1 下含水层中几个代表性点的水头拟合结果。代表性点分别为靠近含水层西边界、中间和东边界处的点A（30 m，150 m）、B（250 m，150 m）和C（470 m，150 m）。可以看出，对靠近边界位置的点A 和点C，在同化初期，Bias-EnKF 和Bias-CEnKF 同化值与实际水头有一定差距，随着同化的进行，同化值与实际水头拟合效果较好，对中间位置的点B，Bias-EnKF 和Bias-CEnKF 同化过程中同化值与实际水头一直保持较好的一致性；而对EnKF 而言，点B 和点C 处的同化值与实际水头差距随着同化的进行并没有减小，反而有变大趋势。综合说明，考虑预报偏差后，含水层水头场的识别效果得到了有效提升。

图4 不同情景下含水层水头场RMSE 变化情况Fig.4 RMSE of H under different scenarios

图5 情景1 代表性点水头拟合结果对比Fig.5 Comparison of head-fitting results of the representative points under scenario 1

表1 为EnKF、Bias-EnKF 和Bias-CEnKF 同化末期的RMSE统计结果。与图3 和图4 综合分析，在情景1 下Y场和水头场的RMSE均最大，而情景4 下Y场和水头场的RMSE均最小。说明对本文研究问题而言，含水层边界性质的不准确刻画带来的预报偏差对同化结果的影响最大，降雨补给量的不准确刻画带来的预报偏差对同化结果的影响相对最小。就3 种方法同化效果而言，Bias-CEnKF 同化得到的RMSE均是最小的，表明其同化性能最好。

表1 EnKF、Bias-EnKF 和Bias-CEnKF 同化结果对比Table 1 Assimilation results of EnKF, Bias-EnKF and Bias-CEnKF

3.2 预测结果

因Bias-CEnKF 的同化性能最好，利用其同化结果，对后5 个时段的水头场进行预测，并综合分析同化阶段及预测阶段水头预测值与实际值的接近程度。同样，分别选取靠近含水层西边界、中间和东边界处的点A（30 m，150 m）、B（250 m，150 m）和C（470 m，150 m）作为观测点进行分析。如图6（a）—（c）所示，在情景1 下除边界处观测点A 和C 在同化前期水头预测值与实际值有一定差距外，其余时段水头预测值和实际值均拟合较好。同化前期观测点A 和C 处水头值与实际值差距较大是由于情景1 将模型东西边界误认为隔水边界，而边界性质对靠近边界位置处的水头影响较大所致。但是随着同化步数的增加，边界概化不准确的影响逐渐消失。在预测阶段不同观测点处水头预测结果均与实际水头值接近。图6（d）—（f）为情景2 下的水头拟合结果。与情景1 相比，不同阶段3 个观测点处的水头预测值均与实际值拟合较好。这说明相对边界性质而言，边界水头数值大小对同化效果的影响较小，同化前期可以通过偏差项弥补边界水头值误差带来的影响。图6（g）—（i）为情景3下的水头拟合结果。由于初始流场水头值统一设置为100 m，在同化初期对水头预测值也有较大影响。但是随着同化的进行，初始流场概化不准确带来的影响逐步减弱。图6（j）—（l）为情景4 下的水头拟合结果。受降雨补给影响，点B 处水头呈现逐渐增大趋势，边界处点A 和C 因为靠近定水头边界，受降雨补给的影响相对较小。但是不同观测点处同化和预测阶段的水头估计值与真实值均拟合得较好。

图6 不同观测点处水头预测值与实际值对比Fig.6 Predicted and observed head values at different observation locations

图7 为预测末期y=150 m 剖面处各点的水头预测值与实际值对比结果。4 种情景下水头实际值基本位于95%置信区间范围内，且除在高水头和低水头位置有一点差距外，水头预测均值与真实值均拟合较好。高水头和低水头位置处水头拟合结果稍差的原因主要是通过数据同化并未完全复制真实的Y场，而渗透系数空间变异性对水头的影响非常关键。

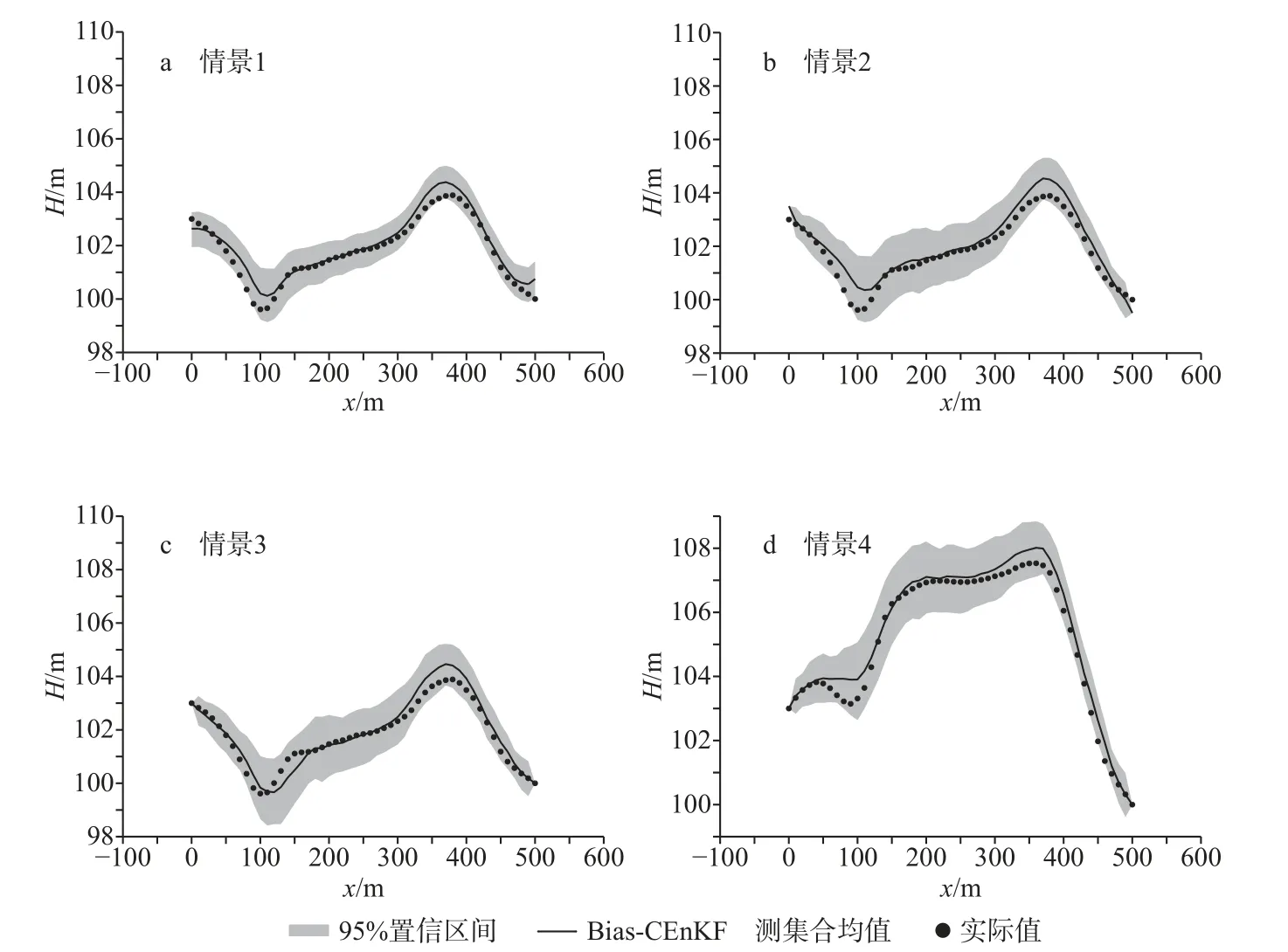
图7 预测末期y=150 m 剖面上水头预测值与实际值对比Fig.7 Predicted and observed head values in cross section y=150 m at the end of the prediction period

Bias-CEnKF 在同化初期的预测水头值可能和真实值有一定差距，但是同化中后期和预测阶段，水头真实值均在预测的置信区间范围内，且预测水头值均与真实值拟合较好。在同一剖面位置处，由于受到含水层渗透系数空间变异性的影响，在高水头及低水头点处的水位拟合效果稍微变差，但整体拟合结果较好。因此，Bias-CEnKF 方法可以很好地弥补模型概化不准确对水位预报带来的影响，具有较好的同化性能。

4 讨论

含水层Y场和水头场的同化结果表明，当模型概化不准确时，Bias-CEnKF 的同化性能显著优于EnKF，分析原因主要为前者利用偏差项对模型状态变量预测值进行了修正。因此，为说明不同情景下偏差项如何减小模型概化不准确带来的影响，对Bias-CEnKF 同化得到的偏差项结果作进一步分析。如图8 所示，情景1 的偏差整体呈现西北部和东南部为负值、西南部和东北部为正值的特征，且越靠近边界位置偏差越大。这是由于研究区西北部和东南部为抽水井，真实的定水头边界条件下，会引起边界水流补给含水层，而情景1 假定东西边界为隔水边界，无水流补给含水层，在系统同化过程中需要通过偏差项增加源项（负值）以弥补模型概化不准确的影响。同理，研究区西南部和东北部为注水井，真实的定水头边界条件下，会有水流通过定水头边界流出含水层，而情景1 假定边界为隔水边界，同化系统通过偏差项增加汇项（正值）以弥补模型概化不准确的影响。

图8 不同情景下Bias-CEnKF 同化得到的偏差项的均值场Fig.8 Mean field of bias corrections based on the Bias-CEnKF under different scenarios

情景2 的偏差整体呈现西部为正值、东部为负值、向中间位置趋于0 的特征。这是由于真实的西部边界水头为103 m，情景2 假定西部边界水头（103.5 m）高于真实水头值，系统同化过程中需要通过汇项（正值）降低高水头的影响。同理，真实的东部边界水头为100 m，情景2 假定东部边界水头（99.5 m）低于真实水头值，在系统同化过程中需要通过源项（负值）降低低水头的影响。此外，边界水头对含水层水头分布的影响通常表现为由边界向中间逐渐减弱的趋势。因此，偏差项也由边界向中间逐渐趋于0。

情景3 的偏差项无明显规律性。这是由于理论上初始水头对同化系统的影响在顺序数据同化过程中会逐渐减弱甚至消失，且初始水头不像边界或源汇项等给予含水层以持续的流入或流出影响。

情景4 的偏差基本为负值并由中间向边界逐渐趋于0。这是由于情景4 忽视了真实的降雨补给，同化系统需要通过源项（负值）体现降雨补给的影响。同时，越往边界受定水头边界影响越大，降雨补给影响相对减弱，因此，偏差也趋于0。

5 结论

（1）模型概化不确定条件下，模型概化不准确时，使用标准EnKF 进行数据同化，可能会导致滤波发散，造成同化失败，而Bias-CEnKF 能够识别得到接近于真实场的Y场和水头场，且其同化性能优于Bias-EnKF。

（2）Bias-CEnKF 同化系统中的偏差项在物理意义上相当于用源汇项弥补模型概化不准确带来的影响。对本文4 种情景而言，Bias-CEnKF 能够识别得到合理的偏差项分布特征。

（3）利用Bias-CEnKF 同化得到的状态变量、模型参数以及偏差项进行预测，均获得了可靠的预测结果。对于实际复杂问题，模型概化不准确对模拟结果的影响可能会随着时间增加而累积。要进行长期的合理预报，一方面应尽可能对地下水水流模型进行准确刻画，另一方面应及时采用最新观测数据进行同化更新，实时修正偏差项。