带投资的超额损失再保与障碍分红最优化

孙宗岐，杨鹏，吴静，杨阳

1）西京学院医学院，陕西西安 710123；2）西安财经大学统计学院，陕西西安 710100；3）西京学院理学院，陕西西安 710123

再保险策略作为一种转移保险公司索赔风险，提高保险公司对股东或被保险人分红能力的重要风险控制指标，在精算领域具有十分重要的研究价值．一般的再保险策略分为比例再保险和超额损失再保险两类．ASMUSSEN等［1］证明在带漂移的扩散模型中，超额损失再保险策略优于比例再保险策略；XU等［2］也证明在扩散风险模型下，期望值保费原理的超额损失再保策略较比例再保策略更优．

分红策略作为鼓励股东融资、激发被保险人投保热情的重要风险控制手段，是保险公司实务管理的重要抓手，也是精算领域的热门研究问题．基本的分红策略分为障碍分红和阈值分红，其共同点是财富超过分红界后才进行分红；区别在于阈值分红是有界速率的分红，而障碍分红是无界速率的分红．近年来，以最大化累积分红折现的期望函数为准则的研究成果日渐丰富，其中以最优障碍分红策略的研究最多［3-8］．

在考虑超额损失再保策略下的保险公司最优障碍分红的研究方面，YAN等［9］在对称风险信息下考虑带交易成本、残值及注资的最优障碍分红和超额损失再保问题；CHENG等［10］在再保保费非便宜的假设下，讨论扩散模型下的相同问题．但以上研究均未考虑保险盈余已经普遍投资于资本市场的现实，虽然已有考虑带风险资本投资的最优再保-障碍分红问题的相关报道［11-15］，但鉴于超额损失再保在数理计算中的复杂性，这些研究仅考虑了较为容易计算的比例再保问题，对于带投资的最优超额损失再保-障碍分红问题的研究鲜有报道．同时，保险实务中的任何保险赔付都有上限，一般研究中对赔付额分布的长尾假设也过于理想，考虑截尾分布才更能刻画赔付额的实际情况．市场摩擦的存在和破产清算时残值的分红也是保险实务的现实情形．

本研究考虑摩擦市场中带风险投资和终端残值的保险公司超额损失再保与障碍分红最优化问题，假设赔付额服从截尾分布，保险公司的盈余过程用扩散近似过程描述，通过使用随机最优控制原理及微积分方法求解最优超额损失再保策略、最优投资策略与最优障碍分红函数．

1 模型建立

本研究假设的随机过程和随机变量都定义在完备概率空间(Ω，Ft，P)上，产生的σ-域流{Ft：t＞0}完备且右连续．允许连续交易且资产可任意分割，有摩擦、自融资且无套利．

经典的Cramer-Ludberg盈余为

其中，x0为保险公司的初始盈余；c为保费率；Yi为第i次索赔时的索赔额，且E[Yi]＞0，是参数为λ的Poisson过程，表示到时刻t为止索赔发生的次数．保险公司按超额损失再保策略进行部分索赔风险的转移，即保险公司的实际赔付额为（∧表示两者取其小），其余的索赔部分转移至再保险公司赔付．设赔付额的分布函数为F(x)，定义为保险公司的最大赔付额度．赔付额的一阶矩二阶矩按期望值原理的保费率c=(1+θ)λE[Yi]，其中，θ是保费的安全负载系数．假设再保险的保费率为再保保费的安全负载系数为η(η≥θ)，于是盈余过程R(t)=x+ct-(1+此时，R(t)可以近似为扩散过程

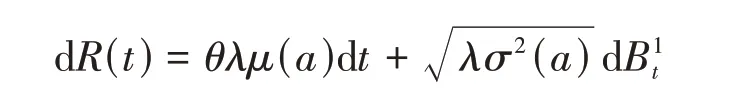
保险公司在破产前将部分盈余b(x)投资于价格p(t)满 足的 风 险 资 产（如股票），其中，也是一维标准布朗运动；相互独立．则财富过程满足

其中，Lt表示保险公司按照障碍分红策略在t时刻所得的累计红利．整理得保险公司的财富过程满足

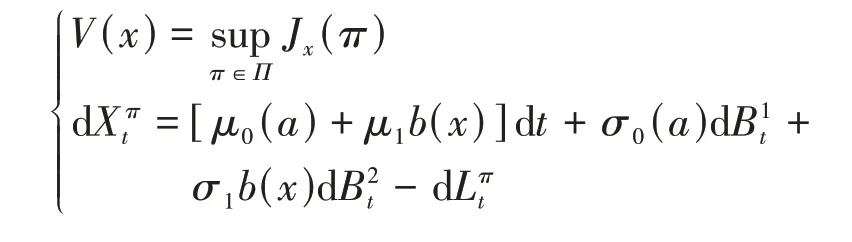
称V(x)为最优分红函数．假设V(x)是二次连续可微的函数，且V＇(x)＞0、V″(x)＜0．由随机最优控制原理［16］，将最优控制问题转化为如下Hamilton-Jacobi-Bellman（HJB）方程

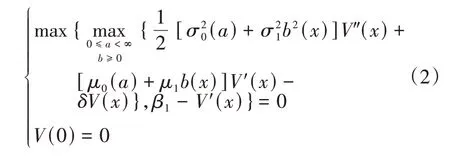
设x1=inf[x≥0|V＇(x)≤β1]为障碍分红的边界，即财富超过x1的部分被全部进行分红．

2 模型求解

为计算方便，假设θ=1、λ=1．当0≤x＜x1时，则HJB方程为

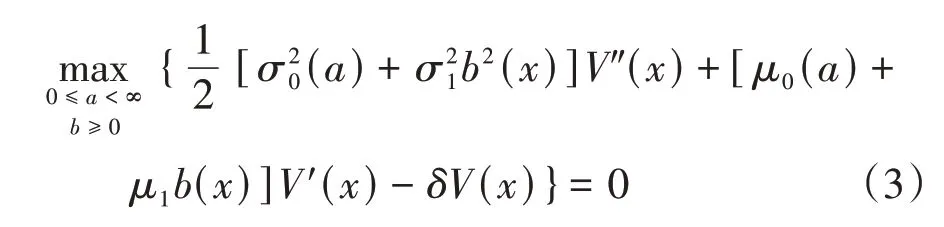
设最优策略为π*，为简化符号，以下取．由极值的必要条件可得

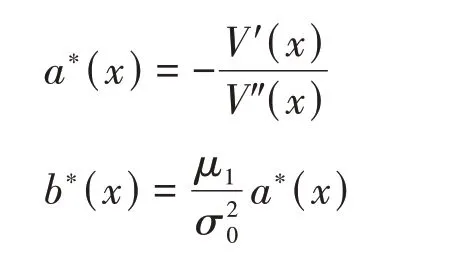
当a*(x)∈[0，M]时，将上述结果与V″(x)=一并代入式（3）有

两端关于x求导，并将代入，有

解之得

引理1设a*(x)是［0，+∞）上的连续可微函数，若a*(x)是 方 程（2）的 解，且a*(0)=0，则，且∀x＞0，都有a*(x)＞0．

【证】运用洛必达法则并结合a*(x)是［0，+∞）上连续可微的函数，易证Hamilton-Jacobi-Bellman方程

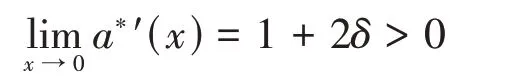
成立．

由此可知，存在ε＞0，当x∈(0，ε)时，有a*＇(x)＞0．设I(y)=2δy2+2μ(y)y-σ2(y)，则I(y)是［0，+∞）上连续函数，且I(0)=0，I＇(y)=4δy+2μ(y)，I″(y)=4δ+2-F(y)．显 然 当y＞0时，有I＇(y)＞0，I″(y)＞0．所以，I(y)是［0，+∞）上单调递增的连续凸函数．设u0=inf[x≥0|a*＇(x)=0]，下证u0=0．

假设u0≠0，由式（4）可知，a*＇(u0)=0蕴含着I(a*(u0))=0，由函数I(y)的性质可知必有a*(u0)=0．又因a*(x)在[0，u0]上可微，所以a*(x)在[0，u0]亦连续，据微分中值定理可知，存在z∈(0，u0)，使得a*＇(z)=0，这显然与u0的定义矛盾，即当x＞0时，a*＇(x)≠0．故∀x＞0，有a*＇(x)＞0．又由于a*(0)=0，所以，当x＞0时，a*(x)＞0．

令G(y)=+∞)，则当y＞0时，G＇(y)＞0，且当x＞0时，最优超额损失再保策略与最优投资策略为

由于当x＞0时a*＇(x)＞0，且a*(0)=0，则存在xM∈［0，+∞），使得a*(xM)=M．

命题1若x≥xM，则a*(x)≥M．

【证】假设存在使得设，则 结 合M的 定 义 可 知又 由a*(x)的 连 续 性，有且有a*(x)＜M．因 为 当y＞0时，G＇(y)＞0，所以G(y)是(0，+∞)上单调递增函数．进而对有G(a*(x))-G(M)=x-这与x的取法显然矛盾，故原命题成立．

根据问题的实际意义，当xM≤x＜x1时，取a*(x)=M，并在此条件下求解HJB方程的解．对于在[0，+∞)上二次连续可微的函数V(x)，将a*(x)=M代入

有

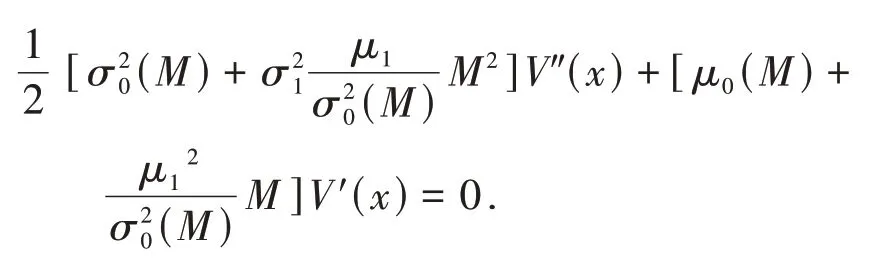
解该微分方程得

以下求解微分方程解中的任意常数k3和k4．由V＇(x1)=β1和V″(x1)=0可 得，

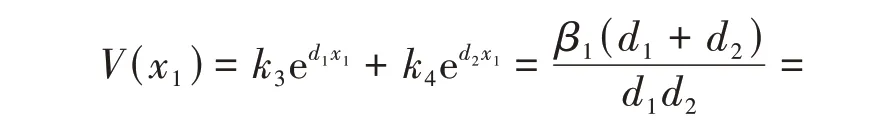
当x≥x1时，V(x)=x-x1+V(x1)，故再 由V(xM-0)=V(xM+0)、V＇(xM-0)=V＇(xM+0)有

解之得

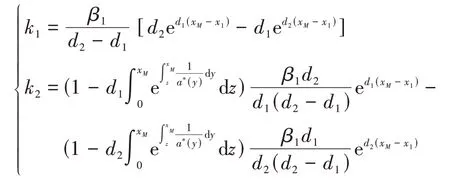
由V(0)=P可知k2=P．HJB方程（2）的解为

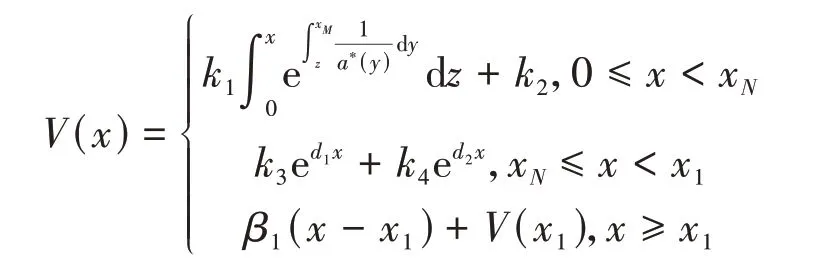
以下求解最优分红界．

引理2设

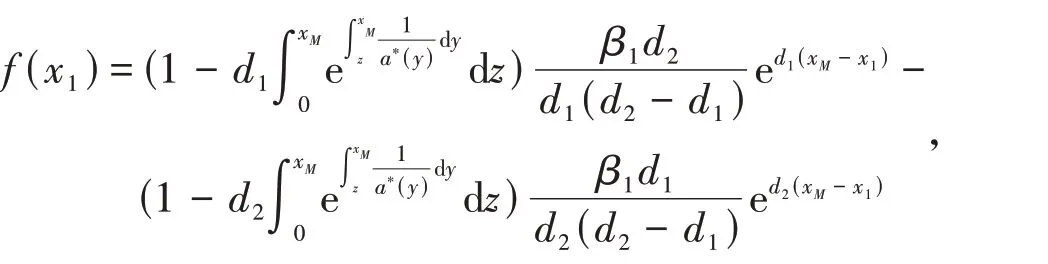
x1∈[xM，∞)，则存在唯一的使

【证】由于d1＜0＜d2，不难判断-∞．因为

又因为

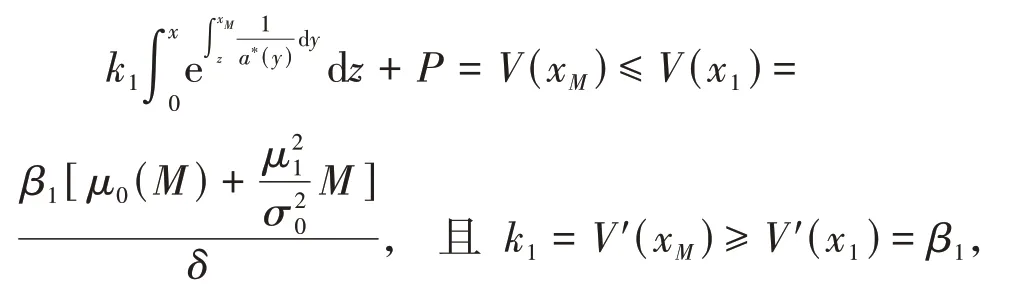
所以，f(xM)≥P．

因为

又因为d1＜0＜d2，且进而所以f＇(x1)＜0．故存在唯使得

定理1设如上文，则HJB方程（2）的解

在[0，+∞)上二次连续可微的凹函数．

【证】因为k1＞0、k2＞0、k3＜0＜k4，所以当0≤x＜xM时，当时，进而当时，有而时，有V″(x)=0，所以V(x)是在［0，+∞）上二次连续可微的凹函数．

结语

本研究将赔付额由长尾分布的假设修正为有赔付上限的截尾分布，并考虑较难进行数理推导的超额损失再保险策略下的保险公司最优障碍分红问题，以及保险公司破产清算时的终端残值、风险资本投资行为和分红时市场摩擦等条件．在便宜再保保费的特殊情形下，运用随机最优控制原理将保险公司的最优控制问题转化为HJB方程，通过数理推导和证明，得到最优超额损失再保险策略、最优投资策略、最优障碍分红界限及最优分红函数．

本研究还存在一定不足，如实际保险实务中再保保费并不是便宜的；尚未通过具体的截尾分布对本研究结论进行数值分析；阈值分红作为一种更加保守分红，带投资的最优超额损失-阈值分红问题仍有待讨论．这些问题是下一步研究的重点．