基于排序网络的奇数大数逻辑门电路设计

王艳, 张楠, 郭靖

(1. 中北大学 电子测试技术国防重点实验室, 太原 030051；2.仪器科学与动态测试教育部重点实验室, 太原 030051)

0 引 言

高能辐射粒子在入射到SRAM存储器敏感单元的过程中会产生电子-空穴对[1]，在电场作用下，存储器敏感单元可以将这些电子-空穴对收集起来，并发生电荷积累。若积累的电荷超过临界电荷值[2]，该存储节点的电势将会发生改变，同时引发逻辑电平值的改变，最终发生单粒子翻转(Single Event Upset，SEU)现象[3]。SEU不会产生永久的错误，在存储器的下一个写入阶段，重新写入的值可以恢复这些错误。因此，SEU又被称为软错误(Soft Error)。

在微处理芯片内，存储器占总面积的30% 左右，因而存储器中发生的软错误将会直接影响芯片的功能。因此，可以通过加强存储器的抗SEU能力来提高微处理芯片的可靠性。存储器的抗SEU加固设计有许多种，错误纠错码(Error Correction Code，ECC)是其中之一[4]，其主要是通过ECC编译码的方式对存储器进行加固[5]。随着集成电路技术的发展，一次单粒子事件会引起多个单元同时翻转(Multiple-Cell Upset，MCU)，而为了纠正MCU，就需要使用纠正能力更强的ECC[6]，但是其编译码方式将会越来越复杂，硬件开销也将随之增加。

一步大数逻辑可译码(One-Step Majority Logic Decodable，OS-MLD)可以使用一步大数逻辑译码器来进行译码，因此其译码程序和电路都非常简单，这些码包括差异集(Difference Set Code，DS)，低密度奇偶校验(Euclidean Geometry Low Density Parity Check Code，EG-LDPC)和正交拉丁方(Orthogonal Latin Squares，OLS)[7]；其中，由于DS码的复杂度低、速度快，且拥有更长的信息位，因此被广泛的应用于对存储器进行MCU的纠错保护。以(73, 45)DS码为例，来解释一步大数逻辑译码器的工作原理(见图1)。译码时，首先将码长为73位的DS码(包含45个信息位)存入移位寄存器中[8]；然后，根据相应的9组奇偶校验组合对寄存器中数据进行错误检测和纠正：

(1)如寄存器中C72发生了翻转，则9组奇偶校验组合通过异或门输出的 γ0～ γ8中将有多数个1；此时，大数逻辑门(Majority Logic Gate，MLG)将输出大数值1；C72与MLG输出值1异或，从而纠正C72并输出该值；

(2)如寄存器中C72没有发生翻转，仍保持其正确的值，则9组奇偶校验组合通过异或门输出的 γ0～ γ8中将有多数个0；此时，MLG的输出值为0；将C72与MLG输出值相比较，异或结果为0，表示该码位没有发生翻转。

由此可见，MLG是OS-MLD译码器的重要组成部分，其性能和硬件开销直接决定了一步大数逻辑译码器电路的复杂程度和硬件开销。

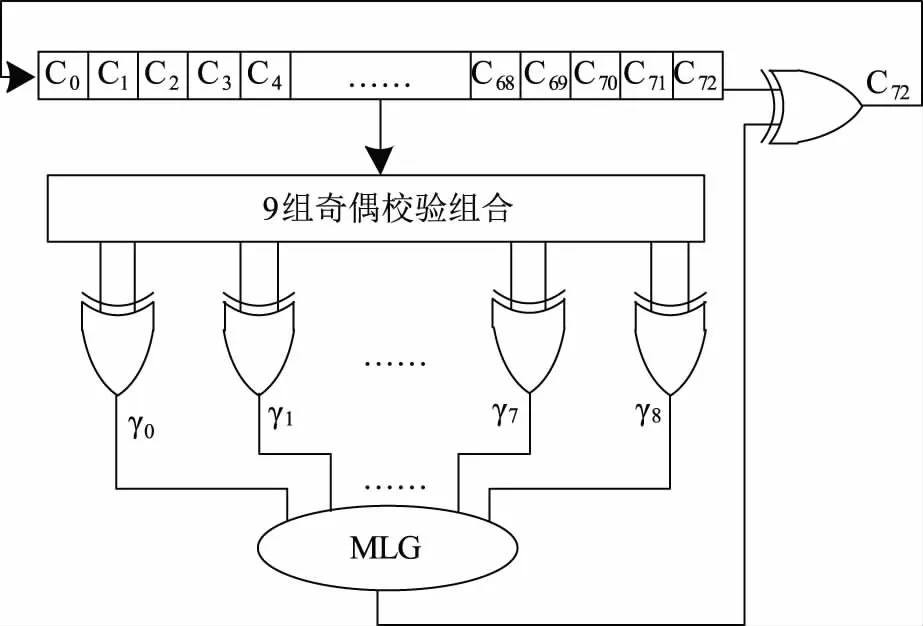
图1 (73, 45)DS码的工作原理

1 MLG电路设计

1.1 传统MLG电路

在OS-MLD译码器中，MLG电路可以评估奇偶校验和的大数值，然后根据该大数值来准确的判断译码位是否发生了错误：若该译码位为错误码位，则可实现对该码位的纠正。MLG电路的具体功能如下：当输入向量的值多数为1时，则输出大数值为1；当输入向量的值多数为0时，则输出大数值为0；若输入向量的个数为偶数，且输入向量0的个数与向量1的个数相等，则输出大数值为0。传统MLG电路的构造方法为：

(1)假设输入向量为γ0 ～γθ-1，θ为MLG电路输入向量的个数；

(2)从γ0 ～γθ-1中选取ω个输入向量，则共有种组合方式(若θ为偶数，ω=2-1θ+1；若θ为奇数，ω=2-1(θ+1))；

(3)根据组合方式列出相应逻辑表达式，从而输出大数逻辑值。

传统的5输入MLG电路如图2所示：如输入向量为 γ0 ～γ4，然后选取其中3个向量，则共有10种组合方式(“+”表示或门)：

Oout=γ0γ1γ2+γ0γ1γ3+γ0γ1γ4+γ0γ2γ3+γ0γ2γ4+γ0γ3γ4+γ1γ2γ3+γ1γ2γ4+γ1γ3γ4+γ2γ3γ4

(1)

由式(1)可知，5输入传统MLG电路需要29个两输入逻辑门。同理，6输入传统MLG电路需要59个两输入逻辑门；8输入传统MLG电路需要279个两输入逻辑门；9输入传统MLG电路需要629个两输入逻辑门。对比5、6、8、9输入的传统MLG电路可知，随着输入向量个数的增加，MLG的硬件开销呈现指数增长的态势。

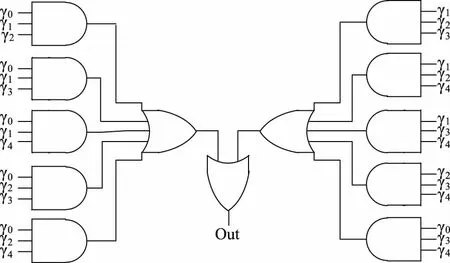
图2 传统5输入MLG电路

1.2 基于排序网络的MLG电路

为了解决传统MLG电路硬件开销大的问题，文献[9]提出了一种基于排序网络的MLG电路的构造方法。在计算机系统中，排序网络用于将输入数据重新排序，且排序过程与数据序列是相互独立的。数据序列的排序由“黑盒”实现，在左侧输入原始序列，在右侧输出生成的新序列，从而实现对输入序列从大到小的排序，即若输入序列为10101011，则输出序列为11111000。然而，随着排序网络输入向量个数的增加，其电路的复杂程度也将会极大地增加，进而导致硬件开销也增加很多。

针对这一问题，文献[9]提出了一种基于排序网络的MLG电路构造方法。假设输入向量的个数为θ(θ为偶数)，构造MLG电路则需要2个2-1θ输入的排序网络、2-1θ个两输入与门、1个2-1θ输入或门。基于排序网络的8输入MLG电路如图3所示，该电路将一个8输入MLG电路拆分为两个4输入的排序网络[9]，对排序后的两组向量进行比较(第一组第1个值与第二组第4个值比较，第一组第2个值与第二组第3个值比较，以此类推)，最后将比较后的值进行或运算，进而输出正确的大数逻辑值。

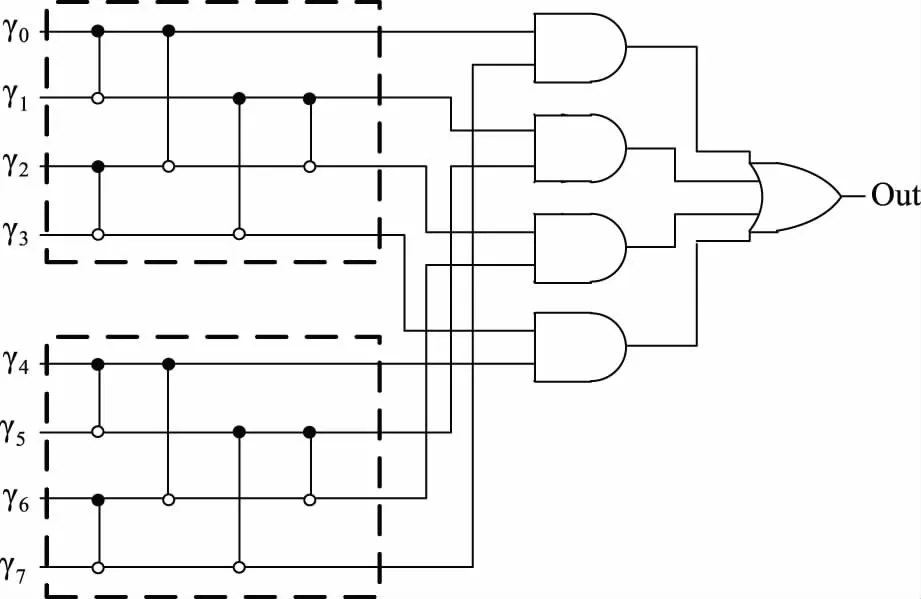
图3 文献[9]构造的8输入MLG电路

表1给出了文献[9]构造的MLG电路逻辑门的使用数量，相比于传统MLG电路，基于排序网络的6输入MLG电路使用的两输入与门减少了80.0%，两输入或门减少了42.8%；基于排序网络的8输入MLG电路使用的两输入与门减少了93.7%，两输入或门减少了76.3%。

文献[9]仅构造了偶数输入的MLG电路，而DS码需要奇数输入的MLG电路来进行译码，表2所示为(21, 11)和(73, 45)的DS码表。为此，文献[10]提出了奇数输入的MLG电路的构造方法，如图4所示。该电路将9输入的排序网络拆分为两个4输入的排序网络，排序后通过组合逻辑电路输出大数逻辑值。但是，这种构造方法存在错误，并不能正确的输出大数逻辑值：若输入向量γ0～ γ8为000011111时，MLG电路的大数输出值应为1，但文献[10]中构造的9输入MLG电路的大数逻辑输出值实际为0。因此，该电路不能对所有输入情况执行正确的大数逻辑输出。

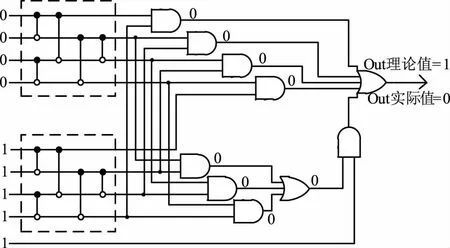
图4 文献[10]中构造的9输入MLG电路

1.3 本文构造的MLG电路

本文针对文献[10]中存在的问题，提出了一种新型奇数输入的MLG电路构造方法。该MLG电路以排序网络为基础，其具体构造步骤如下：

(1)假设输入向量为γ0～ γθ-1，θ为MLG的输入向量的个数；

(2)根据其大数阈值2-1(θ+1)，将输入拆分为两部分，分别使用2-1(θ+1)输入的排序网络和2-1(θ-1)输入的排序网络；

(3)对2-1(θ+1)输入的排序网络排序后的输出与2-1(θ-1)输入的排序网络排序后的输出使用组合逻辑电路来输出大数逻辑值。

本文以5输入MLG电路的构造方法为例，解释其构造过程：

(1)假设输入向量为γ0～ γ4，θ=5，则其大数阈值为2-1(θ+1)=3；

(2)使用一个2-1(θ+1)=3输入的排序网络和一个2-1(θ-1)=2输入的排序网络来进行排序；

(3)对两个排序网络的输出使用组合逻辑电路来输出大数逻辑值。

本文以5输入MLG电路的构造方法为例，解释其构造过程：

(1)假设输入向量为γ0～ γ4，θ=5，则其大数阈值为2-1(θ+1)=3；

(2)使用一个2-1(θ+1)=3输入的排序网络和一个2-1(θ-1)=2输入的排序网络来对输入向量进行排序；

(3)对两个排序网络的输出使用组合逻辑电路来输出大数逻辑值。

图5中，当输入γ0～ γ4为01111时，对γ0～ γ1排序，输出α0～ α1(10)，对γ2～ γ4排序，输出ε0～ ε2(111)；之后，α0、ε1通过与门，输出1；α1、ε0通过与门，输出0；最后，1、0、ε3(1)通过或门，输出大数逻辑值1。对其他输入进行类似分析，证明本文提出的5输入MLG电路可对所有输入情况正确实现大数逻辑的功能。

图5 本文构造的5输入MLG电路

本文构造的9输入MLG电路如图6所示：当输入γ0～ γ8为000011111时，构造的MLG电路可以正确的输出大数逻辑值0。因此，文章提出的基于排序网络构造的奇数输入的MLG电路可以正确的实现大数逻辑的功能。

图6 本文构造的9输入MLG电路

表3给出了本文构造的MLG电路逻辑门的使用数量。由表3可得，相比于传统MLG电路，本文构造的5输入MLG电路使用的两输入与门减少了70.0%，两输入或门减少了33.3%；本文构造的9输入MLG电路使用的两输入与门减少了96.4%，两输入或门减少了86.4%。

2 功能验证及硬件开销比较

采用Xilinx的FPGA-XC6SLX16进行功能验证，利用Verilog硬件描述语言对本文构造的5输入和9输入MLG电路进行功能验证。图7为本文构造的5输入MLG电路的功能仿真图：若输入向量γ0 ～γ4为10100，输出大数逻辑值为0；若输入向量为10101，输出大数逻辑值为1。图8为本文构造的9输入MLG电路的功能仿真图：若输入向量γ0 ～γ8为000011111，输出大数逻辑值为1；若输入向量为000011110，输出大数逻辑值为0。这些仿真结果表明，本文构造的新型MLG电路能够实现正确的大数逻辑功能。

图7 本文构造的5输入MLG电路仿真结果

图8 本文构造的9输入MLG电路仿真结果

表4给出了在FPGA上使用传统MLG电路和本文构造的MLG电路实现DS码译码器的硬件开销。相比于使用传统MLG电路，(21，11)DS码译码器在使用本文构造的5输入MLG电路时，Slices减少了28.5%，逻辑延时减少了17.3%，6-LUT减少了21.7%，Flip-Flops减少了19.4%；(73，45)DS码译码器在使用本文构造的9输入MLG电路时，Slices减少了80.7%，逻辑延时减少了63.6%，6输入LUT减少了78.0%，Flip-Flops减少了74.3%。

3 结束语

文章使用排序网络构造了一种新型奇数输入的大数逻辑门电路，可有效减少逻辑门的使用数量，并降低电路的逻辑延时、Slices、Flip-Flops、LUT等。因此，DS码译码器可使用本文构造的MLG电路来进行译码操作，进而可降低加固存储器时所带来的硬件开销。