基于改进BP神经网络的低压配电台区智能电能表误差状态评估模型

刘文宇, 刘璐，刘馨然，崔赫，李运泽

(国网辽宁省电力有限公司营销服务中心， 沈阳 110000)

0 引 言

智能电能表是配电网台区中重要的电能计量设备，是智能配电网的重要组成部分[1-3]。智能电能表运行的准确性直接影响到电网公司与用电用户之间的电能交易与结算过程的真实性和公平性。同时电网公司对于保障智能电网准确运行也关系着防止漏电、窃电等不正当行为的检测，直接影响到电网公司运营的经济指标[4-5]。然而传统的对智能电能表运行误差检测由于缺乏有效的智能手段，只能采用定期上门抽检的形式，这样的方式面临着检测效率低下，检测范围覆盖面低，检测成本高等缺点。

随着包括高级量测技术(Advanced Metering Infrastructure，AMI)在内的智能技术发展，配电网近年来也正经历着智能化升级和改造的过程，这使得对智能电能表运行误差的检验手段不断升级[6-7]。在这样的情形下，电网公司一方面实现了对智能电能表运行状态的远程采集和分析，另一方面也积累了海量的智能电网运行数据。如何从这些数据中提取出智能电网运行的关键信息，判断其运行误差的合理性，对于电网公司实现全面漏电，窃电的检测以及智能电能表的更新有着重要的作用。

在这方面目前已有较多文献进行了智能电能表误差估计方法的建模。比如文献[8]提出了基于限定记忆递推最小二乘算法的智能电能表运行误差估计模型，该模型能够有效提升评估的覆盖范围，同时评估的实时性得到了显著提升，为电网公司及时发现异常智能电能表提供了技术支撑。文献[9]首先建立智能电能表运行误差估计的多元线性评估方程，基于改进经典吉洪诺夫正则化算法进行模型求解，有效提升了评估的精准性。文献[10]计及了用户用电水平，智能电能表安装数量和位置等因素建立了一套智能电能表运行误差估计模型，实现了对智能电能表误差状态的准确检测。文献[11]通过将读数矩阵进行分解的方式对所建立的智能电能表运行误差方程进行求解，并计及了广义能量守恒方程。此外，还有一些文献则是将灰色关联分析法[12-13]、局部异常因子算法[14]，支持向量机算法[15]等方法用于构建智能电能表运行误差估计模型。然而目前还很少有文献基于智能算法优化神经网络法构建智能电能表运行误差估计模型。

BP 神经网络是用于前向多层网络的学习算法[16-17]，智能电能表运行误差估计作为一个面向海量历史数据的问题，通过对BP神经网络的训练能够获得较优的评估网络，并将该网络应用于对测试数据的评估。而传统BP神经网络隐含层节点数一般采用经验公式设定，缺乏合理的灵活性，对BP神经网络中引入对隐含层节点数的粒子群算法优化过程，能够提升网络的性能。

本文提出了一种基于粒子群优化BP神经网络提出智能电能表误差估计方法。该方法首先分析了训练数量的搜集过程以及对历史数据的预处理，剔除不合理的数据。接着通过对BP神经网络中隐含层节点数引入粒子群算法进行优化，得到基于粒子群优化BP神经网络的智能电能表误差估计流程。最后通过一个算例验证了所提出模型的有效性和合理性。

1 智能电能表误差估计模型

1.1 数据搜集

采用BP神经网络进行智能电能表误差估计需要确定网络的输入层数据和输出层数据。其中输入层数据选取为智能电能表的用电信息数据和电量计量数据。用电信息数据包括用户编号、智能电能表型号、负载率、供电半径、用户类型；电量计量数据为该智能电能表采集到的历史电量数据，通过高级量测体系(Advanced Metering Infrastructure，AMI)采集得到，采样频率为15 min/次。而输出数据即为智能电能表的误差百分比参数。

然而由于历史上对智能电能表的传统检测方法采用抽样检测进行，因此所有误差数据的输出数据中只有一部分智能电能表具有准确的误差数据。对于历史检测智能电能表采用误差检测结果作为其误差数据。而对于其他电能表采用总智能电能表的误差作为其误差数据。总电能表和其他电能表的网络关系如图1所示。

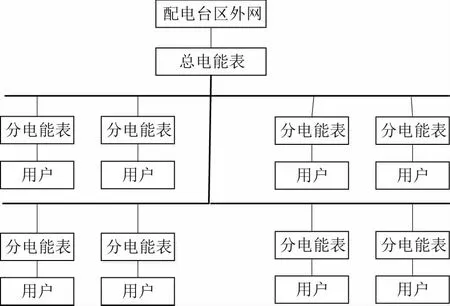
图1 配电台区总电能表和分电能表分布示意图

式中y0(t)为总电能表在t时段的读数;ξ0(t)为总电能表的相对误差；N为配电网中分电能表的数量；yi(t)为第i个分电能表在t时段的读数；ξi(t)为第i个分电能表在t时段相对误差；yloss(t)为t时段配电网实际网损功率。

由于总电能表和分电能表的读数在历史运行经验上存在如式(2)所示的近似关系，可以推导得到如式(3)所示的总电能表和分电能表相对误差关系。

式(3)说明对于训练数据中未进行历史检验的智能电能表采用总智能表的相对误差数据即可有效进行表征。从而弥补了部分智能电能表历史运行数据缺失的问题。

1.2 数据预处理

智能电能表的运行误差受到其负载率的影响较大。当智能电能表负载率较低时，由于智能电能表本身存在的潜供电流以及电压互感器非线性区间的影响，导致智能电能表的运行误差较大。

因此在神经网络训练之前需要对负载率较低的智能电能表数据进行剔除。智能电能表运行负载率的定义如式(4)所示。

式中θi(t)为第i个分电能表在t时段的负载率；Ii(t)为第i个分电能表在t时段的检测负载电流；IN,i为第i个分电能表的额定电流。

对于负载率在10%以下的智能电能表电量数据从训练样本中进行剔除。

2 粒子群优化BP神经网络

2.1 BP神经网络原理

基本BP神经网络包括两个方面：信号的前向传播和误差的反向传播[18]。BP神经网络的结构如图2所示。

BP神经网络算法的执行步骤如下：

(1)对权系数Wij置初值。其中Wi,n+1=-θ。

(2)输入一个样本X=(X1,X2,…Xn,1)，以及对应期望输出Y=(Y1,Y2,…,Yn)。

(3)对于第k层第i个神经元的输出Xik，基于如式(5)所示的过程。

(4)求各层的学习误差对于输出层有k=m，则有式(6)。

对于其他各层则有如式(7)所示的计算。

(5)修正权系数Wij和阀值θ。使用权值修正公式如式(8)所示。

(6)当求出了各层各个权系数之后，可按给定指标判别是否满足要求，模型中采用期望误差指标的收敛精度作为判别指标。

如果满足要求，则算法结束；如果未满足要求，则返回步骤(3)执行。以上过程针对任意Xp=(Xp1,Xp2,…,Xpn,1)和Yp=(Yp1,Yp2,…,Ypn,1)进行。

图2 单隐含层的BP网络基本结构图

2.2 基于粒子群算法的隐含层节点数量优化

一般来说，BP神经网络的隐含层采用单层的形式，这主要是因为单隐含层的BP神经网络足以模拟任何非线性映射关系，达到对输入层和输出层的数据关系训练效果。隐含层节点数的确定通常采用经验公式进行确定，然而这样的隐含层节点数量制定方式存在诸多的局限性。一方面如果节点数量过少，将无法有效模拟输入层和输出层之间的关系，而当节点数量过多时，尽管对输入层和输出层关系的拟合效果很好，但很可能会出现过拟合的现象，过拟合将导致对新的输入数据进行神经网络求解时出现偏差较大的情况。

因此本节针对BP神经网络隐含层节点数基于训练数据对采用粒子群算法进行优化，得到最优的隐含层节点数量作为神经网络的参数，进而对数据进行再次训练得到所需要的神经网络结构。粒子群算法速度和位置的更新方法如式(9)和式(10)所示[19-20]。

式中i为粒序号，i=1,2,…,Np，Np为粒子种群数目；s为迭代代数；为第i个粒子s代的个体极值点；gbests为种群到s代的全局极值点；和分别为第i个粒子在第s+1代和第s代的速度；和分别为第i个粒子在第s+1代和第s代的位置；c1、c2为学习因子；r1、r2为[0，1]之间的均匀分布随机数。

则可以得到基于粒子群算法的BP神经网络隐含层节点优化流程如下：

(1)制定粒子群算法参数，包括种群个数、粒子位置维数、学习因子、惯性权重、最大迭代数。令当前迭代次数为零。

(2)按照如式(11)所示的神经网络隐含层节点数的经验公式,以初始节点数数据作为粒子位置初始化得到L=[L(i)]，其中L为以L0为均值，以n2为方差的正态分布进行随机模拟并取整得到。

L0=2n+1

(11)

式中n为输入层节点数、根据输入数据种类:用户编号、智能电能表型号、负载率、供电半径、用户类型、电量计量数据制定，n取6，则L0取13。

(3)基于训练样本数据针对每个粒子的L(i)进行训练，对每个隐含层神经元的权系数进行训练，得到第i个粒子的期望误差信号ζ(i)。

(4)以期望误差信号的倒数1/ζ(i)作为粒子适应度函数，适应度函数最大的粒子xgbest作为当前最优解，记录每个粒子的历史最优解，基于式进行粒子位置和速度的更新，更新全局历史最优解和个体历史最优解。

(5)判断迭代次数是否达到了最大迭代次数，如果是则算法结束，输出当前全局最优粒子的隐含层节点数，否则令迭代次数加1。返回步骤(3)。

2.3 基于粒子群优化BP神经网络的智能电能表误差估计步骤

基于所建立的智能电能表误差估计模型以及粒子群优化BP神经网络，可以得到智能电能表误差估计步骤流程图如图3所示。

图3 基于粒子群优化BP神经网络的智能电能表误差估计流程图

3 算例

针对某地区典型配电网台区中智能电网运行误差估计问题，采用本文所建立的方法进行评估。该配电网台区配置了一台总智能电能表以及163台分智能电能表。训练数据采用2020年1月到5月的智能电能表历史运行数据，包括输入数据用户编号、智能电能表型号、负载率、供电半径、用户类型、电量计量数据以及输出数据运行误差百分比，采样频率为15min/次；样本测验数据采用2020年6月1日到15日的智能电网运行输入数据。分别针对AFPM型和PZ型两种型号的智能电能表进行运行误差评估，以上两种智能电能表已经广泛应用与居民负荷以及商业负荷的电能计量领域。

同时构建一个多层BP神经网络，该网络具有一个输入层，一个输出层，一个隐含层，其中输入层节点数为6，输出层节点数为1，隐含层节点数采用粒子群算法进行优化。设定第一层隐层神经元的阀值函数为logsig函数，设定第二层隐层神经元的阀值函数为purelin函数。设置BP神经网络最大迭代次数为200代，训练的误差要求为0.000 1。粒子群算法优化中，隐含层节点数初始值为13，算法最大迭代次数为180代，两个学习因子均为0.8，惯性权重系数为0.5，最优隐含层节点数训练数据采用2020年1月智能电能表运行数据。

首先运行包含BP神经网络训练过程的隐含层节点数粒子群算法优化过程，得到最优隐含层节点数的收敛曲线如图4所示。同时得到随着隐含层节点数的变化，神经网络的误差指标收敛值的收敛曲线如图5所示。

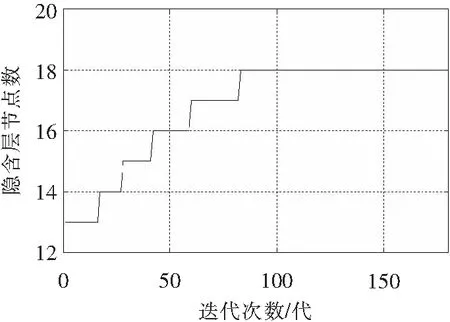
图4 基于粒子群优化算法的BP神经网络隐含层节点数收敛曲线

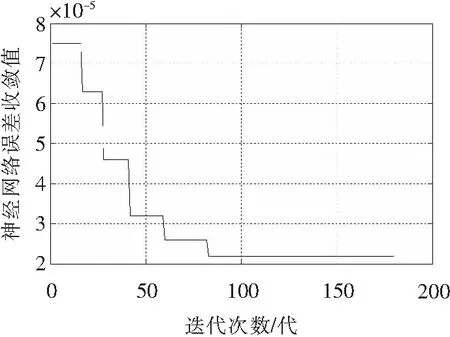
图5 基于粒子群优化算法的BP神经网络误差指标收敛值变化曲线

从图4和图5中可以看出，BP神经网络隐含层节点数从初始设置的经验值13个逐渐收敛到了18个，同时BP神经网络误差收敛值从0.007535%逐渐下降到了0.002241%，因此将隐含层节点数设置为18个。

采用训练完成的BP神经网络对测试样本进行评估，任取2020年6月1日到15日内某一个采样时刻,将智能电能表运行误差情况针对电能表编号进行统计得到图6。

图6 某采样时刻配电台区智能电能表误差分布情况

事实上，依据BP神经网络对测验数据的评估结果该配电网台区内智能电能表误差具体情况如表1所示。

从表1可以看出，编号为26号，74号和153号智能电能表运行发生了负超差，可能是因为电能表发生了故障或者向其他用户实行了窃电行为；而编号为68号，118号的智能电能表发生了正超差，可能是因为电能表发生了故障或者该用户被漏电和窃电。

以AFPM型智能电能表为例，为了验证粒子群优化BP神经网络相比于传统的BP神经网络在智能电能表运行误差估计中的优势，针对同样的训练数据和测验数据，分别采用传统BP神经网络以及本文粒子群优化BP神经网络进行运行误差评估，形成运行指标对比如表2所示。

从表2中可以看出，基于传统BP神经网络的误差在第16代达到了收敛目标，而基于粒子群优化BP神经网络的误差在第9代即达到了收敛目标，说明了改进的有效性。

4 结束语

本文提出了基于粒子群优化BP神经网络的智能电能表运行误差估计方法，该方法通过对BP神经网络中隐含层节点数引入粒子群算法进行优化，并基于优化后的BP神经网络对智能电能表历史运行数据进行训练，得到BP神经网络,对测试项目进行测试，从而对智能电能表运行误差进行评估，发现台区中运行异常的智能电能表。通过基于粒子群优化BP神经网络的智能电能表运行误差估计方法能够为配电网台区中智能电能表的故障检测、漏电窃电事件发掘提供指导。相比于传统BP神经网络，本文粒子群优化BP神经网络在收敛性能上更优，有助于提升智能电能表运行误差估计的实时性。