基于改进BPSO算法的含微网的配电网故障恢复方法研究

李豪，马驰，孙菊，邱灿，朱骏骋，廖泳

(国网湖北鄂州市供电公司，湖北 鄂州 436000)

0 引 言

根据我国双碳目标，2030年达到碳峰值，2060年实现碳中和，加快发展清洁能源，实现绿色生活方式[1]。微网的接入使配电网结构和运行方法都产生了较大变化，配电网作为连接电网和用户的桥梁，其故障会造成较大的经济损失和社会影响[2]。故障恢复作为其关键技术之一，关系到系统运行的可靠性，已成为一个重要的研究课题。

目前，国内外许多研究人员在故障恢复模型求解领域进行了大量的研究，包括启发式算法[3]、遗传算法[4]、禁忌搜索算法[5]、蚁群算法[6]等。在文献[7]中，将两步优化方法用于配电网故障恢复。结果表明，考虑节点价格机制的方案优于不考虑节点价格机制的方案，表明所建立的模型可以降低故障时的失电负荷，提高系统的可靠性。在文献[8]中，将多级优化方法用于配电网(含DG)的故障恢复。结果表明，所提方法在较为复杂的电网中可以合理进行规划，且兼顾了故障恢复速度。在文献[9]中，以故障恢复的最小失电负荷为目标函数建立故障恢复模型，通过yalmip软件进行求解。结果表明，与传统方法相比，所提方法可以快速和有效的恢复失电负荷。在文献[10]中，提出了一种基于重构的分层响应故障恢复方法，该方法使用双种群交叉算法来寻找恢复方案。结果表明，与传统方法相比，所提方法即保证了快速性，且恢复方案较为优越。但是，上述故障恢复方法的运行速度较慢，在发生大规模故障时恢复的失电负荷较少，适应性有待进一步提高。

基于此，以最小网损、最少开关动作次数和最少失电量为目标函数建立了含微网的配电网故障恢复模型，将改进二进制粒子群优化(Binary Particle Swarm Optimization , BPSO)算法和遗传算法(Genetic Algorithm,GA)相结合用于模型求解。通过仿真对故障状态进行对比分析。

1 故障恢复模型

1.1 目标函数

在故障恢复中，大量负荷需要恢复供电。为了延长开关的使用寿命，其操作次数必须减少。恢复后网损小等要求。本文以最小网损、最少开关动作次数和和最少失电量为目标函数。

(1) 最小网损。

网损最小的目标函数如式(1)所示[11]。

(1)

式中Ih为支路的集合；Pl、Ql、Ul、Rl分别为支路l的有功、无功、电压和电阻。

(2) 失电量最小。

最少失电量目标函数如式(2)所示[12]。

minL=∑ωiPi

(2)

式中Pi、ωi分别为节点i的负荷有功和开关状态(ωi=1闭合，ωi=0断开)。

(3)开关操作次数。

最少开关动作次数目标函数如式(3)所示[13]。

(3)

式中Sn为开关n的当前状态；Sn0为开关n的初始状态；N为开关动作次数。

本文提出的配电网故障恢复模型有三个目标函数。为了方便求解，采用加权后的目标函数将多目标问题转换为单目标优化问题进行求解，如式(4)所示。

(4)

式中a、b、c分别为最小网损、最少失电量和最小开关动作次数的权重系数，a+b+c=1；P′为总恢复负荷量；L′为总失电量；S′为开关的总数。

恢复原则为：对失电负荷尽可能多的恢复。开关动作次数尽可能少，优先动作故障区较近的开关。恢复后系统网损尽可能小。

1.2 约束条件

目标函数约束包括馈线容量、节点电压、功率平衡和微网功率约束等。

(1)馈线容量不应超过支路允许的最大值，馈线容量的约束如式(5)所示[14]。

Sij≤Sijmax

(5)

式中Sij和Sijmax分别为支路ij的当前功率和最大允许功率。

(2)节点电压要限制在一定范围内，约束如式(6)所示[15]。

Umin≤Ui≤Umax

(6)

式中Umin和Umax分别为节点的最小和最大电压。

(3)对于整个系统，功率不得小于系统负荷和网损之和，并且必须满足式(7)和(8)所示的平衡约束[16]。

(7)

(8)

式中PDGi和QDGi分别为微络接入节点i的有功和无功功率；PLi和QLi分别为节点i负荷的有功功率和无功功率 ；Ui和Uj分别为节点i和j的电压；Gij、Bij、θij分别为支路ij的电导、导纳和相差角；m为连接节点i的支路数。

(4)微网的功率约束如式(9)和(10)所示[17]。

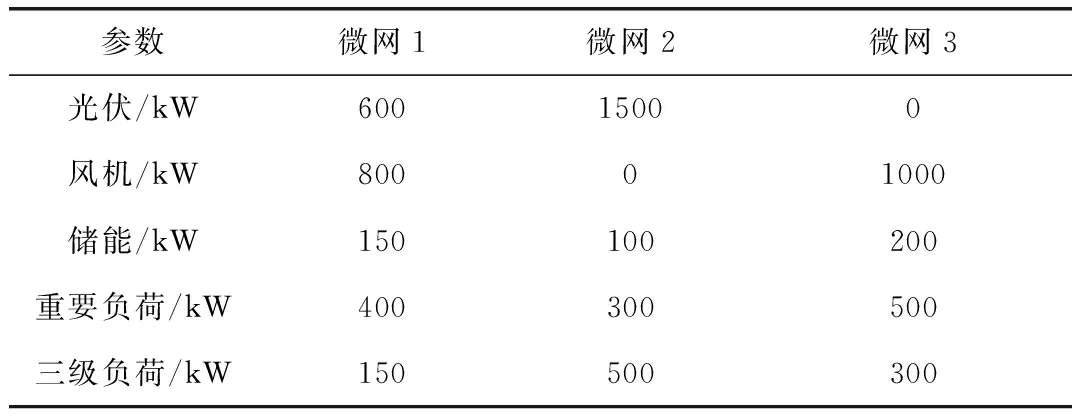
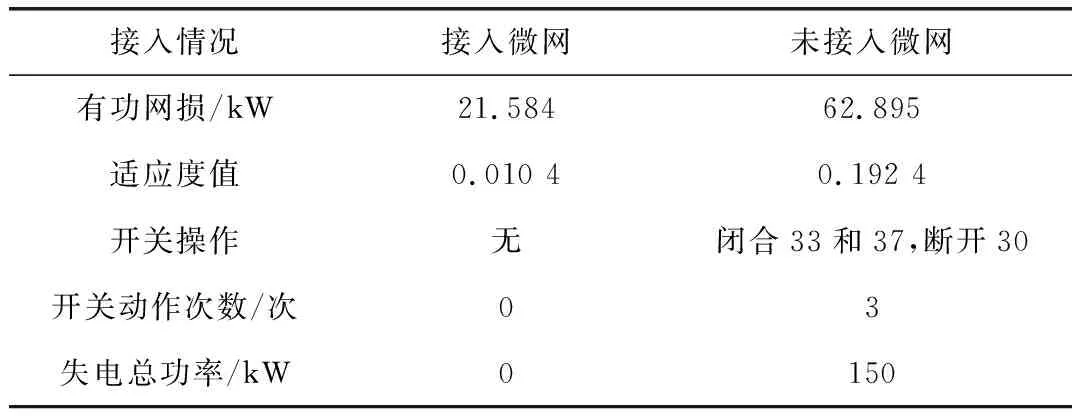
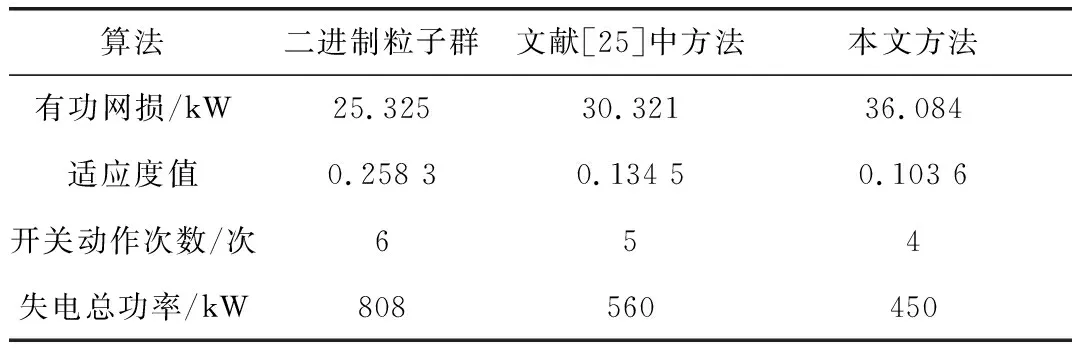
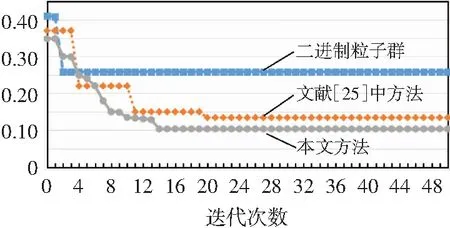
PDGmin

(9)

QDGmin

(10)

式中PDGmin和PDGmax分别为微网接入节点i的最小和最大有功功率；QDGmin和QDGmax分别为微网接入节点i的无功最小值和最大值。

2 配电网故障恢复

2.1 改进二进制粒子群算法

配电网的故障恢复是采用开关操作来求解最佳故障恢复方案，二进制粒子群优化算法适用于这种离散空间优化问题[18]。

BPSO算法位置更新如式(11)和(12)所示[19]。

(11)

(12)

(13)

在二进制粒子群优化算法中，迭代中可能会有“早熟”问题，本文对适应度值f进行调整，将粒子i的适应度值fi与平均适应度值favg做差，与均方差σ进行比较，粒子更新如式(14)所示[20]。

(14)

式中Xpbest和Xgbest分别为个体和全局最优；k为迭代次数；ω为惯性权重。

ω越高，全局搜索能力越强。ω越小，局部搜索能力越强。随着迭代次数的增加，问题的细节也随之增加，在ω定值求解过程中会出现很多缺陷。因此，引入可变惯性重量，如式(15)所示[21]。

(15)

式中λ为权重因子，经过试验取0.01；N为粒子数。

2.2 引入遗传算法

在改进的BPSO中，粒子容易“早熟”，并在重复过程中陷入局部最优[22]。本文通过遗传操作生成一个新的种群，两种算法的结合可以相互取长补短[23]。通过方差σ2对适应度值进行调整，在通过遗传操作生产新的种群，增强全局的搜索能力，从而解决“早熟”问题。适应度方差如式(16)所示。

(16)

式中fs为适应度值的归一化因子。fs如式(17)所示。

fs=max{1,max|fi-favg|}

(17)

fi与favg的差越小，方差σ2越小，变异概率如式(18)所示。

Pm=Pmin+(Pmax-Pmin)(1-σ2/N)

(18)

式中Pmin和Pmax分别表示变异的最大概率和最小概率；Pm在[0,1]之间。

2.3 故障恢复

故障恢复流程图如图1所示。

图1 故障恢复流程图

故障恢复步骤如下：

步骤1：输入配电网系统数据，对BPSO算法进行初始化，生成初始种群;

步骤2：更新粒子的速度和位置;

步骤3：保证配电网的辐射状，如果某支路被检查多次，对环网中一条支路进行切除，保证配电网的辐射状[24];

步骤4：失电区域是否有出力微网。如果有，执行下一步。如果没有，转至步骤6，并用联络线恢复供电[24];

步骤5：对没有故障的失电负荷进行记录，判断失电区域的微网能否恢复所有失电负荷的供电。如果可以，转到步骤7。如果不能，对孤岛进行划分;

步骤6：进行潮流计算，并验证约束。 不符合要求，切断负荷;

步骤7：计算f和σ2，判断是否为局部最优。为局部最优则进行变异操作，更新粒子位置，转到步骤2。否则，执行下一步;

步骤8：确定个体和全局最优位置;

步骤9：符合终止要求则输出结果，否则调整参数转到步骤2。

3 结果与分析

3.1 仿真参数

为了验证故障恢复方法优越性和可行性，以IEEE 33为例进行验证，通过MATLAB进行仿真。如图2所示的IEEE 33节点配电系统，系统由33个节点和5个联络支路(分别为33、34、35、36和37)组成。额定电压12.66 kV，各联络线备用容量300 kW，总负荷有功功率和无功功率分别为3175 kW和2300 kvar。本文算法参数：粒子数N=40、惯性权重0.4≤ω≤0.9、学习因子c1=c2=2、最大重复次数k=50、变异概率0.1。表1为微网参数，表2为节点负荷划分。

图2 33节点配电系统

表1 微网参数

表2 负荷划分

3.2 仿真分析

永久性故障发生在支路28时，首先对支路28进行隔离。无故障停电区域为：微网1和节点(28、29、30、31和32)，功率为620 kW。微网1的输出功率为1 000 kW，大于分支28故障的总失电负荷功率。微网1为节点28、29、30、31和32供电。此时，无需改变原有的配电网结构。实际上这是一个求解最优潮流的问题。将本文方法用于故障恢复，并与未接入微网的配电网结果进行对比，如表3所示。

表3 结果对比1

从表3可以看出，微网故障恢复方式不需要切换操作，网络结构保持不变，因此可以相对较快地恢复供电。在未接入微网的情况下，采用联络线进行供电恢复，开关闭合33和37，断开30，成本和时间都有所提升。接入微网的配电网有功网损也较优，且适应度函数的适应值也相对较小，恢复效果较好。图3为含微网的配电网故障恢复前后电压分布。

从图3可以看出，故障后,通过本文方法恢复故障，节点电压普遍高于故障前,故障修复前最小电压为节点17的0.902 9 pu，故障修复后,节点17的电压变为0.982 1 pu，从整体上提高了电压水平。

永久性故障发生在支路2时，发生大面积停电，首先对支路2进行隔离。无故障停电区域为：微网1-3和节点(2-32)，总失电负荷功率为3 165 kW。

对孤岛进行划分，优先恢复1级负荷，如有必要可切除3级负荷。表4为含微网和无微网配电网故障恢复结果的比较。

表4 结果对比2

从表4可以看出，在未接入微网的情况下，大面积停电采用联络线进行供电恢复，闭合4、36，断开7、11、16，恢复供电负荷较少，有功网损较大，适应值较大，故障恢复效果差。当采用微网进行故障恢复时，重要负荷都恢复了供电，开关的操作次数减少，恢复供电时间缩短，有功网损降低到36.084 kW，适应度值从0.545 3降低到0.103 6，有较好的故障恢复效果。

以上述故障为例(支路2故障)，分别将BPSO、文献[25]的改进PSO算法和本文算法用于故障恢复。如表5所示不同方法的恢复结果对比，如图4所示不同方法的适应度值随迭代次数的变化曲线。

从表5可以看出，本文方法失电负荷最少、开关动作次数最少，虽然有功网损不是最低，但停电支路都是三级负荷，恢复效果最好。文献[25]具有中等恢复效果。BPSO算法的恢复效果最差，存在许多未恢复的供电支路。

表5 不同算法的恢复结果对比

从图4中可以看出，标准BPSO算法的收敛效果最差，陷入局部最优解。文献[25]中方法检索精度低，效果中等。本文方法对BPSO算法进行了多次改进，不管是搜索能力还是收敛性都较强。

图4 不同方法收敛曲线

4 结束语

提出了一种含微网的配电网故障恢复方法。以网损最小、开关动作次数最少、失电量最少为目标，建立了含微网的配电网故障恢复模型，并将改进BPSO与GA相结合求解该模型。结果表明，微网可以恢复重要负荷的供电，开关操作次数少，缩短停电时间，有效降低网损。相比于传统方法，所提方法恢复供电时间短，恢复效果好。但本文也存在一些不足，在考虑微网的输出时处于稳定状态，但实际输出不一定稳定。在此基础上，逐步完善和改进将成为下一步研究的重点。