对2022年浙江省数学高考第20题的分析与研究
2022-11-22童益民
童益民
(效实中学,浙江 宁波 315012)
1 原题呈现与分析
例1已知等差数列{an}的首项a1=-1,公差d>1,记{an}的前n项和为Sn(其中n∈N*).
1)若S4-2a2a3+6=0,求Sn;
2)若对每个n∈N*,存在实数cn,使an+cn,an+1+4cn,an+2+15cn成等比数列,求d的取值范围.
(2022年浙江省数学高考试题第20题)
分析该题以等差数列为背景,第1)小题主要考查了等差数列的通项公式与前n项和公式,属于简单题;第2)小题主要考查了方程有解问题与不等式恒成立问题,有一定的灵活性,运算上有一定的复杂性,理解上有一定的综合性,属于中档偏难的题目.接下来对第2)小题进行分析与研究.
2 解题思路与分析
根据题意,对每个n∈N*,存在实数cn,使an+cn,an+1+4cn,an+2+15cn成等比数列,即对每个n∈N*,存在实数cn,使
(an+cn)(an+2+15cn)=(an+1+4cn)2
成立,即对每个n∈N*,关于cn的二次方程
有解,即对每个n∈N*,
(1)
恒成立.
分析1第2)小题的题意是双重有解与恒成立问题,结构是“对任意n∈N*,存在cn,使得p(n,cn)条件成立”.这里需要注意的是处理顺序上应先处理靠近条件p(n,cn)的量词,即先处理存在实数cn,使an+cn,an+1+4cn,an+2+15cn成等比数列;再处理远离条件p(n,cn)的量词,即再处理对每个n∈N*,式(1)恒成立,处理顺序上不能调换,可参考文献[1].
因为首项a1=-1,要求d的取值范围,所以用d来表示式(1).
方法1式(1)可化为
Δ={8(-1+nd)-15[-1+(n-1)d]-[-1+(n+1)d]}2-4{(-1+nd)2-[-1+(n-1)d][-1+(n+1)d]}≥0,
即
Δ=(-8nd+14d+8)2-4d2≥0,
亦即
(nd-2d-1)(2nd-3d-2)≥0.
(2)
方法2式(1)可化为
即
Δ=(-8an+1+14d)2-4d2≥0,
亦即
(an+1-2d)(2an+1-3d)≥0,
亦即
(nd-2d-1)(2nd-3d-2)≥0.
分析2在对式(1)的处理上,方法1与方法2殊途同归,方法1直接通过首项a1与公差d运算,方法2通过第n+1项an+1与公差d运算.相比较而言,方法1比方法2在运算上稍显复杂.
接下来再继续处理对每个n∈N*,式(2)恒成立.
方法1用特殊值代入法.
当n=1时,(d-2d-1)(2d-3d-2)≥0,即
(d+1)(d+2)≥0.
当n=2时,(2d-2d-1)(4d-3d-2)≥0,即
d≤2,
从而
1 当n≥3时,因为 nd-2d-1≥3d-2d-1=d-1>0, 2nd-3d-2≥6d-3d-2=3d-2>0, 所以 (nd-2d-1)(2nd-3d-2)≥0. 综上所述,1 方法2用函数图像法. 令f(n)=(nd-2d-1)(2nd-3d-2) 则f(n)≥0对n∈N*恒成立.因为d>1,所以 根据f(n)的图像(如图1),可得 图1 解得 0 从而 1 方法3用参数分离法. 式(2)可化为 [d(n-2)-1][d(2n-3)-2]≥0. 当n=2时,d≤2. 当n≠2时, 因为(n-2)(2n-3)>0,所以 即 图2 图3 综上所述,1 方法4用集合思想. 式(2)可化为 (2022年宁波效实中学高三数学模拟卷第17题) [3x(t-1)-1]·[log3(4x-1)-log3(4t)]≥0 对任意的正整数x恒成立,即不等式 [3x(t-1)-1]·(4x-1-4t)≥0(其中t>0) 对任意的正整数x恒成立. 当x=1时,[3(t-1)-1]·(4-1-4t)≥0,从而 当x=2时,[9(t-1)-1]·(8-1-4t)≥0,即 从而 当x≥3时, 故[3x(t-1)-1]·(4x-1-4t)≥0恒成立. (2022年杭州高级中学高三数学模拟卷第17题) 图4 根据平面区域,当 从而 故 (a·b)min=|OA|·|OB|cos∠AOB 当 例1中出现的字母较多,还涉及双重有解与恒成立问题,并且计算较复杂,对学生来说还是有一定的难度.需要学生能理解问题的本质,有较强的计算能力,能熟练处理有解与恒成立问题.这需要在平时的教学中,进一步发展学生的数学运算能力,对于有解与恒成立等基本问题,能够系统全面地掌握,形成规范化思考问题的品质.例2和例3得分较低,主要体现在学生不能找到处理恒成立问题的有效方法,习惯于用参数分离法、图像法和最值法处理恒成立问题,而例2用特殊值法先求必要条件再证充分性的思想让学生耳目一新,例3更是把一维的数集推广到二维的点集,用集合的思想方法让学生如雷贯耳,正如在黑暗中出现的一道闪电,让学生豁然开朗.基于对学生数学核心素养的培养,教师可从高考题中发现基本问题,再进行拓展研究,以此强化学生的“四基”,提高学生的“四能”,切实落实好课程目标.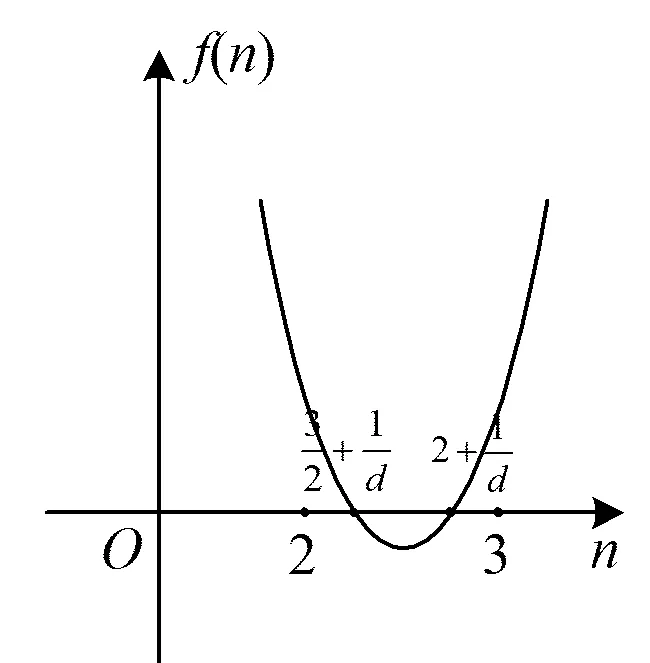



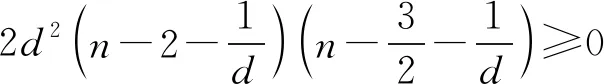
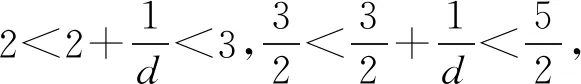
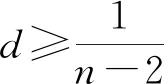
3 拓展应用


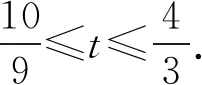
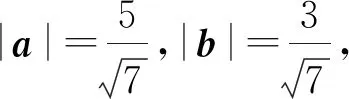




4 回顾总结
