固体材料的塑性功率方程与后继屈服函数
2022-11-22陈敬虞
陈敬虞
(嘉兴学院 建筑工程学院,浙江嘉兴314001)
对固体材料的塑性屈服研究由来已久,研究发现,一类固体材料的塑性屈服与静水压力无关,如碳钢、铜、铝等金属材料;另一类固体材料的塑性屈服与静水压力相关,如岩石、混凝土、土体等材料,而两类固体材料的初始屈服函数和后继屈服函数都是不同的.[1]
20世纪80年代,随着热现象和力现象耦合关系的研究进展,欧洲一些学者通过吸收不可逆过程热力学理论和理性热力学理论的合理成分,形成了较完善的内变量热力学理论(Thermo-dynamics with Internal Variables,T.I.V).近年来,内变量热力学理论所取得的成果丰富和发展了连续介质力学本构关系理论,使人们从物理学能量耗散的角度深入了解不可逆过程现象的物理本质,为研究建立连续介质的本构关系模型提供了新的思路和方法.现代塑性理论是通过引入内变量来描述固体材料在发生塑性变形过程中,固体材料内部细观结构的变化,用内变量作为自变量表示塑性应变、后继屈服函数、塑性势函数和自由能函数等.[2-8]
本文依据现代内变量塑性理论,给出塑性屈服与静水压力无关和塑性屈服与静水压力有关的两类固体材料的塑性功率方程,并由塑性功率方程得到用内变量表示两类固体材料的后继屈服函数(加载函数),并建立了塑性功率方程与后继屈服函数的联系,总结出由固体材料塑性功率方程得到后继屈服函数的方法.
1 固体材料的塑性功率方程或塑性功方程
连续介质热力学理论给出的可变形连续体,在等温变形过程中的热力学第一定律的微分形式为
(1)

(2)
将式(2)代入式(1),得
(3)

(4)

(5)

式(4)和式(5)联立,得
(6)
式(6)称为由内变量表示的连续变形体塑性功率方程或塑性功方程.
2 塑性屈服与静水压力无关的固体材料的塑性功率方程与后继屈服函数
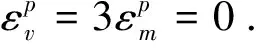
(7)
固体材料的后继屈服是很复杂的问题,目前,塑性力学理论依据许多金属材料的实验结果给出了加载面(后继屈服面)的3种模型,即等向强化模型、随动强化模型和组合强化模型.下面分别给出这3种模型对应的塑性功率方程,并由塑性功率方程推导出3种模型对应的后继屈服函数.
2.1 加载面等向强化模型的塑性功率方程和后继屈服函数
加载面等向强化模型理论认为,材料在某一方向荷载下发生强化后,则在相反方向必有相同程度的强化,即后继屈服面在应力空间中的中心位置及形状保持不变,只是随着塑性变形增大而逐渐等向扩大.
当塑性屈服与静水压力无关时,具有等向强化特性的固体材料的塑性功率方程有如下形式:
(8)

(9)
定义函数
(10)
(11)
由式(11)就可得到具有等向强化特性固体材料的加载函数或后继屈服函数
(12)
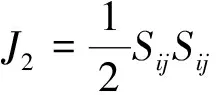
2.2 加载面随动强化模型的塑性功率方程和后继屈服函数
加载面随动强化模型理论认为,在塑性变形的过程中,屈服面的大小和形状都不改变,只是在应力空间做刚性移动,即屈服面的中心位置随塑性变形而变化.该模型在一定程度上可以反映许多金属材料的包辛格效应.
当塑性屈服与静水压力无关时,具有随动强化特性的固体材料塑性功率方程可表示为
(13)
其中αij(ξβ)是由内变量ξβ决定的背应力,k0是初始屈服等效应力的一个常数.由塑性功率方程决定的塑性功率函数可表示为

图1 加载面的三种强化模型
(14)
(15)
由式(15)可得到具有随动强化特性固体材料的后继屈服函数或加载函数为
(16)
2.3 加载面组合强化模型的塑性功率方程和后继屈服函数
加载面组合强化模型理论认为,在塑性变形的过程中,屈服面的形状、大小和位置都随内变量ξβ的演化而变化,组合强化模型可以更好地反映许多金属材料的塑性变形过程的包辛格效应.塑性屈服与静水压力无关的材料,其后继屈服函数对应的加载面的3种强化模型如图1所示.
当塑性屈服与静水压力无关时,具有组合强化特性的固体材料的塑性功率方程可表示为
(17)
则由塑性功率方程决定的塑性功率函数为
(18)
(19)
由式(19)就可得到具有组合强化特性固体材料的后继屈服函数或加载函数为:
(20)
3 塑性屈服与静水压力有关的固体材料的塑性功率方程和后继屈服函数
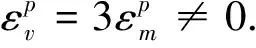
土体是由固体颗粒、颗粒间孔隙中的水和空气组成的混合物.土体在排水条件下,在比较大的压力作用下孔隙比减小,压力撤去后会残留较大的塑性体积变形,是典型的塑性屈服与静水压力有关的固体材料.由式(6)可得此类固体材料的塑性功率方程为
(21)
下面给出土体在常规三轴应力状态(二向应力状态)和三向应力状态下,用内变量表示的塑性功率方程和后继屈服函数.
3.1 土体在常规三轴应力状态下的塑性功率方程和后继屈服函数
英国剑桥大学的Thurairajiah博士通过剑桥黏土和砂土的系列常规三轴压缩实验的数据分析,得到了土体在常规三轴压缩应力状态下的塑性功率方程,为剑桥本构模型的建立奠定了重要基础.随后Roscoe&Burland对Thurairajiah博士的模型进行了修正,并建立了土体弹塑性本构关系的修正剑桥模型.Collins等利用内变量热力学理论,对修正剑桥模型进行分析,给出土体在常规三轴应力状态下的塑性功率方程为[10]
(22)
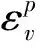
(23)
由式(22)和式(23),得塑性功率函数为
联立上面的两个方程,得到土体在常规三轴应力状态下的后继屈服函数为
(24)
(25)

图2 修正剑桥模型加载面随内变量的演化
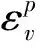
3.2 土体在三向应力状态下的塑性功率方程和后继屈服函数
依据塑性功率方程式(17)和土体在常规三轴应力状态下的塑性耗散函数式(23),假设塑性屈服与静水压力有关的固体材料一般在三向应力状态下的塑性耗散函数为
(26)
联立式(21)、式(26),可得塑性屈服与静水压力有关的固体材料的塑性功率方程:
(27)
由塑性功率方程得到的塑性功率函数为
(28)
联立上面两式,可得包含应力和内变量的后继屈服函数的表达式为
(29)
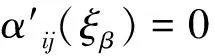
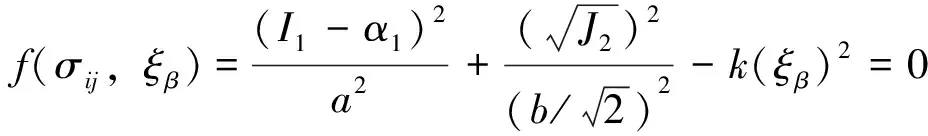
(30)
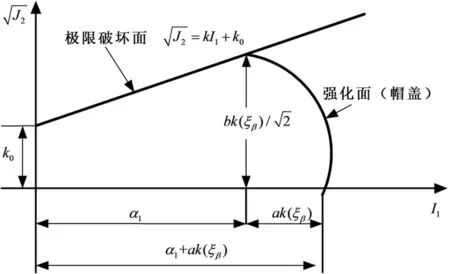
图3 黏土帽盖本构模型加载面
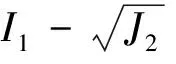
4 结论
塑性屈服与静水压力无关、塑性屈服与静水压力有关的两类固体材料的塑性功率方程是不同的.本文依据内变量塑性理论,给出两类固体材料的塑性功率方程,并通过数学演绎得到了固体材料的后继屈服函数:
第一,塑性屈服与静水压力无关的固体材料的塑性功率方程为
(31)
式(31)是塑性屈服与静水压力无关的固体材料加载面(后继屈服面)的组合强化模型的塑性功率方程,当k(ξβ)=k0为常数时,就是随动强化模型对应的塑性功率方程;当αij(ξβ)=0,就是各向同性强化模型对应的塑性功率方程.
第二,塑性屈服与静水压力有关的固体材料的塑性功率方程为
(32)
第三,由塑性功率方程得到塑性功率函数为
(33)
f(σij,ξβ)=0
(34)

