基于中心节点和社区吸引力的重叠社区识别算法
2022-11-22姚继强邓琨刘星妍赵阳朱莹凡欣
姚继强,邓琨,刘星妍,赵阳,朱莹,凡欣
(1.浙江师范大学 数学与计算机科学学院,浙江金华 321004;2.嘉兴学院:a.信息科学与工程学院,b.浙江省医学电子与数字健康重点实验室,c.外国语学院,d.材料与纺织工程学院,浙江嘉兴 314001)
世界上的复杂系统通常能够形式化成复杂网络,[1]如人与人之间的社交网络、[2]疫情传播网络等.分析复杂网络发现,网络中存在社区结构特性,通常表现为社区内部节点连接紧密、社区之间节点连接稀疏的特点,而在现实世界的网络中,社区结构通常表现出重叠性,即网络中存在部分节点同时属于多个社区,这类节点称为重叠节点,而这种社区结构叫做重叠社区.[3]本文将讨论的是复杂网络重叠社区识别,也就是识别出不同复杂网络中的重叠社区结构,其对于掌握现实网络中的结构特征和运行机理具有重要现实意义,并被广泛应用于舆情分析与控制[4]、内容推荐[5]、网络信息通信[6]等方面.
1 研究基础与CDCNCA算法简介
1.1 研究基础
近年来,学者提出了许多优秀的重叠社区识别算法.首先,基于标签传播的COPRA算法为每个节点初始化标签以及隶属度系数,并根据邻居节点的标签和隶属度系数更新标签,当所有节点的标签不再变化后算法结束,此时,具有相同标签的节点为同一社区,具有多个标签的节点为重叠节点;[7]基于上述算法,Ding等利用节点度和邻居度之和计算节点密度,并将密度较大的节点作为社区中心节点,然后采用基于邻居信息的多标签传播策略更新标签,从而找到社区结构.[8]基于团渗透的CPM算法致力于寻找网络中的完全子图,并通过团渗透的方式识别社区;[9]基于这一算法,Yan等找到了网络中的完全子图并将其作为初始核心,然后合并相似度较高的初始核心以产生社区核心,通过适应度函数将社区核心扩展成社区.[10]基于边聚类的LC算法则利用边属于单个社区的性质,以另一个角度识别社区,通过计算边之间相似度,构造边社区层次树,并以D函数切割层次树,从而实现最优社区划分;[11]基于此算法,Chen等将原始网络结构转换为链接网络,利用改进的距离动力学模型发现链接网络的非重叠社区结构,并将其转换为原始网络的重叠社区结构,从而完成社区识别任务.[12]
基于种子的局部扩展算法通常从网络的种子节点或者种子社区开始,利用网络局部信息识别社区.LFM算法随机选取未归属社区的节点作为种子,以节点提高社区的适应度值作为加入社区的评判标准,以此将种子扩展成社区.[13]这种以随机节点作为种子的方式,会导致所识别社区不稳定.GCE算法则用较小完全子图作为种子,对适应度函数进行贪婪优化,以此发现重叠社区.[14]此种采用完全子图作为种子的方式,使其在寻找种子阶段时间复杂度较高,并对网络结构要求严格,不适用于规模较大的稀疏网络.利用半局部相似度对网络边进行加权,根据边的总权重求得节点强度,将节点强度最大的节点作为种子节点,可不断优化归属度函数并将种子节点扩展成社区.[15]该算法在社区扩展时只考虑相邻节点,但往往单靠一阶邻居节点不足以充分利用网络结构信息,从而降低了社区识别效率.[16]将节点度数作为中心节点的评价指标,并以此构建种子进行社区识别,此算法将节点度中心性高的节点作为种子节点,可能并不适合应用在社区识别领域.[17]上述社区识别算法虽然对于识别社区都有一定的优势,但在种子选取策略和社区扩展策略上仍然存在问题.
1.2 CDCNCA算法简介
本文提出基于中心节点和社区吸引力的重叠社区识别算法(Overlapping Community Detection Algorithm Based on Central Node and Community Attraction,简称CDCNCA算法).在局部中心节点识别阶段,利用节点度数以及节点与相邻节点的区域内部连通性给出节点中心性系数,通过局部搜索找到中心节点,并作为社区扩展阶段的种子社区;在社区扩展阶段,考虑社区对一阶邻居节点的直接吸引力以及社区对二阶邻居节点的间接吸引力,以社区对这两类节点的吸引力作为节点归属社区的判断标准;最后,在不预设阈值的情况下,对重叠节点进行处理,使重叠节点识别更为准确,从而提高社区识别准确率.CDCNCA算法主要在3个方面有所创新:第一,利用节点度数和局部连通性建立局部中心节点评价模型,并通过局部搜索找到中心节点,将其作为社区扩展阶段的种子社区;第二,通过吸引力度量公式对社区的一阶邻居节点与二阶邻居节点是否能加入社区进行评判,弥补仅考虑一阶邻居节点的片面性,提高社区识别的准确率和效率;第三,在无需预先设置参数的情况下,对重叠节点作进一步分析处理,以完成社区识别任务.
2 CDCNCA算法
2.1 局部中心节点识别算法
通常,复杂网络表示为G=(V,E),其中V代表网络中节点个数为n的节点集合,E代表网络中连接个数为m的边集合.在复杂网络结构中,N(u)表示节点u的邻居节点集合,定义为:N(u)={v|(u,v)∈E,v∈V},节点度表示为D(u)=|N(u)|.
在复杂网络中,正确选取作为种子的中心节点对识别社区的准确度有直接影响.[18]因此,准确找到局部中心节点使其他节点在加入社区时更具目的性,也能快速加入社区,并且减少算法在社区扩展过程中的随机性.
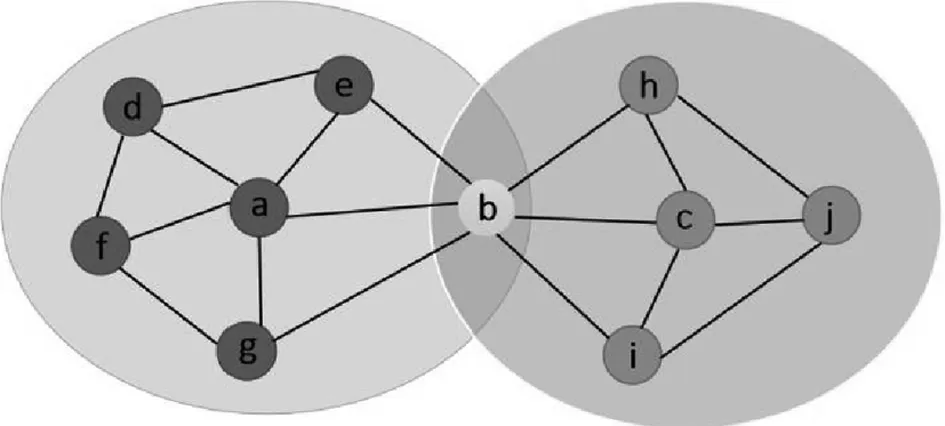
图1 复杂网络结构图
关于中心节点扩展的研究通常把节点度高的节点作为网络中心节点,未必适合在社区识别过程中应用.[19]因此,本算法同时考虑节点度以及节点与相邻节点的区域内部连通性这两个特性,以此提高局部中心节点的识别准确率.复杂网络结构图如图1所示,节点b的度为6,但它被两个社区共有,属于边界节点.虽然a、c的节点度分别只为5和4,但其与邻居节点之间连通性强并共同组成了一个连接稠密的小网络,有理由相信节点a、c可以作为局部中心节点.局部社区识别算法克服了只通过节点度数寻找局部中心节点的局限性.在给出局部中心节点识别算法前,先给出局部连通性和节点中心性系数的定义.
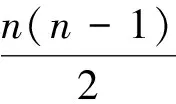
(1)
由定义1可知,在n固定的情况下,d越大,说明区域范围内节点连接越紧密,则节点x所在局部连通性越强,这符合社区结构中局部中心节点拥有高连通性的直观认识.
定义2(中心性系数)若节点x∈V、D(x)表示节点的度,则节点x的中心性系数可以表示为
(2)
可以看出,节点的中心性系数由节点度和表示局部连接紧密度的局部连通性共同决定,即从节点的个体角度与个体所在区域的角度共同分析节点在网络中的角色,局部中心节点识别算法如算法1所示.
算法1局部中心节点识别算法
输入网络G=(V,E)
输出局部中心节点集合S
1)begin
2)初始化集合S为空
3)whileV中未被访问的节点集合NV不为空
4) 从NV中随机选取一个节点node
5)cnode←根据公式(1)、(2)计算节点node的中心性系数
6)maxC=-1
7) whilecnode>maxC
8)maxC=cnode
9)Nnode←节点node的邻居节点集合
10) whileNnodei∈Nnode
11)C(Nnodei)←节点Nnodei的中心性系数
12) ifC(Nnodei)>cnode
13)cnode=C(Nnodei)
14)node=Nnodei
15) end if
16)Nnodei节点标记为已访问
17) end while
18)end while
19)S=S∪node
20)end while
21)end
在算法1中,第1~2行将中心节点集合初始化为空;第3~4行在网络中随机选取一个未被访问的节点;第5行计算随机选取节点的中心性系数;第7~19行将随机选取节点的中心性系数与其邻居节点的中心性系数进行比较,一直沿着该值增大的方向进行访问,直到所访问的区域内该节点的中心性系数最大,则此节点作为局部中心节点;第20行代表网络中的节点都已被访问,算法结束.
2.2 社区扩展算法
本社区识别算法为基于中心节点和社区吸引力的重叠社区识别算法.通过算法1找到复杂网络的局部中心节点,将其看作社区扩展过程中的种子社区,计算社区对节点的吸引力,并将其作为社区扩展的依据.本社区扩展算法不仅考虑社区对一阶邻居节点的吸引力,同时考虑社区对二阶邻居节点的吸引力,避免仅考量一阶邻居节点作为待加入节点的片面性,提高了社区识别的准确率.
定义3(社区-节点直接吸引力)设BC为社区扩展过程中的社区,节点v是社区BC的一阶邻居节点,社区BC对一阶邻居节点v的吸引力叫做直接吸引力,S(u,v)表示节点u和节点v的相似度,这里用Jaccard相似度求得;BCc、BCc+v分别表示节点v加入前与加入后的社区;m、m′表示节点v加入社区BC前后社区内部的边数.具体表示为
(3)
从直接吸引力函数可以看出,前半部分是节点v未加入到社区BC时,其社区内部节点间的平均相似度;后半部分是节点v加入到社区BC后,其社区内部节点间的平均相似度,其中差值代表被吸引节点对社区内部稠密程度影响的度量.直接吸引力大于0,则说明被吸引力节点对社区稠密度为正影响,可以将此节点加入到社区中,反之说明被吸引力节点会使社区内部稠密度降低,此节点不应该加到该社区中.
定义4(社区-节点间接吸引力)设BC为社区扩展过程中的社区,节点u是社区的二阶邻居节点,社区BC对二阶邻居节点u的吸引力叫做间接吸引力,具体表示为
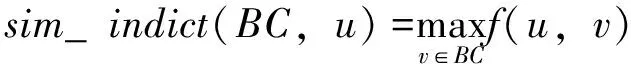
(4)
可以看出,社区对节点的间接吸引力表示为社区BC中的节点对节点u的吸引力最大值,现给出节点间的间接吸引力定义.
定义5(节点间的间接吸引力)设节点i,j∈V且满足N(i)∩N(j)≠∅、i∉N(j)、j∉N(i),因此,节点间的间接吸引力可定义为
(5)
由公式可知,公式前半部分为边相似度函数,用来计算节点i、j之间两条边的相似度,以此量化节点间的吸引力;边相似度越高,说明节点间的互相吸引力越大.公式的后半部分为节点i、j的公共邻居节点与去除节点i、j之外的其他相邻节点平均相似度的总和,其含义为对节点i、j产生的排斥力.例如,在现实社交网络中,拥有共同朋友的两个人具有相似爱好,但此共同朋友可能不止一个爱好,导致这两个人建立朋友关系时有其他阻碍.在给出上述定义后,社区扩展算法可表述为算法2.
算法2社区扩展算法
输入 局部中心节点集合CN,复杂网络G
输出 重叠社区结构C
1) begin
2) 初始化集合为空
3) whilec∈CN
4)BC←仅包含c的社区
5)n∈neighborNodes←社区的一阶邻居节点集合
6) while true
7) whilen∈neighborNodes
8)sim_dict(BC,n)←根据公式(3)计算BC对n的直接吸引力
9) end while
10)smax←sim_dict最大值
11) ifsmax>0
12)nmax←smax对应的一阶邻居节点
13)neighborNodes′←节点nmax的邻居节点集合
14)neighborNodes′←neighborNodes′-neighborNodes′∩BC
15) whilei∈neighborNodes′
16)sim_indict(BC,i)←根据公式(4)、(5)计算BC对i的间接吸引力
17) ifsim_indict(BC,i)>0
18) 将节点i加入到BC中
19) end if
20) end while
21) 将节点nmax加入到BC中
22) 更新BC的邻居节点集合neighborNodes
23) ifBC不再变化 break;
24) end if
25) end if
26) end while
27)C←C∪BC
28) end while
29)C←找到的社区结构
30)end
在算法2中,第1~2行是初始化集合;第7~9行是求社区对一阶邻居节点的直接吸引力值;第10~21行是得到直接吸引力最大值对应的一阶邻居节点和其相邻节点为社区二阶邻居节点的节点集合,计算社区对该类节点的间接吸引力值,将满足条件的一阶邻居节点与二阶邻居节点加入到社区中;第22行是执行一次操作后的社区邻居节点集合;第23~24行是判断社区结构是否变化,若不再变化则跳出循环并得到社区结果.
2.3 重叠节点分析
目前,众多重叠社区识别算法需要预设参数对重叠节点进行处理,但在网络信息无法掌握的情况下,设置阈值变得不太现实.因此,本文提出一种只需掌握重叠节点的点边信息就能准确识别重叠节点的分析方法,以此提高算法的普适性.
定义6(社区紧密度评价指标)设节点i为网络中的一个节点,社区C为已划分的社区,mc表示社区C内部拥有的边数,nc表示社区C内部拥有的节点数,则社区紧密度评价指标表示为
(6)
由上述定义可知,以社区内部边数量和社区内部点数量的比例作为评价指标,可以看出当社区紧密度评价指标越大时,社区内部节点连接越紧密.
定义7(社区紧密度增量)若节点i为一个重叠节点,CCc+i为重叠节点i加入社区C后的社区紧密度评价指标,CCc为重叠节点i未加入社区C后的社区紧密度评价指标.因此社区紧密度增量可以表示为
ΔCC=CCc+i-CCc
(7)
可以看出,当ΔCC>0时,重叠节点i加入社区C使得社区紧密度增大,反之社区紧密度减小.ΔCC越大,说明节点i加入社区C使社区内部节点越紧密.因此,通过社区紧密度增量可以判断重叠节点是否属于某社区.重叠节点分析算法如算法3所示.
算法3重叠节点分析算法
输入 已划分社区结构C={C1,C2,…,Cn},重叠节点集合O
输出 重叠节点分析后的社区结构
1) begin
2) for eacho∈O
3)OC←o所属的社区
4) for eachc∈OC
5) 根据公式(6)、(7)计算ΔCC
6) ifΔCC<0
7) 将节点o从社区c中删除
8) end if
9) end for
10) end for
11)end
2.4 CDCNCA算法
CDCNCA算法利用局部中心节点识别算法,得到网络中的局部中心节点集,使得局部中心节点组成的社区可以将周围节点快速吸引到社区中,确保算法快速收敛;在社区扩展阶段,以局部中心节点作为种子社区进行社区扩展,因为局部中心节点拥有较高的区域中心性,其范围内的节点在加入社区时更具目标性,从而减小社区扩展过程的随机性,增强社区结构的稳定性.另外,社区边界节点由于受到多个社区的吸引,容易成为重叠节点.为了提高社区识别的准确性,利用重叠节点分析算法对重叠节点进行处理,以社区紧密度增量为评价指标,精确识别重叠节点,从而找到网络的重叠社区结构.CDCNCA算法具体表述为算法4.
算法4CDCNCA算法
1) 通过局部中心节点识别算法得到局部中心节点集合S
2)S作为社区扩展算法的输入,输出网络社区结构C
3) 通过网络社区结构C得到重叠节点集合O
4) 社区结构C和重叠集合O为重叠节点分析算法的输入,输出处理完成的社区结构
5) 算法完成,返回最终社区划分
2.5 算法复杂度分析
设网络G共有n个节点、m条边,节点的平均度为k,社区的平均节点数为w,网络G的局部核心节点数为c,社区扩展过程发现的重叠节点数为o.在算法1寻找局部中心节点过程中,计算节点中心性系数c(x)所需的最坏时间复杂度为O(k(k-1)/2),每个节点与其邻居节点的中心性系数进行比较的时间复杂度为O(k),从而找到局部中心节点的时间复杂度为O((k(k-1)/2+k)),所以算法1的最坏时间复杂度为O(k2n).在进行社区扩展时,要判断由局部核心节点构成的社区对其一阶邻居节点和二阶邻居节点的作用力:在分析社区的一阶邻居节点时,最坏情况下所需时间为O(cwk);对于社区二阶邻居节点的判断,其最坏时间复杂度为O(cwk2).因此,社区扩展过程的时间复杂度为O(cwk+cwk2).在重叠节点分析过程中,需要考虑o个重叠节点的连接边,时间复杂度为O(ko),计算每个重叠节点的社区局部增量值,其最坏时间复杂度为O(ko).最终,本算法的时间复杂度为O(k2+k2n+cwk+cwk2+ko).由于在社区识别过程中,随着迭代次数的增加,节点数n会远大于k和w,因此算法时间复杂度可以表示为O(k2n).
进一步分析算法的空间复杂度可知,局部中心节点识别算法需要存储所有节点的中心性系数,所需空间为O(n);社区扩展阶段,需要存储社区对一阶邻居节点和二阶邻居节点的吸引力,其空间复杂度为O(cwk+cwk2);对重叠节点进行分析时,需要的空间为O(ko).由上可知,CDCNCA算法空间复杂度为O(n+cwk+cwk2+ko).因此,算法的空间复杂度为O(n).
3 实验分析
本节将给出算法在真实网络数据集和人工基准网络上的实验结果,并与经典算法CoEus[20]、SLPA[21]、EMOFM[22]、APAL[23]进行对比分析,以验证本算法的有效性,各对比算法的提出时间和开发环境如表1所示.实验运行环境是Intel Core i7-7500U 2.90GHz处理器,8GB内存,Windows 10操作系统.本文所提算法采用MATLAB R2021a编程.

表1 相关对比算法介绍
由于SLPA、APAL算法需要设置相关参数才能得到运行结果,因此,这些算法的参数设置如下:对于SLPA,将迭代次数T设置为100,过滤参数r设置为0.01到0.1,取值间隔为0.01;对于APAL,参数t设置为0.1到1,取值间隔为0.1.实验结果选取各参数下得到的最大值进行比较.
3.1 评价指标
为充分评价本算法的可行性,本文采用社区识别精度评价指标(NMI)[13]、社区连接紧密度评价指标(EQ)[24]两个评价指标.
3.2 实验方案
在采用本领域内经典的LFR-Benchmark人工基准网络生成器生成人工基准网络时,会同时给出网络真实社区结构.经典的社区识别精度评价指标NMI是通过比较算法识别的社区结构与网络真实社区结构之间的相似度来评价社区识别精度,从而在人工基准网络中运用NMI指标评价社区识别的精度.在真实网络中,已知真实社区结构的网络较少,无法进行算法识别社区结构与真实社区结构之间的精度比较,鉴于此,在真实网络中,本文采用了通用的评价社区内部节点连接紧密度的EQ指标来衡量算法的识别质量.
3.3 人工基准网络上的实验结果
本文采用的人工基准网络有以下参数:N表示网络中节点数量;kmax表示节点的最大度数;Cmax与Cmin分别代表社区中拥有的最大节点数和最小节点数;On表示网络中的重叠节点数量;Om表示重叠节点最多归属的社区数;μ是混合参数,用来控制社区结构,μ越小,则社区结构越明显.本文设计了4组不同类型的网络,具体如表2所示.

表2 人工基准网络参数设置
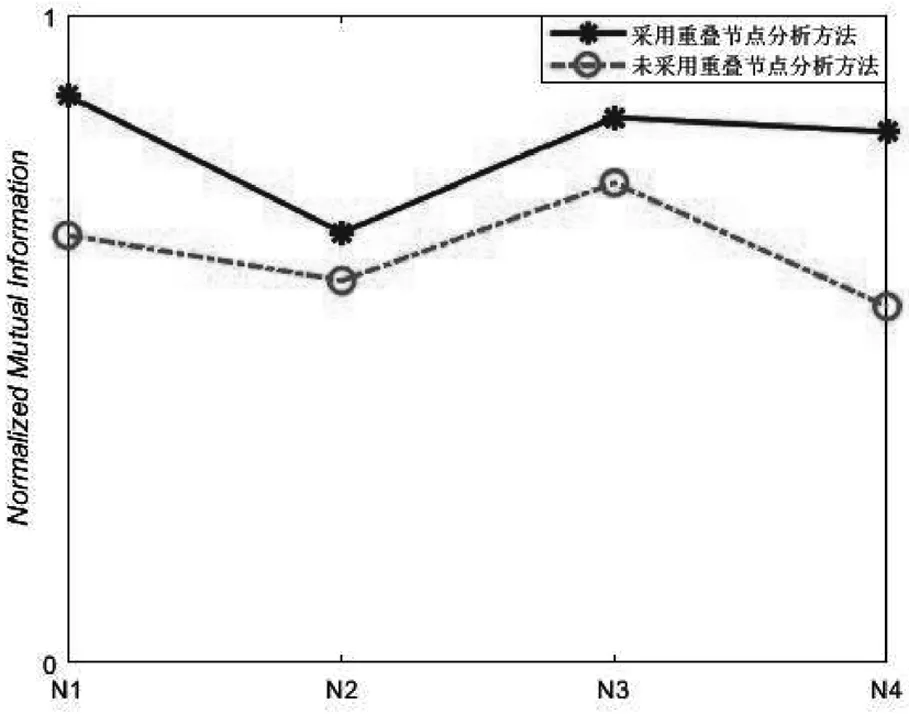
图2 针对重叠节点分析算法的消融实验结果
为验证重叠节点分析算法的有效性,将使用重叠节点分析算法的CDCNCA算法与未使用重叠节点分析算法的CDCNCA算法进行消融实验,采用上述人工基准网络,将N1和N2网络设置Om=3,N3和N4网络设置μ=0.1,实验结果如图2所示.
从图2可以看出,采用重叠节点分析算法的CDCNCA算法在4个人工基准网络上比未采用重叠节点分析算法的CDCNCA算法效果更好,取得了更高的NMI值,这是由于重叠节点分析算法从社区内部节点连接紧密度这一角度对重叠节点作进一步分析,以提高算法识别社区的准确率.
人工基准网络参数设置的不同,可以使得网络规模与复杂度具有一定区别,从而更好地验证各算法在不同网络的性能.图3给出了各算法在N1与N2网络中针对NMI评价指标的结果.
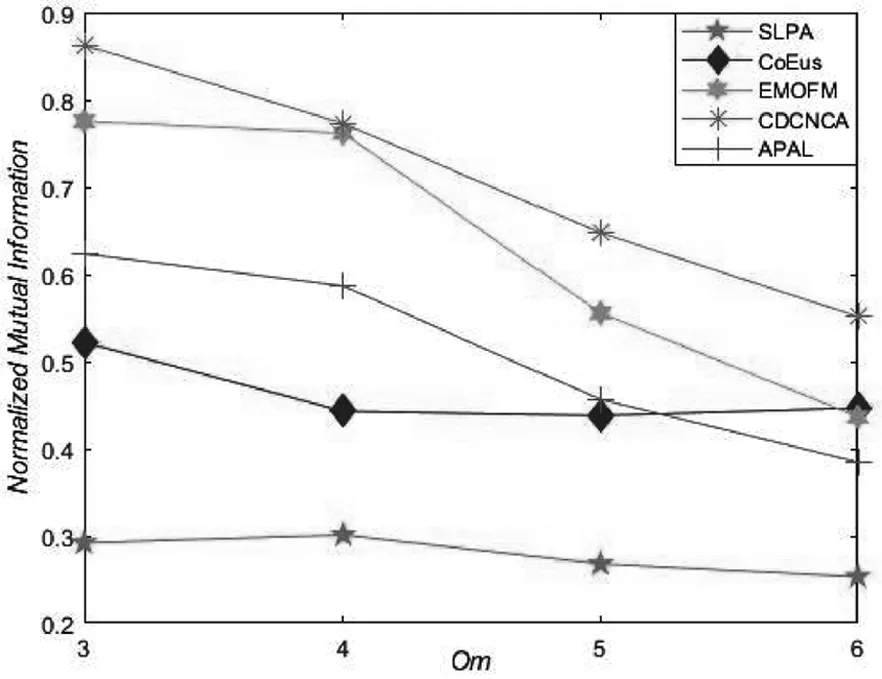
(a)N1
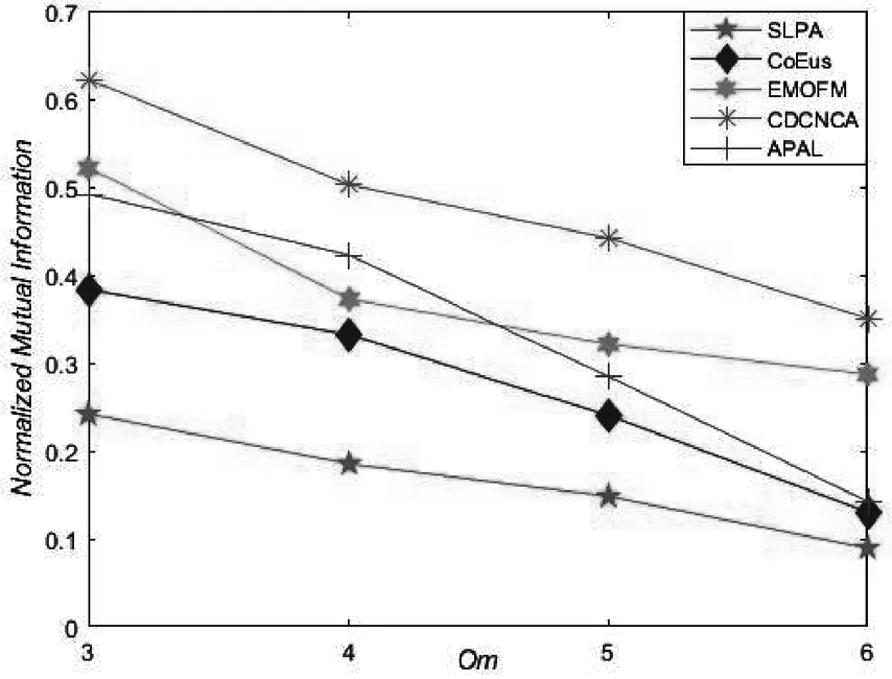
(b)N2
从图3可以看出,针对重叠度较低的N1网络,随着Om增加,CDCNCA算法、EMOFM算法和APAL算法的社区识别精度具有下降趋势,另外三种算法则趋于平稳.从总体上看,CDCNCA算法在Om=3~6的时候仍然取得最佳社区识别精度,SLPA算法由于随机选取节点作为初始节点,导致其随机性较强,故社区识别精度小于其他网络.在重叠节点较多的N2网络,5种算法的社区识别精度都随着Om的增大而逐渐减小,但CDCNCA算法的社区识别精度大于其他对比算法的社区识别精度.
图4给出了各算法在小规模网络N3和大规模网络N4中的社区识别精度对比结果.可以看出,各算法的社区识别精度大都随着μ增大而减小,这是因为随着μ增大,社区结构逐渐变得模糊,增加了社区识别的难度.在小规模网络N3中,当μ=0.2时,EMOFM算法的识别社区精度大于CDCNCA算法的社区识别精度,但在其他网络中,EMOFM算法求得的社区识别精度普遍小于CDCNCA算法的社区识别精度,这是由于EMOFM算法优化社区中心时仅考虑了节点度数,并不完全适用于所有网络,导致在其他网络识别的社区可能存在识别精度较低的问题.由此可以看出,CDCNCA算法在不同规模网络中相比于其他算法拥有较好的社区识别精度.
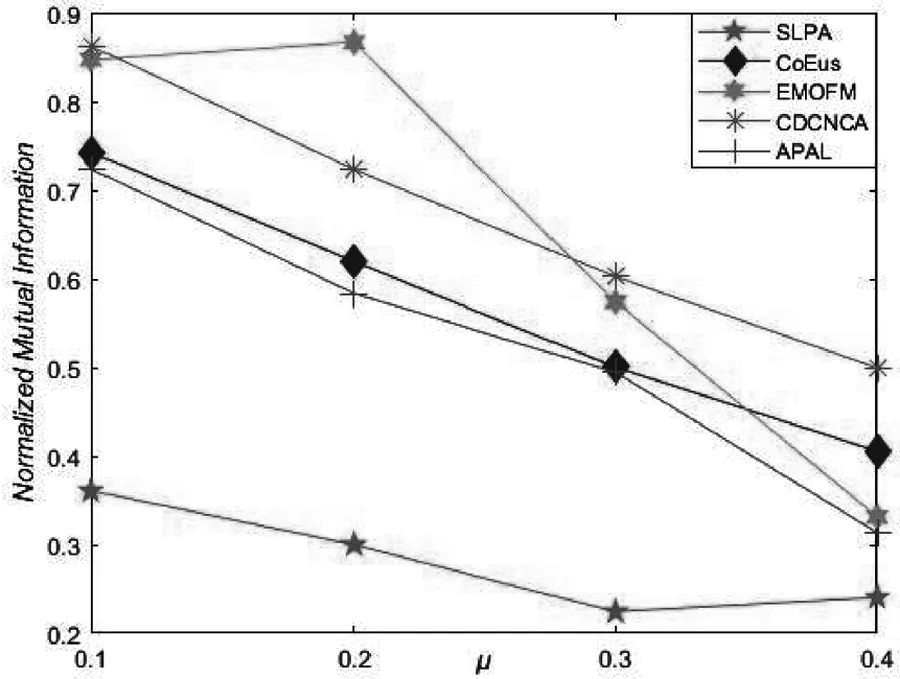
(a)N3

(b)N4
3.4 真实网络中的实验结果
社区识别算法的提出是为了将其应用到真实网络中,虽然已在人工基准网络上验证了算法的有效性和可行性,但还需要进一步验证其在真实网络中的性能.由于在真实网络数据集中已知的真实社区结构较少,并且都是非重叠社区,无法较好地对算法进行全面的检验,故采用EQ评价指标来检验社区内部节点的连接紧密度.本节运用表3中的真实网络数据集来验证各算法的社区连接紧密度.

表3 真实网络数据集
表4给出了CDCNCA算法与其他算法针对7个真实网络数据集求得的EQ值(“~”表示算法无法求出社区结构或者EQ值趋近于0).从表4可知,CDCNCA在Karate、Dolphins、Polbooks、Polblogs、Internet网络中EQ值最高,在Email真实网络中取得的EQ值为第二,在Email网络中小于EMOFM算法,在PGP网络中EQ值小于SLPA算法和EMOFM算法,这是由于EMOFM算法在这两个网络中选取了较准确的中心节点.另外,SLPA算法在相对稀疏的PGP网络中识别出规模较小的网络,从而社区内部节点连接紧密度较高.综上可知,CDCNCA对于真实网络中的社区结构具有较强的识别能力,对于不同规模的网络都具有一定的稳定性.这是由于CDCNCA算法采用了质量较高的中心性系数识别中心节点作为种子,因此,所识别社区的社区连接紧密度较高.

表4 各算法的EQ值
4 结语
CDCNCA算法通过中心性系数评价指标找到网络中的局部中心节点,使网络中其他节点在加入社区时更具目的性,从而提高社区识别的准确率,加快了算法的收敛速度;而将局部中心节点作为种子社区,充分考虑了网络结构对社区形成过程的影响,以社区对一阶邻居节点和二阶邻居节点的吸引力作为加入社区的判断标准,从而找到了重叠社区;对重叠节点的处理方法无需设置阈值,既能提高对重叠社区的识别精度,又可提高算法的普适性.CDCNCA算法仅需掌握复杂网络点边结构信息,无需获取先验知识便可找到重叠社区结构.
在人工基准网络数据集中,通过对社区识别精度分析可知,随着重叠节点归属数Om增大,CDCNCA算法较为稳定并且社区识别精度整体大于其他算法;随着μ值的增大,NMI评价值逐渐减小,与其他对比算法相比,CDCNCA算法在社区识别精度方面有较大优势.这是由于CDCNCA算法在局部中心节点选取时,同时考虑了局部连通性和节点度,并且相比其他算法,本算法在社区扩展时另外考虑了社区对二阶邻居节点的吸引力,使得算法充分利用网络结构信息.另外,在7个真实网络数据集中,除了PGP网络数据集和Email网络数据集,CDCNCA算法在EQ指标上未取得最大值,在其他5个网络中得到了对比算法中的最佳值.通过对不同规模网络的划分结果可知,CDCNCA算法可以合理地识别社区结构.因此,在人工基准网络和真实网络中,CDCNCA算法都表现出了良好的性能,从而验证了本算法的可行性、有效性.
